Модуль числа
реклама
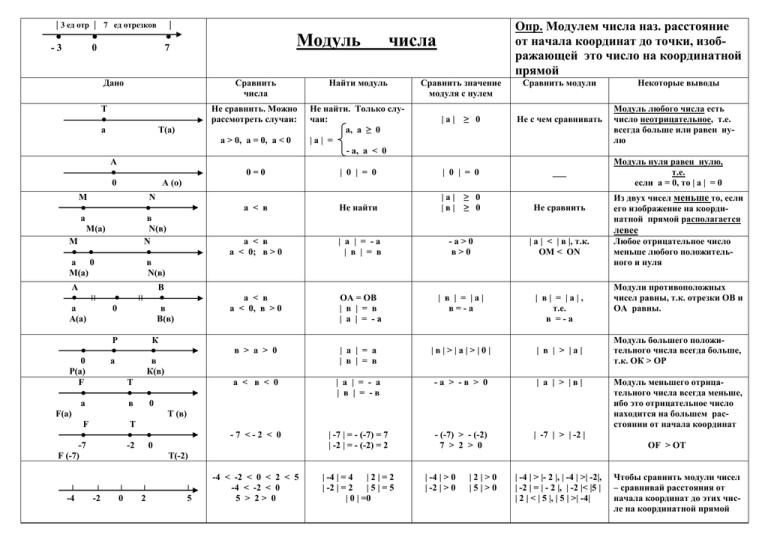
| 3 ед отр | 7 ед отрезков | ● ● ● -3 0 7 Модуль Дано Т ● а Найти модуль Не сравнить. Можно рассмотреть случаи: Не найти. Только случаи: а, а ≥ 0 |а| = - а, а < 0 а > 0, а = 0, а < 0 А ● 0 N ● в N(в) N ● в N(в) М ● ● а 0 М(а) ׀ -4 ● 0 Сравнить модули |а| ≥ 0 Не с чем сравнивать 0=0 | 0 | = 0 | 0 | = 0 ___ а < в Не найти |а| ≥ 0 |в| ≥ 0 Не сравнить а < в а < 0; в > 0 | а | = -а | в | = в -а>0 в>0 | а | < | в |, т.к. ОМ < ОN а < в а < 0, в > 0 ОА = ОВ | в | = в | а | = -а | в | = |а| в=-а | в| = |а|, т.е. в =-а в > а > 0 | а | = а | в | = в |в|>|а|>|0| | в | > |а| К ● в К(в) T ● в а < в < 0 | а | = - а | в | = -в -а > -в > 0 | а | > |в| -7 <-2 < 0 | -7 | = - (-7) = 7 | -2 | = - (-2) = 2 - (-7) > - (-2) 7 > 2 > 0 | -7 | > | -2 | ● 0 Т (в) T ● -2 Некоторые выводы Модуль любого числа есть число неотрицательное, т.е. всегда больше или равен нулю Модуль нуля равен нулю, т.е. если а = 0, то | а | = 0 Из двух чисел меньше то, если его изображение на координатной прямой располагается левее В ● в В(в) ׀׀ Р ● а ● 0 Р(а) F ● а F(а) F ● -7 F (-7) Сравнить значение модуля с нулем А (о) М ● а М(а) А ● ׀׀ а А(а) числа Сравнить числа Т(а) Опр. Модулем числа наз. расстояние от начала координат до точки, изображающей это число на координатной прямой ● 0 Любое отрицательное число меньше любого положительного и нуля Модули противоположных чисел равны, т.к. отрезки ОВ и ОА равны. Модуль большего положительного числа всегда больше, т.к. ОК > ОР Модуль меньшего отрицательного числа всегда меньше, ибо это отрицательное число находится на большем расстоянии от начала координат OF > OT T(-2) ׀ -2 ׀ 0 ׀ 2 ׀ 5 -4 < -2 < 0 < 2 < 5 -4 < -2 < 0 5 > 2> 0 | -4 | = 4 |2|=2 | -2 | = 2 |5|=5 | 0 | =0 | -4 | > 0 | -2 | > 0 |2|>0 |5|>0 | -4 | > |- 2 |, | -4 | >| -2|, | -2 | = | - 2 |, | -2 |< |5 | | 2 | < | 5 |, | 5 | >| -4| Чтобы сравнить модули чисел – сравнивай расстояния от начала координат до этих числе на координатной прямой











