Математическое моделирование для выявления степени влияния на развитие экономики. Х
реклама
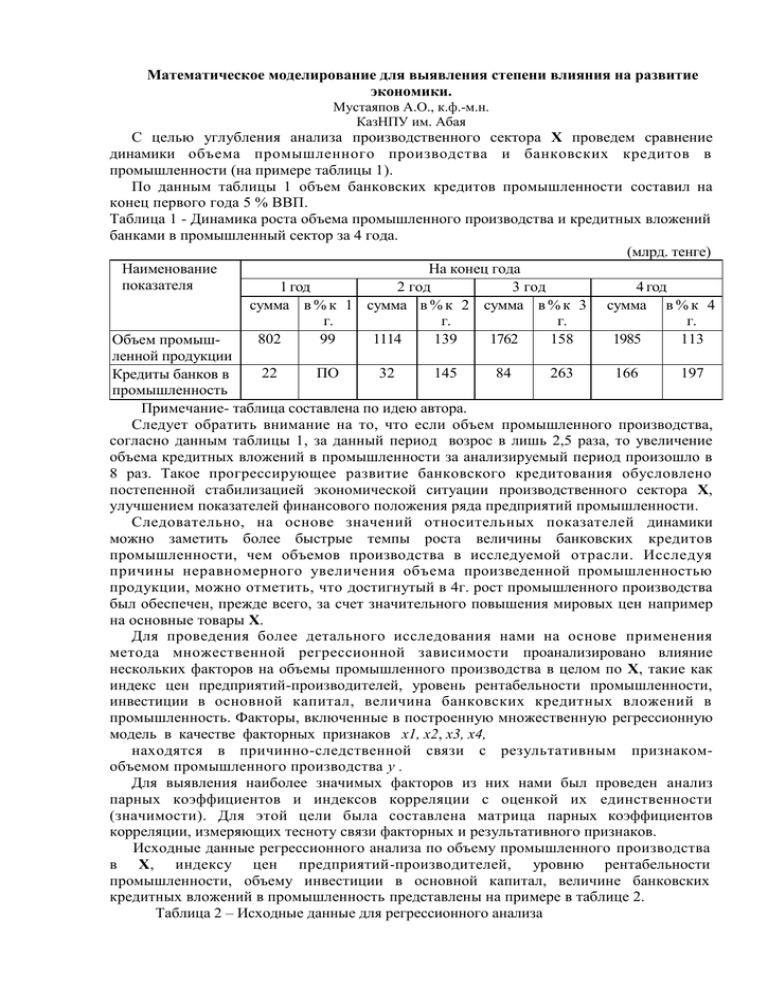
Математическое моделирование для выявления степени влияния на развитие экономики. Мустаяпов А.О., к.ф.-м.н. КазНПУ им. Абая С целью углубления анализа производственного сектора Х проведем сравнение динамики объема промышленного производства и банковских кредитов в промышленности (на примере таблицы 1). По данным таблицы 1 объем банковских кредитов промышленности составил на конец первого года 5 % ВВП. Таблица 1 - Динамика роста объема промышленного производства и кредитных вложений банками в промышленный сектор за 4 года. (млрд. тенге) Наименование На конец года показателя 1 год 2 год 3 год 4 год сумма в % к 1 сумма в % к 2 сумма в % к 3 сумма в % к 4 г. г. г. г. 802 99 1114 139 1762 158 1985 113 Объем промышленной продукции 22 ПО 32 145 84 263 166 197 Кредиты банков в промышленность Примечание- таблица составлена по идею автора. Следует обратить внимание на то, что если объем промышленного производства, согласно данным таблицы 1, за данный период возрос в лишь 2,5 раза, то увеличение объема кредитных вложений в промышленности за анализируемый период произошло в 8 раз. Такое прогрессирующее развитие банковского кредитования обусловлено постепенной стабилизацией экономической ситуации производственного сектора Х, улучшением показателей финансового положения ряда предприятий промышленности. Следовательно, на основе значений относительных показателей динамики можно заметить более быстрые темпы роста величины банковских кредитов промышленности, чем объемов производства в исследуемой отрасли. Исследуя причины неравномерного увеличения объема произведенной промышленностью продукции, можно отметить, что достигнутый в 4г. рост промышленного производства был обеспечен, прежде всего, за счет значительного повышения мировых цен например на основные товары Х. Для проведения более детального исследования нами на основе применения метода множественной регрессионной зависимости проанализировано влияние нескольких факторов на объемы промышленного производства в целом по Х, такие как индекс цен предприятий-производителей, уровень рентабельности промышленности, инвестиции в основной капитал, величина банковских кредитных вложений в промышленность. Факторы, включенные в построенную множественную регрессионную модель в качестве факторных признаков x1, x2, x3, x4, находятся в причинно-следственной связи с результативным признакомобъемом промышленного производства у . Для выявления наиболее значимых факторов из них нами был проведен анализ парных коэффициентов и индексов корреляции с оценкой их единственности (значимости). Для этой цели была составлена матрица парных коэффициентов корреляции, измеряющих тесноту связи факторных и результативного признаков. Исходные данные регрессионного анализа по объему промышленного производства в Х, индексу цен предприятий-производителей, уровню рентабельности промышленности, объему инвестиции в основной капитал, величине банковских кредитных вложений в промышленность представлены на примере в таблице 2. Таблица 2 – Исходные данные для регрессионного анализа Показатели Объем промышленного производства, млрд. тенге(yi) Индекс цен предприятийпроизводителей, в % к предыдущему году (Xi) Уровень рентабельности промышленности, в % (х2) Инвестиции в основной капитал, млрд. тенге (x3) Сумма кредитных вложений банков в промышленность, млрд. тенге(х4) 1год 2год 3год 4год 5год 6год 810 802 1114 1762 1985 2292 239,8 100,8 115,5 118,8 100,3 111,9 5,3 5,9 15,8 26,5 20,0 22 85,0 157,6 219,6 385,9 550,6 1193,1 20 22 32 84 166 235,4 П р и м е ч а н и е - Примечание- таблица составлена по идею автора. Для определения тесноты связи между этими факторами были рассчитана матрица парных коэффициентов корреляции, результаты которой представлены в таблице 3. Таблица 3 - Матрица парных коэффициентов корреляции VAR1 VAR2 VAR3 VAR4 VAR5 VAR1 1,00 -,48 ,87 ,88 ,94 VAR2 -,48 1,00 -,52 -,40 -.40 VAR3 ,87 --52 1,00 ,62 ,66 VAR4 ,88 -,40 ,62 1.00 ,96 VAR5 ,94 -,40 ,66 ,96 1,00 Анализ матрицы парных коэффициентов корреляции показал, что факторный признак х1 (VAR2) может быть исключен из модели, так как парные коэффициенты корреляции свидетельствуют о наличии слабой связи (-,48; -,52; -,40; -,40). На основе результатов вычислений парных коэффициентов корреляции и использовании программы «Информационная технология линейной регрессии» [1] были получены значения показателей дисперсионного и регрессионного анализа, представленные в таблице 4. Факторная дисперсия результативного признака, составившая 681013,5, намного превышает значение остаточной дисперсии результативного признака, равной 672,9 (на примере таблицы 4). Это значит, что согласно результатам дисперсионного анализа основная часть вариации величины промышленного производства Х зависит от воздействия исследуемых факторов, влияние остальных факторов незначительно. Таблица 4 – Дисперсия результативного признака Регрессионная статистика Множественный R 0,999671 R-квадрат 0,999342 Нормированный R-квадрат 0,998354 Стандартная ошибка 25,94214 Наблюдения 6 Дисперсионный анализ df SS MS F Значимость F Регрессия 3 2043041 681013,5 1011,915 0,000987 Остаток 2 1345,99 672,9948 Итого 5 2044387 В свою очередь, коэффициент детерминации, рассчитанный как отношение факторной дисперсии к общей дисперсии, составил 0,99 или 99 % (коэффициент детерминации представлен как R-квадрат). Значит, факторы, включенные в уравнение регрессии объясняют 99 % вариации величины промышленного производства, если рассматривать значение анализируемых показателей за 6 лет. Правомерность модели подтверждается значением F-критерия Фишера [1]. Практический F - критерий Фишера составил 20 и оказался больше F теоретического (по таблице значений F-критерий Фишера при уровне значимости 0,05), который равен t(l;10)=4,96. Это значит, что построенная модель регрессии будем считать правомерна. Изученная с помощью корреляционного метода статистическая связь между исследуемыми показателями свидетельствует о целесообразности построения следующей регрессионной модели (уравнения): Уx = a +b1x1 + b2x2 + b3X3, (1) где свободный член уравнения а = 529 ,92; коэффициенты условно-чистой регрессии b1 = 32 ,7 , b 2 = 0 , 3 1 ; b3 = 5,99; Следовательно, формульная зависимость может быть представлена в следующем виде: ух = 529 ,92 + 32 ,7 Х1 - 0.31 Х2 + 5.99 Хз (2) Рассматривая значимость каждого фактора в отдельности, следует отметить, что все исследуемые факторы оказывают определенное влияние на объем промышленного производства Х. Это подтверждается значениями коэффициентов корреляции. По индексу цен предприятий-производителей он составил 0,23 (слабая связь несущественное влияние на увеличение объемов промышленного производства); по уровню рентабельности промышленности - 0,76 (тесная связь - существенное влияние); объему инвестиций в основной капитал - 0,90 (очень тесная связь существенное влияние); по объему банковских кредитов в промышленность - 0,88 (очень тесная связь - существенное влияние). b. x Согласно коэффициенту эластичности, рассчитываемому как Э у y , увеличение суммы кредитных вложений банков в промышленность на 1 % при прочих равных условиях приведет к увеличению объема промышленного производства на 0,52 %. Регрессионную зависимость у от х4 можно представить графически в виде диаграммы (рисунок 1). Кривая на рисунке 1 показывает зависимость объема промышленного производства от размера кредитных вложений банков второго уровня Казахстана в промышленность по данным за период 1-6гг. Прямая на рисунке 1 отражает линию оцененного по этим данным уравнения парной регрессии (линия тренда). Таким образом, на основе проведенного регрессионного анализа можно сделать следующие выводы. Фактор X (величина кредитов банков второго уровня в промышленность), включенный в уравнение регрессии объясняет 88 % вариации величины промышленного производства, если рассматривать значение показателей за период 1-6гг. Это значит, что изменение суммы банковских кредитов при прочих равных условиях оказывает существенное влияние на изменение объема промышленного производства. Уравнение полученной регрессии можно использовать для прогноза участия кредитов банковской системы в развитии промышленности Х на будущее. 2,500 2,292 млрд. тенге 2,000 1,762 1,500 1,114 1,000 500 0 1,985 810 802 20 22 84 32 166 235 период Y X Рисунок 1 – Зависимость объема промышленного производства от величины банковских кредитов в промышленность Кривая на рисунке 1 показывает зависимость объема промышленного производства от размера кредитных вложений банков второго уровня Казахстана в промышленность по данным за период 1-6гг. На основе проведенного регрессионного анализа можно сделать следующие выводы. Фактор X (величина кредитов банков второго уровня в промышленность), включенный в уравнение регрессии объясняет 88 % вариации величины промышленного производства, если рассматривать значение показателей за период 1-6гг. Это значит, что изменение суммы банковских кредитов при прочих равных условиях оказывает существенное влияние на изменение объема промышленного производства. СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 1. Копбаев Г.Ш., Ергенбекова Н.С. Стратегическое планирование в банке: основные аспекты // Банки Казахстана. №3 – 2001. с. – 1518. 2. Поморина М.А. Планирование как основа управления деятельности банка – М.: Финансы и статистика, 2002. – 384 с. 3. Спицын И.О., Спицын Я.О. Маркетинг в банке. – Тернополь: АО Тарнекс, 1997. – 257 с. 4. Аханов С. Банковская система в условиях глобализации: стратегический подход // Саясат №2 – 2004. – с. 7074. 5. Копабаева Г.Ш., Ергебекова Н.С. Стратегическое планирование в банке: основные аспекты. // Банки Казахстана -№3 –2001. – с. –15-18.
