Основы теории правл._практика

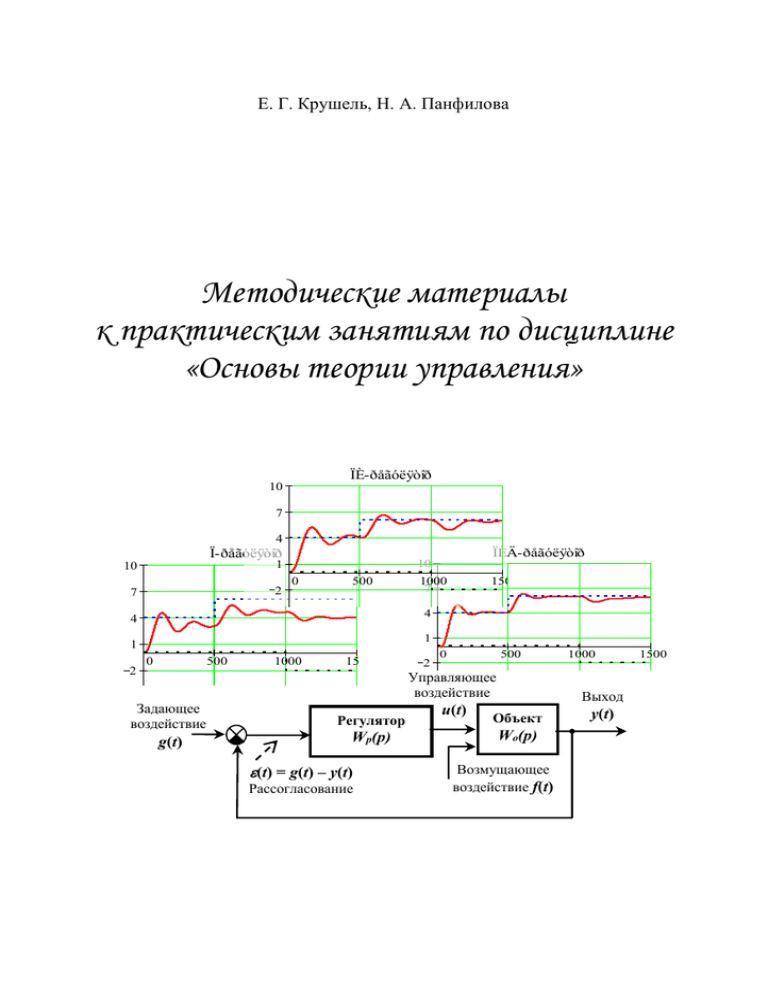
Е. Г. Крушель, Н. А. Панфилова
Методические материалы
к практическим занятиям по дисциплине
«Основы теории управления»
ÏÈ-ðåãóëÿòîð
10
7
4
ÏÈÄ-ðåãóëÿòîð
Ï-ðåãóëÿòîð
10
1
7
2
4
5
10
0
500
1500
4
1
1
2
1000
7
0
500
1000
1500
2
0
500
Управляющее
5
воздействие
5
Задающее
воздействие
Регулятор
g(t)
Wp(p)
(t) = g(t) – y(t)
Рассогласование
u(t)
1000
Выход
Объект
Wо(p)
Возмущающее
воздействие f(t)
y(t)
1500
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
КАМЫШИНСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ (ФИЛИАЛ)
ГОУ ВПО «ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Е. Г. Крушель, Н. А. Панфилова
Методические материалы
к практическим занятиям по дисциплине
«Основы теории управления»
Учебное пособие
Волгоград
2010
УДК 658.012.011.56(075.8)
К 84
Рецензенты: академик РАЕН, член-корр. Международной академии
наук РФ, д. ф.-м. н., профессор Саратовского государственного технического университета В. Б. Байбурин; д. т. н., профессор Самарского государственного аэрокосмического университета им. академика С. П. Королёва В. Л. Балакин
Крушель, Е. Г. МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ К ПРАКТИЧЕСКИМ ЗАНЯ«ОСНОВЫ ТЕОРИИ УПРАВЛЕНИЯ»: учеб. пособие /
Е. Г. Крушель, Н. А. Панфилова; ВолгГТУ, Волгоград, 2010. – 136 с.
ТИЯМ ПО ДИСЦИПЛИНЕ
ISBN 978-5-9948-0564-0
Предназначено для студентов и преподавателей технических вузов,
осуществляющих подготовку бакалавров по направлению «Информатика
и вычислительная техника» и по близким направлениям.
Область использования – практические занятия по дисциплине «Основы теории управления», подготавливающие студентов к инженерной,
прикладной деятельности в сфере автоматического управления технологическими объектами. Может быть полезно как студентам, ориентирующимся на практическую деятельность в будущем, так и преподавателям,
перед которыми стоит задача повысить мотивацию студентов к изучению
теории.
Ил. 100. Табл. 1. Библиогр.: 8 назв.
Печатается по решению редакционно-издательского совета
Волгоградского государственного технического университета
ISBN 978-5-9948-0564-0
©
Волгоградский
государственный
технический
университет, 2010
ПРЕДИСЛОВИЕ
Дисциплина «Основы теории управления», включенная в учебные
планы большинства направлений подготовки бакалавров техники и технологии, располагает в настоящее время мощными средствами научной и
методической поддержки. Поэтому, уважаемый Читатель, в предисловии
мы должны дать пояснения, на основе которых Вы сможете решить, пригодится ли Вам наша книга как дополнение к опубликованным ранее и
общедоступным учебникам – например, [1...5]. Эти пояснения касаются
трех вопросов: первый – зачем (с какой целью) написано учебное пособие; второй – как (с какой позиции) в пособии излагается материал; третий – что (какая тематика) в нем содержится.
Вначале поясним цель написания пособия. Мы адресуем его студентам и преподавателям технических вузов и их филиалов, осуществляющих подготовку бакалавров по направлению «Информатика и вычислительная техника» и по близким направлениям. Как показывает многолетний опыт преподавания в одном из таких вузов (Камышинский технологический институт (филиал) Волгоградского государственного технического университета), дисциплина «Основы теории управления», практически не имеющая дисциплин-предшественников ни в средней школе, ни
в учебной программе младших курсов вуза, воспринимается студентами с
большим трудом.
Блестящий трехтомник «Методы классической и современной теории автоматического управления», созданный коллективом авторов
МГТУ им. Н. Э. Баумана под редакцией заслуженного деятеля науки РФ,
д. т. н., профессора Н. Д. Егупова [1], является прекрасной базой для
обучения студентов машиностроительных и приборостроительных специальностей вузов-флагманов, ведущих подготовку студентов к научной
работе и к руководству инновационными проектами в будущем.
К сожалению, уровень сложности представленного в [1] материала
превышает резервы преподавания основ теории управления, предусмотренные образовательным стандартом подготовки бакалавров. В частности, для направления «Информатика и вычислительная техника» в учебном плане на изучение дисциплины «Основы теории управления» отводится всего 119 часов, в том числе 68 часов аудиторных занятий. В таких
условиях перед преподавателем стоит сложная проблема выбора соотношения между объемами знаний, предоставляемых в лекционном курсе
(34 часа), в сопровождающих практических (18 часов) и лабораторных
(16 часов) занятиях, а также в материалах, которые студенты должны
освоить самостоятельно (51 час, в том числе 17 часов для выполнения
семестрового задания).
3
Нужно учесть, что изучение теоретических основ наукоёмких дисциплин, к числу которых относится дисциплина «Основы теории управления», не имеет у некоторых учащихся технических вузов достаточной
мотивации из-за прагматичности студентов бакалавриата, осознающих,
что большинство выпускников будет занято в сфере эксплуатации и, возможно, в сферах наладки и усовершенствования действующих систем
управления (но не в сферах науки, проектирования и преподавания).
Понимая это, мы решили отказаться от обычной схемы проведения
практических занятий в форме разбора примеров и иллюстраций к теоретическому курсу (эти примеры включены в семестровое задание, выполняемое студентами самостоятельно; источником примеров служат классический учебник [2] и очень хорошо составленный сборник задач [3]).
Вместо этого мы попытались разработать тематику и методику практических занятий, подготавливающих студентов к инженерной, прикладной деятельности в сфере автоматического управления технологическими объектами. В результате в преподавании дисциплины «Основы теории
управления» оказалось возможным реализовать две параллельные линии:
основы теории управления (лекции и семестровое задание) и основы инженерной практики управления (практические и лабораторные занятия),
причем нужно отметить, что именно благодаря практическим аспектам у
многих студентов возникает интерес и к теоретическим проблемам
управления.
Наш опыт преподавания основ теории управления по такой схеме
показал, что можно представить учебно-методические материалы по
каждой из данных линий в форме автономных пособий. Предлагаемое
Вашему вниманию пособие содержит учебный материал, относящийся
именно ко второй, инженерной, линии преподавания дисциплины.
Таким образом, в ответ на возможный вопрос Читателя о цели написания пособия авторы ответили бы так: они надеются на то, что изложенный в нем практический материал будет способствовать привитию студентам знаний и выработке у них некоторых навыков в области инженерных приложений теории управления. Можно также надеяться на повышение интереса студентов к теории управления как одной из важнейших дисциплин, формирующих специалиста в области кибернетики, информационных технологий и автоматизированных систем. Материалы
могут принести пользу как студентам, ориентирующимся на практическую деятельность в будущем, так и преподавателям, перед которыми стоит задача повысить мотивацию студентов к изучению теории (и которые,
возможно, согласятся с методикой изучения основ теории управления, используемой нами).
Следующий вопрос, который нуждается в пояснении, относится к
позиции авторов, принятой для изложения практических аспектов
4
управления. Возможны два альтернативных подхода к преподаванию основ теории управления.
Согласно первому подходу система управления в технике рассматривается как воплощение идеи, сформулированной первоначально в математической форме. Этот подход приводит к изложению основ теории
управления на языке прикладной математики. Пример описания одного
из свойств системы управления с этой позиции: «Данная система неустойчива, потому что некоторые корни ее характеристического уравнения имеют положительную вещественную часть».
Согласно второму подходу принципы управления рассматриваются
как результат переноса физических закономерностей в мир техники. Этот
подход приводит к трактовке теории управления как самостоятельной
отрасли естественных наук, использующей математику как удобный
язык. Пример описания того же явления с этой позиции: «Данная система
управления неустойчива, поскольку ее инерционные элементы сдвигают
фазу выхода по отношению к фазе входного воздействия настолько сильно, что время, в течение которого система действует в условиях положительной обратной связи, превышает время, в течение которого обратная
связь отрицательна».
Можно проследить результат наличия этих двух подходов при рассмотрении научно-технической литературы по теории управления. С одной стороны – мощная теоретическая база, в которой эксплуатируются
(и почти автономно сосуществуют) практически все разделы прикладной
математики; сфера научных публикаций – массовая в связи с широкими
перспективами новизны; сфера внедрения – узкая, чаще всего ограничивается единичными, но высокоэффективными экспериментальными системами. С другой стороны – инженерные методы расчета регуляторов с
весьма ограниченным составом алгоритмов, изобретенных по аналогии с
механизмами регулирования в природе; математическая база – упрощенная; сфера публикаций ограничена в связи с отсутствием новизны; сфера
внедрения – массовая.
Авторы понимают, что каждый из подходов имеет стройную аргументацию, которую они не берутся ни принять полностью, ни отвергнуть
полностью. Но наш опыт преподавания показывает, что в обычном техническом вузе, большинство студентов которого редко проявляет склонность к математике, изложение практических аспектов управления на основе второго («физического») подхода воспринимается легче, поскольку
имеется возможность обратиться к здравому смыслу и аналогиям. Именно этот подход (в отличие от большинства учебных пособий) мы и приняли при описании центральных тем пособия, посвященных структуре
систем с обратной связью и регуляторам (как линейным, так и нелинейным).
5
Дополнительным аргументом в пользу выбора «физического» подхода является возможность проиллюстрировать логику инженерного
мышления (и, как мы надеемся, содействовать формированию такого
мышления), рассматривающего задачу по схеме: от конечной цели – через процедуру анализа причин, препятствующих ее достижению, – к
нахождению (часто – изобретению нового) способа ее достижения. Эта
схема, принятая в пособии при описании линейных и нелинейных законов управления, создает в студенческой аудитории обстановку, в которой
известные алгоритмы воспринимаются не как данность, а как результат
собственного «изобретения».
Перейдем к аннотированному описанию содержания пособия, представленного восемью темами; затраты учебного времени – 18 аудиторных
часов и 18 часов (из 51 часа, предусмотренного учебным планом) самостоятельной работы.
Тема 1 «Этапы работ при создании систем автоматического
управления (САУ)», для изучения которой отводится 2 часа аудиторных
и 2 часа самостоятельных занятий, знакомит студентов с базовым составом работ, которые должен выполнить инженер, разрабатывающий систему управления объектом:
1. Анализ структуры объекта управления: определение технологической цели его функционирования, выявление управляющих воздействий
и возмущений, определение состава переменных состояния и выходов
объекта.
2. Изучение принципов работы объекта: определение физических
законов, на основе которых действует объект, и технологических ограничений, накладываемых на его работу.
3. Экспериментальное исследование объекта управления и составление его математической модели, ориентированной не столько на отражение принципов работы объекта, сколько на решение задачи выбора
структуры и параметров системы автоматического управления.
4. Выбор структуры системы управления.
5. Разработка алгоритмов управления и контроля (измерения) выхода объекта и переменных состояния.
6. Разработка программного и технического обеспечения.
7. Определение настроечных параметров алгоритмов управления и
контроля.
8. Моделирование работы автоматизированного технологического
комплекса и уточнение настроечных параметров алгоритмов.
9. Наладка САУ на реальном объекте, определение реальных показателей качества управления и (при необходимости) корректировка решений по п. 3…8.
6
Последующие практические занятия посвящены детальному рассмотрению позиций 3...7.
Тема 2 «Сглаживание экспериментальных зависимостей. Оценка
параметров модели объекта», для изучения которой отводится 2 часа
аудиторных и 2 часа самостоятельных занятий, посвящена двум методам
(скользящего среднего и четвертых разностей), используемым для обработки кривых разгона, искаженных помехами. Приводятся сведения об
области применения каждого метода и об их настройке. Описывается
процедура идентификации параметров статической и динамической модели.
Тема 3 «Построение передаточных функций. Понятие об управлении с обратной связью», для изучения которой отводится 2 часа аудиторных и 2 часа самостоятельных занятий, знакомит студентов с различными способами представления математической модели объекта, ориентированной на выбор структуры и алгоритмического обеспечения системы автоматического управления. Выявляются особенности замкнутой
системы управления и поясняется (на содержательном, «физическом»
уровне) роль обратной связи (регулятора) как для подавления возмущений (внешних и внутренних, параметрических), так и для ускорения динамических процессов в системах управления различного целевого назначения (в системах автоматической стабилизации, программного управления и
следящих системах).
Тема 4 «Структурные преобразования САУ с перекрестными
связями», для изучения которой отводится 2 часа аудиторных и 2 часа
самостоятельных занятий, посвящена подробному разбору примера, иллюстрирующего технологию структурных преобразований многосвязной
системы для получения общей передаточной функции САУ по каналам:
«задающее воздействие – выход объекта»; «задающее воздействие – рассогласование между заданием и выходом объекта»; «возмущающее воздействие – выход объекта»; «возмущающее воздействие – рассогласование между заданием и выходом объекта».
Темы 5 – 7 «Линейные законы управления», рассчитанные на 6
часов аудиторных и 6 часов самостоятельных занятий, являются центральными темами пособия. Изложение построено таким образом, чтобы
вовлечь студентов в процесс «изобретения» законов управления. Рассмотрение известных линейных законов (пропорционального (П-), интегрального (И-), пропорционально-интегрального (ПИ-), пропорциональноинтегрально-дифференциального (ПИД-)) начинается с простейшего Пзакона. Анализируются свойства систем управления с П-регулятором.
Выявляются достоинства и причины недостатков этих систем, в результате чего обосновывается естественный переход к более сложным линейным законам. Для каждого из законов проводится исследование свойств
7
(устойчивости и качества) систем управления различного целевого
назначения (стабилизации, слежения, программного управления) как при
воспроизведении задающих воздействий, так и при подавлении внешних
и параметрических возмущений.
Тема 8 «Нелинейные законы управления», рассчитанная на 4 часа
аудиторных и 4 часа самостоятельных занятий, дает представление о
функциональных, логических, оптимизационных и параметрических законах. Используется методический прием, позволяющий студентам
участвовать в «изобретении» функциональных нелинейных законов
управления на основе анализа недостатков линейных законов. Раздел темы «Оптимизирующие нелинейные законы управления» дает представление (к сожалению, из-за ограничения учебного времени, очень краткое
и поверхностное) об огромном и увлекательном мире синтеза алгоритмов.
К пособию прилагается компакт-диск с демонстрационными материалами (презентации, выполненные в среде Microsoft Office PowerPoint),
которые могут быть использованы для проведения занятий в аудиториях,
оборудованных компьютерной проекционной аппаратурой. Поскольку
большинство технических вузов сталкивается с проблемой недостаточности опыта у преподавателей, которым поручается проведение практических занятий, мы посчитали целесообразным снабдить некоторые слайды
заметками, включающими как советы по методике изложения отдельных
позиций пособия, так и примеры из личного опыта авторов по разработке
систем управления.
Возможно предоставление компьютерного и методического сопровождения как к практическим занятиям, так и к лабораторным работам,
тематика которых связана с материалами, изучаемыми на практических
занятиях. Заявки принимаются по адресу [email protected].
8
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1
ТЕМА: «ЭТАПЫ РАБОТ ПРИ СОЗДАНИИ САУ»
Время проведения практического занятия (аудиторные часы) – 2 часа.
Время самостоятельной работы студента (дополнительные часы) – 2 часа.
Цель занятия: ознакомиться с базовым составом работ, которые
должен выполнить инженер, разрабатывающий систему управления объектом.
Рассматриваемые вопросы:
1. Базовый состав работ для создания САУ.
2. Рассмотрение иллюстративного примера (система управления
нагревательной установкой).
3. Первичные понятия о методах экспериментального исследования
объектов управления.
1. Основные работы, выполнение которых необходимо для создания
эффективной САУ
Общее число этапов – 9. Приведем их перечень:
1. Определение структуры объекта управления (рис. 1.1).
Структура объекта
управления
Технологическая цель
функционирования
объекта
Входы
Возмущающие
факторы
Измеряемые
Выходы
Управляющие
факторы
Неизмеряемые
Переменные
состояния
Измеряемые
Недоступные
для измерения
Рис. 1.1. Структура объекта управления
2. Изучение физических основ технологии работы объекта:
а) определение физических законов, на основе которых действует объект;
б) определение технологических ограничений на работу объекта.
Этапы 1 и 2 находятся вне теории автоматического управления.
3. Экспериментальное исследование объекта управления и составление его математической модели, ориентированной не столько
на отражение физических основ работы объекта, сколько на ре9
4.
5.
6.
7.
8.
9.
шение задачи выбора структуры и параметров системы автоматического управления.
Выбор структуры системы управления. Наиболее часто используемые альтернативы:
а) управление по отклонению (с обратной связью);
б) управление с компенсацией возмущений;
в) комбинированные системы, сочетающие оба принципа.
Разработка алгоритмов управления и контроля (измерения) выхода объекта и переменных состояния.
Разработка программного и технического обеспечения.
Определение настроечных параметров алгоритмов управления и
контроля.
Моделирование работы автоматизированного технологического
комплекса (объекта управления + системы управления) и уточнение настроечных параметров алгоритмов.
Наладка САУ на реальном объекте, определение реальных показателей качества управления и (при необходимости) корректировка решений по этапам 3 – 8 или 4 – 8.
Мнемоническая запись фаз работы по созданию САУ приведена на
рис. 1.2 (этапы, входящие в круг задач дисциплины «Основы теории
управления», выделены заливкой):
Обратные связи от этапа
внедрения к пересмотру
решений, принятых на
предшествующих этапах
разработки
Этап 2
Этап 3
Этап 4
Этап 5
Этап 6
Этап 7
Проектирование САУ
Этап 1
Этап 8
Этап 9
Внедрение САУ
Рис. 1.2. Фазы работы по созданию САУ
2. Пример: система управления нагревательной установкой
Объектом управления является виртуальный объект, имитирующий котельную, которая работает на угле. Автоматизируемым процессом является процесс нагрева.
10
Схема экспериментальной установки показана на рис. 1.3.
1 – бункер с углем; 2 – тарельчатый питатель; 3 – нож; 4 – транспортер топлива;
5 – печь котельной; 6 – воздуходувка; 7 – подача охлажденного воздуха;
8 – электродвигатель постоянного тока.
Рис. 1.3. Схема виртуального объекта управления
Технологической целью работы установки является обеспечение заданной температуры в условиях, когда работа установки подвержена действию возмущающих факторов. Источником возмущающих воздействий
является холодный воздух, подаваемый в печь с помощью воздуходувки.
Описание принципа работы виртуального объекта. Подача угля в
топку печи осуществляется по транспортеру (рис. 1.3). Топливо попадает
на транспортер с вращающейся тарелки питателя; расход топлива зависит
от скорости вращения тарелки и от положения ножа, отсекающего уголь
с тарелки на транспортер. Регулирование расхода топлива осуществляется электродвигателем постоянного тока, вал которого соединен с валом
тарельчатого питателя. Управление скоростью вращения двигателя (а через нее – скоростью вращения тарелки и, следовательно, подачей топлива
в печь) осуществляется путем изменения магнитного потока обмотки
возбуждения двигателя. Последовательно с обмоткой включен ряд сопротивлений, значения которых установлены согласно двоичному коду,
т. е. равны 1 Ом, 2 Ома, 4 Ома, …, 128 Ом (здесь и далее числовые значения условны: приведены только для примера). Диапазон возможных значений общего сопротивления в цепи обмотки возбуждения составляет
0…255 Ом. Значению 255 Ом соответствует минимальная температура
11
Tmin в печи (равна температуре окружающей среды, Tmin = 20 C). Значению 0 Ом соответствует максимально достижимая температура
Tmax = 1000 C. Любые из секций общего сопротивления могут быть закорочены, благодаря чему в цепи обмотки возбуждения можно установить произвольное целое значение сопротивления из диапазона 0…255
Ом. Например, на рис. 1.3 установлено общее сопротивление (27 + 25 +
+ 24 + 21 + 20) = 179 Ом.
Путем изменения положения ножа тарельчатого питателя можно изменять расход топлива на транспортер при одной и той же скорости вращения тарелки. Нож питателя предполагается неподвижным.
Влияние внешней среды, приводящей к отклонению температуры от
постоянного значения, имитируется подачей холодного воздуха, осуществляемой воздуходувкой.
Описание системы управления установкой. Измерения текущих
значений температуры в печи, сопровождаемые измерительными помехами (рис. 1.3), поступают в систему управления, работа которой состоит
в подборе такого значения суммарного сопротивления, чтобы температура в печи соответствовала заданной.
Особенности объекта с позиций теории управления: управляющее воздействие (расход топлива) подается в печь с запаздыванием, связанным с перемещением материала по транспортеру. Процесс нагрева является инерционным: мгновенное изменение температуры при изменении
расхода топлива невозможно. В системе управления используются результаты измерения температуры, искаженные помехами.
3. Необходимые теоретические сведения
3.1. Понятие о кривых разгона и переходных функциях
Представим себе, что печь включается в работу с состояния, когда
температура в ней равна температуре окружающей среды, а напряжение,
питающее обмотку возбуждения электродвигателя, поступает через максимально возможное значение суммарного сопротивления R = Rmax = 255
Ом. Поскольку установка спроектирована так, что при R = Rmax температура в печи минимальна, изменений температуры не будет (она останется
равной температуре окружающей среды).
Теперь представим себе, что печь по-прежнему включается в работу
с состояния, когда температура в ней равна температуре окружающей
среды, но напряжение, питающее обмотку возбуждения электродвигателя, поступает через значение суммарного сопротивления, меньшее, чем
максимально возможное: R = 205 Ом < Rmax. Начнется процесс нагрева, и
через некоторое время в печи установится новое значение температуры
(например, 196 С).
12
Пусть в момент времени, который условно обозначен нулевым (t = 0,
рис. 1.4), было произведено скачкообразное (т. е. мгновенное) уменьшение
сопротивления с 205 Ом до 155 Ом. Произойдет постепенный разогрев
печи (рис. 1.4). Если фиксировать значения температуры в печи, то получим график изменения температуры во времени, который содержит следующие фрагменты:
 Начальная часть: несмотря на то, что сопротивление уменьшилось, изменения температуры не наблюдаются (либо из-за недостаточной чувствительности измерительного прибора, либо из-за
наличия тракта передачи тепла от места его ввода до места измерения).
Определение: период времени от момента скачкообразного изменения входного воздействия (сопротивления) до момента начала
фиксации изменений выходного сигнала (температуры) называется запаздыванием.
 Срединная часть: измерительный прибор фиксирует наличие
изменений выходного сигнала (температуры), несмотря на то, что
входное воздействие (сопротивление) не изменяется. Эти изменения объясняются наличием инерционности («памяти») объекта. В
тепловых объектах эта память объясняется тем, что порции нагретого воздуха в печи смешиваются с остальным воздухом, «помнящим» прежнюю температуру.
Определение: период времени, началом которого является момент начала фиксации измерительным прибором изменений выходного сигнала, а окончанием – момент, начиная с которого показания измерительного прибора перестают изменяться, называется периодом инерционности.
 Концевая часть: измерительный прибор показывает, что выходной сигнал (температура) перестает изменяться, т. е. достигнуто
новое установившееся значение выходного сигнала.
Определение: режим, при котором при постоянных входных воздействиях выходной сигнал объекта длительное время остается
постоянным, называется статическим (установившимся) режимом.
13
Рис. 1.4. Кривая разгона и ее элементы
Внимательно рассмотрите рис. 1.4, определите участки запаздывания, инерционности, старого и нового статического режимов.
Определение: если снять экспериментально зависимость выходного
сигнала от времени, вызванную скачкообразным изменением входного
воздействия (измеряя значения выхода в равноотстоящие моменты времени небольшой продолжительности), то получим кривую, называемую
кривой разгона.
Кривая разгона, полученная экспериментально, обычно отличается
от идеализированной кривой (рис. 1.4) тем, что эксперимент неизбежно
сопровождается измерительными помехами и изменениями, вызванными дрейфом (медленным неизбежным изменением) параметров объекта (рис. 1.5).
14
Рис. 1.5. Экспериментальная кривая разгона. Выход объекта измерен с помехами
Эти факторы ставят перед экспериментатором противоречивые задачи: с одной стороны, для устранения помех желательно снять несколько
кривых разгона и затем их усреднить. Но такой опыт неизбежно будет
длительным, и в течение опыта параметры объекта успеют измениться,
что нарушит воспроизводимость опыта. Поэтому, с другой стороны, опыт
не должен быть слишком продолжительным.
В связи с этим обычно проводят одно- или двукратное снятие кривой
разгона и затем сглаживают результаты каким-либо методом.
Для чего нужно сглаживать экспериментальные кривые? Наличие помех затрудняет подбор уравнений, описывающих объект (т. е. составление его математической модели). Поэтому первым этапом обработки кривых разгона является их сглаживание, цель которого заключается в «вычленении» идеальной кривой разгона (такой, как показана на
рис. 1.4) из реальной (такой, как показана на рис. 1.5). Для сглаживания
используются различные методы. На практическом занятии №2 будут
рассмотрены два из них: метод скользящего среднего и метод четвертых разностей (иначе – метод парабол).
15
3.2. Примеры математических моделей процесса нагрева
Для того чтобы получить математическую модель какого-либо объекта, всегда необходимо иметь в качестве гипотезы перечень возможных моделей (такой список формируется на базе прошлых исследований аналогичных объектов, результаты которых публикуются в научной литературе).
Процессы, непрерывные во времени, обладающие свойствами инерционности и наличием запаздывания, чаще всего описываются в терминах линейных дифференциальных уравнений. Рассмотрим четыре простейших (и наиболее употребительных в инженерной практике) модели:
1. Модель в форме дифференциального уравнения 1-го порядка без
запаздывания (в теории управления такая модель называется
«апериодическое звено первого порядка»).
2. Модель в форме дифференциального уравнения 1-го порядка с
запаздыванием (в теории управления структура такой модели
представляется последовательным соединением апериодического
звена первого порядка и звена запаздывания).
3. Модель в форме дифференциального уравнения 2-го порядка без
запаздывания, характеристические числа действительные (в теории управления такая модель называется «апериодическое звено
второго порядка»).
4. Модель в форме дифференциального уравнения 2-го порядка с
запаздыванием (в теории управления структура такой модели
представляется последовательным соединением апериодического
звена второго порядка и звена запаздывания).
Приведем формальное описание этих моделей.
3.2.1. Модель в форме дифференциального уравнения 1-го порядка
без запаздывания (апериодическое звено первого порядка):
dx(t )
(1.1)
T0 
 x(t )  k 0  u (t ) ,
dt
где x(t) – выход модели (скаляр), в интерпретации примера (рис. 1.3) –
сигнал, имитирующий температуру в печи, C;
u(t) – один из входов объекта (скаляр), в интерпретации примера (рис.
1.3) – либо управляющее воздействие (общее сопротивление, включенное
последовательно с обмоткой возбуждения двигателя, Ом), либо возмущающее воздействие (расход охлаждающего воздуха, м3/с);
T0 – постоянная времени модели, физическая размерность [T0] = c, этот
параметр характеризует инерционность процесса нагрева. На рис. 1.6 показано сравнение двух моделей (1.1) с разными постоянными времени.
Мы видим, что статический режим достигается тем позже, чем больше
постоянная времени. Имеется полезная инженерная оценка: установив16
шийся режим с достаточной для практики точностью достигается
спустя промежуток времени, равный утроенной постоянной времени: 3T0;
k0 – коэффициент усиления модели, показывает, на какую величину изменится выход объекта в установившемся режиме, если вход изменится
на единицу по сравнению со значением, при котором имела место «старая» статика. Физическая размерность коэффициента усиления для раз размерность выхода 
личных объектов разная: [k 0 ]  
 , в рассматривае размерность входа 
о
мом примере [k ]   С  .
0
 Ом 


Рис. 1.6. Сравнение двух апериодических звеньев первого порядка без запаздывания
На рис. 1.7 показано сравнение двух моделей (1.1) с одинаковыми
постоянными времени и разными коэффициентами усиления, входные
воздействия для обеих моделей одинаковы. Мы видим, что установившийся режим для этих моделей различен: при меньшем коэффициенте
усиления достигается меньшее значение выхода. Зная величину входа и
коэффициент усиления, можно рассчитать установившееся значение
выхода объекта.
Рис. 1.7. Сравнение двух апериодических звеньев первого порядка с различными
коэффициентами усиления
17
Расчет приращения (по отношению к значению в «старой» статике)
выхода объекта по (1.1) как реакции на входное воздействие, изменяюu , t  0
щееся скачком при t = 0 ( u (t )   1
) (при условии, что до момента
u2 , t  0
времени t = 0 имел место статический режим, «старая» статика), производится по формуле:
t



T0
x(t )  k0  1  e




,
  u2  u1 

(1.2)
где Δx(t) = x(t) – x(0);
x(0) – значение выхода объекта в режиме «старой» статики.
Применимость простейшей модели (1.1) зависит от соотношения
между запаздыванием и инерционностью объекта (рис. 1.8). Если запаздывание невелико по сравнению с периодом достижения статического
режима, то модель (1.1) применима (рис. 1.8а). При увеличении запаздывания точность модели быстро ухудшается (рис. 1.8б).
а) если запаздывание невелико (по сравнению с
инерционностью объекта) и если процесс в
объекте начинается с высокой скоростью (не
плавно), то аппроксимация простейшей моделью 1-го порядка без запаздывания вполне
пригодна
б) если в объекте запаздывание существенно, то аппроксимация моделью первого порядка без запаздывания не удовлетворительна
Рис. 1.8. Иллюстрация к условиям применимости модели 1-го порядка без запаздывания
3.2.2. Модель в форме дифференциального уравнения 1-го порядка с
запаздыванием (последовательное соединение звеньев: апериодическое
звено первого порядка и звено запаздывания):
dx(t )
(1.3)
T0 
 x(t )  k 0  u (t   ) ,
dt
где  – время запаздывания, физическая размерность [] = с; остальные
обозначения такие же, как в формуле (1.1).
18
На рис. 1.9 показано влияние запаздывания на вид процесса, описываемого моделью (1.3); коэффициенты усиления и постоянные времени
для обоих процессов, показанных на рисунке, одинаковы. Мы видим, что
наиболее существенны различия в начальной стадии процесса; с течением времени эти различия уменьшаются, и статический режим в обоих
случаях одинаков.
Рис. 1.9. Модели 1-го порядка с различными запаздываниями
Расчет приращения (по отношению к значению в «старой» статике)
выхода объекта по (1.3) как реакции на входное воздействие, изменяю-
u1 , t  0
) (при условии, что до момента
u2 , t  0
щееся скачком при t = 0 ( u (t )  
времени t = 0 имел место статический режим, «старая» статика), производится по формуле:
0,
t 

(t  ) 
 

x(t )   

,
(1.4)
k 0  1  e T0   u 2  u1 , t  
 


 
где Δx(t) = x(t) – x(0);
x(0) – значение выхода объекта в режиме «старой» статики.
Область применимости модели (1.3), естественно, шире, чем модели
(1.1), поскольку величина запаздывания учитывается непосредственно.
Успех применения (1.3) зависит от того, насколько гладкой является
начальная часть динамического процесса в объекте (рис. 1.10). Если процесс начинается «резво», т. е. производная в момент t = τ быстро возрастает, то модель (1.3) имеет хорошую точность (рис. 1.10а). При гладком
начале динамического процесса точность модели ухудшается (рис. 1.10б).
19
Нормированный (приведенный
к диапазону 0...1)
выход модели и объекта
Модель
Модель
Кривая разгона объекта
Кривая разгона объекта
а) если процесс в объекте начинается с высокой скоростью, не гладко, то аппроксимация
моделью первого порядка с запаздыванием
вполне пригодна
б) если начальная часть процесса в объекте гладкая, то аппроксимация моделью первого порядка с запаздыванием
теряет точность
Рис. 1.10. Иллюстрация к условиям применимости модели 1-го порядка с запаздыванием
3.2.3. Модель в форме дифференциального уравнения 2-го порядка с
действительными характеристическими числами (апериодическое звено
2-го порядка). Для того чтобы гарантировать отсутствие комплексно сопряженных характеристических чисел, дифференциальное уравнение задается в специальной форме:
d 2 x(t )
dx(t )
(1.5)
T1  T2 
 (T1  T2 ) 
 x(t )  k 0  u (t ) ,
2
dt
dt
где T1 и T2 – две постоянные времени модели, размерность [T1] = [T2] = с,
T1 ≠ T2 (без ограничения общности будем обозначать постоянные времени так, что T1 > T2);
остальные обозначения такие же, как в формуле (1.3).
Пояснение: характеристические числа рассчитываются по уравнению:
T1  T2  2  (T1  T2 )    1  0 ,
отсюда
1, 2 


 (T1  T2 )  (T1  T2 ) 2  4  T1  T2

2  T1  T1
 (T1  T2 )  T12  T22  2  T1  T2  4  T1  T2

2  T1  T1
 (T1  T2 )  T12  T22  2  T1  T2  (T1  T2 )  (T1  T2 ) 2


2  T1  T1
2  T1  T1

 (T1  T2 )  (T1  T2 )
,
2  T1  T1
20
1  
1
;
T1
2  
1 .
T2
(1.6)
Значения характеристических чисел получились действительными.
Они порождают два переходных процесса в форме экспонент с постоянными времени T1 и T2.
Общая инерционность (т. е. время, необходимое для перехода от
«старой» к «новой» статике) определяется суммой постоянных времени, а
степень гладкости начального участка переходного процесса – соотношением между ними. Мы видим (рис. 1.11), что при существенно различных постоянных времени начальная часть процесса менее гладкая, чем
при близких значениях.
Рис. 1.11. Чем более близки значения Т1 и Т2, тем более гладкой является начальная часть
процесса в апериодической модели 2-го порядка без запаздывания
Расчет приращения (по отношению к значению в «старой» статике)
выхода объекта по (1.5) как реакции на входное воздействие, изменяюu1 , t  0
щееся скачком при t = 0 ( u (t )  
) (при условии, что до момента
u2 , t  0
времени t = 0 имел место статический режим, «старая» статика), производится по формуле:
t
t


 

1
(1.7)
x(t )  k0  1 
  T1  e T1  T2  e T2   u2  u1  ,

 T1  T2 

где Δx(t) = x(t) – x(0);
x(0) – значение выхода объекта в режиме «старой» статики.
Как и при использовании модели (1.1), применимость модели (1.5)
зависит (рис. 1.12) от соотношения между запаздыванием и инерционностью объекта. Если запаздывание невелико по сравнению с периодом достижения статического режима, то модель (1.5) применима (рис. 1.12а).
Область применимости модели (1.5) шире, чем модели (1.1), т. к.
гладкий участок начальной части процесса в (1.5) может имитировать запаздывание (в модели (1.1) такой участок отсутствует).
21
Температура, °С
Температура, °С
Модель
Кривая разгона объекта
а) если запаздывание невелико (по сравнению с инерционностью объекта), то аппроксимация моделью 2-го порядка без запаздывания пригодна (гладкая начальная
часть процесса в модели имитирует запаздывание в объекте)
Модель
Кривая разгона объекта
б) если запаздывание в объекте существенно, модель 2-го порядка без запаздывания теряет точность
Рис. 1.12. Иллюстрация к условиям применимости модели 2-го порядка без запаздывания с
действительными характеристическими числами
3.2.4. Модель в форме дифференциального уравнения 2-го порядка с
запаздыванием и с действительными характеристическими числами (последовательное соединение апериодического звена 2-го порядка и звена
запаздывания). Дифференциальное уравнение имеет форму, аналогичную (1.5), но в него введено запаздывание  аналогично (1.3):
d 2 x(t )
dx(t )
(1.8)
T1  T2 
 (T1  T2 ) 
 x(t )  k0  u (t   ) .
dt 2
dt
Расчет приращения (по отношению к значению в «старой» статике)
выхода объекта по (1.8) как реакции на входное воздействие, изменяюu1 , t  0
щееся скачком при t = 0 ( u (t )  
) (при условии, что до момента
u2 , t  0
времени t = 0 имел место статический режим, «старая» статика), производится по формуле:
0,
t 

(t  )
(t  ) 





, (1.9)
1
x(t )  
T1

k  1
 (T1  e
 T2  e T2 )  u 2  u1 , t  
 0  T1  T2





где Δx(t) = x(t) – x(0);
x(0) – значение выхода объекта в режиме «старой» статики.
Область применимости модели (1.8) шире, чем модели (1.5), т. к.
участок переходного процесса, соответствующий запаздыванию, гладко
(т. е. без разрыва производной по времени dx(t ) ) сопрягается с участdt
t 
ком x(t), t > τ. Благодаря этому удается представить моделью (1.8) динамические процессы с большими запаздываниями (рис. 1.13).
22
Рис. 1.13. Иллюстрация высокого качества представления динамики объекта с большим
запаздыванием моделью 2-го порядка с запаздыванием
3.2.5. Мы видим (рис. 1.13), что даже модель 2-го порядка с запаздыванием не всегда позволяет достичь совпадения в начальной части переходного процесса: модель сначала опережает процесс в объекте, а затем
отстает от процесса. Если по результатам экспериментальных исследований получилось заметное расхождение, можно попытаться усложнить
модель – в частности, путем использования модели в форме дифференциального уравнения 3-го порядка (без запаздывания, как (1.1), или с запаздыванием, получаемым из (1.1) аналогично (1.8)) с действительными характеристическими числами:
T1  T2  T3 
d 3 x(t )
d 2 x(t )
dx(t )
 (T1  T2  T1  T3  T2  T3 ) 
 (T1  T2  T3 ) 

3
dt
dt
dt 2
 k  u (t ), без запаздывания
(1.10)
 x(t )   0
k0  u (t   ), с запаздыванием
Расчет приращения (по отношению к значению в «старой» статике)
выхода объекта по этой модели как реакции на входное воздействие, изu1 , t  0
меняющееся скачком при t = 0 ( u (t )  
) (при условии, что до моu2 , t  0
мента времени t = 0 имел место статический режим, «старая» статика),
производится по формуле:
0,
t 



( t  )
( t  )


 
T12
T22
k 0  1 
 e T1 
 e T2 
x(t )  
(T2  T1 )  (T2  T3 )
 (T1  T2 )  (T1  T3 )
 
( t  )



T32
t 

 e T3   (u 2  u1 ),
(T3  T1 )  (T3  T1 )




где Δx(t) = x(t) – x(0);
x(0) – значение выхода объекта в режиме «старой» статики.
23
(1.11)
3.3. Общие рекомендации о применении математических моделей
3.3.1. О целесообразности использования как можно более простых
моделей. Сравним модели (1.1), (1.3), (1.5), (1.8) и (1.10). Мы видим, что
по мере возрастания сложности модели возрастает и число параметров,
которые нужно определить по экспериментальным данным. Поэтому
чем сложнее модель, выбранная нами, тем более продолжительным должен быть эксперимент на объекте. На практике продолжительные эксперименты нежелательны по двум причинам:
1. Позиция Заказчика работы: всякий эксперимент связан с нарушениями номинальных условий работы объекта; продолжительные нарушения вызывают технологические нарушения и экономические потери, рассматриваемые производственниками как
крайне нежелательные.
2. Позиция разработчика системы управления: при длительном
эксперименте могут сказаться изменения параметров объекта
(явление дрейфа, см. рис. 1.5); в результате эксперимент потеряет
воспроизводимость.
Поэтому из всех моделей, обеспечивающих достаточную точность
воспроизведения динамики объекта, следует выбирать простейшую.
3.3.2. Поскольку результаты эксперимента практически всегда искажаются помехами (рис. 1.5), «маскирующими» свойства объекта, необходимым этапом составления математической модели объекта является
устранение помех (соответствующие методы рассматриваются на практическом занятии № 2).
4. Контрольные вопросы
Перечислите основные этапы, выполнение которых необходимо
для создания эффективной САУ.
2. Какова технологическая цель функционирования объекта, рассматриваемого на практическом занятии в качестве примера?
3. Что является возмущающим воздействием в примере, рассматриваемом на практическом занятии? Что является управляющим
воздействием? Что является выходом объекта?
4. Что такое запаздывание?
5. Что такое период инерционности?
6. Что такое статический (установившийся) режим?
7. Что такое кривая разгона, зачем она используется, как ее получить?
8. Для чего нужно сглаживать экспериментальные кривые?
9. Приведите примеры математических моделей процесса нагрева.
10. Что показывает коэффициент усиления модели объекта?
1.
24
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 2
ТЕМА: «СГЛАЖИВАНИЕ ЭКСПЕРИМЕНТАЛЬНЫХ
ЗАВИСИМОСТЕЙ. ОЦЕНКА ПАРАМЕТРОВ МОДЕЛИ ОБЪЕКТА»
Время проведения практического занятия (аудиторные часы) – 2 часа.
Время самостоятельной работы студента (дополнительные часы) – 2 часа.
Цель занятия: ознакомиться с назначением и методами обработки
экспериментальных данных и с методикой определения параметров модели объекта по кривым разгона.
Рассматриваемые вопросы:
1. Цель обработки экспериментальных данных (на примере кривых
разгона).
2. Метод скользящего среднего.
3. Метод четвертых разностей.
4. Сравнение методов и определение областей их применения.
5. Методика оценки параметров модели первого порядка с запаздыванием.
В качестве примера используются результаты экспериментального
исследования нагревательного объекта (см. описание практического занятия № 1).
1. Цель обработки экспериментальных данных
Рассмотрим типичный пример экспериментальной кривой разгона
(рис. 1.5). Если попытаться подобрать модель, выход которой будет воспроизводить экспериментальную кривую разгона, то такая модель отразит не только свойства объекта, но и свойства измерительных помех:
внутренние характеристики объекта окажутся «замаскированными»
внешними помехами.
Поэтому экспериментальную зависимость подвергают предварительной обработке с целью сгладить ее и выявить зависимость, порожденную свойствами самого объекта.
Примечание: глагол «сгладить» имеет тот же корень, что и «глаз»: в зрение встроен
весьма совершенный механизм сглаживания, с помощью которого мы без труда видим зависимость, «замаскированную» помехами; в этом легко убедиться, если прорисовать зависимость, подлежащую выявлению, по рис. 1.5.
Итак, цель обработки экспериментальных данных (в частности, экспериментальных кривых разгона) состоит в выявлении зависимостей, порожденных свойствами объекта (эти зависимости в экспериментальных
данных «замаскированы» помехами).
25
Понятно, что механизм подавления помех базируется на усреднении
(негласно предполагается, что помехи имеют нулевое среднее значение).
Действие усреднения и благотворное (подавляет помехи), и вредное (может нежелательно подвергнуться усреднению искомая зависимость). Поэтому методы обработки экспериментальных зависимостей с помехами
всегда предполагают наличие компромисса: подавить помехи, но не
слишком сильно, чтобы не сгладить искомую зависимость. Ниже рассмотрим два метода.
2. Метод скользящего среднего
Назначение метода скользящего среднего для обработки кривых разгона, снимаемых на объекте для последующего получения математической модели, – облегчить подбор уравнений, описывающих процесс в
объекте, и расчет оценки коэффициентов этих уравнений (параметров
модели). Для того чтобы произвести такие действия, целесообразно обработать экспериментальную кривую разгона (рис. 1.5) так, чтобы получить более гладкую кривую (рис. 1.4). Подбор уравнений и расчет параметров для гладких кривых сделать гораздо легче, чем при использовании результатов эксперимента, загрязненных помехами. Причина состоит
в том, что для получения математической модели объекта часто необходима операция дифференцирования, которая при наличии высокочастотных помех выполняется с большими погрешностями: по существу действие даже небольшой высокочастотной помехи делает кривую многоэкстремальной, и в каждой точке экстремума производная будет изменять знак; а поскольку помеха высокочастотная – абсолютные значения
производной будут изменяться в широких пределах, что совершенно не
соответствует свойствам производных искомой гладкой функции.
2.1. Необходимые теоретические сведения
2.1.1. Содержательная постановка задачи. Представим себе, что в
результате эксперимента получены точки кривой разгона, загрязненные
измерительными помехами (рис. 2.1а). Кривая разгона является реакцией
объекта (изменение температуры), вызванной ступенчатым изменением
управляющего воздействия (сопротивления в обмотке возбуждения электропривода питателя печи, см. практическое занятие № 1, рис. 1.3). График
изменения управляющего воздействия показан в верхней части рисунка.
Измерительные помехи маскируют «природную», свойственную
объекту зависимость, которую глаз исследователя легко прорисует на
фоне помех (рис. 2.1б).
Поставим задачу создания алгоритма, который также может выявить
эту зависимость.
26
Сопротивление, Ом
Экспериментальные
точки
Экспериментальные
точки
Температура, оС
Сопротивление, Ом
Температура, оС
Экспериментальныеточки
точки
Экспериментальные
а) экспериментальная кривая разгона
Искомая
Искомаязависимость
зависимость
б) зависимость, которую нужно выявить
Рис. 2.1. К постановке задачи сглаживания экспериментальных зависимостей
2.1.2. Основная идея алгоритма. Алгоритм скользящего среднего является прозрачным обобщением известного из курса физики правила
трех измерений (нужно сделать три измерения и в качестве результата
взять среднее значение результатов измерений).
Фазы алгоритма метода показаны на рис. 2.2. Пусть выбрано нечетное количество экспериментальных точек (чтобы явно можно было выделить центральную точку). В примере, рассматриваемом на рис. 2.2, выбрано число точек, равное 5.
 Фаза 1, рис. 2.2а: выбираем первые (по времени) 5 точек, охватываем их «окном усреднения».
 Фаза 2, рис. 2.2б: находим среднее значение точек, попавших в
«окно». Показываем это значение (его абсцисса равна абсциссе
срединной точки «окна», в рассматриваемом примере – третьей).
Точка, соответствующая усредненному значению, показана крестиком.
 Фаза 3, рис. 2.2в: сдвигаем «окно усреднения» на одну точку. При
этом первая точка зависимости из окна уйдет, а вместо нее в окно
попадет следующая точка зависимости. Снова рассчитаем среднее
значение и покажем его на графике.
 Дальнейшие фазы аналогичны: сдвигаем «окно усреднения»,
рассчитываем среднее значение по точкам в «окне», показываем
это значение на графике.
27
Мы видим, что в результате таких действий прорисовывается гораздо более гладкая зависимость (рис. 2.2е).
Рис. 2.2. Фазы алгоритма скользящего среднего
2.1.3. Формальные соотношения являются обобщением идеи п. 2.1.2
на произвольное нечетное число точек в «окне усреднения». Приведем
их применительно к экспериментальной кривой разгона, показанной на
рис. 1.5.
~
Обозначим hi (i = 1, …, n) – значение кривой разгона в момент времени ti.
Выберем четное число L интервалов времени (тогда число точек в
этом интервале окажется нечетным).
Рассчитаем среднее значение hi по точкам, попавшим в «окно усреднения», и будем строить усредненную зависимость, заменяя эксперимен~
тальное значение hi усредненным значением hi:
28
L
2
~
1
hi 
  hi  j .
L  1 j  L
(2.1)
2
Например, если L = 4 (усреднение по 5-ти точкам), то
1 ~ ~ ~ ~ ~
h5   (h3  h4  h5  h6  h7 ) .
5
Замечание: формула (2.1) неприменима на первых (i = 1, 2, …, L/2) и последних
(i = n – L/2, …, n) точках. Поэтому экспериментальные точки нужно получить «с запасом». В частности, для кривых разгона следует получать «запасные» точки в режимах «старой» и «новой» статики.
2.1.4. Рекомендации по числу (L+1) точек в «окне усреднения». Нужно помнить, что в общем случае L выбирается под действием двух противоположных тенденций:
– если L слишком мало, то подавление помех будет недостаточным;
– если L слишком велико, то подавление помех будет отличным, но
заодно подвергнется усреднению и искомая зависимость.
Поэтому компромисс находим подбором, пока глазу исследователя
не покажется, что усреднение хорошее. Не следует бояться, что рекомендация ненаучная: исследователь всегда представляет себе физические основы работы объекта и поэтому примерно знает, какую форму имеет искомая зависимость.
Ориентировочные цифры:
– если число экспериментальных точек невелико (n < 30), то начинать расчеты нужно со значения L = 2 и постепенно увеличивать L (пока
не выявится «замаскированная» зависимость);
– если число экспериментальных точек велико (n >100), то начинать
расчеты можно с ближайшего снизу четного значения к величине n/2.
На рис. 2.3 показаны различные варианты выбора числа точек в
«окне усреднения» – от явно недостаточного до явно избыточного.
29
L=2
L=4
L = 10
L = 16
L = 26
L = 46
Рис. 2.3. Влияние числа точек в «окне усреднения» на эффективность метода скользящего
среднего
3. Метод четвертых разностей
Назначение метода – то же, что и метода скользящего среднего: облегчить подбор уравнений, описывающих процесс в объекте, и расчет
оценки коэффициентов этих уравнений (параметров модели) за счет
сглаживания помех, искажающих результаты эксперимента.
3.1. Необходимые теоретические сведения
3.1.1. Основная идея метода иллюстрируется рис. 2.4. Пусть имеются экспериментальные точки.
 Фаза 1, рис. 2.4а: выберем 5 текущих точек, окружим их «окном
усреднения».
30
 Фаза 2, рис. 2.4б: используя координаты 5-ти точек, рассчитаем
коэффициенты такой параболы, чтобы среднее квадратическое отклонение координат параболы от точек в окне было минимальным
(применяется метод наименьших квадратов).
 Фаза 3, рис. 2.4в: построим рассчитанную параболу и примем ее
центральную точку в качестве координаты, сглаживающей значение центральной точки «окна усреднения».
 Фаза 4 и последующие фазы, рис. 2.4г: сдвигаем окно на одну
точку и повторяем те же действия: рассчитываем коэффициенты
параболы, строим ее и принимаем ее центральную точку в качестве
координаты, сглаживающей значение центральной точки окна
усреднения.
Значения выхода объекта
Значения выхода объекта
В результате получится эффект сглаживания экспериментальных точек (сглаженные точки на рис. 2.4 обведены).
Номера экспериментальных точек
Номера экспериментальных точек
Рис. 2.4. Фазы алгоритма четвертых разностей
31
Значения выхода объекта
Значения выхода объекта
Номера экспериментальных точек
Номера экспериментальных точек
Окончание рис. 2.4. Фазы алгоритма четвертых разностей
3.1.2. Формальные соотношения. (Получение соотношений для метода четвертых разностей предоставляется студентам для самостоятельного изучения).
~
Обозначим hi (i = 1, …, n) – значение кривой разгона в момент времени ti.
Для i = 2, 3, …, n – 2 координаты точек усредненной зависимости
рассчитываются по формуле:
~
~
~
~
~
1
(2.2)
hi   (hi  2  4  hi 1  6  hi  4  hi 1  hi  2 ) .
12
Для начальных и концевых точек (i = 0, 1, n-1, n) формулы имеют вид:
~
~
~
~
~
1
(2.3)
h0   (53  h0  16  h1  6  h2  8  h3  5  h4 ),
60
~
~
~
~
~
1
(2.4)
h1   (9  h0  13  h1  12  h2  6  h3  5  h4 ),
35
~
~
~
~
~
1
(2.5)
hn1   (9  hn  13  hn1  12  hn2  6  hn3  5  hn4 ),
35
~
~
~
~
~
1
(2.6)
hn 
 (53  hn  16  hn 1  6  hn  2  8  hn 3  5  hn  4 ) .
60
3.1.3. Настраиваемый параметр метода четвертых разностей – число
проходов алгоритма: если после первого прохода построенная зависимость
окажется недостаточно гладкой, нужно повторить процедуру, используя результат предыдущего сглаживания в качестве исходных данных.
32
4. Сравнение методов скользящего среднего и четвертых разностей
Расчеты показывают, что при большом числе точек и высокочастотных измерительных помехах метод скользящего среднего предпочтительнее метода четвертых разностей.
При малом числе экспериментальных точек и при наличии низкочастотных помех, наоборот, метод четвертых разностей предпочтительнее
метода скользящего среднего.
5. Оценка параметров модели объекта по сглаженной кривой разгона
5.1. Основная идея оценки параметров модели методом площадей
состоит в таком подборе параметров, чтобы площадь под «перевернутой»
экспериментальной кривой разгона была такой же, как площадь под «перевернутой» расчетной кривой, полученной на модели. Поясним идею
примером оценки постоянной времени модели в форме апериодического
звена первого порядка:
dx(t )
(2.7)
T0 
 x(t )  k 0  u (t ) ,
dt
где T0 – постоянная времени модели;
k0 – коэффициент усиления модели (подробнее см. описание практического занятия № 1).
Решение дифференциального уравнения (2.7) для случая, когда на
вход объекта подается ступенчатое воздействие, имеет вид:
t
 

(2.8)
x(t )  k0  1  e T0   u2  u1  ,




где Δx(t) = x(t) – x(0);
x(0) – значение выхода объекта в режиме «старой» статики, соответствующей входу u1, скачком изменившемуся до значения u2 при t = 0.
Поясним основную идею на примере определения параметров этой
простейшей модели (рис. 2.5).
1. Пусть в результате опытов на реальном объекте получена экспериментальная кривая разгона. Сгладим ее (одним из методов, рассмотренных ранее) и в предположении о том, что коэффициент усиления объекта известен (способ определения описан ниже), приведем ее к диапазону 0...1 (рис. 2.5а).
2. Площадь под кривой (рис. 2.5а) определить нельзя, т. к. кривая не
образует ограниченную область. Поэтому «перевернем» ее, вычитая ее
значения из единицы. Получим кривую рис. 2.5б.
3. Рассчитаем площадь SЭ под ней (например, методом прямоугольников, см. ниже).
33
Перевернутая экспериментальная кривая разгона
Сглаженная экспериментальная кривая разгона
Расчетная кривая разгона
по модели 1-го порядка
Перевернутая расчетная
кривая разгона по модели
1-го порядка
Необходимо подобрать постоянную времени То
так, чтобы эти площади были равны
Рис. 2.5. Пояснение к методу площадей
4. Определим расчетную кривую разгона, приведенную к единичному диапазону, по модели (2.8) в форме:

t
T0
.
(2.9)
xединичн (t )  1  e
5. Мы видим, что значения кривой (2.9) зависят от постоянной времени T0.
6. Если расчетную кривую (рис. 2.5в) перевернуть (рис. 2.5г), то
можно подобрать T0 так, чтобы площади под кривыми (рис. 2.5б и
рис. 2.5г) были одинаковыми. Тогда можно надеяться, что расчетная и
экспериментальная кривые будут сходными.
7. Площадь SM под кривой (2.9) находится аналитически:


S M   1  xединичн (t )dt   e
0

t
T0
dt  T0 .
(2.10)
0
8. Таким образом, постоянную времени модели (2.7) можно оценить
по площади SЭ под нормированной (т. е. приведенной к единичному диапазону) «перевернутой» сглаженной экспериментальной кривой разгона.
9. Для расчета SЭ можно использовать метод прямоугольников
(рис. 2.6): интервал времени tпр, на котором «перевернутая» эксперимен34
тальная кривая заметно отличается от 0, разбивается на q равных отрезков
продолжительностью t, и затем строятся прямоугольники с основаниями
t и высотами, соответствующими значениям экспериментальной кривой
на левой границе прямоугольников. Площади прямоугольников суммируются.
Рис. 2.6. Вычисление площади под «перевернутой» экспериментальной кривой разгона
10. После расчета получаем значение параметра модели:
(2.11)
T0  S Э .
11. Осталось пояснить, как найти коэффициент усиления объекта.
Для этого используем формулу:
x
x
(2.12)
k0  нов _ стат стар _ стат ,
u2  u1
где xнов_стат, xстар_стат – соответственно значения выхода объекта в режимах «новой» и «старой» статики;
u2, u1 – значения входного воздействия, изменяющегося скачком от значения u1, соответствующего «старой» статике, до значения u2, соответствующего «новой» статике.
Замечания:
1. Основным преимуществом метода площадей является его малая чувствительность к неточностям экспериментальной кривой разгона: при интегрировании
эти неточности сглаживаются.
2. Для использования более сложных моделей (второго порядка и выше) метод
остается применимым, но необходимо повторное интегрирование «перевернутой» кривой разгона.
3. Оценку запаздывания лучше всего проводить «на глаз»: сдвинуть экспериментальную кривую разгона так, чтобы устранить влияние запаздывания на ее график, а затем включить запаздывание в окончательную форму модели.
Если проделать расчеты параметров модели 1-го порядка по кривой
разгона, полученной на виртуальном объекте, который был рассмотрен
35
на практическом занятии № 1, то мы увидим, что модель имеет невысокую
точность (рис. 2.7). Мы видим признаки недостаточности порядка модели
(2.7): начальная часть расчетной кривой имеет более высокую скорость
нарастания, а концевая – более низкую, чем у экспериментальной кривой
(хотя и видно, что площади под перевернутыми кривыми примерно равны). Целесообразно попытаться использовать модель более высокого порядка и учесть запаздывание.
Рис. 2.7. Сравнение экспериментальной кривой разгона с расчетной, полученной при
использовании модели 1-го порядка
6. Контрольные вопросы
Зачем сглаживать кривые разгона, полученные экспериментально?
Какие методы сглаживания экспериментальных зависимостей
Вы знаете?
3. Какова основная идея алгоритма скользящего среднего?
4. Почему число интервалов времени в алгоритме скользящего
среднего должно быть четным?
5. Каковы рекомендации по выбору числа точек в «окне усреднения» при использовании алгоритма скользящего среднего?
6. Какова основная идея метода четвертых разностей?
7. Что является настраиваемым параметром метода четвертых разностей?
8. В каком случае метод скользящего среднего предпочтительнее
метода четвертых разностей? В каком случае метод четвертых
разностей предпочтительнее метода скользящего среднего?
9. Какие этапы нужно выполнить для идентификации динамической характеристики методом площадей?
10. Что такое нормированная кривая разгона?
1.
2.
36
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 3
ТЕМА: «ПОСТРОЕНИЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ. ПОНЯТИЕ
ОБ УПРАВЛЕНИИ С ОБРАТНОЙ СВЯЗЬЮ»
Время проведения практического занятия (аудиторные часы) – 2 часа.
Время самостоятельной работы студента (дополнительные часы) – 2 часа.
Цели занятия: ознакомиться с методом построения передаточной
функции САУ по ее дифференциальному уравнению и с выполнением
обратной операции (построение дифференциального уравнения по передаточной функции); получить представление о назначении и существе
САУ с отрицательной обратной связью.
Рассматриваемые вопросы:
1. Закрепление понятия «передаточная функция САУ».
2. Пример построения передаточной функции по дифференциальному уравнению САУ.
3. Пример построения дифференциального уравнения по передаточной функции САУ.
4. Качественные особенности замкнутой САУ с обратной связью.
Существо управления с обратной связью.
1. Определение передаточной функции САУ
Понятие «передаточная функция» введено в связи с использованием
аппарата преобразования Лапласа, благодаря которому в пространстве
изображений по Лапласу удается понизить сложность описания процессов в САУ (перейти от дифференциальных уравнений к алгебраическим).
Покажем два способа представления САУ: в исходном пространстве
(аргумент – время, язык описания – дифференциальные уравнения) и в
пространстве изображений (аргумент – оператор Лапласа, язык описания – алгебраические уравнения (рис. 3.1)).
1. В исходном пространстве (аргумент – время)
Вход u(t)
Объект и
система
управления
Выход y(t)
2. В пространстве изображений (аргумент – оператор Лапласа)
Изображение
входа U(p)
Передаточная функция объекта и системы
управления W(p)
Изображение
выхода Y(p)
Рис. 3.1. Иллюстрация понятия «передаточная функция САУ»
37
Определение: передаточной функцией САУ W(p) называется отношение изображения (по Лапласу) выхода системы Y(p) к изображению
входа U(p).
Y ( p) .
(3.1)
W ( p) 
U ( p)
Область применения понятия – тройка ограничений:
1. САУ обязательно являются линейными.
2. Параметры САУ не зависят от времени.
3. Начальные условия являются нулевыми.
2. Пример построения передаточной функции САУ
по ее дифференциальному уравнению
Пусть модель САУ задана в терминах «вход–выход», все переменные – скаляры; пусть модель имеет форму дифференциального уравнения
3-го порядка:
a0 
d 3 y (t )
d 2 y(t )
dy (t )
d 2u (t )
du (t )
 a1 
 a2 
 a3  y(t )  b1 
 b2 
 b3  u (t ) . (3.2)
3
2
dt
dt
dt
dt 2
dt
Пусть начальные условия – нулевые:
dy(t )
d 2 y(t )
y(t ) t 0  0,
 0,
 0.
dt t 0
dt 2 t 0
Тогда изображение по Лапласу для производных в (3.2) примет вид
умножения на оператор Лапласа в степени, соответствующей порядку
производной:
 d 2 y (t ) 
 d 3 y (t ) 
 dy (t ) 
  p 2  Y ( p ); L
  p 3  Y ( p);
L
  p  Y ( p); L
2
3
dt
dt
 dt 




 d 2 u (t ) 
 du (t ) 
  p 2  U ( p ).
L
  p  U ( p ); L
2
 dt 
 dt 
Подставляя изображения в (3.2), получим:
a0  p 3  Y ( p)  a1  p 2  Y ( p)  a2  p  Y ( p)  a3  Y ( p) 
 b1  p 2  U ( p)  b2  p  U ( p)  b3  U ( p).
Помня, что после преобразования Лапласа получено алгебраическое
уравнение, вынесем за скобки Y(p) и U(p):
(a0  p 3  a1  p 2  a 2  p  a3 )  Y ( p)  (b1  p 2  b2  p  b3 )  U ( p). (3.3)
С помощью (3.3) найдем передаточную функцию:
b1  p 2  b2  p  b3
Y ( p)
.
(3.4)
W ( p) 

U ( p) a0  p 3  a1  p 2  a2  p  a3
Мы видим, что в простейших случаях передаточная функция представляет собой дробь, числитель и знаменатель которой – полиномы
38
оператора Лапласа, степень числителя в подавляющем числе случаев не выше (обычно – ниже) степени знаменателя.
Примечание: в более сложных случаях передаточная функция содержит иррациональные и трансцендентные функции (в частности, если объект управления содержит запаздывание и / или распределенные параметры, т. е. описывается дифференциальными уравнениями с частными производными).
3. Пример построения дифференциального уравнения САУ
по ее передаточной функции
Технология построения:
1. Используя передаточную функцию, записать: [Знаменатель передаточной функции]Y(p) = [Числитель передаточной функции]U(p).
2. Раскрыть скобки.
3. Перейти от изображений производных к оригиналам: вместо
k
m
pk·Y(p), pm·U(p) записывать d y (t ) , d u (t ) , получим дифференциальное
dt k
dt m
уравнение САУ в терминах «вход–выход».
Пример: пусть структура САУ содержит объект (модель 2-го порядка без запаздывания) и регулятор в цепи обратной связи (рис. 3.2). Заданы передаточные функции объекта и регулятора. Мы видим, что в состав
структуры САУ входят:
1) апериодическое звено 2-го порядка (передаточная функция объекта);
2) безынерционное звено и соединённое с ним параллельно интегрирующее звено (передаточная функция регулятора).
Считаем, что параметры объекта ko, T1, T2 (соответственно – коэффициент усиления и постоянные времени) и параметры регулятора kp, ki
(как мы узнаем на практическом занятии № 5 – коэффициенты при пропорциональной и интегральной части закона управления) известны.
Поставим задачу: сформировать дифференциальное уравнение САУ
по заданным передаточным функциям ее элементов и по схеме их соединения. В данном случае вид соединения – звено, охваченное отрицательной обратной связью.
Шаг 1. Используя теорему алгебры структурных преобразований
для звена, охваченного отрицательной обратной связью, записываем передаточную функцию САУ по каналу «задающее воздействие g(t) (задано
изображением по Лапласу G(p)) – выход y(t) (задан изображением по
Лапласу Y(p))». Прямая цепь представлена последовательным соединением регулятора и объекта, цепь обратной связи – безынерционным звеном
с коэффициентом усиления единица. Для того чтобы это было легче понять, полезно перерисовать схему рис. 3.2 так, как на рис. 3.3.
39
Изображение
управляющего
воздействия
U(p)
Изображение
выхода объекта Y(p)
Объект:
Wo ( p) 
ko
T1  T2  p 2  (T1  T2 )  p  1
G(p) – изображение
задающего
воздействия
Регулятор:
W рег ( p)  k p 
ki
p
Рис. 3.2. Структурная схема САУ, изображенная с помощью передаточных функций
ее элементов
Прямая цепь
G(p)
U(p)
Регулятор:
Объект:
k
W рег ( p)  k p  i
p
Wo ( p) 
ko
T1  T2  p 2  (T1  T2 )  p  1
Y(p)
1
Цепь отрицательной обратной связи
Рис. 3.3. Структурная схема САУ с показом прямой цепи и цепи отрицательной обратной
связи
W ( p) 
Wпрям_ цепи ( p)
1  Wпрям_ цепи ( p)  Wцепи _ обр _ св ( p)

W рег ( p)  Wо ( p)
1  W рег ( p)  Wо ( p)
После упрощений получаем:
k o  (k p  p  ki )
.
W ( p) 
3
T1  T2  p  (T1  T2 )  p 2  (1  ko  k p )  p  k o  ki
.
(3.5)
Шаг 2. Записываем связь изображения входа с изображением выхода согласно (3.1):
Y ( p)  W ( p)  G( p) 

k o  (k p  p  k i )
T1  T2  p  (T1  T2 )  p 2  (1  k o  k p )  p  k o  k i
3
40
 G ( p),
T  T
1
2

 p 3  (T1  T2 )  p 2  (1  k o  k p )  p  k o  ki  Y ( p) 
 k o  (k p  p  ki )  G ( p ),
T1  T2  p 3  Y ( p)  (T1  T2 )  p 2  Y ( p)  (1  k o  k p )  p  Y ( p)  k o  k i  Y ( p) 
 k o  k p  p  G ( p)  k i  G ( p).
(3.6)
Шаг 3. Используем обратное преобразование Лапласа для получения дифференциального уравнения САУ. Вместо pk·Y(p), pm·G(p) запиk
m
шем d y (t ) , d g (t ) :
k
dt
dt m
d 3 y (t )
d 2 y (t )
dy (t )
T1  T2 
 (T1  T2 ) 
 (1  k o  k p ) 
 k o  k i  y (t ) 
3
dt
dt
dt 2
dg (t )
(3.7)
 ko  k p 
 k i  g (t ).
dt
4. Качественные особенности замкнутой САУ с обратной связью.
Существо управления с обратной связью
Роль, которую система управления играет в общем процессе функционирования объекта, относится к одному из двух классов:
1. Подавление возмущений (как внешних, так и параметрических).
2. Ускорение динамических процессов.
Рассмотрим сначала класс 1 (подавление возмущений).
Пусть имеется объект, технологической целью которого является
обеспечение заданного (и длительно постоянного во времени) значения
выхода (например, температуры нагрева). Если бы возмущающие воздействия отсутствовали, то обратная связь была бы не нужна: можно было
бы подобрать такое значение входного сигнала, при котором выход соответствовал бы заданию (рис. 3.4).
Рис. 3.4. Если возмущений нет, то достигается соответствие выхода заданию
без САУ с обратной связью
41
Управление объектом без специальной системы экономически целесообразно, и если разработчик уверен, что, во-первых, на объект не будут
действовать заметные возмущения и, во-вторых, технологический режим работы объекта будет таким, что интервал продолжительности постоянства задающего воздействия значительно длиннее интервала переходного процесса в объекте, то именно такой вариант управления и следует применить. В качестве примера можно указать кухонную духовку. Внешние
возмущения (температура на кухне) пренебрежимо малы по сравнению с
температурой внутри нагретой духовки, поэтому часто средства измерения
температуры в духовку не встраивают, ограничиваются градуированным
задатчиком интенсивности пламени (самый дешевый вариант).
Но посмотрите, как изменится результат работы объекта, если в момент времени tВ на вход объекта поступит внешнее постоянное (рис. 3.5а)
или переменное во времени (рис. 3.5б) возмущающее воздействие. Поскольку возмущения и задающие воздействия поступают на вход объекта
суммарно (и равноправно), то выход объекта отклонится от задания, и его
функционирование не будет соответствовать технологической цели.
Запомним: при наличии сильных внешних неизмеряемых возмущений САУ с обратной связью необходима для того, чтобы могла быть
достигнута технологическая цель функционирования объекта.
а) реакция объекта (САУ отсутствует) на
ступенчатое возмущающее воздействие
б) реакция объекта (САУ отсутствует) на
возмущающее воздействие, переменное во
времени
Рис. 3.5. При наличии сильных внешних неизмеряемых возмущений управление без САУ с
обратной связью неэффективно
Еще большую опасность для работы объекта представляют внутренние возмущения (обычно имеют форму медленного изменения во времени по разным причинам – например, вследствие износа оборудования,
изменения свойств катализатора и т. п.). На рис. 3.6а показан результат
действия медленного во времени линейного «сползания» коэффициента
усиления объекта ko. Мы видим, что выход объекта не соответствует за42
данию. Если же линейное «сползание» коэффициента усиления сопровождается медленными периодическими изменениями (рис. 3.6б), то появляется катастрофическое явление – неустойчивость.
а) реакция объекта (САУ отсутствует) на
линейный во времени дрейф коэффициента
усиления объекта
б) реакция объекта (САУ отсутствует) на
дрейф коэффициента усиления в виде суммы
линейной и периодической составляющих
Рис. 3.6. При наличии даже небольших внутренних (параметрических) возмущений
управление объектом без САУ с обратной связью не только неэффективно, но может
привести к неустойчивости
Запомним: при наличии даже слабых внутренних (параметрических) возмущений САУ с обратной связью необходима для того, чтобы
могла быть достигнута технологическая цель функционирования объекта.
Для доказательства необходимости САУ с отрицательной обратной
связью приведем графики работы такой САУ с регулятором, передаточная функция которого показана на рис. 3.2. На графиках (рис. 3.7) иллюстрируется работа САУ с регулятором в сравнении с работой объекта без
системы управления при наличии внешних возмущений. Мы видим, что
САУ подавляет внешние возмущения, обеспечивая достижение технологической цели работы объекта. Показан (как и на рис. 3.5) случай, когда в
момент времени tВ на вход объекта поступает внешнее постоянное (рис.
3.7а) или переменное во времени (рис. 3.7б) возмущающее воздействие.
САУ с обратной связью способна также подавлять и внутренние (параметрические) возмущения, если они не слишком велики (в противном
случае возникает опасность неустойчивости; но и для этого случая теория управления имеет средства: САУ нужно проектировать как адаптивную, у такой САУ будет свойство перестраивать структуру и / или
настроечные параметры регулятора при изменениях параметров объекта).
На рис. 3.8 иллюстрируется подавление линейного (рис. 3.8а) и линейного с периодической составляющей (рис. 3.8б) тренда коэффициента усиления объекта. Мы видим, что качество выполнения технологической цели управления при наличии САУ достигается.
43
а) подавление внешнего ступенчатого
возмущающего воздействия
б) подавление внешнего периодического
возмущающего воздействия
Рис. 3.7. САУ с обратной связью подавляет внешние возмущения (для сравнения показан
выход объекта при отсутствии САУ)
а) подавление внутреннего возмущения
(линейного дрейфа коэффициента усиления
объекта)
б) подавление внутреннего возмущения
(дрейфа коэффициента усиления объекта с
линейной и периодической составляющими)
Рис. 3.8. САУ с обратной связью подавляет внутренние (параметрические) возмущения
(для сравнения показан выход объекта при отсутствии САУ)
Перейдем к рассмотрению класса 2 задач, в которых необходимо
наличие системы управления (ускорение динамических процессов). На
первый взгляд такая постановка задачи вызывает вопрос: каким же образом получается, что регулятору («энергетическому ничтожеству» по
сравнению с мощностью объекта) удается осуществлять функцию управления? Нужно обратить внимание на то, что при прорисовке схемы системы управления энергетические аспекты совсем не отражаются (конечно, и регулятор, и иные устройства управления потребляют некоторое
количество энергии, но оно пренебрежимо мало по сравнению с энергетическими потоками, которыми оперирует объект).
44
Ответ состоит в том, что САУ работает за счет «обмана» объекта.
Пояснения – на рис. 3.9. Если в отсутствие САУ с обратной связью подать на вход объекта нужное значение задающего воздействия, то при отсутствии возмущений выход практически придет к заданию за время tnatur
(рис. 3.9а). САУ «обманывает» объект, подавая на его вход расчетное, искусственное задающее воздействие, превышающее нужное. Поэтому (рис.
3.9б) нужное значение будет достигнуто за гораздо меньшее время
tforc << tnatur (рис. 3.9б). Конечно, нужно всё время изменять это «искусственное» задание так, чтобы привести выход объекта к окрестности заданного значения; этим и занимается система автоматического управления.
Рис. 3.9. Система автоматического управления подает на вход «искусственное» задающее
воздействие, заставляя объект быстрее достичь нужного значения задающего воздействия
Поясним термин «окрестность заданного значения». На практике
нельзя требовать точного соответствия выхода объекта заданию (из-за
неизбежных помех и неточностей это невозможно). Оговаривается (в
техническом задании на создание САУ) максимально возможное отклонение от задания. Тогда задающее воздействие превращается в «трубку
статики» (рис. 3.10): переходный процесс от «старой» к «новой» статике
считается завершенным после момента времени t*, начиная с которого
колебания выхода объекта всегда остаются внутри «трубки статики». Показатель t* называется временем переходного процесса. Нужно пояснить,
что он субъективно зависит от того, какой размер трубки статики считается приемлемым.
Сравним время переходного процесса в САУ с обратной связью с
условиями работы объекта без САУ. Мы видим (рис. 3.10а), что время переходного процесса tcontrol при наличии САУ существенно (почти в 2 раза)
меньше времени переходного процесса tfree для объекта без САУ. Еще убедительнее выявляются преимущества САУ для ускорения процессов в объекте при отработке переменного во времени задающего воздействия (рис.
3.10б): объект без САУ безнадежно отстает от изменения задания, а при
наличии САУ качество воспроизведения задания остается хорошим.
45
Рис. 3.10. Система автоматического управления ускоряет реакцию объекта на изменения
задающего воздействия
Запомним: при работе объекта в условиях частых изменений задающих воздействий САУ с обратной связью необходима для ускорения реакции объекта на эти изменения и для того, чтобы объект мог
выполнить технологическую цель своего функционирования.
5. Контрольные вопросы
Что такое передаточная функция?
Для чего используются передаточные функции?
Каковы ограничения, накладываемые на область применения понятия передаточная функция?
4. Какова технология построения дифференциального уравнения
САУ по ее передаточной функции?
5. Что такое алгебра структурных преобразований, зачем ее вводят?
6. Как рассчитать передаточную функцию последовательно соединенных звеньев (если передаточная функция каждого известна)?
7. Как рассчитать передаточную функцию параллельно соединенных звеньев (если передаточная функция каждого известна)?
8. Как рассчитать передаточную функцию САУ, охваченной обратной связью?
9. Чем отличается передаточная функция САУ, охваченной отрицательной обратной связью, от передаточной функции САУ, охваченной положительной обратной связью?
10. Какова роль, которую система управления играет в общем процессе функционирования объекта?
1.
2.
3.
46
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 4
ТЕМА: «СТРУКТУРНЫЕ ПРЕОБРАЗОВАНИЯ САУ
С ПЕРЕКРЕСТНЫМИ СВЯЗЯМИ»
Время проведения практического занятия (аудиторные часы) – 2 часа.
Время самостоятельной работы студента (дополнительные часы) – 2 часа.
Цель занятия: изучить метод определения общей передаточной
функции САУ с перекрестными связями (на примере).
Рассматриваемые вопросы:
1. Технология структурных преобразований САУ с перекрестными
связями.
2. Понятие о принципе суперпозиции и его применении для нахождения передаточных функций системы со многими входными воздействиями.
3. Подробное рассмотрение примера построения общей передаточной функции САУ по каналам:
a) «задающее воздействие – выход объекта»;
b) «задающее воздействие – рассогласование между заданием и
выходом объекта»;
c) «возмущающее воздействие – выход объекта»;
d) «возмущающее воздействие – рассогласование между заданием и выходом объекта».
1. Технология структурных преобразований САУ
с перекрестными связями
Определение 1. Многоконтурной системой без перекрестных связей
(другое название – простая многоконтурная САУ) называется такая, в
которой внешние параллельные звенья и / или внешние звенья обратных
связей охватывают И начало, И конец другого участка внутренних цепей
с параллельными звеньями и / или внутренних цепей обратных связей.
Технология расчета общей передаточной функции состоит в использовании теорем алгебры структурных преобразований (последовательное
соединение звеньев, параллельное соединение звеньев, передаточная
функция звена с обратной связью) от внутренних контуров – к внешним.
Определение 2. Многоконтурной системой с перекрестными связями
(другое название – многосвязная САУ) называется такая, в которой внешние параллельные звенья и / или внешние звенья обратных связей охватывают ТОЛЬКО начало, но НЕ конец или ТОЛЬКО конец, но НЕ
начало другого участка внутренних цепей с параллельными звеньями и /
или внутренних цепей обратных связей.
Технология расчета общей передаточной функции:
1. Перестановкой узлов и сумматоров добиться исключения перекрестных связей и получить простую многоконтурную САУ.
47
2. Определить общую передаточную функцию полученной простой
многоконтурной САУ.
2. Пример получения общей передаточной функции многоконтурной
САУ с перекрестными связями
2.1. Постановка задачи
Дано: структурная схема (рис. 4.1) и передаточные функции входящих в нее элементарных звеньев. На схеме показаны изображения задающего воздействия G(p), выхода системы Y(p) и возмущающего воздействия F(p). Оператор p в обозначениях передаточных функций звеньев
опущен.
Обозначения:
– звено сравнения;
Изображение
задающего
воздействия
G(p)
– сумматор;
– узел (развилка)
Изображение
рассогласования
(p) = G(p) – Y(p)
4
1
2
W1
W2
Изображение
выхода Y(p)
3
F(p)
W3
3
1
W5
W4
2
Рис. 4.1. Структурная схема многоконтурной САУ с перекрестными связями
Получить: общие передаточные функции САУ по каналам:
Канал 1: «задающее воздействие g(t) – выход объекта y(t)».
Канал 2: «задающее воздействие g(t) – рассогласование между задающим воздействием и выходом объекта (t) = g(t) – y(t)».
Канал 3: «возмущающее воздействие f(t) – выход объекта y(t)».
Канал 4: «возмущающее воздействие f(t) – рассогласование между
задающим воздействием и выходом объекта (t) = g(t) – y(t)».
2.2. Преобразование многоконтурной САУ с перекрестными связями в структуру простой многоконтурной САУ
Шаг 1. Замена последовательно соединенных звеньев W1 и W2 единым
звеном W12. Согласно теореме 1 алгебры структурных преобразований,
48
(4.1)
W12  W1 W2 .
Шаг 2. Перенос узла 3 против хода сигнала через объединенное
звено W12. Согласно теореме 4б алгебры структурных преобразований,
при этом должно быть вставлено такое же звено в цепь перенесенного
сумматора. Получим промежуточную структурную схему (рис. 4.2).
4
G(p)
(p) 3
2
4 Y(p)
W12
1
W5
W3
W12
3
W4
1
F(p)
2
Рис. 4.2. Результат переноса узла 3 против хода сигнала
Шаг 3. Перенос сумматора 3 по ходу сигнала за сумматор 4 через звенья W3 и W4. Согласно теореме 4а алгебры структурных преобразований,
вставляется звено W3∙W4. Получим промежуточную структурную схему
(рис. 4.3). Звенья W12 и W3 оказываются соединенными последовательно,
заменяем их одним звеном (согласно теореме 1 – произведением их передаточных функций).
F(p)
G(p)
W3W4
4
(p) 3
1
2
4
Y(p)
W1W2
W5
W1W2W3
3
W4
1
2
Рис. 4.3. Результат переноса сумматора 3 по ходу сигнала
Последующие шаги (рис. 4.4).
1. Переносим сумматор 1 по ходу сигнала через звено W4.
2. В цепь 1 – 4 добавляем звено W4.
3. Переносим сумматор 2 по ходу сигнала, переставляем с сумматором 1 и с сумматором 4 без вставки звеньев.
В результате получаем многоконтурную структуру без перекрестных связей (рис. 4.4).
49
Мы видим, что многоконтурная САУ с перекрестными связями в результате приобрела структуру простой многоконтурной САУ. Этап 1 завершен.
F(p)
W3W4
4
G(p)
(p) 3
1
2
3
1
2
4
W1W2
Y(p)
W5
W1W2W3W4
W4
Рис. 4.4. Окончание преобразования структуры с перекрестными связями в структуру
простой многоконтурной САУ
2.3. Получение общей передаточной функции по передаточным
функциям звеньев структуры простой многоконтурной системы
Производится (последовательно, начиная с самого внутреннего контура) вычисление общих передаточных функций параллельных соединений и структур с обратными связями.
Шаг 1. Замена контура с передаточными функциями W1, W2, W5
единым звеном.
(4.2)
W125  W1  W2  W5 .
Затем, пользуясь перестановочностью сумматоров, переносим сумматор 3 вместе со всеми входящими в него звеньями в позицию вне контуров параллельных звеньев. Получим структуру, показанную на рис. 4.5.
F(p)
1
G(p)
(p)
1
3
W3W4
2
3
W125
4
Y(p)
W1W2W3W4
W4
Рис. 4.5. Шаг 1 преобразования структуры простой многоконтурной САУ
50
Шаг 2. Замена контура с передаточными функциями W125 и W1234 =
= W1∙W2∙W3∙W4 единым звеном:
(4.3)
W12345  W125  W1234  W1 W2  W5  W1 W2  W3  W4 .
Шаг 3. Объединение контура, полученного в результате шага 2, и
параллельного контура с W4. Получим передаточную функцию прямой
цепи, объединяющую все параллельные контуры (рис. 4.6). Для пояснения в цепь обратной связи включено звено с единичной передаточной
функцией.
Wпрямой_ цепи  W12345  W4  W1  W2  W5  W1  W2  W3  W4  W4 
 W1  W2  W4  (1  W1  W2  W3 )  W5 .
F(p)
G(p)
(p)
(4.4)
W3W4
3
Wпрямой_цепи
4
Y(p)
1
Рис. 4.6. Структура САУ после выполнения шага 3
2.4. Принцип суперпозиции
Дальнейшие шаги зависят от того, для какого канала САУ нам нужно составить передаточные функции. Согласно заданию нужно рассмотреть 4 канала:
Канал 1: «задающее воздействие g(t) – выход объекта y(t)».
Канал 2: «задающее воздействие g(t) – рассогласование между задающим воздействием и выходом объекта (t) = g(t) – y(t)».
Канал 3: «возмущающее воздействие f(t) – выход объекта y(t)».
Канал 4: «возмущающее воздействие f(t) – рассогласование между
задающим воздействием и выходом объекта (t) = g(t) – y(t)».
В зависимости от того, какой из каналов изучается, нужно отбросить
«лишние» входы, используя принцип суперпозиции. Этот принцип
справедлив ТОЛЬКО для линейных систем (но и аппарат преобразования Лапласа, и, следовательно, аппарат передаточных функций также
применимы ТОЛЬКО для линейных систем).
Принцип суперпозиции: реакция системы на сумму внешних
воздействий равна сумме реакций системы на каждое воздействие в
отдельности. Принцип справедлив только для линейных систем.
51
В общей формулировке, применимой не только для систем автоматического управления: следствие суммы причин равно сумме следствий от каждой причины в отдельности.
2.5. Составление общей передаточной функции по каналу «задающее воздействие g(t) – выход объекта y(t)»
Согласно принципу суперпозиции исключим из рассмотрения «лишний» канал, связанный с возмущающим воздействием. Получим структуру, показанную на рис. 4.7.
G(p)
(p)
Wпрямой_цепи
Y(p)
1
Рис. 4.7. Структура САУ для канала «задающее воздействие – выход»
Используя теорему 3 алгебры структурных преобразований и формулу (4.4), получим передаточную функцию Wgy(p) по каналу «задающее
воздействие g(t) – выход объекта y(t)» (с учетом того, что звено обратной
связи имеет единичную передаточную функцию):
W1 ·W2  W4 ·(1  W1 ·W2 ·W3 )  W5 .
(4.5)
Wgy ( p) 
1  W1 ·W2  W4 ·(1  W1 ·W2 ·W3 )  W5
2.6. Составление общей передаточной функции по каналу «задающее воздействие g(t) – рассогласование (t)»
Полезно научиться приему, с помощью которого структура канала
становится ясной (см. рис. 4.8): растягиваем линию от звена сравнения к
рассогласованию (она теперь будет выходом изучаемого канала). Перерисовываем соединения между рассогласованием, прямой цепью и звеном сравнения, в результате чего увидим, что Wпрямой_цепи попадает в контур обратной связи этого канала. Для наглядности вставляем единичное
звено между звеном сравнения и рассогласованием, получаем структуру
рис. 4.8.
(p)
G(p)
1
Y(p)
Wпрямой_цепи
Рис. 4.8. Структура САУ для канала «задающее воздействие – рассогласование»
Используя теорему 3 алгебры структурных преобразований и формулу (4.4), получим передаточную функцию Wg(p) по каналу «задающее
52
воздействие g(t) – рассогласование между задающим воздействием и выходом объекта (t) = g(t) – y(t)» (с учетом того, что звено прямой цепи
рис. 4.8 имеет единичную передаточную функцию, а звено отрицательной обратной связи – передаточную функцию Wпрямой_цепи):
1
.
(4.6)
Wg ( p) 
1  W1 ·W2  W4 ·(1  W1 ·W2 ·W3 )  W5
2.7. Составление общей передаточной функции по каналу «возмущающее воздействие f(t) – выход y(t)»
Используя принцип суперпозиции, исключим из рассмотрения задающее воздействие (положим g(t) = 0). Получим рис. 4.9 (вместо схемы
рис. 4.6):
F(p)
(p)
W3W4
3
4
Wпрямой_цепи
Y(p)
Рис. 4.9. Исходная структура САУ для вычисления передаточной функции
по каналу «возмущение – выход»
Шаг 1. Используя теорему 8 алгебры структурных преобразований,
переставляем сумматор с узлом. Получим рис. 4.10:
3
(p)
Y(p)
4
Wпрямой_цепи
3
W3W4
F(p)
Рис. 4.10. Структура САУ для вычисления передаточной функции
по каналу «возмущение – выход» после шага 1
Шаг 2. Учитывая, что звено сравнения изменяет знак суммирования,
получим окончательно структуру, по которой найдем искомую передаточную функцию (рис. 4.11).
F(p)
F(p)
– W3W4
(p)
4
W3W4
3
Wпрямой_цепи
1
Рис. 4.11. Структура САУ для вычисления передаточной функции
по каналу «возмущение – выход» после шага 2
53
Y(p)
Шаг 3. Вычисляем передаточную функцию, суммируя действие
возмущения (попадающего на выход через 2 канала):
W ·W  W4 ·(1  W1·W2 ·W3 )  W5
W fy ( p)  (W3 ·W4 · 1 2
 W3 ·W4 ) 
1  W1·W2  W4 ·(1  W1·W2 ·W3 )  W5
 W3 ·W4 ·(1 
W1·W2  W4 ·(1  W1·W2 ·W3 )  W5
)
1  W1·W2  W4 ·(1  W1·W2 ·W3 )  W5
1
 W3 ·W4 ·
.
1  W1·W2  W4 ·(1  W1·W2 ·W3 )  W5
(4.7)
2.8. Составление общей передаточной функции по каналу «возмущающее воздействие g(t) – рассогласование (t)»
Снова «выворачиваем» схему так, чтобы выходом структуры оказалось рассогласование. Мы видим, что второй канал действия возмущений
не оказывает влияния на рассогласование. Получим структуру, показанную на рис. 4.12.
F(p)
4
– W3W4
(p)
1
Wпрямой_цепи
Рис. 4.12. Структура САУ для вычисления передаточной функции
по каналу «возмущение – рассогласование»
Передаточная функция по каналу «возмущающее воздействие g(t) –
рассогласование (t)» вычисляется по формуле:
1
.
(4.8)
W fy ( p)  W3 ·W4 ·
1  W1 ·W2  W4 ·(1  W1 ·W2 ·W3 )  W5
Решение примера завершено.
3. О пользе передаточных функций для исследования САУ
1. Общая передаточная функция САУ позволяет заключить, является ли САУ устойчивой. Как мы узнаем дальше, для этого нужно найти
корни знаменателя передаточной функции или, по крайней мере, определить, является ли действительная часть каждого корня отрицательной (не
обязательно знать конкретные числовые значения корней). САУ устойчива, если действительные части всех корней знаменателя общей передаточной функции отрицательны (это необходимое и достаточное условие устойчивости).
2. Для устойчивой САУ по общей передаточной функции можно
определить, какое значение будет иметь выход передаточной функции
54
при t  , если на вход поступает постоянное во времени входное воздействие. Для этого в формуле для передаточной функции нужно положить p = 0.
3. Для устойчивой САУ по общей передаточной функции можно
определить, как будет отслеживаться переменное во времени непрерывно
дифференцируемое входное воздействие «на бесконечности», т. е. спустя
промежуток времени, в течение которого ощущается влияние начальных
условий. Данная задача относится к области исследования качества
управления.
4. Контрольные вопросы
Что такое многоконтурная система без перекрестных связей?
Что такое многоконтурная система с перекрестными связями?
Какова технология расчета общей передаточной функции САУ?
Как на структурных схемах САУ обозначаются звено сравнения,
сумматор, узел (развилка)?
5. Как рассчитать передаточную функцию последовательно соединенных звеньев (если передаточная функция каждого звена известна)?
6. Как рассчитать передаточную функцию параллельно соединенных
звеньев (если передаточная функция каждого звена известна)?
7. Как переносится сумматор по ходу и против хода сигнала при
структурных преобразованиях САУ?
8. Как переносится узел (развилка) по ходу и против хода сигнала
при структурных преобразованиях САУ?
9. Как переставляются узлы и сумматоры при структурных преобразованиях САУ?
10. В чем заключается принцип суперпозиции, используемый при
составлении общей передаточной функции по одному из каналов
САУ?
11. Сформулируйте необходимое и достаточное условие устойчивости САУ.
1.
2.
3.
4.
55
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 5
ТЕМА: «КЛАССИФИКАЦИЯ ЗАКОНОВ УПРАВЛЕНИЯ.
ЛИНЕЙНЫЕ ЗАКОНЫ УПРАВЛЕНИЯ.
ПРОПОРЦИОНАЛЬНЫЙ РЕГУЛЯТОР»
Время проведения практического занятия (аудиторные часы) – 2 часа, занятие должно проводиться с компьютерным сопровождением в связи с обширностью материала.
Время самостоятельной работы студента (дополнительные часы) – 2 часа.
Цель занятия: изучить типовой линейный закон управления – пропорциональный (П), получить представление о базовых свойствах САУ с
регулятором этого вида.
Рассматриваемые вопросы:
1. Классификация законов управления.
2. Типовой пропорциональный закон управления и его свойства.
1. Классификация законов управления
Классификация законов управления приведена на рис. 5.1.
Определение 1. Линейным законом управления называется такой, в
котором значение управляющего воздействия является линейной функцией переменных состояния объекта и операторов дифференцирования
и / или интегрирования переменных состояния.
Определение 2. Непрерывным законом управления называется такой, в котором управляющий сигнал является непрерывной функцией
времени.
Определение 3. Цифровым законом управления называется такой, в
котором управляющее воздействие сформировано в реальном времени
цифровым устройством, работающим в дискретном времени и имеющим
ограниченное число разрядов.
Определение 4. Типовыми называются законы управления, встроенные в регуляторы, производство которых осуществляется в промышленных масштабах. Популярность таких законов основана на инженерной
практике.
Определение 5. Специальными называются законы управления,
спроектированные индивидуально для использования в системах автоматизации таких объектов, для которых применение типовых законов
управления не позволяет достичь требуемых значений показателей качества управления.
56
Законы управления
Линейные
Нелинейные
Специальные
Типовые
Непрерывные
Непрерывные
Цифровые
Цифровые
Специальные
Непрерывные
Цифровые
Рис. 5.1. Классификация законов управления
2. Линейные законы управления
Замечание. Материал раздела излагается в форме ответов на тройку вопросов (зачем?  почему?  как?), которую именно в такой последовательности должен задавать
себе каждый инженер при выполнении любой работы. Если инженер точно знает зачем и
понимает, почему не получается нужный ему результат, то опыт показывает, что он почти
всегда изобретет или найдет решение, позволяющее ответить на вопрос как? Добавим, что
отрицательный ответ на первый (второй) вопрос снимает необходимость размышлять над
вторым (третьим) вопросом, и инженер не будет тратить время на решение бессмысленных задач.
2.1. Вводные замечания
Следуя логике инженера (поиск ответов на триаду вопросов зачем?  почему?  как?), зададим себе сначала вопрос: «Зачем вводить
систему управления в добавление к технологическому объекту?». Ответ
очевиден: без системы управления выход объекта может недопустимо
отклониться от задания (например, из-за действия возмущающих факторов – внешних или внутренних, параметрических).
Ответ на второй вопрос: «Почему нельзя устранить несоответствие
выхода задающему воздействию без контура обратной связи, т. е. без регулятора?» – также почти очевиден. Если бы возмущения были пренебрежимо малыми или если бы мы имели возможность их измерять, то
можно было бы обойтись и без обратной связи (использовать более простую разомкнутую систему, если возмущения малы, либо применить более быстродействующую систему, основанную на компенсации возму57
щений, если возмущения существенны). Но мы знаем, что во многих случаях возмущения недоступны для непосредственного измерения (либо по
причине отсутствия соответствующих устройств, либо из-за их высокой
стоимости). В этом случае системе с обратной связью нет альтернативы.
Перейдем к поиску ответа на вопрос как? Существуют различные
технологии этого поиска. Например, можно попытаться поставить задачу
нахождения наилучшего (с позиций критерия, заданного пользователем)
алгоритма управления. Пример такой технологии мы рассмотрим на
практическом занятии, посвященном нелинейным алгоритмам управления. Здесь отметим только, что данная технология сложна и плохо типизируется (в результате не удается перейти от индивидуального проектирования алгоритма управления к типовым алгоритмам, встраиваемым в
регуляторы, выпускаемые промышленностью).
Вторая технология (гораздо более простая) приводит к получению
типовых решений (но, конечно, решение может сильно проиграть в качестве управления по сравнению с разработкой индивидуального проекта
по первой технологии). Эта технология состоит в изобретении алгоритма
и в последующем анализе его свойств.
Используем эту технологию и мы.
Рабочим инструментом такой технологии является перебор претендентов на решение, начиная с простейшего варианта. Подход основан
на знаменитой максиме философа XIII века, получившей в его честь
название «бритва Оккама»: не умножай сущности сложностью. В применении к нашей задаче ее трактовка такова: будем искать решение задачи воспроизведения задающих воздействий на фоне внешних и внутренних возмущений, начиная с простейшего варианта. Затем, анализируя
его, выявим недостатки и будем постепенно усложнять закон управления.
Рассмотрим произвольный регулятор (или контроллер, реализующий
некоторый алгоритм управления), рис. 5.2. Обозначим (t) = g(t) – y(t) –
рассогласование между задающим воздействием g(t) и выходом объекта
y(t). Мы видим, что входом в регулятор является рассогласование, а выходом – управляющее воздействие u(t).
(t) = g(t) – y(t)
Рассогласование
Регулятор
(«закон управления»)
u(t)
Управляющее
воздействие
Рис. 5.2. Вход и выход регулятора в структуре САУ
Понятно, что функцией регулятора является преобразование входного сигнала (рассогласования (t) = g(t) – y(t)) в управляющее воздействие
u(t). Следуя «бритве Оккама», зададим себе вопрос: какая из известных
58
нам функций является простейшей? Ответ очевиден – линейная. С нее и
начнем: попытаемся использовать эту простейшую функцию для генерации законов управления.
2.2. Общая форма линейных законов управления
Общая форма линейного закона управления:
t
t
d
d 2
u (t )  k p · (t )  ki1·  ( )d  ki 2 ·  ( ( )d )d    k d1·  k d 2 · 2   ,(5.1)
0
dt
00
dt
где kp, ki1, ki2, kd1, kd2 – настроечные параметры закона, позволяющие
изменять и настраивать качество управления (соответственно – при пропорциональной, интегральных и дифференциальных составляющих).
Далее, следуя «бритве Оккама», выберем самый простой из линейных законов (5.1). Понятно, что простейшим вариантом является частный
случай (5.1), в котором отсутствуют слагаемые с интегралами и производными.
Поставим задачу исследования свойств системы, оборудованной самым простым вариантом регулятора, получившего название пропорциональный (П-) регулятор.
3. Кривая разгона П-регулятора
Из (5.1) (при отсутствии слагаемых с интегральными и дифференциальными составляющими) следует П-закон управления и соответствующая ему передаточная функция П-регулятора WП(p):
(5.2)
u (t )  k p · (t ), WП ( p)  k p .
С позиций классификации элементарных звеньев П-регулятор представляет собой безынерционное звено (простейшее в перечне элементарных звеньев).
Регулятор включается последовательно с объектом. Структурная
схема САУ с регулятором приведена на рис. 5.3. Для простоты дальнейших выкладок будем полагать, что возмущающее воздействие f(t) методами структурных преобразований приведено ко входу объекта, поэтому
передается на выход по тому же каналу и с той же передаточной функцией, что и задающее воздействие g(t).
Входом в регулятор служит рассогласование (t) = g(t) – y(t) между задающим воздействием g(t) и выходом объекта y(t). Кривые разгона, соответствующие различным настроечным параметрам kp представлены на рис.
5.4 (кривая разгона, согласно ее определению, является реакцией на постоянное воздействие, поступающее на вход; в данном случае представим
себе испытательный стенд с регулятором, на котором на вход регулятора
подается ступенчатый сигнал).
59
Задающее
воздействие
g(t)
Управляющее
воздействие
П-регулятор
u(t)
Выход
Объект
y(t)
Wо(p)
Wp(p) = kp
(t) = g(t) – y(t)
Возмущающее
воздействие f(t)
Рассогласование
Рис. 5.3. Структура САУ с П-регулятором
Выход –
Вход –
рассогласование управляющее
воздействие u(t )
 (t)
k "p  k 'p
k 'p
Время t
Время t
Рис. 5.4. Кривые разгона П-регулятора
4. Исследование свойств системы управления с П-регулятором
Следуя логике «зачем? почему? как?», зададим себе вопрос: «А
зачем исследовать свойства системы управления с регулятором определенного вида?» Ответ состоит в том, что обнаруженные достоинства помогут определить область применения регулятора, а недостатки послужат стимулом для поиска решений, направленных на их устранение.
Цели исследований свойств системы с П-регулятором – выяснить:
1. Насколько точно воспроизводит система с П-регулятором постоянное задающее воздействие?
2. Насколько выше качество управления в системе с П-регулятором
(по сравнению с разомкнутой системой)?
3. Понижается или повышается чувствительность системы с Прегулятором к неизбежным неточностям сведений о параметрах
объекта (по сравнению с разомкнутой системой)?
60
Исследования и ответы на поставленные вопросы
Обозначим передаточную функцию объекта Wo(p) и будем считать,
что она имеет следующую форму:
ko
,
(5.3)
Wo ( p) 
Q( p )  1
где Q(p) – полином заданной степени оператора Лапласа p;
ko – коэффициент усиления объекта.
Примечание: такая форма очень типична и на практике встречается чаще всего;
например, такую форму мы встречали при описании объекта нагрева, см. практическое занятие 1, формулы (1.1) и (1.8), для которых Q(p) является полиномом 1-го и 2-го порядков
соответственно.
Дальнейшие выкладки проведем по следующей схеме, типичной для
анализа САУ:
Шаг 1. Составим общую передаточную функцию замкнутой САУ.
Шаг 2. По ней получим описание работы САУ в пространстве оператора Лапласа.
Шаг 3. Считая, что на вход САУ поступают постоянные во времени
воздействия (задающее g(t) = g = const и возмущающее f(t) = f = const),
найдем значение выхода САУ в статике (используя двойственность,
«зеркальность» переменных время и оператор Лапласа). Для этого положим p = 0 (что и будет соответствовать статике, t  ∞).
Шаг 4. Сравним выход САУ с заданием и установим, имеет ли место
статическая ошибка по каждому из каналов (по каналам g(t)  y(t) и
f(t)  y(t) передачи задающего и возмущающего воздействий на выход
соответственно).
Шаг 5. Если обнаружим, что статическая ошибка имеет место, то
постараемся найти прием для ее устранения. Посмотрим, можно ли обеспечить отсутствие статической ошибки по каждому из каналов.
Шаг 6. Рассчитаем по такой же схеме статическое значение выхода
объекта в разомкнутой системе, т. е. такой, в которой регулятора нет.
Шаг 7. Предположим, что значение коэффициента усиления ko отклоняется от принятого в расчетах (из-за неизбежных ошибок идентификации) на величину Δko, и проанализируем, в какой системе (с регулятором или в разомкнутой) эта неточность сильнее влияет на величину отклонения выхода от задания. Сделаем вывод о чувствительности САУ по
отношению к неточностям определения коэффициента усиления объекта.
4.1. Выполнение шага 1: составление общей передаточной
функции замкнутой САУ
Используя теорему 3 алгебры структурных преобразований (о передаточной функции САУ, охваченной отрицательной обратной связью),
61
получим (полагая, как отмечалось выше, что возмущение приведено ко
входу объекта):
k p ·k o
k p ·k o
Q( p)  1
по каналу g (t )  y(t ) , (5.4)
Wgy ( p ) 

k p ·k o
Q ( p )  1  k p ·k o
1
Q( p)  1
ko
ko
по каналу f (t )  y(t ) . (5.5)
Q( p)  1
W fy ( p) 

k p ·ko
Q( p)  1  k p ·ko
1
Q( p)  1
4.2. Выполнение шага 2: получение описания работы САУ в пространстве оператора Лапласа
Используя формулу для передаточной функции и принцип суперпозиции (реакция линейной САУ на сумму входных воздействий равна
сумме реакций САУ на каждое воздействие в отдельности), получим модель «вход–выход» в пространстве оператора Лапласа:
(5.6)
Y ( p)  Wgy ( p)·G ( p)  W fy ( p)·F ( p) ,
где G(p), F(p) – соответственно изображения по Лапласу задающего g(t)
и возмущающего f(t) воздействий.
В рассматриваемом случае входные воздействия постоянны, поэтому, согласно свойству преобразования Лапласа, G(p) = g = const,
F(p) = f = const.
Используя (5.6), (5.4) и (5.5), получим:
k p ·ko
ko
(5.7)
Y ( p) 
·g 
·f .
Q( p)  1  k p ·ko
Q( p)  1  k p ·ko
4.3. Выполнение шага 3: определение значение выхода САУ ystatic
в статике
Для этого в (5.7) нужно положить p = 0 (это соответствует t  ∞).
Все степени p в Q(p) превратятся в нули, поэтому:
y static 
k o ·k p
1  k o ·k p
·g 
ko
·f .
1  k o ·k p
(5.8)
4.4. Выполнение шага 4: сравнение выхода с заданием в статике,
проверка наличия статической ошибки: static = g – ystatic = 0?
Из (5.8) видно, что выход объекта отличается от задания, и это
отличие тем меньше, чем больше коэффициент усиления регулятора
(словами инженера – чем глубже обратная связь).
62
В пределе при бесконечно большом параметре регулятора (kp ∞)
получается, что статический режим точно соответствует заданию, несмотря на наличие возмущений:




ko
 ko

(5.9)
lim y static  lim 
·g 
·f   g .
k p 
k p  1
1

k
·
k
o
p
 ko


 kp

Казалось бы, чем больше параметр kp, тем лучше качество управления.
Но, к сожалению, kp влияет не только на статику, но и на динамику процесса. На рис. 5.5а показаны графики отработки ступенчатого изменения задающего воздействия (возмущений нет) при двух значениях kp. Мы видим,
что статическая ошибка для процесса с большим kp меньше. Но другие показатели качества управления (колебательность и перерегулирование)
ухудшились. При недопустимо большом kp статический режим вообще не
достигается, а динамика становится неустойчивой (рис. 5.5б).
Задающее воздействие
Задающее воздействие
Выход САУ при kp = 2.5
Выход САУ при kp = 1
Выход САУ при kp = 5
а) статическая ошибка уменьшается,
колебательность увеличивается
б) при недопустимо большом значении
kp САУ теряет устойчивость
Рис. 5.5. Иллюстрация влияния увеличения параметра kp П-регулятора на качество
отработки задания (возмущение отсутствует)
Аналогичные выводы можно сделать и при рассмотрении качества
подавления возмущений. Мы видим (рис. 5.6), что чем больше kp, тем
меньше проявляется влияние возмущения на статическое значение выхода, но тем сильнее выражаются явления колебательности, увеличивается перерегулирование и при недопустимо большом значении kp наступает
неустойчивость.
63
Выход САУ при kp = 5
Выход САУ
при kp = 2.5
Выход САУ при kp = 1
Возмущающее воздействие
Возмущающее воздействие
а) статическая ошибка уменьшается, колебательность увеличивается
б) при недопустимо большом значении
kp САУ теряет устойчивость
Рис. 5.6. Иллюстрация влияния увеличения параметра kp П-регулятора на качество
подавления возмущения (задающее воздействие – нулевое)
Замечания:
1. Нужно обратить внимание на необходимость выбора настроечного параметра регулятора kp, исходя из компромисса между качеством статического режима и качеством динамики. Например, при завышенном kp (даже для устойчивого управления) могут произойти нарушения технологического режима, если перерегулирование будет недопустимо
большим.
2. Также нужно подчеркнуть возможность определения kp, при котором достигается
наибольшее быстродействие системы (минимум времени переходного процесса). Если kp
слишком мал, перерегулирование будет небольшим, но процесс достижения статики будет
вялым и время переходного процесса (т. е. время, в течение которого статический режим
будет достигнут с заранее заданной точностью, см. рис. 3.10а) будет большим. Если kp
слишком высок (но САУ устойчива), то начальный участок динамического процесса будет
«резвым» (рис. 5.5а), но время переходного процесса окажется снова большим из-за колебаний выхода, не укладывающихся в трубку статики. Если построить зависимость времени
переходного процесса от значения kp, то мы обнаружим наличие минимума. Таким образом,
вводится понятие оптимальной настройки параметров регулятора. Критериев настройки
может быть много. Для систем управления, целью которых является стабилизация выхода
объекта, естественным критерием является время переходного процесса (возможно, при
ограничениях на величину перерегулирования).
Отметим, что зависимость времени переходного процесса от kp не во всей области изменения kp является выпуклой и неразрывной. Возможно существование зоны, в которой
малые изменения kp приводят к значительным изменениям времени переходного процесса
(рис. 5.7). Причину этого поясняет рис. 5.8.
Рис. 5.7. Характер зависимости времени переходного процесса от значения настроечного
параметра П-регулятора
64
а) трубка статики охватывает весь интервал
перерегулирования
б) интервал перерегулирования не укладывается в трубку статики
Рис. 5.8. Резкое изменение времени переходного процесса при небольших изменениях
настроечного параметра П-регулятора kp
Мы видим, что при kp = 0.37 (рис. 5.8а) вход в трубку статики происходит при первом,
«верхнем» пересечении границы трубки, поэтому часть процесса изменения выхода объекта, имеющая перерегулирование, укладывается внутри трубки. При изменении параметра
настройки всего на 5 % (kp = 0.39, рис. 5.8б) картина существенно иная: вход в трубку статики происходит на втором, «нижнем» пересечении границы трубки, поэтому время переходного процесса увеличивается сразу на 10 % (т. е. коэффициент чувствительности времени переходного процесса к изменению настроечного параметра
kчув ств 
t process регуляk p
тора равен 2; здесь Δtprocess – приращение времени переходного процесса, соответствующее
изменению настроечного параметра kp на величину Δkp). Значение kp, соответствующее
«перескоку» от одной границы трубки статики к другой, приводит к разрыву (первого рода)
зависимости времени переходного процесса от значения kp.
При дальнейшем изменении kp также возможны нарушения выпуклости из-за колебаний значений выхода вокруг статического значения (возможны «перескоки» между границами трубки статики при небольших изменениях настроечного параметра kp).
Наличие разрывов в зависимости времени переходного процесса от kp затрудняет постановку задачи определения наилучшего значения настроечного параметра: если ориентироваться на минимальное время переходного процесса, то в процессе работы регулятора изза неизбежных изменений параметров объекта реальное быстродействие системы может
оказаться значительно больше минимально возможного. Отсюда следует, что настроечный
параметр целесообразно выбрать не в оптимуме, а левее оптимума (с запасом на возможные
изменения параметров объекта), т. е. намеренно занизить значение настроечного параметра
регулятора. Проигрыш, как показывает рис. 5.7, не будет слишком велик: на участке непрерывности левее оптимума небольшие изменения параметра kp не вызывают больших изменений времени переходного процесса. Альтернативой намеренного занижения значения
настроечного параметра является введение механизма непрерывной адаптации системы в
процессе ее функционирования.
65
4.5. Выполнение шага 5: нахождение приема, позволяющего устранить статическую ошибку в воспроизведении задающего воздействия
Возвратимся к формуле (5.8) и рассмотрим ее частный случай: работу системы управления, в которой отсутствуют возмущения, f = 0. В этом
случае статическое значение выхода ystatic не соответствует заданию, имеет место статическая ошибка:
ko · k p
(5.10)
· g  g.
1  ko · k p
Но мы видим, что объект можно «обмануть», предложив ему вместо
y static 
1 k o · k p
задающего воздействия значение g
· g . Тогда статичеcorrect 
ko · k p
ское значение выхода объекта будет точно соответствовать заданию g:
k ·k
k ·k 1  ko ·k p
(5.11)
ystatic  o p ·g correct  o p ·
·g  g .
1  ko ·k p
1  ko ·k p ko ·k p
Мы получили полезный инженерный прием: подавать задающее воздействие на элемент сравнения не непосредственно, а через безынерционное звено (усилитель) с передаточной функцией (коэффициентом уси1 k o · k p
ления): k 
.
corr
ko · k p
Получим структурную схему (рис. 5.9), в которой САУ с Прегулятором не имеет статической ошибки воспроизведения задающего
воздействия.
Задающее воздействие
Корректирующее
звено kcorr
g(t)
Управляющее
воздействие
Выход
u(t)
y(t)
П-регулятор
Объект
Wо(p)
Wp(p) = kp
f(t)
Возмущающее
воздействие
Рис. 5.9. Структура САУ с П-регулятором и корректирующим звеном
Замечание. Этот пример может служить иллюстрацией полезности схемы рассуждений, состоящей в поиске последовательных ответов на тройку вопросов «зачем?  почему?  как?».
Зачем? Чтобы попытаться устранить статическую ошибку.
66
Почему она имеет место? Потому что на вход объекта подается не задающее воздействие, а его значение, умноженное на коэффициент
ko ·k p
1  ko ·k p
, см. (5.11).
Как устранить ошибку? Ответ очевиден: подать на вход звена сравнения «обманное»
задающее воздействие; для этого исходное задающее воздействие нужно подать через уси-
1 ko ·k p .
ko ·k p
Теперь посмотрим, поможет ли тот же прием для устранения статической ошибки, связанной с подавлением неизмеряемого возмущения.
Для этого проанализируем частный случай формулы (5.8), в котором задающее воздействие g = 0:
ko
(5.12)
ystatic 
·f  0 .
1  ko ·k p
Мы видим, что полное подавление возмущающего воздействия в системе с П-регулятором невозможно (достигается только при kp ∞, а
это, как мы уже отмечали, ведет к неустойчивости). Инженер, обнаруживший это, найдёт ответы на вопросы зачем? и почему? и станет искать
ответ на вопрос как? путем замены закона управления, реализуемого регулятором.
литель с коэффициентом
kcorr 
Примечание: если возмущение можно измерить, то лучше вместо структуры с обратной связью использовать структуру с другим принципом организации – структуру с компенсацией возмущения.
Итак, запомним, что в САУ с П-регулятором:
1. Статическая ошибка воспроизведения постоянного задающего
воздействия может быть устранена путем ввода корректирующего
усилителя в структуру САУ.
2. Статическая ошибка, возникающая из-за действия возмущений,
принципиально неустранима. Естественно, такое свойство может
оказаться неприемлемым для систем, в которых требуется высокая
точность воспроизведения задающих воздействий.
4.6. Выполнение этапа 6: расчет статического значения выхода
объекта в разомкнутой системе
Цель выполнения этапа (ответ на вопрос зачем?) – получить базу
для сравнения: ведь если окажется, что в системе без регулятора качество
управления лучше, чем в системе с обратной связью – то зачем применять систему с регулятором? Структура разомкнутой системы показана
на рис. 5.10. Для простоты рассмотрим случай, когда возмущения нет, а
на вход объекта подается постоянное задающее воздействие gраз(t).
67
Возмущающее
воздействие
f(t)
Выход
Задающее воздействие
Объект
gраз(t)
Wо(p)
Yраз(t)
Рис. 5.10. Структура разомкнутой САУ
В этом случае изображение выхода Yраз(p) объекта разомкнутой САУ
имеет вид:
ko
(5.13)
Yраз ( p)  Wo ( p)·G раз ( p) 
·g раз .
Q( p )  1
Величину gраз(t) выберем из условия, чтобы в статике выход объекта
был равен заданию (такому же, как в замкнутой САУ, т. е. g). Статический режим (t  ∞) соответствует значению оператора Лапласа p = 0.
Получим:
ko
y раз _ статич 
·g раз  ko ·g раз должно быть  g .
Q( p)  1 з0
Отсюда
1
(5.14)
g раз  ·g .
ko
Мы видим, что статический режим можно обеспечить без ошибки
(конечно, если мы точно знаем коэффициент усиления объекта ko). Зачем
же тогда обратная связь? Мы уже отвечали на этот вопрос на практическом занятии № 3: а) для подавления внешних возмущений; б) для подавления внутренних, параметрических, возмущений; в) для ускорения динамики перехода с одного статического режима на другой.
Примечание: полезно обратиться к рис. 3.7, 3.8, 3.9, приведенным в описании практического занятия № 3.
4.7. Выполнение шага 7: сравнение чувствительности разомкнутой системы с чувствительностью системы с П-регулятором по отношению к коэффициенту усиления объекта
Как мы только что отметили, см. (5.14), достижение требуемого значения выхода объекта базируется в разомкнутой системе на точных сведениях о коэффициенте усиления объекта ko.
Определение параметра корректирующего усилителя (уничтожающего статическую ошибку воспроизведения задания) для системы с
68
П-регулятором также требует, чтобы коэффициент усиления объекта ko
был известен точно.
Но на практике этот параметр практически никогда не может быть
известен точно (в частности, потому что он определяется по экспериментальным данным, подверженным искажениям и погрешностям). Поэтому точное воспроизведение задающего воздействия и в замкнутой, и в
разомкнутой системе недостижимо.
Постановка вопроса зачем? Нужно проверить, насколько чувствительно значение выхода объекта к его коэффициенту усиления ko в разомкнутой САУ и в системе с обратной связью. Если окажется, что последняя более чувствительна, чем разомкнутая, то это будет контраргументом
против практичности системы с обратной связью.
Ответ на вопрос: «Почему требуется такое исследование?» – очевиден: без оценки влияния неизбежных неточностей в определении коэффициента усиления объекта ko нельзя заключить: а) насколько эффективна мера, состоящая во введении корректирующего усилителя в структуру
с П-регулятором; б) ослабляет или (наоборот) подчеркивает обратная
связь влияние неточностей определения ko на качество воспроизведения
задания по сравнению с разомкнутой системой.
Ответ на вопрос как? строится по следующей схеме:
1. Предполагаем, что значение коэффициента усиления объекта ko
известно с точностью до погрешности Δko, а расчеты задающего воздействия gраз для разомкнутой системы и корректирующего коэффициента
1 ko ·k p проведем в предположении, что коэффициент усиления
kcorr 
ko ·k p
объекта равен ko.
2. Рассчитываем, чему равно значение выхода объекта в статике ystatic
в зависимости от величины погрешности Δko определения ko, для разомкнутой системы и для САУ с П-регулятором.
3. Сравниваем результаты и делаем выводы.
Выполнение схемы:
1. Зависимость статического значения выхода объекта от погрешности Δko определения коэффициента усиления объекта ko рассчитаем для
разомкнутой системы так:
1
(5.15)
y раз _ статич (ko )  (ko  ko )· ·g .
ko
Переходя к относительной погрешности Δko/ko определения коэффициента усиления ko объекта, получим:
y раз _ статич ko
,
(5.16)

g
ko
69
где Δyраз_статич = yраз_статич – g – абсолютная ошибка воспроизведения задающего воздействия в разомкнутой системе.
Из (5.16) мы видим, что на один процент неточности сведений о коэффициенте усиления объекта ko приходится один процент отклонения
выхода от задания (коэффициент чувствительности выхода объекта к
отклонению фактического значения ko от принятого в расчете задающего
воздействия для разомкнутой системы равен единице).
Результат расчета показывает, что добиться высокой точности воспроизведения задания в разомкнутой системе трудно: обычно коэффициент усиления объекта известен с погрешностью порядка 10 – 15 %; во
многих системах 10 – 15 %-ная погрешность воспроизведения задания
недопустима (хотя, конечно, есть примеры, особенно в бытовых приборах, когда и такая погрешность не опасна).
2. Аналогичную зависимость для САУ с П-регулятором рассчитаем
так:
(ko  ko )·k p 1  ko ·k p
(5.17)
ystatic(ko ) 
·
·g .
1  (ko  ko )·k p ko ·k p
Переходя к относительной погрешности Δko/ko, получим:
,
(5.18)
ystatic ko
1
g

·
ko   (  1)·ko
ko
где  = 1+ ko∙kp, Δystatic = ystatic – g.
Мы видим, что относительная ошибка (5.18) воспроизведения выхода объекта в САУ с П-регулятором отличается от относительной ошибки
(5.16) в разомкнутой САУ коэффициентом
(5.19)
1
,
h(k p , ko ) 
ko
  (  1)·
ko
т. е.
y static y раз _ статич
(5.20)

·h(k p , k o ) .
g
g
Значение коэффициента h(kp, Δko) зависит от настроечного параметра kp регулятора (через формулу для ) и от относительной погрешности
оценки коэффициента усиления Δko/ko.
3. Вывод о том, меньше или больше чувствительность САУ с Прегулятором к погрешностям оценки коэффициента усиления объекта по
сравнению с чувствительностью разомкнутой системы, зависит от того,
является ли коэффициент h(kp, Δko) меньше или больше единицы (см.
(5.20)). Если окажется, что h(kp, Δko) меньше единицы, то вывод будет в
70
пользу САУ с П-регулятором: относительная ошибка при одной и той же
величине погрешности определения коэффициента усиления объекта в
САУ с П-регулятором будет меньше, чем в разомкнутой системе.
Проанализируем соотношение между h(kp, Δko) и единицей. Предположим, что знаки расчетных значений коэффициента усиления объекта и
настроечного параметра регулятора совпадают (как и требуется для того,
чтобы система управления гарантированно была устойчива). Не ограничивая общности, будем полагать, что оба коэффициента положительны,
ko > 0, kp > 0, поэтому  = 1 + ko ∙ kp > 0. Могут иметь место следующие
варианты:
Ситуация 1. Пусть фактическое значение коэффициента усиления
объекта не меньше расчетного, т. е. пусть Δko  0.
Тогда (  1)·ko  (1  ko ·k p  1)·ko  k p ·ko  0 .
ko
ko
ko
Поэтому знаменатель в (5.19) окажется больше единицы:
k
[  (  1)· o ]    1 , а коэффициент h(kp, Δko) (согласно 5.19) – меньko
ше единицы.
Таким образом, если фактическое значение коэффициента усиления
объекта не меньше расчетного, то вывод – в пользу САУ с П-регулятором: в системе с обратной связью меньше чувствуются погрешности
определения коэффициента усиления объекта.
Ситуация 2. Пусть фактическое значение коэффициента усиления
объекта меньше расчетного, но фактическое значение коэффициента усиления (как и расчетное) положительно (трудно вообразить себе ситуацию,
когда разработчик системы управления будет настолько неграмотен, что
ошибется в знаке коэффициента усиления), т. е. пусть -1 < Δko/ko  0. Тогда знаменатель в (5.19) рассчитаем так:

k o
k o
k o
k o
   (1   )·
 1  k o ·k p  k o ·k p ·
 1  k o ·k p ·1 
ko
ko
ko
ko

  (  1)·
.



ko
 1 , то и в этом случае получилось,
ko
ko
 [1  (число  0)]  1 ,
что знаменатель (5.19) больше единицы:   (  1)·
ko
а коэффициент h(kp, Δko) (согласно 5.19) меньше единицы.
Таким образом, и в том случае, когда фактическое значение коэффициента усиления объекта меньше расчетного, но погрешность его определения менее 100 %, то вывод также в пользу САУ с П-регулятором: в
Поскольку мы полагали, что
71
системе с обратной связью меньше чувствуются погрешности определения коэффициента усиления объекта.
Примечание. Ситуация, при которой погрешность определения коэффициента усиления настолько велика, что знаки расчетного и фактического значений не совпадают, требует
особого анализа (хотя на практике такая ситуация почти не встречается). В частности, если
Δko < 0 и
ko 1  ko ·k p , знаменатель (5.19) обращается в нуль и относительная по
ko
ko ·k p
грешность воспроизведения выхода объекта стремится к бесконечности. Это пример границы устойчивости 3-го вида. При других значениях |Δko| /ko в диапазоне Δko/ko < -1 (т. е. при
погрешности в определении коэффициента усиления объекта более 100 %) чувствительность САУ с П-регулятором проигрывает чувствительности разомкнутой САУ.
На рис. 5.11 показаны зависимости относительной погрешности воспроизведения задающего воздействия от относительной погрешности
определения коэффициента усиления объекта. Мы видим следующее:
1. При одной и той же погрешности определения ko погрешность
воспроизведения задающего воздействия в САУ с П-регулятором
меньше, чем в разомкнутой САУ.
2. Различия в пользу САУ с П-регулятором тем больше, чем больше
величина настроечного параметра kp.
3. В практическом диапазоне погрешностей определения коэффициента усиления объекта ( 20 %) относительная погрешность
воспроизведения задания укладывается в узкий диапазон ( 5 %)
при рабочих значениях настроечного параметра kp.
4. Для практики лучше занизить предположение о величине коэффициента усиления объекта, см. графики в первом квадранте рис.
5.11.
Замечание. Возможно, следует пояснить, почему же (по какой физической причине)
обратная связь в САУ с П-регулятором не может устранить статическую ошибку. Ведь обратная связь предназначена именно для того, чтобы ее устранить. Пояснение – по рис. 5.12.
С одной стороны, статическое значение ystatic выхода объекта связано со статическим
значением рассогласования static = g – ystatic соотношением ystatic = g – static. В координатах
«рассогласование–выход» эта зависимость имеет форму обратной линейной, пересекающей
координатную плоскость под углом 45. С другой стороны, рассогласование является входом участка последовательного соединения регулятора и объекта, см. рис. 5.3. Поэтому статическое значение выхода определяется еще одним соотношением ystatic = ko ∙ kp ∙ static. Если
задать значения ko, kp, то эта зависимость имеет форму прямой линейной, исходящей из
начала координат. При разных значениях настроечного параметра регулятора kp угол
наклона этой прямой к оси абсцисс будет тем больше, чем больше kp.
Точка равновесия определяется пересечением прямых ystatic = g – static и ystatic = ko∙kp∙static.
Мы видим, что при заданных значениях ko, kp статическая ошибка неизбежна, и она тем
меньше, чем больше настроечный параметр П-регулятора kp.
72
Рис. 5.11. Неточности в определении коэффициента усиления объекта МЕНЬШЕ
сказываются на точности воспроизведения задающего воздействия в САУ с
П-регулятором (по сравнению с разомкнутой системой)
1 – прямая ystatic(static) = g – static; 2 – прямая ystatic(static) = ko · kp · static при kp = 0.8;
3 – прямая ystatic(static) = ko · kp · static при kp = 2.5.
Рис. 5.12. Пояснения к причине наличия статической ошибки в САУ с П-регулятором
73
5. Сводка свойств системы управления с П-регулятором
Исследования, описанные в п. 4, позволяют сделать следующие выводы.
САУ с П-регулятором свойственны:
1. Принципиальное наличие статической ошибки: lim  (t )  0 .
t 
2. Возможность устранения статической ошибки по каналу «задающее воздействие – выход объекта», невозможность устранения статической ошибки по каналу «возмущающее воздействие –
выход объекта».
3. Понижение чувствительности САУ к неточностям сведений о
коэффициенте усиления объекта (по сравнению с разомкнутой
системой).
Кроме того, имеют место следующие свойства (очевидные, не нуждающиеся в пояснениях):
1. Простота структуры (П-регулятор имеет простейшую передаточную функцию).
2. Простота настройки параметра (имеет единственный настраиваемый параметр kp).
3. Высокое быстродействие реакции на появление рассогласования
(П-регулятор – безынерционное звено).
4. Простота обеспечения требований к устойчивости (П-регулятор
как безынерционное звено не увеличивает порядок знаменателя
передаточной функции САУ).
6. Контрольные вопросы
Как классифицируются законы управления?
Какой закон управления называется линейным?
Какой закон управления называется непрерывным?
Какой закон управления называется цифровым?
Какие законы управления называются типовыми?
Какие законы управления называются специальными?
Может ли быть устранена статическая ошибка воспроизведения
постоянного задающего воздействия в САУ с П-регулятором?
Если да, то каким образом?
8. Может ли быть устранена статическая ошибка, возникающая изза действия возмущений в САУ с П-регулятором? Если да, то каким образом?
9. Каковы преимущества пропорционального закона управления?
10. Каковы недостатки пропорционального закона управления?
1.
2.
3.
4.
5.
6.
7.
74
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 6
ТЕМА: «ЛИНЕЙНЫЕ ЗАКОНЫ УПРАВЛЕНИЯ.
ПРОПОРЦИОНАЛЬНО-ИНТЕГРАЛЬНЫЙ РЕГУЛЯТОР»
Время проведения практического занятия (аудиторные часы) – 2 часа, занятие должно проводиться с компьютерным сопровождением в связи с обширностью материала.
Время самостоятельной работы студента (дополнительные часы) – 2 часа.
Цель занятия: изучить типовые линейные законы управления – интегральный (И) и пропорционально-интегральный (ПИ), получить представление о базовых свойствах САУ с регуляторами этих видов.
Рассматриваемые вопросы:
1. Интегральная составляющая в законе управления.
2. Типовой интегральный закон управления и его свойства.
3. Типовой пропорционально-интегральный закон управления и его
свойства.
1. Свойства И-регулятора
1.1. Зачем вводить интегральную составляющую в закон управления?
Следуя «закону логики инженера» (зачем?  почему?  как?), ответим сначала на вопрос: «Зачем искать закон управления, если есть экономичный простейший пропорциональный П-регулятор?». Ответ очевиден: в САУ с П-регулятором имеется неустранимая статическая ошибка при отработке неконтролируемых возмущающих воздействий.
Почему возникает эта ошибка, поясняют формула (5.8) и п. 4.7 из
практического занятия № 5.
В рамках структуры с П-регулятором статическую ошибку устранить нельзя, поэтому ответ на вопрос: «Как ее устранить?» нужно искать
в направлении изменения структуры регулятора. Нужно найти такое
звено управляющей системы, которое могло бы «запомнить» и сохранить на выходе регулятора значение управляющего воздействия, при котором рассогласование между задающим воздействием и выходом объекта равно нулю.
Простейший способ попытаться найти ответ на вопрос как? – провести перебор по известным элементам структуры САУ.
Рассмотрим (в качестве претендентов на обладание таким свойством) элементарные звенья. Ответ на вопрос: «Почему именно элементарные?» – в максиме «лезвие Оккама»: решение нужно искать начиная с
простейших вариантов и усложнять варианты только в том случае, когда
перебор простейших вариантов не приведет к успеху.
75
1.2. Можно ли устранить статическую ошибку регулятором, в
качестве которого используется элементарное звено из группы звеньев с самовыравниванием?
Начнем с простейшей, первой группы элементарных звеньев – звеньев с самовыравниванием (рассмотрены в лекционном курсе). Общая
форма передаточной функции этих звеньев:
k зв _ самовыравн
,
W зв _ самовыравн 
Qсамовыравн ( p)  1
где kзв_самовыравн, Qсамовыравн(p) – соответственно коэффициент усиления
звена и полином оператора Лапласа соответствующей размерности. Если
использовать звенья этой группы в качестве регулятора, то передаточная
функция замкнутой САУ объектом, передаточная функция которого
представлена формулой (5.3), получится такой (для канала «задающее
воздействие – выход»):
k зв _ сам ов ырав н
ko
·
Qсам ов ырав н( p )  1 Q( p )  1
W gy ( p ) 

k зв _ сам ов ырав н
ko
1
·
Qсам ов ырав н( p )  1 Q( p )  1

k зв _ сам ов ырав н · k o
Qсам ов ырав н( p ) · Q( p )  Qсам ов ырав н ( p )  Q( p )  (1  k зв _ сам ов ырав н · k o )
(6.1)
Статическое значение выхода объекта ystatic (при t  ∞), соответствующее подаче на вход объекта постоянного задающего воздействия g,
определяется по передаточной функции при p = 0:
ystatic  Wgy ( p )
p 0
·g
k зв _ сам овыравн · ko
1  k зв _ сам овыравн · ko
· g.
(6.2)
Формула (6.2) с точностью до обозначений совпадает с формулой (5.8),
полученной для П-регулятора (для случая, когда возмущение отсутствует).
Следовательно, группа звеньев с самовыравниванием (как и
входящее в эту группу безынерционное звено – П-регулятор) не может устранить статическую ошибку при отработке неконтролируемых возмущающих воздействий.
1.3. Можно ли устранить статическую ошибку регулятором, в
качестве которого используется интегрирующее элементарное звено?
Перейдем к следующей группе элементарных звеньев (интегрирующих) и начнем, следуя «бритве Оккама», с простейшего – идеального интегрирующего звена, передаточная функция которого равна
76
ki .
(6.3)
p
Передаточная функция замкнутой САУ, в которой интегрирующее
звено выполняет роль регулятора (по структурной схеме, аналогичной
рис. 5.3, где П-регулятор заменен интегральным, И-регулятором с передаточной функцией по (6.3)), равна:
1. По каналу «задающее воздействие g(t) – выход объекта y(t)»:
ki
ko
·
Wint ( p)·Wo ( p)
ki ·ko
p Q( p)  1
. (6.4)
Wgy ( p) 


k
k
1  Wint ( p)·Wo ( p) 1  i ·
p·[Q( p)  1]  ki ·ko
o
p Q( p)  1
2. По каналу «возмущающее воздействие f(t) – выход объекта y(t)»:
ko
Wo ( p)
p·ko
Q( p)  1
. (6.5)
W fy ( p) 


k
k
1  Wint ( p)·Wo ( p) 1  i ·
p·[Q( p)  1]  ki ·ko
o
p Q( p)  1
Статическое значение выхода объекта (достигается при t  ∞), если
на вход подается постоянное воздействие g(t) = g = const и f(t) = f = const,
соответствует значению оператора Лапласа, равному нулю. Получим:
1. Если возмущающее воздействие равно нулю:
k ·k
(6.6)
ystatic  Wgy ( p) ·g  i o ·g  g .
p 0
ki ·ko
2. Если задание равно нулю, но на САУ действует возмущение:
0·ko
(6.7)
ystatic  W fy ( p ) ·g 
·f  0 .
p 0
ki ·ko
Формулы (6.6) и (6.7) показывают, что использование И-регулятора
в САУ достигает цели: статическая ошибка в такой САУ отсутствует.
Задающее воздействие в статике в САУ с И-регулятором воспроизводится точно, а постоянные возмущения подавляются до нуля.
Статическая ошибка в САУ с И-регулятором отсутствует.
Wint ( p) 
1.4. Свойства интегрального звена и кривая разгона Ирегулятора
На рис. 6.1 показаны графики отработки ступенчатого задающего
воздействия (рис. 6.1а) и ступенчатого возмущающего воздействия
(рис. 6.1б), иллюстрирующие перечисленные свойства И-регулятора.
77
а) в САУ с И-регулятором задающее возб) в САУ с И-регулятором возмущающее
действие в статике воспроизводится точно
воздействие в статике подавляется до нуля
Рис. 6.1. Иллюстрация свойств интегрального закона управления
Эффект отсутствия статической ошибки объясняется природой интегрирующего звена: если на «вход» интеграла подать постоянное число ,
то выход u(t) будет непрерывно изменяться по линейному (во времени)
t
закону: u (t )   ·dt   ·t . Если в некоторый момент времени t* > t скач
0
ком изменить «вход» до нуля, то интеграл «запомнит» значение, достигнутое в момент t* (не произойдет сброс значения интеграла до нуля):
при t  t * u (t )   ·t
при t  t *  (t )    const

Если 
, то 
при
t

t
*

(
t
)

0
при
t
 t * u (t )   ·t*  const


Получим эффект, нужный для САУ, не имеющей статической ошибки: хотя на входе регулятора – нуль, на выходе поддерживается управляющий сигнал, отличающийся от нуля – именно такой, при котором статическая ошибка отсутствует.
Кривая разгона И-регулятора и его реакция на входной сигнал (рассогласование (t) между задающим воздействием и выходом объекта в форме
прямоугольного продолжительного импульса) показаны на рис. 6.2.
а) вход И-регулятора: рассогласование
б) вход И-регулятора: рассогласование (t) –
 = const
прямоугольный импульс
Рис. 6.2. Кривая разгона И-регулятора и иллюстрация к его свойству запоминать значение
выхода после снятия входного сигнала
78
Примечание. Не нужно думать, что на практике интегрирующие звенья встречаются
редко. Каждый видел счетчик расхода электроэнергии и регистратор километража, пройденного автомобилем: такие устройства не сбрасывают сигнал после остановки. В дискретном времени хорошим аналогом интегратора является домашняя копилка: количество денег
в ней не изменяется до момента вбрасывания новой монетки, и копилка «запоминает»
накопленную сумму.
2. Зачем усложнять структуру И-регулятора? Идея ПИ-регулятора
Цель устранения статической ошибки достигнута путем перехода от
пропорционального к интегральному закону управления. Спрашивается –
зачем искать пути дальнейшего усложнения структуры регулятора?
Ответ: можно догадаться, что платой за достижение полезного эффекта является резкое снижение скорости реакции САУ на появление
рассогласования между заданием и выходом объекта.
Почему это происходит? Причина – в природе процесса интегрирования; вблизи момента появления рассогласования изменения выхода интегрирующего звена очень малы:
t  t
u (t  t )  u (t ) 

· dt  u (t )   · t  u (t ).
t
Должен пройти заметный промежуток времени, пока САУ с И-регулятором «почувствует», что выход отклонился от задания.
Как устранить нежелательный эффект потери скорости реакции и одновременно не потерять полезный эффект устранения статической ошибки? Вспомним, что в САУ с П-регулятором скорость реакции на появление
рассогласования была высокой (управляющее воздействие, пропорциональное рассогласованию, появляется на входе объекта безынерционно).
На рис. 6.3 приведены результаты сравнения переходных процессов
в системах с И-регулятором и с П-регулятором. Иллюстрируются их «инверсные» свойства: высокое быстродействие П-регулятора, сопровождаемое статической ошибкой, и отсутствие статической ошибки в САУ с Ирегулятором, сопровождаемое низким быстродействием.
Сравнение САУ с П- и И-регуляторами подводит нас к ответу на вопрос как?: нужно включить параллельно оба регулятора. Тогда в начальной части процесса П-составляющая обеспечит быструю реакцию на появление рассогласования, а в концевой части процесса И-составляющая
«дотащит» выход объекта до задания. Результаты такого сотрудничества
регуляторов показаны на рис. 6.4. Мы видим, что полезные эффекты сохранились, а нежелательные взаимно уничтожились.
79
Рис. 6.3. Сравнение качеств управления САУ с И-регулятором и П-регулятором.
П-регулятор: (-) наличие статической ошибки; (+) высокое быстродействие;
И-регулятор: (+) отсутствие статической ошибки; (-) низкое быстродействие.
Рис. 6.4. Параллельная работа П- и И-регуляторов
Таким образом, мы «изобрели» один из самых совершенных законов
управления, имеющий наивысший рейтинг применения на практике –
пропорционально-интегральный закон управления, реализуемый в ПИрегуляторе.
3. Структурная схема ПИ-регулятора, его кривая разгона, закон
управления и передаточная функция
В структуру ПИ-регулятора входят следующие элементы (рис. 6.5):
80
1. Безынерционное звено для ввода составляющей в закон управления, пропорциональной рассогласованию (t) = g(t) – y(t) между
задающим воздействием g(t) и выходом объекта y(t).
2. Идеальное интегрирующее звено для ввода составляющей в закон
управления, пропорциональной интегралу от рассогласования.
3. Узел (развилка), размножающий сигнал рассогласования на два
канала (канал П-составляющей и канал И-составляющей).
4. Сумматор, осуществляющий формирование управляющего воздействия (как сумму выходов каналов П- и И-составляющих).
ПИ-регулятор
(t) = g(t) – y(t)
Рассогласование
П-составляющая
И-составляющая
u(t)
Управляющее
воздействие
Рис. 6.5. Структура ПИ-регулятора
Глядя на рис. 6.5, можно догадаться, что кривая разгона ПИрегулятора (рис. 6.6) может быть построена как сумма двух кривых разгона: для П-составляющей (рис. 5.4) и для И-составляющей (рис. 6.2а).
Рис. 6.6. Кривая разгона ПИ-регулятора (реакция на входное воздействие – ступенчатое рассогласование (t) = g(t) – y(t) между задающим воздействием g(t) и выходом объекта y(t))
81
Закон управления, реализуемый ПИ-регулятором, получается как
частный случай из общей формы линейных законов управления (5.1) (все
составляющие, кроме первых двух, отсутствуют):
t
u(t )  k p ·  (t )  k i ·   ( )d ,
(6.8)
0
где kp, ki – настроечные параметры ПИ-регулятора, отражающие вклады
П- и И-составляющих в управляющее воздействие, подаваемое на объект.
Параметры kp, ki являются размерными величинами:
[размерность входа объекта]
kp 
,
(6.9)
[размерность выхода объекта]
 
[размерность входа объекта]
.
[размерность выхода объекта]  [размерность времени ]
Обычно используют дифференциальную форму ПИ-закона (получается из (6.8) дифференцированием):
du
d
(6.10)
 k p ·  ki · (t ) .
dt
dt
Передаточная функция ПИ-регулятора – это отношение изображения
U(p) его выхода – управляющего воздействия u(t) – к изображению  (p)
его входа – рассогласования (t). Применяя преобразование Лапласа к
(6.9), получим:
p·U ( p)  ( p·k p  ki )·( p) .
ki  
Отсюда найдем передаточную функцию:
k
U ( p)
(6.11)
WПИ ( p) 
 kp  i .
E ( p)
p
Можно было бы получить формулу для передаточной функции, используя теорему 2 алгебры структурных преобразований (о передаточной
функции звеньев, соединенных параллельно): WПИ(p) есть сумма передаточных функций безынерционного звена (П-составляющая) и идеального интегрирующего звена (И-составляющая).
4. Исследование свойств САУ с ПИ-регулятором
Направления исследования – те же, как и выбранные нами при изучении П-закона:
1. Анализ качества отработки задающих воздействий и подавления возмущений. Мы ожидаем, что эти процессы будут проходить почти так же быстро, как и в системе с П-регулятором, и
при этом исчезнет статическая ошибка, как и в системе с Ирегулятором.
82
2. Анализ чувствительности САУ с ПИ-регулятором. Мы ожидаем, что в системе будут подавляться дрейф и колебания параметров объекта (благодаря наличию обратной связи).
3. Анализ использования ПИ-закона в системе программного
управления. Мы ожидаем, что качество управления будет сильно зависеть от динамичности изменений задания: при быстрых
изменениях задающих воздействий управляющий сигнал, скорее
всего, не будет успевать их отработать.
4. Анализ возможностей использования ПИ-закона в следящей системе (т. е. в такой, задающее воздействие в которой является
недетерминированным, до начала управления неизвестным и
значения которого формируются в реальном времени в темпе с
работой САУ). Мы ожидаем, что качество управления будет
сильно зависеть от степени предсказуемости задающего воздействия: если будущие значения заданий окажутся сильно коррелированными с текущим значением, то качество управления,
скорее всего, окажется приемлемым. При мало предсказуемых
изменениях задания система с ПИ-регулятором, скорее всего, не
будет успевать отследить эти изменения.
Замечание. Процесс моделирования полезно предварить формированием гипотез об
ожидаемых результатах. Прием «предчувствия» результата исследования, проводимого
методами моделирования, для инженера очень продуктивен, поскольку формирует в нем
критическое отношение к результатам моделирования, позволяющее ответить на вопрос:
является ли результат моделирования артефактом или же он отражает реальные свойства
системы.
4.1. Качество отработки ступенчатых заданий и постоянных
возмущений в САУ с ПИ-регулятором
Качество отработки ступенчатых заданий и постоянных (во времени)
возмущений в САУ с ПИ-регулятором иллюстрируется рис. 6.7. На нем
представлены результаты отработки ступенчатого задания и подавления
постоянного возмущающего воздействия в сравнении с качеством управления в САУ с П-регулятором, в структуру которого введено корректирующее звено. Мы видим, что наши ожидания оправдались: при практически одинаковом характере динамических процессов в САУ с ПИрегулятором постоянное возмущение подавляется до нулевой статической ошибки (в САУ с П-регулятором, как мы знаем, статическая ошибка
подавления возмущений неустранима).
На рис. 6.8 при тех же данных о задающем воздействии и о возмущении, что и для рис. 6.7, приведены результаты сравнения качества
управления в системах с ПИ- и И-регуляторами. Мы видим, что если отключить П-составляющую, но оставить то же значение И-составляющей,
которое было использовано в САУ с ПИ-регулятором, качество управле83
ния станет неудовлетворительным (рис. 6.8а: эффект сильной колебательности и недопустимого перерегулирования). Причина – ухудшение
запаса устойчивости. Если же снизить настроечный параметр ki Ирегулятора так, чтобы в САУ с этим регулятором получалось такое же
перерегулирование, как и в САУ с ПИ-регулятором, то качество управления в САУ с И-регулятором тоже будет плохим – на этот раз из-за потери
быстродействия (рис. 6.8б, пунктир).
а)
б)
1 – участки отработки задающего воздействия (возмущений нет); 2 – участки подавления
возмущающего воздействия.
Рис. 6.7. Качество отработки задающего воздействия и подавления возмущений в САУ с
ПИ-регулятором (рис. а). Иллюстрируется отсутствие статической ошибки. Для сравнения
(рис. б) показано качество отработки задания (с коррекцией) и подавления возмущения в
САУ с П-регулятором. Иллюстрируется полезный эффект ПИ-регулятора: при том же
качестве динамики в САУ с ПИ-регулятором подавляется постоянное возмущающее
воздействие
Таким образом, ПИ-регулятор выигрывает как по сравнению с
П-регулятором (устраняет статическую ошибку при подавлении постоянных возмущений), так и по сравнению с И-регулятором (при одном и том же значении перерегулирования существенно повышает
быстродействие отработки задающих воздействий и подавления возмущений). Платой за эти полезные эффекты является некоторое
усложнение процесса настройки параметров регулятора (приходится
настраивать два параметра, а в регуляторах-конкурентах – только
один).
84
а) иллюстрируется необходимость снижения настроечного параметра И-регулятора
для достижения такого же перерегулирования, как и в САУ с ПИ-регулятором (быстродействие САУ с ПИ-регулятором существенно выше)
б) динамика САУ с И-регулятором при том
же настроечном параметре, что и при Исоставляющей в ПИ-регуляторе (качество
динамики неудовлетворительное)
Рис. 6.8. Сравнение качества отработки задающего воздействия и подавления ступенчатого
возмущения в САУ с ПИ-регулятором и в САУ с И-регулятором
4.2. Анализ чувствительности САУ с ПИ-регулятором к изменению коэффициента усиления объекта
Результаты анализа чувствительности САУ с ПИ-регулятором к изменению коэффициента усиления объекта представлены на рис. 6.9
(скачкообразное изменение коэффициента) и 6.10 (скачкообразное изменение, затем линейный дрейф). На рис. 6.11 – 6.13 чувствительность ПИрегулятора сравнивается с чувствительностью конкурентов (П- и Ирегуляторов). Настроечные параметры регулятора в ходе вычислительного эксперимента не изменялись.
Мы видим (рис. 6.9, 6.10), что за счет интегральной составляющей
ПИ-регулятор подавляет довольно существенное параметрическое возмущение (скачкообразное уменьшение коэффициента усиления на 50 %
(рис. 6.9а и 6.10а) и скачкообразное увеличение коэффициента усиления
на 30 % (рис. 6.9б и 6.10б)).
85
а)
б)
1 – участки отработки задающего воздействия при постоянном коэффициенте усиления
объекта; 2 – участок отработки ступенчатого параметрического возмущения (скачкообразное уменьшение коэффициента усиления объекта); 3 – участок отработки ступенчатого параметрического возмущения (скачкообразное увеличение коэффициента усиления объекта).
Рис. 6.9. Качество управления в САУ с ПИ-регулятором: отработка ступенчатого задающего
воздействия и подавление ступенчатого параметрического возмущающего воздействия
а)
б)
1 – участки отработки задающего воздействия при постоянном коэффициенте усиления
объекта; 2 – участок отработки ступенчатого параметрического возмущения (скачкообразное уменьшение коэффициента усиления объекта и линейный дрейф на уменьшение); 3 –
участок отработки ступенчатого параметрического возмущения (скачкообразное увеличение коэффициента усиления объекта и линейный дрейф на увеличение).
Рис. 6.10. Качество управления в САУ с ПИ-регулятором: отработка ступенчатого
задающего воздействия и подавление ступенчатого параметрического возмущающего
воздействия с последующим линейным дрейфом
Разберем, имеется ли ограничение на диапазон параметрических
возмущений. Мы уже знаем, что увеличение настроечного параметра П86
регулятора kp приводит к улучшению точности воспроизведения задания
в статике, но может резко ухудшить динамику вплоть до неустойчивости
(см. рис. 5.5б). Но тот же эффект может получиться, если настроечный
параметр kp останется прежним, а увеличится коэффициент усиления
объекта (в формулу для передаточной функции САУ (5.4) эти коэффициенты входят в виде произведения, т. е. в форме общего коэффициента
усиления САУ kобщ = ko∙kp). Поэтому изменение ko в сторону увеличения
тоже может существенно ухудшить динамику вплоть до неустойчивости,
а изменение в сторону уменьшения – снизить быстродействие системы.
Поэтому параметрические возмущения, неизбежно возникающие при
эксплуатации САУ, гораздо опаснее внешних: последние не могут вызвать явлений неустойчивости.
На рис. 6.11, 6.12 приведены результаты сравнения чувствительности ПИ- и П-регуляторов. Мы видим (рис. 6.11б), что при использовании
П-регулятора с настроечным параметром kp, таким же, как коэффициент
при П-составляющей в ПИ-регуляторе, в САУ с П-регулятором линейный дрейф коэффициента усиления объекта не подавляется: рассогласование между задающим воздействием и выходом САУ увеличивается с
течением времени. Это объясняется тем, что параметр корректирующего
звена, введенный в САУ с П-регулятором, теряет свои корректирующие
свойства (из-за отклонения коэффициента усиления объекта ko от расчетного значения, принятого для определения параметров корректирующего
звена). Попытка уменьшить влияние дрейфа коэффициента усиления
объекта приводит к резкому ухудшению динамики (рис. 6.12). В то же
время в САУ с ПИ-регулятором имеет место эффект хорошего подавления дрейфа коэффициента усиления объекта за счет интегральной добавки (рис. 6.11а): в САУ имеется лишь небольшая постоянная во времени
статическая ошибка.
87
а)
б)
Рис. 6.11. Сравнение чувствительности САУ с ПИ-регулятором (рис. а) и САУ с
П-регулятором (рис. б). Настройки П-составляющей в обеих САУ одинаковы
Рис. 6.12. Снижение чувствительности САУ с П-регулятором к изменению коэффициента
усиления объекта за счет увеличения значения настроечного параметра kp. Резкое
ухудшение динамики
На рис. 6.13 представлены результаты сравнения чувствительности
ПИ- и И-регуляторов. Мы видим, что если использовать настроечный параметр И-регулятора ki, такой же, как коэффициент при И-составляющей
ПИ-регулятора (рис. 6.13б), то качество динамики САУ получится неудовлетворительным (сильная колебательность и недопустимое перерегулирование). Если же снизить ki И-регулятора так, чтобы уменьшить перерегулирование до приемлемого значения, то величина статической ошибки
88
получится больше, а быстродействие – существенно ниже, чем в САУ с
ПИ-регулятором.
1 – участки отработки задающего воздействия при постоянном коэффициенте усиления
объекта; 2 – участки отработки ступенчатого параметрического возмущения (скачкообразное уменьшение коэффициента усиления объекта и линейный дрейф на уменьшение).
а) в САУ с И-регулятором постоянная статическая ошибка больше, а быстродействие
ниже, чем в САУ с ПИ-регулятором; для
САУ с И-регулятором ki выбран из условия
достижения статического режима за то же
время, что и в САУ с ПИ-регулятором
б) в САУ с И-регулятором параметр
настройки ki тот же, что и при Исоставляющей в САУ с ПИ-регулятором;
качество динамики неудовлетворительное
из-за сильной колебательности и недопустимого перерегулирования
Рис. 6.13. Сравнение качества отработки параметрического возмущения (ступенька и
линейный дрейф) в САУ с ПИ- и И-регуляторами
Таким образом, ПИ-регулятор в чувствительности к параметрическим возмущениям также выигрывает как по сравнению с Прегулятором (не допускает роста рассогласования между заданием и
выходом при линейном дрейфе коэффициента усиления объекта), так
и по сравнению с И-регулятором (при одном и том же значении перерегулирования существенно повышает быстродействие отработки задающих воздействий и снижает статическую ошибку из-за дрейфа коэффициента усиления объекта).
89
4.3. Использование ПИ-закона в системе программного управления
Результаты анализа использования ПИ-закона в системе программного управления представлены на рис. 6.14. Напомним, что в системе
программного управления (в отличие от систем автоматической стабилизации) главным режимом является не статика, а динамика: задающие
воздействия изменяются настолько часто, что статический режим САУ
может не достигаться. Задающее воздействие в системах программного
управления заранее, до начала управления, известно (т. е. задан его график на весь период управления). Пример системы программного управления – САУ закалкой стальных изделий. Естественно, графики задающих
воздействий очень разнообразны и не типизируются. Для испытаний пригодности закона управления используются типовые тестовые сигналы
(например, синусоидальные). Мы выберем задающее воздействие в форме,
сложной для воспроизведения: меандровый сигнал (т. е. последовательность периодических изменений с прямоугольными участками, рис. 6.14).
Мы видим (рис. 6.14), что (как мы и предполагали) точность этого
воспроизведения сильно зависит от периодичности смены значения меандра: от очень хорошего (2000 с) до совершенно неудовлетворительного
(100 с). По мере увеличения частоты меандра растет отставание выхода
объекта по фазе – вплоть до почти противофазности при периодичности
смены значений меандра 100 с.
Замечание. Это явление объясняется инерционностью объекта управления. Для преодоления инерционности нужно было бы повысить коэффициент kp при пропорциональной
части ПИ-закона, но предел этому увеличению ставит появление сильного перерегулирования и даже неустойчивости.
Таким образом, ПИ-закон управления не всегда может быть
успешно использован в системах программного управления: при
несоответствии частотных свойств задающего воздействия частотным
свойствам объекта управления не удается найти значения настроечных
параметров ПИ-регулятора, при которых точность воспроизведения
изменяющегося задающего воздействия была бы удовлетворительной
(повышение коэффициента при пропорциональной части с целью преодоления инерционности объекта приводит к недопустимому перерегулированию или даже к неустойчивости).
90
Рис. 6.14. Качество САУ с ПИ-регулятором. Отработка меандрового задающего воздействия
4.4. Использование ПИ-закона в следящей системе
Проанализируем перспективы использования ПИ-закона в следящей
системе. Напомним, что в следящих системах (в отличие от систем программного управления) задающее воздействие заранее неизвестно; оно
формируется в реальном времени, в ходе работы объекта (пример объекта, для которого используется следящая система – манипуляторы). Мы
ожидаем, что качество работы САУ с ПИ-регулятором будет зависеть от
того, насколько «гладким», медленно изменяющимся во времени (а, следовательно, предсказуемым) является задающее воздействие.
Во многих следящих системах задающее воздействие, являясь неизвестным, не относится к числу случайных процессов, подчиняющихся
91
законам теории вероятностей. Но для тестирования ПИ-закона мы выберем задающие воздействия именно в форме случайного процесса, т. к.
для него имеется возможность количественно измерить степень предсказуемости будущих значений и, благодаря этому, проследить, как она влияет на качество САУ.
Напомним, что наиболее употребительным «измерителем» степени
связи будущих значений задающего воздействия z(t) (случайного процесса) с текущим значением является период спада нормированной корреляционной функции Kz( ) до значения 0.3…0.4. Напомним понятие
«период спада».
Из курсов «Теория вероятностей», «Математическая статистика» и «Теория случайных функций» известно, что нормированная корреляционная функция (т. е. такая, значения которой принадлежат интервалу
[ –1;1]) определяется формулой:
(6.12)
На рис. 6.15 показаны графики одного и того же случайного процесса с двумя различными сдвигами времени  между ними. Мы видим,
что если «будущее» опережает «настоящее» не намного (рис. 6.15б), то
по текущим значениям можно почти точно это «будущее» предсказать
(рис. 6.15а и рис. 6.15б очень сходны). Отдаленное будущее (рис. 6.15в)
уже ничем не напоминает текущие значения, и предсказать можно только
среднее значение (математическое ожидание) случайного процесса.
Примечание: эти рассуждения справедливы только для стационарного случайного
процесса, т. е. такого, в котором его статистические характеристики (в частности, математическое ожидание, дисперсия и др.) постоянны.
Если вычесть из z(t) его среднее значение, получим так называемый
центрированный случайный процесс ~z (t ) : его среднее значение равно 0
(именно такие процессы показаны на рис. 6.15). Зададимся , вычислим
z (t )·~z (t   ) , а затем усредним эти произвеt  0,..., tmax произведения ~
дения. Если ~z (t   ) почти совпадает с ~
z (t ), то знаки этих значений почти всегда будут одними и теми же, поэтому почти все произведения
~
z (t )·~z (t   ) будут положительными, соответственно среднее значение
этого произведения будет положительным (и тем большим, чем более
похожи ~z (t   ) и ~
z (t )).
Если же ~z (t   ) и ~z (t ) не сходны (как рис. 6.15а и 6.15в), то знаки
значений ~z (t   ) и ~z (t ) будут то совпадать, то различаться. Поэтому
92
произведения ~
z (t )·~
z (t   ) будут иметь для разных t разные («пестрые»)
знаки, соответственно среднее значение произведения будет малым (и
тем ближе к нулю, чем менее сходны ~z (t   ) и ~
z (t )).
Рис. 6.15. Иллюстрация к измерению связи текущих и будущих значений случайного
процесса
Таким образом, корреляционная функция (числитель которой как
раз и есть среднее значение произведения ~
z (t )·~z (t   ) , см. (6.12)) может
показать, насколько сильна связь между текущим значением случайного процесса z(t) с его будущим значением z(t +  ). Для того чтобы сравнивать различные случайные процессы между собой, корреляционные функции приводят к интервалу [–1;1] путем деления на дисперсию (как в (6.12)). Практически можно считать, что значения z(t +  ) и
z(t) не связаны между собой, если значение корреляционной функции
Kz( ) меньше 0.4.
Определение: величина интервала [0;  *] называется периодом спада корреляционной функции, если    * | Kz( ) | < 0.4.
Проведем испытания следящих систем с ПИ-регулятором, задающие
воздействия в которых имеют различные периоды спада корреляционной
функции (и, соответственно, различные возможности предсказать будущие значения по текущим). Результаты показаны на рис. 6.16.
93
Корреляционная функция Kz()
Выход объекта
Задающее воздействие
Область значимой корреляции
Задающее воздействие
Корреляционная функция Kz()
94
Выход объекта
Область значимой
корреляции
Корреляционная функция Kz()
Задающее воздействие
Выход объекта
Область значимой
корреляции
Рис. 6.16. ПИ-регулятор в следящей системе. Различная корреляция между текущим и будущим
(отстоящим на  тактов от текущего) значениями задающего воздействия
Мы видим (рис. 6.16), что (как мы и предполагали) точность воспроизведения стохастического задающего воздействия зависит от его
степени коррелированности. По мере уменьшения времени спада корреляционной функции задающего воздействия точность снижается, качество управления ухудшается (вплоть до неудовлетворительного).
Таким образом, ПИ-закон управления не всегда может быть
успешно использован в следящих системах: если время спада корреляционной функции задающего воздействия существенно меньше
показателя, характеризующего инерционность объекта управления
(например, суммы постоянных времени – удобный измеритель инерционности для объектов с апериодическими переходными функциями), то качество воспроизведения задающего воздействия будет неудовлетворительным.
Замечание (к понятию «неудовлетворительное качество управления»). Измерения качества основаны на вычислении нормированной взаимной корреляционной функции между
задающим воздействием и выходом объекта. Эта функция достигает максимального значения при некотором сдвиге во времени между значениями задающего воздействия и выхода
объекта (сдвиг объясняется тем, что выход объекта отстает по фазе от задающего воздействия из-за инерционности объекта и интегрирующих свойств регулятора). Если максимальное значение взаимной корреляционной функции не превышает 0.5, качество воспроизведения задающего воздействия системой управления считается неудовлетворительным:
его отслеживание будет происходить с недопустимо большими погрешностями.
5. Сводка свойств системы управления с ПИ-регулятором
Исследования, описанные в п. 4, позволяют сделать следующие выводы: САУ с ПИ-регулятором свойственны следующие позитивные качества, благодаря которым ПИ-регулятор является самым распространенным общепромышленным регулятором:
 (t )  0 . Это свойство вы1. Отсутствие статической ошибки: lim
t 
годно отличает системы автоматической стабилизации с ПИрегуляторами от систем с П-регуляторами.
2. Хороший показатель быстродействия САУ с ПИ-регулятором.
Быстродействие близко к быстродействию САУ с П-регулятором
(этот показатель в САУ с П-регулятором всё же лучше). Быстродействие САУ с ПИ-регулятором гораздо выше быстродействия
САУ с И-регулятором.
3. Пониженная (по сравнению с П-регулятором и И-регулятором)
чувствительность САУ к неточностям сведений о коэффициенте
усиления объекта (по сравнению с разомкнутой системой).
4. Широкая область применения в системах с различными целями
управления – стабилизации, программного управления, слежения.
Выявлены также недостатки ПИ-закона управления:
1. Более сложная (по сравнению с П- и И-регуляторами) структура,
трудности настройки параметров ПИ-регулятора (из-за наличия
95
двух, а не одного, как в П- и И-регуляторах, настроечных параметров).
2. Возможность сильной колебательности и даже неустойчивости
переходных процессов в САУ.
3. Невысокая точность воспроизведения высокочастотных задающих
воздействий (в системах программного управления и слежения).
6. Нужны ли дальнейшие усложнения закона управления?
Почему не всегда удается добиться нужного качества управления за
счет увеличения параметра ki ПИ-регулятора? По существу мы уже ответили на первый из вопросов триады (зачем?) в разделах 4.3 и 4.4: в системах программного управления и в следящих системах качество управления может оказаться неудовлетворительным.
Следуя триаде «зачем?  почему?  как?», мы должны выяснить,
почему не всегда удается добиться нужного качества управления за счет
очевидного приема – увеличения параметров настройки ПИ-регулятора.
При исследовании переходных процессов в системе с ПИ-регулятором
мы обнаруживаем, что увеличение параметра ki, отражающего вклад Исоставляющей в ПИ-закон управления, может вызвать явление неустойчивости. Разберемся в его причине.
Явление неустойчивости, свойственное замкнутым системам управления, на первый взгляд кажется таинственным. В самом деле: по сравнению с объектом регулятор является «энергетическим ничтожеством»
(например, мощность котлотурбинного агрегата отличается от мощности,
потребляемой регулятором температурного режима в нем, в 40 млн. раз,
и не случайно в теории управления мощность регулятора не учитывается
совсем). Почему же это ничтожество может привести к тому, что график
температурного режима огромного агрегата может оказаться графиком
расходящихся колебаний – вплоть до поломки агрегата?
Замечание. Полезны примеры, в которых наблюдались неустойчивые режимы на реальном объекте. Один из таких примеров – последствия неудачной настройки регулятора
уровневого режима в большом ирригационном канале, разделенном перегораживающими
водорегулирующими сооружениями на отсеки. В результате неверно выбранных настроек в
канале возникли волновые процессы с увеличивающейся высотой волн. Причина неустойчивости: каждая следующая волна, порожденная управляющим воздействием (изменением
положения затвора водорегулирующего сооружения, подающего воду в отсек канала), оказывалась синфазной с волной, отраженной от нижележащего водорегулирующего сооружения. В результате происходило сложение амплитуд этих волн. Амплитуда новой отраженной волны оказывалась выше предыдущей, снова накладывалась на волну, порожденную
регулятором, и амплитуда колебаний уровня воды в канале увеличивалась от цикла к циклу.
Этот пример подводит к пониманию существа неустойчивости. Сигнал управления (включение двигателя, перемещающего затвор водорегулирующего сооружения) имеет пренебрежимо малую мощность. Но, поскольку управляющие воздействия подаются во времени
так неудачно, что вызывают наложение порожденной и отраженной волн, огромная мощность объекта (а совсем не ничтожная мощность регулятора) используется для его «раскачки». Данный пример показывает, насколько опасно включать систему управления без предварительного расчета ее параметров, гарантирующего отсутствие явлений неустойчивости.
96
В лекционном курсе излагаются математические основы исследования устойчивости (в частности, изучаются необходимые и достаточные
условия, гарантирующие устойчивость систем управления с непрерывным временем: отрицательность вещественных частей корней знаменателя передаточной функции системы). Но на практическом занятии полезно
обратиться не столько к абстракциям, сколько к физической сущности
явления неустойчивости.
Замечание. Прояснение физической сущности неустойчивости позволяет усилить мотивацию к изучению теоретических методов ее исследования; кроме того, удастся не только
добиться понимания того, зачем совершенствовать ПИ-закон управления, но и догадаться,
как это сделать, т. е. определить направление совершенствования ПИ-закона управления.
Из описания развития неустойчивых процессов в ирригационном
канале, приведенного выше, можно сделать вывод, что «порча» происходит из-за неправильного наложения последствий прошлых управляющих
воздействий на текущее управляющее воздействие. В ПИ-законе управления запоминание прошлых управлений производится за счет Идобавки, поэтому для простоты проанализируем причины неустойчивости в системе с И-регулятором. Напомним, что в САУ с И-регулятором
управляющее воздействие u(t) пропорционально интегралу от рассогласования (t) = z(t) – y(t) между задающим воздействием z(t) и выходом объекта y(t):
t
u (t )  ki ·  ( )d ,
(6.13)
0
где ki – настроечный параметр регулятора.
Мы видим, что по смыслу закона управления текущее значение
управляющего воздействия аккумулирует в себе все прошлые воздействия, которые влияли на величины рассогласований в период 0  θ < t.
Замечание. Напомним, что такой эффект запоминания прошлых действий пропорциональному регулятору не свойствен: величина управления определяется рассогласованием
только в текущий момент времени.
Рассмотрим самую простую задачу управления, целью которого является отработка ненулевых начальных условий при задающем воздействии,
равном нулю (т. е. приведение объекта в состояние покоя, при котором и
выход объекта, и все его производные равны нулю). Будем считать, что в
момент времени t = 0 выход объекта отличается от нуля, все производные
выхода равны нулю и управляющее воздействие равно нулю при t  0.
Варианты показаны на рис. 6.17 (намеренно в одинаковом масштабе,
для иллюстрации принципиальных изменений характера процессов в системе из-за неустойчивости):
1. Управляющее воздействие отсутствует (рис. 6.17а), что соответствует значению ki = 0 в формуле (6.13).
2. Управляющее воздействие рассчитывается по формуле (6.13) при
малом значении ki = ki(1) (рис. 6.17б). Явление неустойчивости не
97
возникает, изменения выхода объекта носят апериодический характер.
3. Управляющее воздействие рассчитывается по формуле (6.13) при
значении ki = ki(2) > ki(1) (рис. 6.17в), при котором явление неустойчивости также не возникает, но изменения выхода объекта
носят колебательный характер.
4. Управляющее воздействие рассчитывается по формуле (6.13) при
значении ki = ki(3) > ki(2) (рис. 6.17г), изменения выхода объекта также
носят колебательный характер, но амплитуды колебаний возрастают
от периода к периоду; имеет место явление неустойчивости.
Рис. 6.17. Характер изменений выхода объекта при различных значениях параметра
настройки И-регулятора
Замечание. Полезно привести пример, иллюстрирующий природу неустойчивости.
Рассмотрим процессы раскачки и торможения качелей. Для раскачки нужно в период движения качелей «вперед» вытягивать ноги вперед, а в период движения качелей «назад» подгибать ноги. Тогда малая энергия наших мускулов будет направлена согласно, синфазно с
направлением собственных колебаний качелей. А для торможения нужно действовать
наоборот: при движении качелей «вперед» подгибать ноги, а при движении «назад» – вытягивать их. Та же самая малая энергия мускулов будет направлена противофазно направлению собственных колебаний качелей, что приведет к затуханию колебаний. Этот пример
иллюстрирует важную роль разности фаз между выходом объекта (текущим положением
точки на качели) и управляющим воздействием (мускульным усилием): в зависимости от
значения этой разности система управления будет вести себя либо как система с положительной обратной связью (при этом амплитуда колебаний будет увеличиваться от периода к
периоду), либо как система с отрицательной обратной связью (при этом амплитуда колебаний будет уменьшаться от периода к периоду).
Выясним, какова разность фаз между выходом объекта и управляющим воздействием в системе с И-регулятором, в которой объект управления описывается дифференциальным уравнением не ниже 2-го порядка
(почему не ниже – поясним чуть позднее).
1. Выход И-регулятора отстает от его входа на 0.25 периода (это
легко проиллюстрировать интегралом от периодической функции
sin(ω∙t) с частотой ω: после интегрирования получим [–cos(ω∙t)], т. е.
98
периодическую функцию той же частоты, отстающую от sin(ω∙t)
на 0.25 периода).
2. Если объект представляет собой инерционное звено, то его выход
также отстает от входа, но это отставание зависит от частоты
входного сигнала: чем больше эта частота, тем больше отставание. Природа этого отставания – наличие инерции объекта. Из
лекционного курса мы знаем, что зависимость разности фаз между синусоидальным сигналом на выходе объекта, порожденным
синусоидальным сигналом на его входе, называется фазочастотной характеристикой объекта. На рис. 6.18 приведены фазочастотные характеристики двух апериодических звеньев – первого
и второго порядка. Мы видим, что при увеличении частоты разности фаз между выходом и входом этих объектов приближаются
соответственно к 0.25 периода и к 0.5 периода (т. е. по 0.25 периода на каждый порядок уравнения, описывающего динамику объекта с апериодической переходной характеристикой).
3. Общее фазовое отставание выхода объекта от управляющего воздействия равно сумме отставаний, вызванных И-регулятором и
самим объектом. Если И-регулятор используется для управления
объектом 1-го порядка, то общее отставание не превысит 0.5 периода. Если же И-регулятор используется для управления объектом 2-го (или более чем 2-го) порядка, то общее отставание может оказаться больше 0.5 периода.
Сдвиг фазы выходного сигнала по
отношению к входному сигналу
(фазочастотная характеристика φ (ω)),
апериодическое звено 1-го порядка
Сдвиг фазы выходного сигнала по
отношению к входному сигналу
(фазочастотная характеристика φ(ω)),
апериодическое звено 2-го порядка
Рис. 6.18. Фазочастотные характеристики апериодических объектов 1-го и 2-го порядка
Посмотрим, как соотносятся графики выхода объекта и управляющего воздействия, приведенного к выходу (т. е. с учетом отставания
выхода от управления по фазе) – иными словами, не того управления, ко99
торое мы подаем на вход, а управления, фактически действующего на
выход объекта.
На рис. 6.19 представлены графики выхода объекта и управления,
приведенного к выходу, для случая, когда, согласно частоте колебаний
выхода, отставание фазы выхода объекта по отношению к его входу
меньше 0.25 периода. Общее отставание графика выхода от графика
управляющего воздействия при этом меньше 0.5 периода. Мы видим, что
в системе с И-регулятором периодически возникают режимы, в которых
знаки выхода объекта и управляющего воздействия, приведенного к выходу, совпадают. В этих режимах регулятор действует так, как если бы
система управления была не с отрицательной, а с положительной обратной связью – т. е. регулятор подталкивает объект к новым колебаниям
вместо того, чтобы успокаивать колебания. Но продолжительность таких
режимов меньше, чем продолжительность «нормальных» режимов, в которых знаки выхода и управляющего воздействия, приведенного к выходу, противоположны. Образно можно сказать, что позитивные эффекты
отрицательной обратной связи сильнее негативных эффектов положительной связи. Система управления остается устойчивой.
Знаки выхода объекта и управляющего
воздействия СОВПАДАЮТ
Знаки выхода объекта и управляющего
воздействия ПРОТИВОПОЛОЖНЫ
Рис. 6.19. Управляющее воздействие отстает по фазе от выхода объекта меньше, чем на
половину периода. Система управления устойчива
Будем увеличивать настроечный параметр регулятора ki. Частота колебаний выхода объекта при этом будет возрастать (рис. 6.17), т. к. регулятор будет стремиться изменить выход быстрее. Но тогда при некоторой
частоте может оказаться, что отставание фазы выхода объекта по отношению к его входу превысит 0.25 периода (см. рис. 6.18).
100
Такая ситуация показана на рис. 6.20. Общее отставание графика
выхода от графика управляющего воздействия превышает 0.5 периода.
Мы видим, что и в этом случае в системе с И-регулятором периодически
возникают режимы, в которых знаки выхода объекта и управляющего
воздействия, приведенного к выходу, совпадают, т. е. система управления ведет себя так, как будто в ней используется положительная обратная
связь. Но, в отличие от рис. 6.19, продолжительность таких режимов
больше, чем продолжительность «нормальных» режимов, в которых знаки выхода и управляющего воздействия, приведенного к выходу, противоположны. Образно можно сказать, что позитивные эффекты отрицательной обратной связи слабее негативных эффектов положительной
связи. Система управления становится неустойчивой.
Знаки выхода объекта и управляющего
воздействия ПРОТИВОПОЛОЖНЫ
Знаки выхода объекта и управляющего
воздействия СОВПАДАЮТ
Рис. 6.20. Управляющее воздействие отстает по фазе от выхода объекта больше, чем на
половину периода. Система управления неустойчива
Между двумя областями значений настроечного параметра Ирегулятора, первая из которых соответствует устойчивой системе, а вторая – неустойчивой, существует значение ki, при котором продолжительность режимов совпадений знаков выхода и управления, приведенного к
выходу, равна продолжительности несовпадения этих знаков. В этом
случае в системе возникают незатухающие колебания (т. е. система находится на границе устойчивости, рис. 6.21).
Теперь становится понятно, почему неустойчивый режим в системе
с И-регулятором не возникает (естественно, если ki > 0, т. е. если САУ задумана как система с отрицательной обратной связью), когда объект является апериодическим звеном 1-го порядка. Фазочастотная характеристика такого объекта такова (рис. 6.12), что отставание выхода объекта от
входа по фазе никогда не превышает 0.25 периода. При этом общее от101
ставание графика выхода от графика управляющего воздействия никогда
не превысит 0.5 периода, продолжительность режимов совпадения знаков
выхода и управления, приведенного к выходу, всегда окажется меньше,
чем продолжительность «нормальных» режимов, в которых знаки выхода
и управляющего воздействия, приведенного к выходу, противоположны.
Процесс останется устойчивым (как на рис. 6.19) при любом положительном значении настроечного параметра И-регулятора ki.
Знаки выхода объекта и управляющего
воздействия ПРОТИВОПОЛОЖНЫ
Знаки выхода объекта и управляющего
воздействия СОВПАДАЮТ
Рис. 6.21. Управляющее воздействие отстает по фазе от выхода объекта ровно на половину
периода. Система управления находится на границе устойчивости
Замечание. Обратим внимание на трудности определения разности фаз между выходом и управляющим воздействием. Эти трудности связаны с необходимостью определения
частот колебаний выхода при каждом заданном значении настроечного параметра регулятора. Можно, конечно, представить себе, что эти частоты мы определим экспериментально.
Но объем такого эксперимента был бы огромен, вызвал бы длительные отклонения технологических показателей от нормы и поэтому оказался бы неприемлемым. Поэтому важны
теоретические методы исследования устойчивости, в которых привлекаются собственные
числа, характеристические уравнения, передаточные функции и их знаменатели, критерии
устойчивости.
Ответ на второй вопрос триады: «Почему не всегда удается добиться
нужного качества управления в САУ с ПИ-регулятором?» – получен:
прием улучшения качества, состоящий в увеличении значений настроечных параметров регулятора, может привести к неустойчивости.
7. Как усовершенствовать ПИ-закон управления?
Ответ на последний из вопросов триады «зачем?  почему?  как?»
очевиден: нужно блокировать сдвиг фазы, вызываемый И-составляющей
102
ПИ-закона управления. Можно предложить различные способы этой
блокировки, но логика «бритвы Оккама» предписывает выбрать простейший вариант. Если интегрирование вызывает отставание фазы, то
можно сразу догадаться, что опережение фазы (и тоже на четверть периода) произойдет, если в закон управления ввести дифференцирующую
добавку.
Получим пропорционально-интегрально-дифференциальный (ПИД)
линейный закон управления, воспринимаемый инженерами как некоторое логически законченное совершенство.
8. Контрольные вопросы
Можно ли устранить статическую ошибку регулятором, в качестве которого используется элементарное звено из группы звеньев с самовыравниванием?
2. Каковы преимущества И-закона управления?
3. Каковы недостатки И-закона управления?
4. В чем ПИ-регулятор выигрывает по сравнению с П-регулятором?
5. В чем ПИ-регулятор выигрывает по сравнению с И-регулятором?
6. Почему ПИ-закон управления не всегда может быть успешно использован в системах программного управления?
7. Почему ПИ-закон управления не всегда может быть успешно использован в следящих системах?
8. Каковы преимущества ПИ-закона управления?
9. Каковы недостатки ПИ-закона управления?
10. Как усовершенствовать ПИ-закон управления?
1.
103
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 7
ТЕМА: «ЛИНЕЙНЫЕ ЗАКОНЫ УПРАВЛЕНИЯ.
ПРОПОРЦИОНАЛЬНО-ИНТЕГРАЛЬНО-ДИФФЕРЕНЦИАЛЬНЫЙ
РЕГУЛЯТОР»
Время проведения практического занятия (аудиторные часы) – 2 часа, занятие должно проводиться с компьютерным сопровождением в связи с обширностью материала.
Время самостоятельной работы студента (дополнительные часы) – 2 часа.
Цель занятия: изучить типовой линейный закон управления – пропорционально-интегрально-дифференциальный (ПИД), получить представление о базовых свойствах САУ с регулятором этого вида.
Рассматриваемые вопросы:
1. Типовой ПИД-закон управления и его свойства.
2. Сводка изученных линейных законов управления.
1. Структурная схема ПИД-регулятора, его кривая разгона, закон
управления и передаточная функция
В структуру ПИД-регулятора входят следующие элементы (рис. 7.1):
1. Безынерционное звено для ввода составляющей в закон управления, пропорциональной рассогласованию (t) = g(t) – y(t) между
задающим воздействием g(t) и выходом объекта y(t).
2. Идеальное интегрирующее звено для ввода составляющей в закон управления, пропорциональной интегралу от рассогласования.
3. Узел (развилка), размножающий сигнал рассогласования на два
канала (канал П-составляющей и канал И-составляющей).
4. Сумматор, осуществляющий формирование управляющего воздействия (как сумму выходов каналов П- и И-составляющих).
ПИД-регулятор
П-составляющая
(t) = g(t) – y(t)
И-составляющая
Рассогласование
u(t)
Д-составляющая
Рис. 7.1. Структура ПИД-регулятора
104
Управляющее
воздействие
Кривая разгона ПИД-регулятора =
= (П-составляющая) +
+ (И-составляющая) +
+ (Д-составляющая)
Д-составляющая ПИД-закона
И-составляющая ПИД-закона
П-составляющая ПИД-закона
Глядя на рис. 7.1, можно догадаться, что кривая разгона ПИДрегулятора (рис. 7.2) может быть построена как сумма трех кривых разгона: для П-составляющей (рис. 5.4), И-составляющей (рис. 6.2а) и Дсоставляющей (которая, возможно, нуждается в пояснениях).
Рис. 7.2. Кривая разгона ПИД-регулятора как сумма кривых разгона П-, И- и Д-регуляторов
Пояснения к кривой разгона Д-регулятора. Как известно, кривая разгона является реакцией объекта на входной сигнал ступенчатой формы. Если бы можно было подать такой
сигнал на вход дифференцирующего звена, то оказалось бы, что при (– ) < t < 0 выход
дифференциатора был бы равен нулю (как производная от константы). Но и при
0 < t < (+ ) выход дифференциатора также был бы равен нулю по той же причине. При
t = (– 0), т. е. при подходе слева, выход дифференциатора устремляется в (+ ), поскольку
скорость нарастания входного ступенчатого сигнала бесконечно велика. При t = (+ 0) выход
дифференциатора возвращается из (+ ) к нулю. Естественно, на практике такое развитие
событий невозможно: в реальных процессах ступенчатые сигналы не встречаются. Всегда
присутствует некоторая инерционность, вследствие которой сигнал, трактуемый нами как
ступенчатый, на самом деле в окрестности t = 0 возрастает, хотя и очень быстро, но не
мгновенно. Соответственно производная этого сигнала (т. е. выход Д-регулятора) может
оказаться очень большой, но не бесконечно большой. Однако идеализация во многих задачах
допустима.
Таким образом, кривая разгона ПИД-регулятора имеет 4 характерных участка (рис. 7.2):
1. До появления входного ступенчатого сигнала выход ПИДрегулятора равен нулю.
2. В момент появления входного ступенчатого сигнала выход ПИДрегулятора устремляется в бесконечность.
3. Практически в тот же момент времени выход ПИД-регулятора
возвращается из бесконечности до значения, пропорционального
входному сигналу (Д-составляющая «отработала» и исчезла, Исоставляющая «не успела» начаться, П-составляющая определила
выход регулятора).
105
4. Затем начинается линейный рост выхода ПИД-регулятора под
действием И-составляющей, которая суммируется с постоянным
во времени вкладом П-составляющей.
Закон управления, реализуемый ПИД-регулятором, получается как
частный случай из общей формы линейных законов управления (5.1) (все
составляющие, содержащие кратные интегралы и производные выше 1-го
порядка, отсутствуют):
d ,
(7.1)
dt
0
где kp, ki, kd – настроечные параметры ПИД-регулятора, отражающие
вклады П-, И- и Д-составляющих в управляющее воздействие, подаваемое на объект. Параметры kp, ki, kd являются размерными величинами:
t
u (t )  k p ·  (t )  k i ·   ( )d  k d ·
[размерность входа объекта]
k   [размернос
,
ть выхода объекта]
p
ki  
[размерность входа объекта]
,
[размерность выхода объекта]  [размерность времени ]
k d   [размерность входа объекта]  [размерность времени ] .
[размерность выхода объекта]
Обычно используют дифференциальную форму ПИД-закона (получается из (7.1) дифференцированием):
du
d
d 2
(7.2)
 kp ·
 k i ·  (t )  k d · 2 .
dt
dt
dt
Передаточная функция ПИД-регулятора есть отношение изображения U(p) его выхода – управляющего воздействия u(t) – к изображению
 (p) его входа – рассогласования (t). Применяя преобразование Лапласа
к (7.2), получим:
p·U ( p)  ( p · k p  ki  p 2 · k d ) · ( p) .
Отсюда найдем передаточную функцию:
k
U ( p)
WПИД ( p) 
 k p  i  kd · p .
(7.3)
( p )
p
Можно было бы получить формулу для передаточной функции, используя теорему 2 алгебры структурных преобразований (о передаточной
функции звеньев, соединенных параллельно): WПИД(p) есть сумма передаточных функций безынерционного звена (П-составляющая), идеального интегрирующего звена (И-составляющая) и идеального дифференцирующего звена (Д-составляющая).
106
2. Свойства САУ с ПИД-регулятором
Можно было бы провести исследования свойств по той же методике,
что и в п. 4 практического занятия № 6, но продуктивнее попытаться
предсказать эти свойства, основываясь на роли Д-добавки, расширяющей
диапазон устойчивости САУ по сравнению с ПИ-регулятором.
Преимущества ПИД-закона управления
1. В системах автоматической стабилизации главные преимущества
ПИД-регулятора перед ПИ-регулятором сводятся к возможности существенно увеличить коэффициенты при П- и И-составляющих (за счет
чего значительно увеличится быстродействие без увеличения перерегулирования и колебательности). Действие Д-составляющей будет заметным только в моменты резких изменений задающих воздействий и / или
возмущений (при постоянных или почти постоянных внешних воздействиях производная выхода будет близка к нулю).
Рассмотрим пример отработки ступенчатого изменения задающего
воздействия в САУ с двумя вариантами регуляторов – ПИ и ПИД. На рис.
7.3 показан график выхода объекта в САУ с ПИ-регулятором, настроечные параметры kp, ki которого выбраны так, чтобы обеспечить минимально возможное время переходного процесса. Стремление уменьшить
время переходного процесса за счет его форсирования (увеличения kp, ki)
приводит к росту колебательности и, в конечном итоге, к неустойчивости.
Рис. 7.3. Динамика выхода объекта в САУ с ПИ-регулятором. Настройка на максимум
быстродействия
На рис. 7.4 показан аналогичный график в САУ с ПИД-регулятором.
Мы видим, что за счет введения дифференцирующей добавки область
устойчивости САУ расширилась настолько, что оказалось возможным
увеличить коэффициент при П-составляющей в 12 раз, а при И-составляющей в 5 раз (по сравнению с настройками ПИ-регулятора). За счет этого
значительно уменьшилось время переходного процесса и снизилось значение перерегулирования. Чтобы подчеркнуть эффекты улучшения качества управления, на рис. 7.5 показаны оба графика.
107
Рис. 7.4. Динамика выхода объекта в САУ с ПИД-регулятором. Настройка на максимум
быстродействия
Рис. 7.5. Сравнение динамики выхода объекта в САУ с ПИ- и ПИД-регуляторами.
Настройка на максимум быстродействия
Если установить значения kp, ki для ПИ-регулятора такими же, какие
использованы в ПИД-регуляторе, то система управления станет неустойчивой, что иллюстрирует благоприятное стабилизирующее влияние Дсоставляющей. На рис. 7.6 – вынужденно иной масштаб, вследствие чего
ступенька изменения задающего воздействия почти незаметна. Момент
изменения показан.
Замечание. Если в практике работы реальной системы управления часто встречаются
режимы с почти ступенчатыми изменениями задания, ПИД-закон (7.1) целесообразно подправить, исключив из него производную задающего воздействия. Получим такой закон
управления:
t
u (t )  k p ·  (t )  ki ·   ( )d  k d ·
0
dy .
dt
Именно для такого закона рассчитаны примеры, показанные на рис. 7.4, 7.5.
108
(7.4)
Рис. 7.6. Потеря устойчивости САУ с ПИ-регулятором. Настройки – те же, что и в
ПИД-регуляторе
Если использовать закон управления (7.1), то в момент ступенчатого
изменения задающего воздействия на выходе объекта будет наблюдаться
резкий скачок, направление которого противоположно направлению ступеньки задания (рис. 7.7, обратите внимание на масштаб оси абсцисс),
качество управления будет неудовлетворительным. (Об этом авторы
учебников по основам теории управления обычно не упоминают, поскольку при расчете примеров они чаще всего используют постоянные, а
не ступенчатые входы).
2. Рассмотрим возможности ПИД-регулятора в системах программного управления. После сказанного в п. 1 становится ясно, что от ПИДрегулятора не следует ожидать заметного улучшения качества управления
(по сравнению с ПИ-регулятором), если задающие воздействия – плавные
функции времени (т. е. если показатели инерционности входных воздействий превышают показатели инерционности объекта). На рис. 7.8 показаны процессы отработки медленно изменяющегося задающего воздействия
в САУ с ПИ-регулятором (рис. 7.8а) и с ПИД-регулятором (рис. 7.8б). Мы
видим, что качество управления практически одинаковое. Следуя «бритве Оккама», посоветуем в этом случае отказаться от ПИД в пользу более
простого ПИ-регулятора.
109
Рис. 7.7. Негативное влияние производной ступенчатого изменения задающего воздействия
а) САУ с ПИ-регулятором, настройка на высокую точность воспроизведения задания
б) САУ с ПИД-регулятором, настройка на
высокую точность воспроизведения задания
Рис. 7.8. Сравнение качества воспроизведения медленно изменяющегося задающего
воздействия в САУ с ПИ-регулятором и в САУ с ПИД-регулятором
3. При высокочастотных изменениях задающих воздействий в системах программного управления ПИД-регулятор, в отличие от п. 2,
обеспечит более высокое качество управления (но в этом случае не за
счет возможности установить форсирующие параметры настройки при
П- и И- составляющих без потери устойчивости, а за счет «собственного»
форсирующего действия, возникающего при дифференцировании задания).
На рис. 7.9 показан процесс воспроизведения высокочастотного меандрового задающего воздействия в САУ с ПИ-регулятором. Мы видим,
что качество воспроизведения неудовлетворительное: выход объекта отстает от задания почти на половину периода.
110
На рис. 7.10 показан аналогичный процесс в САУ с ПИДрегулятором. За счет Д-добавки качество управления существенно улучшилось. Причина – в резком форсировании процесса в моменты изменения меандра за счет введения дифференцирования задающего воздействия (в этом случае использовался алгоритм (7.4)).
Рис. 7.9. Неудовлетворительное воспроизведение высокочастотного меандрового задания в
САУ с ПИ-регулятором
Рис. 7.10. Улучшение качества управления при воспроизведении высокочастотного
меандрового задания за счет введения Д-добавки
4. В следящих системах так же, как и в системах программного
управления, преимущества ПИД-регулятора проявятся только при отслеживании высокочастотных изменений заданий (т. е. в том случае, когда
111
период спада корреляционной функции задающего воздействия значительно меньше времени достижения нового статического режима в объекте).
На рис. 7.11 показан процесс отслеживания высокочастотного задающего воздействия в САУ с ПИ-регулятором. Мы видим, что выход объекта «не успевает» за изменениями задания, сглаживает их. Качество отслеживания низкое.
Рис. 7.11. Низкое качество отслеживания высокочастотного случайного задающего
воздействия в следящей системе с ПИ-регулятором
За счет форсированного введения производной задающего воздействия ПИД-регулятор обеспечивает гораздо более высокое качество отслеживания случайного задающего воздействия (рис. 7.12)
Рис. 7.12. Улучшение качества отслеживания высокочастотного случайного задающего
воздействия в следящей системе с ПИД-регулятором (по сравнению с ПИ-регулятором)
Мы рассмотрели источники преимущества ПИД-регулятора перед
ПИ-регулятором в системах автоматической стабилизации, программного управления и слежения. Теперь остановимся на недостатке. Он очевиден: имеются трудности в настройке регулятора. Найти вручную такие
значения сразу трех параметров (kp, ki, kd), чтобы обеспечить хорошее ка112
чество управления, – довольно трудная задача (особенно если неизвестна
хотя бы ориентировочно область приемлемых значений параметров).
3. Сводка свойств системы управления с ПИД-регулятором
Для систем с ПИД-регулятором характерны следующие позитивные
свойства, благодаря которым удается обеспечить приемлемое качество управления в ряде случаев, когда САУ с ПИ-регулятором неработоспособны:
1. В системах автоматической стабилизации ПИД-регулятор обеспечивает гораздо более высокое быстродействие и (одновременно) снижает значение перерегулирования (по сравнению с ПИрегулятором). Это качество проявляется при отработке ступенчатых изменений внешних воздействий.
2. В системах программного управления и слежения ПИДрегулятор предпочтительнее ПИ-регулятора только при высокочастотных (по сравнению с частотными свойствами объекта) изменениях задающих воздействий.
3. Д-добавка способствует расширению зоны устойчивости системы
управления (блокирует отставание фазы выхода системы по отношению к управляющему воздействию, вызываемое действием
И-составляющей закона управления).
4. Благодаря И-составляющей ПИД-регулятор сохраняет позитивные свойства ПИ-регулятора (отсутствие статической ошибки,
высокое быстродействие, пониженную чувствительность к неточностям сведений о коэффициенте усиления объекта). Дсоставляющая улучшает эти свойства.
Выявлены также недостатки ПИД-закона управления:
1. Более сложная (по сравнению с П-, И- и ПИ-регуляторами)
структура, трудности настройки параметров ПИД-регулятора (изза наличия трех настроечных параметров, а не одного, как в П- и
И-регуляторах, и не двух, как в ПИ-регуляторе).
2. Наличие перерегулирования при настройке параметров регулятора на максимум быстродействия.
3. Если частотный спектр задающих воздействий сильно смещен в сторону высоких частот (по сравнению с полосой пропускания объекта),
то ПИД-регулятор (как и все регуляторы, рассмотренные выше) не
может обеспечить хорошее качество воспроизведения заданий.
Общий вывод: поскольку ПИД-регулятор сложнее, чем рассмотренные
выше, то использование ПИД-закона управления целесообразно только тогда, когда нужное качество управления не может быть обеспечено регуляторами с более простыми законами (в частности, ПИ-регулятором).
113
4. Нужны ли дальнейшие усложнения закона управления?
Ответов на вопрос зачем? – три, они связаны со стремлением устранить недостатки ПИД-закона, перечисленные выше.
1. Нужны механизмы автоматической настройки параметров регулятора. Такая возможность обеспечивается системами управления, обладающими механизмами адаптации (напомним, что в
теории управления термин адаптация трактуется как свойство
системы управления отрабатывать не только внешние, но и внутренние возмущающие воздействия). В настоящее время алгоритмы адаптации встраиваются во все современные общепромышленные цифровые регуляторы.
2. Нужны более совершенные законы управления, в которых сочетается высокое быстродействие с низким (или вообще отсутствующим) перерегулированием. В рамках линейных законов
управления это в общем случае недостижимо, но можно попытаться найти решение при использовании нелинейных законов
(тема следующего практического занятия).
3. Нужны алгоритмы, обеспечивающие воспроизведение высокочастотных задающих воздействий в системах программного управления и слежения.
5. Сводка изученных линейных законов управления
Различные комбинации кратных интегралов и производных высоких
порядков, предусмотренные общей формой линейного закона управления
(5.1), в общепромышленных регуляторах не используются в связи с трудностями настройки параметров, опасностью неустойчивости и большими
погрешностями определения производных выхода объекта.
В типовой общепромышленный регулятор встраивается ПИД-закон
управления, из которого можно получить все остальные законы управления, в
которых не предусматривается интегрирование рассогласования выше однократного и дифференцирование рассогласования выше 1-го порядка. Обобщенная форма типового линейного непрерывного закона управления:
t
d
(7.5)
u (t )  k p ·  (t )  k i ·   ( )d  k d ·
.
dt
0
Из (7.5) в качестве частных случаев следуют все типовые линейные
законы, приведенные в табл. 1.
Мы видим, что все законы управления получаются из общей формулы
(7.5). Этот факт используют при серийном производстве регуляторов: все они
выпускаются как ПИД-регуляторы с возможностью получить из них все законы управления табл. 1 путем выключения ненужных настроечных параметров.
114
Таблица 1
Типовые линейные законы управления
Получение формулы
из (7.5)
№
Наименование закона
1.
Пропорциональный,
П-закон
2.
Интегральный,
И-закон
3.
Дифференциальный,
Д-закон
4.
Пропорциональноинтегральный,
ПИ-закон
k d  0, k p  0,
Пропорциональнодифференциальный,
ПД-закон
Интегральнодифференциальный,
ИД-закон
ki  0, k p  0,
5.
6.
k i  0, k d  0,
kp  0
k p  0, k d  0,
ki  0
Закон управления
u (t )  k p ·  (t )
t
u (t )  k i ·   ( )d
0
k p  0, k i  0,
kd  0
ki  0
u (t )  k d ·
d
dt
t
u(t )  k p ·  (t )  k i ·   ( )d
0
kd  0
k p  0, k i  0,
kd  0
d
u (t )  k p · (t )  k d ·
dt
t
u (t )  k i ·   ( )d  k d ·
0
d
dt
t
7.
Пропорциональноинтегральнодифференциальный,
ПИД-закон
k p  0, ki  0,
kd  0
u (t )  k p ·  (t )  k i ·   ( )d 
0
d
 kd ·
dt
6. Контрольные вопросы
1.
2.
3.
4.
5.
6.
7.
8.
Зачем вводят дифференцирующую составляющую в линейный
закон управления?
Каковы преимущества ПИД-закона управления?
Каковы недостатки ПИД-закона управления?
В каком случае следует рассматривать целесообразность использования ПИД-закона управления?
Какие линейные законы управления Вы знаете?
Зачем нужны более совершенные (по сравнению с линейными
законами) алгоритмы управления?
Почему в общепромышленных регуляторах не используются
различные комбинации кратных интегралов и производных высоких порядков, предусмотренные общей формой линейного закона управления?
Каким образом можно получить какой-либо линейный закон управления из обобщенной формы непрерывного ПИД-закона управления?
115
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 8
ТЕМА: «НЕЛИНЕЙНЫЕ ЗАКОНЫ УПРАВЛЕНИЯ»
Время проведения практического занятия (аудиторные часы) – 4 часа, занятие должно проводиться с компьютерным сопровождением в связи с обширностью материала.
Время самостоятельной работы студента (дополнительные часы) – 4 часа.
Цель занятия: изучить типовые нелинейные законы управления
(функциональные, логические, оптимизационные, параметрические), получить представления о базовых свойствах САУ с регуляторами этих видов.
Рассматриваемые вопросы:
1. Классификация нелинейных законов управления.
2. Примеры нелинейных законов управления и свойства САУ, в которых они используются.
1. Цели введения нелинейностей в закон управления
Пусть известно, что выход объекта управления y(t) порожден входным сигналом f(t). Если система линейна, то форма выходного сигнала
сохранится, если сохраняется форма входного сигнала (изменится лишь
масштаб). Это свойство линейных систем не всегда является желательным. Можно привести примеры из нашего собственного опыта: на небольшие возмущения мы вообще никак не реагируем, и такая реакция
целесообразна и экономична. В данном примере не удастся рассчитать
реакцию на малые возмущения простым изменением масштаба реакций
на крупные воздействия.
Цели введения нелинейностей – сделать мир автоматических систем
более многообразным и, следовательно, расширить сферу их применения.
2. Классификация нелинейных законов управления (НЗУ)
Разновидности нелинейностей, которые могут быть использованы в
системах управления, неисчислимы. Но традиционно выделяют 4 группы
нелинейных законов:
1) функциональные;
2) логические;
3) оптимизирующие;
4) параметрические.
3. Функциональные нелинейные законы управления
3.1. Общая форма и классификация функциональных НЗУ
Обозначим: (t) = g(t) – y(t) – рассогласование между задающим воздействием g(t) и выходом объекта y(t); u(t) – управляющее воздействие
(все обозначенные переменные – скаляры).
116
Форма функционального нелинейного закона управления – непосредственное обобщение формы линейного закона управления (формула
(5.1) в практическом занятии № 5): аргументы те же, но их комбинации –
произвольные сочетания (не обязательно суммы, как в линейном законе
управления):
t
u (t )  f [ (t ),
Нелинейная функция
t 
d d 2
,
, ...,  ( )d , (  ( )d )d , ...].
dt dt 2


0
0 0
(8.1)
Рассогласование между
задающим воздействием
и выходом объекта
Форма зависимости управляющего воздействия от аргументов в (8.1)
может быть самой разнообразной, но различают два класса этой зависимости:
1. Класс 1: управляющее воздействие – простая нелинейная функция (не оператор!); как и для всякой простой (в математическом
смысле) функции, управляющее воздействие может быть вычислено по текущему значению рассогласования (t). Такой класс
функциональных нелинейных законов управления называется
статическими НЗУ. Для статических НЗУ
(8.2)
u(t )  f ( (t )) .
2. Класс 2: управляющее воздействие – нелинейный оператор над
значениями рассогласования; в этом случае управляющее воздействие зависит не только от текущего значения рассогласования,
но и от предыстории процесса управления, согласно общей формуле (8.1). Такой класс функциональных нелинейных законов
управления называется динамическими НЗУ.
3.2. Откуда возникла идея использования нелинейных функциональных законов управления?
Поясним основную идею введения нелинейности на простейшем
примере. Обратимся к изученным (практическое занятие № 5) свойствам
линейного пропорционального (П) регулятора. Рассмотрим, какие формы
может принять график отработки ступенчатого задающего воздействия
при различных значениях настроечного параметра регулятора kp (будем
полагать, что возмущения отсутствуют, а для устранения статической
ошибки воспроизведения задания используем корректирующий множитель, введенный в п. 4.5 практического занятия № 5). Возможные формы
зависимости (их только две) показаны на рис. 8.1.
При малых значениях kp выход объекта изменяется монотонно (т. е. без
изменения знака производной), перерегулирование не возникает (рис. 8.1а).
117
Будем увеличивать kp. При некотором значении монотонность нарушится и
появится перерегулирование. Выход объекта приобретет форму апериодического (знак производной изменится однократно) или колебательного
процесса (знак производной изменяется многократно), как на рис. 8.1б.
а)
б)
Рис. 8.1. Две формы графика отработки ступенчатого задающего воздействия:
а) без перерегулирования, б) с перерегулированием
Зададим себе вопрос: «Какой из процессов, показанных на рис. 8.1,
лучше?» Однозначно ответить нельзя: у монотонного процесса гораздо
более спокойный и полезный для технологического процесса финиш, но
затянутый во времени старт. У колебательного процесса, наоборот, гораздо более «резвый», полезный для технологического процесса старт, но
неблагоприятный (а для некоторых технологических процессов вовсе недопустимый) финиш с перерегулированием.
Пришло время ответить на вопрос: «Зачем совершенствовать линейные законы управления?» Представим себе идеал: старт, как у процесса,
показанного на рис. 8.1б, а финиш – как у монотонного, представленного
на рис. 8.1а. Получим «синтетический идеал», процесс-мечту, показанный
на рис. 8.2.
Ответ на вопрос зачем? получен: попытаться найти закон управления, который обеспечил бы эффективное сочетание быстрой начальной
фазы процесса отработки задания со спокойным характером приближения к заданию в концевой фазе процесса.
Разберем причины, по которым график, показанный на рис. 8.2, недостижим в линейных системах (ответ на вопрос почему?). Мы уже ответили на этот вопрос выше: формы процессов в линейных системах воспроизводятся, поэтому можно получить только либо левый, либо правый
вариант форм графиков, показанных на рис. 8.1, но никак не сочетание
этих графиков.
118
Идеальный «синтетический» процесс:
старт, как у колебательного,
финиш, как у монотонного процесса
Желателен старт, как у колебательного
процесса, рис. 8.1б
Желателен финиш, как у монотонного
процесса, рис. 8.1а
Рис. 8.2. Желательный график отработки ступенчатого задающего воздействия
Теперь мы подошли к поиску ответа на вопрос как? Можно догадаться, что если бы настроечный параметр П-регулятора kp зависел от
величины рассогласования (t) и убывал бы по мере подхода к заданию, то появилась бы надежда получить график, как на рис. 8.2. Но как
только мы сказали, что kp должен зависеть от (t) – мы сразу вышли за
границы линейности: такой закон управления окажется нелинейным.
Для ответа на вопрос как? осталось просто придумать варианты этой зависимости.
3.3. Примеры функциональных нелинейных законов управления
и их свойства
Пример 1. Статические нелинейные регуляторы. Закон управления:
(8.3)
u(t )  k p · (1  k n · |  (t ) |) ·  (t ),  (t )  g (t )  y(t ) ,
где kn – настроечный параметр, с помощью которого регулируется степень участия нелинейности в законе управления.
Структура закона управления такова: сомножитель kp ∙ (1 + kn∙ |(t)|)
играет роль эквивалентного коэффициента усиления П-регулятора. Значение этого коэффициента зависит от величины рассогласования (t)
между задающим воздействием g(t) и выходом объекта y(t). При больших
(по абсолютной величине) рассогласованиях эквивалентный коэффициент увеличен. При подходе к заданию, когда абсолютная величина рассогласования уменьшается, эквивалентный коэффициент усиления также
уменьшается. Благодаря этому для нелинейного закона управления можно выбрать коэффициент настройки kp меньшим, чем для линейного закона (таким, при котором в САУ с линейным П-регулятором не будет перерегулирования).
119
Аналогичные эффекты можно получить, если использовать квадрат
рассогласования вместо абсолютной величины:
(8.4)
u (t )  k p · [1  k n ·  2 (t )] ·  (t ) .
Полезный эффект введения нелинейности иллюстрирует рис. 8.3.
САУ с нелинейным регулятором,
закон управления – по формуле (8.4)
Рис. 8.3. Сравнение качества управления в САУ с линейным П-регулятором и нелинейным
статическим регулятором (8.4)
Мы видим, что в начальной фазе переходного процесса скорость изменения выхода в САУ с нелинейным регулятором практически такая же
высокая, как в САУ с П-регулятором. По мере подхода к заданию эквивалентный коэффициент усиления нелинейного регулятора уменьшается,
благодаря чему практически устраняется перерегулирование и обеспечивается плавное приближение к заданию в концевой фазе переходного процесса.
Пример 2. Динамический нелинейный регулятор. Введем нелинейности в линейный пропорционально-интегральный (ПИ) (формула (6.10))
закон управления:
du
d
(8.5)
 k p · (1  k n1 · |  (t ) |) ·
 k i · (1  k n 2 · |  (t ) |) ·  (t ) .
dt
dt
Цели введения нелинейностей – те же, что и в примере 1. Настроечные параметры kn1, kn2 позволяют регулировать степень участия нелинейных добавок в пропорциональной и интегральной составляющих ПИрегулятора соответственно (в линейном ПИ-регуляторе степень участия
П- и И-составляющих задается параметрами kp, ki соответственно).
Эффект введения нелинейностей в ПИ-закон управления показан на
рис. 8.4.
120
Рис. 8.4. Сравнение качества управления в САУ с линейным ПИ-регулятором и в САУ с
нелинейным динамическим регулятором (8.5). Система программного управления
На практическом занятии № 6 мы отмечали, что ПИ-регулятор не
всегда обеспечивает нужное качество управления в системах программного управления (в частности, если задающее воздействие высокочастотное). На рис. 8.4 показан именно такой случай: линейный ПИ-регулятор
отрабатывает меандровое задающее воздействие с большими перерегулированиями. За счет введения нелинейностей удается существенно
улучшить качество воспроизведения задания без ущерба для быстродействия системы.
В следящих системах за счет введения нелинейностей также удается
значительно улучшить качество воспроизведения задающего воздействия
(рис. 8.5).
САУ с нелинейным динамическим регулятором,
закон управления – по формуле (8.5)
Рис. 8.5. Сравнение качества управления в САУ с линейным ПИ-регулятором и в САУ с
нелинейным динамическим регулятором (8.5). Следящая система
Другие варианты введения нелинейностей и их эффекты
Заметим, что идея введения нелинейностей предоставляет пытливым
инженерам и студентам огромные возможности для изобретений (мир нелинейностей бесконечно многообразен). Приведем несколько примеров.
121
1. Введение дополнительной нелинейности в релейный регулятор (который, естественно, сам по себе реализует функциональный нелинейный закон управления). Рассмотрим процесс в САУ с «классическим»
релейным регулятором: управляющее воздействие определяется по знаку
(а не по величине) рассогласования между задающим воздействием и выходом объекта. В такой САУ неизбежны автоколебания. Закон управления имеет вид:
1 k · k

o
r
(8.6)
u (t )  k r · sign 
· z (t )  y (t )  ,
 ko · k r



где ko – коэффициент усиления объекта, kr – настроечный параметр релейного регулятора, z(t), y(t) – соответственно задающее воздействие и
выход объекта.
Сомножитель 1 k o · k r введен для компенсации статической
ko · kr
ошибки воспроизведения задания (см. п. 4.5 практического занятия № 5).
Нелинейность введена функцией sign(…):
 0, если (...)  0

sign (...)   1, если (...)  0 .
 1, если (...)  0

На рис. 8.6 показан процесс отработки переменного во времени задающего воздействия (система программного управления).
а)
б)
Рис. 8.6. Процессы в САУ с релейным регулятором: а – отработка переменного во
времени задающего воздействия (kr = 0.8); б – фрагмент графика изменения управляющего
воздействия
122
Мы видим, что управляющее воздействие (в зависимости от знака
рассогласования между заданием и выходом объекта) принимает одно из
двух возможных значений. Управляющие воздействия изменяются резко,
что не всегда желательно (может вызвать повышенный износ технических средств управления). Из-за резких изменений управляющих воздействий характер воспроизведения задания получается волнообразным.
Введем корректирующую нелинейность, ослабляющую значения
управлений, если выход объекта близок к заданию:
1  k · k · k

o
r
n
u (t )  k r · sign 
· z (t )  y (t ) 
 ko · k r · k n



1  ko · k r · k n
(8.7)
 1  k n ·
· z (t )  y (t )  .


ko · k r · k n


За счет введения нелинейности можно значительно уменьшить kr по
сравнению со значением в (8.6). Ожидаемые эффекты от введения корректирующей нелинейности: во-первых, управляющие воздействия будут
изменяться малыми ступеньками переменной величины, поэтому график
выхода объекта станет более гладким; во-вторых, благодаря возможности
уменьшить kr диапазон изменения управляющих воздействий будет
меньшим, чем в САУ с регулятором (8.6). Эти эффекты подтверждают
рис. 8.7 и 8.8.
Рис. 8.7. График выхода объекта в САУ с релейным регулятором с корректирующей
нелинейностью (kr = 0.05; kn = 60)
123
Управляющее воздействие
Величина «ступеньки» изменения
управляющего воздействия не
постоянна, а зависит от величины
рассогласования между выходом
и заданием
Рис. 8.8. Фрагмент графика изменения управляющего воздействия в САУ с релейным
регулятором с корректирующей нелинейностью
2. Динамический пропорционально-дифференциальный регулятор с форсированной или с демпфированной реакцией на быстрое изменение рассогласования между заданием и выходом объекта. Закон управления имеет вид:

d 
(8.8)
u (t )  k p · 1  kd ·
 ·  (t ) ,
dt


где kp, kd – настроечные параметры, (t) – рассогласование, знак (+) приводит к форсировке реакции на быстрое изменение рассогласования, а
знак (–) – к ее демпфированию, подавлению.
4. Логические нелинейные законы управления
4.1. Происхождение и определение логических НЗУ
Если не удается обеспечить хорошее качество управления при использовании известных законов управления, часто прибегают к протоколированию действий опытного оператора. Получается своего рода рецептурный справочник: если ситуация такова, то делай так… (похоже на
устав военной службы). Формализация таких рецептов содержит логические функции (ЕСЛИ, И, ИЛИ, НЕ, ИСКЛЮЧАЮЩЕЕ ИЛИ, …).
Определение: Группа алгоритмов, построенная с использованием
логических функций, называется логическими нелинейными законами управления (в этом определении слово «нелинейными» лишнее: логические функции сами по себе нелинейны).
На базе подражания опытным диспетчерам сформировалась целая
ветвь теории управления (так называемое ситуационное управление).
Популярность этого направления непрерывно растет, в особенности благодаря появлению нейронных сетей, способных обучаться.
124
4.2. Пример САУ с логическим нелинейным законом управления. Регулятор LittleMan
Рассмотрим задачу управления уровнем воды в водохранилище
(рис. 8.9).
Река
Аварийный сброс
Водохранилище
Отводящий канал
Многопролетное
гидротехническое
сооружение
Рис. 8.9. Схема технологического комплекса
Технологический комплекс состоит из следующих элементов:
1. Водохранилище с водозаборным узлом, расположенное в месте
впадения реки – источника воды.
2. Отводящий канал, по которому вода из водохранилища подается
в оросительную систему.
3. Аварийный сброс, по которому отводится вода при переполнении водохранилища выше предельной отметки.
4. Гидротехническое сооружение, с помощью поднимания / опускания затворов которого регулируется подача воды в отводящий
канал и аварийный сброс.
Технологическая цель комплекса – обеспечить подачу воды в отводящий канал согласно заявке потребителей.
Необходимость системы управления объясняется тем, что график
подачи воды потребителям не связан жестко с поступлением воды по реке. Различия частично погашаются запасом воды в водохранилище.
Регулятор LittleMan предназначен для поддержания уровня воды в
водохранилище в заданном диапазоне. Заданы: верхняя Hmax (м) и нижняя Hmin (м) отметки уровня воды в водохранилище. Требуется управлять
объектом так, чтобы текущее значение уровня воды H(t) практически
всегда было между этими отметками: Hmin  H(t)  Hmax. Небольшие периоды выхода за эти отметки допустимы, т. к. значения Hmax и Hmin устанавливаются с запасом.
Алгоритм LittleMan следует логике очень ленивого диспетчера. Рассмотрим график изменения уровня воды в водохранилище (рис. 8.10).
125
Рис. 8.10. График изменения уровня воды в водохранилище с указанием характерных
режимов
Мы видим, что благодаря довольно широкому диапазону допустимых значений уровня режим, в основном, таков, что никакого вмешательства не требуется.
Но в некоторые периоды уровень воды выходит за желательные пределы. Ленивая логика регулятора такова, что ЕСЛИ уровень выходит за
допустимый предел, НО «сам по себе» стремится вернуться в допустимый диапазон, то ничего делать не нужно (ситуация сама исправится). И
только в случае развития неблагоприятной ситуации нужно вмешаться.
Алгоритм таков:
Задаться дискретой времени (чаще всего 15 минут).
Для каждой дискреты t выполнять:
ЕСЛИ Hmin  H(t)  Hmax, то НИЧЕГО НЕ ДЕЛАТЬ.
ИНАЧЕ ЕСЛИ H(t) > Hmax И dH
(т. е. если уровень убывает), ТО НИЧЕГО НЕ ДЕЛАТЬ.
0
dt
ИНАЧЕ ЕСЛИ H(t) < Hmin И dH
(т. е. если уровень растет), ТО НИЧЕГО НЕ ДЕЛАТЬ.
ИНАЧЕ ЕСЛИ H(t) > Hmax
0
dt
И dH
(т. е. если уровень не убывает), ТО ОТКРЫТЬ ЗА0
dt
ТВОР АВАРИЙНОГО СБРОСА. ПОДОЖДАТЬ 3 – 4 ТАКТА
ИНАЧЕ ЕСЛИ H(t) < Hmin И dH  0 (т. е. если уровень не возрастает), ТО ЗАКРЫТЬ ЗАdt
ТВОР ОТВОДЯЩЕГО КАНАЛА. ПОДОЖДАТЬ 3 – 4 ТАКТА
КОНЕЦ ЕСЛИ
Человек, наблюдающий за работой LittleMan’а, может потратить не
одни сутки, пока дождется, чтобы регулятор «проснулся» и выполнил работу. Надежность регулятора очень высока, износ почти не происходит –
тем не менее уровень воды в водохранилище поддерживается хорошо.
126
4.3. Где используются логические регуляторы?
Область применения – плохо формализуемые задачи управления.
Один из примеров задач такого типа – управление подходом судов к
причалам на разгрузку в порту с напряженным ритмом работы.
5. Оптимизирующие нелинейные законы управления
5.1. Общие замечания
В п. 2 практического занятия № 5 мы упоминали о двух подходах к
созданию алгоритмов управления – изобретательскому (ему и были посвящены занятия № 5, 6, 7) и критериальному, существо которого – в получении алгоритма «на кончике пера» по следующей схеме:
1. Исходя из цели и содержательной постановки задачи управления
объектом, формулируется критерий, характеризующий качество
управления.
2. Записываются ограничения, которым должен удовлетворять
процесс управления.
3. Формализуется модель объекта и технических элементов системы управления.
В результате получается формализованная, математическая задача: для заданной модели объекта создать алгоритм управления, доставляющий наилучшее значение критерию качества при выполнении
ограничений, накладываемых на процесс управления.
Определение. Алгоритм управления, синтезированный в результате
решения этой задачи, может оказаться как линейным, так и нелинейным. В последнем случае такой алгоритм относится к классу нелинейных оптимизирующих законов управления.
Отметим, что задача синтеза оптимизирующего алгоритма управления является одной
из задач математической теории вариационного исчисления; в ней используется тройка
понятий: {критерий, ограничения, модель объекта}. Некоторые вопросы вариационного
исчисления изучаются в учебной дисциплине «Методы оптимизации», входящей в план
подготовки инженеров по специальности «Автоматизированные системы обработки информации и управления».
В п. 2 практического занятия № 5 мы также отмечали, что критериальный подход к созданию алгоритмов управления применяется, в основном, в индивидуальных, ответственных проектах систем управления (в
отличие от линейных П-, ПИ-, ПИД-законов управления, встраиваемых в
общепромышленные регуляторы для массового использования). Это объясняется двумя причинами:
 Во-первых, тем, что постановки задач оптимизации обычно сложны, требуют тщательного учета особенностей объекта управления
и не всегда могут быть решены на базе методов, известных к моменту разработки системы (требуют развития этих методов). Для
развития новых методов требуется проведение научных исследований, но нет гарантии, что затраченное на них время приведет к
127
успеху (а при проектировании сроки создания системы жестко
ограничены). Поэтому приходится прибегать к «натяжкам»: выбирать критерий, модель объекта и ограничения, не точно соответствующие содержательной постановке, но подпадающие под уже
разработанные методы синтеза алгоритмов.
 Во-вторых, тем, что по самому существу задачи оптимизации алгоритм управления будет «выжимать» все ресурсы управления ради
того, чтобы доставить экстремум критерию. В результате может
оказаться, что алгоритм будет обладать плохими показателями
чувствительности: небольшие (неизбежные) неточности в модели
объекта и ограничениях могут привести к большим потерям качества управления. В занятии № 5 мы отмечали, что показатели чувствительности линейных алгоритмов хорошие (см., например, п.
4.7).
Но всё же в случае успеха оптимизирующие алгоритмы позволяют
получить качество управления намного превосходящее достижимое
при использовании изобретенных алгоритмов.
5.2. Замечания к постановкам задач синтеза оптимизирующих
алгоритмов управления
Задача синтеза состоит в разработке структуры САУ и определении
параметров алгоритма управления, обеспечивающих достижение требуемых показателей качества управления. Классы внешних и внутренних
возмущений, а также модель объекта остаются известными (возможно,
сведения о модели предлагаются известными неточно – например, структура модели известна, а параметры неизвестны).
5.2.1. Понятие о «трубке Солодовникова». По существу практическая задача синтеза почти всегда является многокритериальной, т. к. показатели качества САУ противоречивы и требуется добиться компромисса между ними. В частности, при изучении линейных законов управления
мы отмечали, что требование обеспечить минимальное время переходного процесса вступает в конфликт с требованием обеспечить отсутствие
перерегулирования. Понятие «трубка Солодовникова» используется для
того, чтобы алгоритм обеспечил компромисс между противоречивыми
показателями качества управления. Алгоритм управления должен быть
таким, чтобы все инженерные показатели качества управления не выходили за границы, оговоренные в техническом задании на разработку системы управления.
5.2.2. Общая формулировка задачи синтеза оптимизирующего алгоритма. Найти структуру системы управления и определить последовательность управляющих воздействий U(t), 0  t  T (Т задано), обеспечивающих экстремум критерия качества J (в математической теории оптимизации он называется функционалом), J = J(y(t), u(t), t, 0  t  T) при
выполнении ограничений на переменные состояния Ymin  y(t)  Ymax и
128
управляющие воздействия Umin  u(t)  Umax  t [0, T] и удовлетворяющих математической модели объекта (трактуемой как совокупность
ограничений-равенств).
Постановка задачи следует общей математической логике вариационного исчисления. Конкретные конструктивные решения получены только
для частных случаев функционалов, ограничений и моделей объекта.
5.2.3. Типизация критериев оптимальности САУ и сведения о разработанных методах синтеза. Наиболее значимые результаты получены
для следующих критериев:
1. Быстродействие САУ (задача об оптимальном быстродействии, решается на основе принципа максимума Л. С. Понтрягина).
2. Суммарное среднее квадратическое отклонение воздействий от
заданных значений (задача об аналитическом конструировании оптимальных регуляторов, АКОР, решается на основе метода динамического программирования Р. Беллмана).
3. Суммарное среднее квадратическое отклонение векторов состояния и управляющих воздействий от оптимальных значений, достигаемых при минимизации критерия обобщенной работы (задача
решается в терминах теории устойчивости А. М. Ляпунова).
4. Минимизация максимального отклонения объекта от заданного
значения (задача о минимаксе, решается в терминах чебышевской задачи линейного программирования.)
5. Воспроизведение желательной формы логарифмической амплитудной частотной характеристики САУ (задача решается в терминах частотного синтеза последовательных корректирующих устройств, дополняющих структуру САУ).
6. Воспроизведение эталонного поведения системы в условиях неполной информации о параметрах модели объекта (задача решается в
терминах синтеза адаптивных систем с эталонной моделью).
5.3. Пример оптимизирующего нелинейного закона управления
Рассмотрим постановку задачи синтеза алгоритма управления, обеспечивающего минимум времени переходного процесса (задача об оптимальном быстродействии).
Замечание. Полезно обратиться к опыту экстремального автомобильного спорта.
Представим себе, каким образом любитель экстремальной езды управлял бы автомобилем,
если бы ему нужно было проехать по очень хорошей дороге от заданного начального пункта к заданной точке остановки за минимальное время. Высококлассный водитель ведет себя
так: сразу включает максимально возможную скорость, а затем в точно рассчитанный момент времени включает максимальное торможение.
Задача об оптимальном быстродействии была поставлена в 1952 г.
одним из наиболее талантливых советских ученых А. А. Фельдбаумом и
решена им для одного частного случая, который мы и рассмотрим. В общем виде эта задача была решена математиками: академиком Л. С. Понт129
рягиным и его школой. Результат был сформулирован в теореме, получившей название «Принцип максимума Л. С. Понтрягина».
Рассмотрим следующую задачу: пусть модель объекта класса «входвыход» задана в форме дифференциального уравнения n-го порядка, причем соответствующее характеристическое уравнение имеет только действительные корни, среди которых нет кратных:
a0 ·
dny
d n 1 y
dy
 a1 ·
   an 1·
 an · y(t )  k · u (t ) ,
n
n 1
dt
dt
dt
(8.9)
где y(t), u(t) – соответственно выход объекта и управляющее воздействие
(скаляры), k – коэффициент усиления объекта, a0, … , an – параметры.
Управляющие воздействия ограничены по диапазону:
(8.10)
U min  u(t )  U max .
Требуется найти u(t), переводящее систему из заданного начального
состояния в заданное конечное состояние за минимальное время.
В данной задаче имеются все три признака задачи оптимизации: модель объекта (8.9) – линейная, имеются ограничения (8.10) и задан критерий – время переходного процесса.
Эта задача была поставлена и решена А. А. Фельдбаумом. Решение
сформулировано в форме теоремы об n интервалах: график управляющего воздействия состоит из переключений с одного граничного значения управления к другому; число таких переключений равно порядку
дифференциального уравнения (8.9), а продолжительность каждого интервала постоянства управляющего воздействия уменьшается – от наиболее продолжительного первого интервала к наиболее кратковременному
последнему интервалу. Пример графика управляющего воздействия показан на рис. 8.11.
Рис. 8.11. График управляющего воздействия в системе, оптимальной по быстродействию
130
Мы видим, что в данном случае управление получилось релейным (т. е.
нелинейным), несмотря на то, что модель объекта (8.9) линейная. Нелинейность закона управления объясняется наличием ограничений (8.10) и
нелинейной зависимостью критерия (быстродействие) от переменных состояния и управляющих воздействий.
6. Параметрические нелинейные законы управления
Определение: параметрическим законом управления называется такой, в котором управляющее воздействие зависит от некоторого параметра (а не от выхода объекта!).
Так же, как и оптимизирующие, параметрические законы управления
не относятся к типовым, синтезируются индивидуально, с учетом конкретных особенностей прикладной задачи.
6.1. Пример параметрического закона управления
Рассмотрим задачу стыковки космического корабля с орбитальной
станцией, рис. 8.12.
Рис. 8.12. Графическая интерпретация задачи преследования
Сформулируем естественные требования к алгоритму управления.
Эти требования будут определены не в зависимости от переменных состояния объекта (преследователя), а в терминах внешнего параметра –
расстояния  от преследователя до цели.
1. Требование 1: объекты должны сближаться, т. е. расстояние (t)
должно быть убывающей функцией времени; математически это
означает, что производная расстояния во времени отрицательна:
d
 0.
dt
2. Требование 2: контакт преследователя и цели должен быть мягким, т. е. в момент причаливания скорость изменения расстояния
d
должна быть нулевой:
0.
dt  0
3. Требование 3: сила удара в момент причаливания должна быть
не больше допустимой; согласно 2-му закону Ньютона сила удара
пропорциональна ускорению, поэтому данное требование ограни-
131
d 2
 Bmax , где Bmax –
dt 2
максимально допустимая (по абсолютной величине) сила удара.
4. Требование 4: время T достижения контакта должно быть не
больше заданного (то есть быть конечным): T  T *.
Начальное расстояние 0 от преследователя до цели задано.
Попытаемся задать такой закон изменения параметра , чтобы выполнить все требования. Наиболее простой способ – «заставить» управляющее воздействие изменять  согласно простейшему дифференциальd
 k ·   0 . Решение его имеет вид:
ному уравнению:
dt
 (t )  0 · e k ·t .
К сожалению, требование 4 не выполняется: время достижения контакта теоретически бесконечно.
Введем в закон изменения параметра нелинейность:
d
(8.11)
 k · b  0.
dt
Если подобрать управляющее воздействие таким, чтобы расстояние
между преследователем и целью изменялось по закону (8.11), то получим, решая (8.11) при разных значениях показателя степени b:
 При b  1 время причаливания T∞, не выполняется требование 4.
чивает вторую производную расстояния:
 При b < 0.5 сила удара недопустима:
d 2
dt 2
  , не выполняется
требование 3.
 При 0.5  b < 1 все требования выполняются. Этот вариант и
приведет к успеху.
Концевой участок изменения расстояния от преследователя до цели
показан на рис. 8.13.
132
Рис. 8.13. Изменение расстояния от преследователя до цели при разных значениях b
Мы видим, что при b = 0.7 время причаливания конечно, все требования к закону изменения параметра выполняются.
7. Заключение
Еще раз повторим: мир нелинейных законов управления неисчерпаем и поэтому может оказаться хорошим полигоном как для тех, кто любит изобретать, так и для тех, кто склонен к аналитической работе.
8. Контрольные вопросы
Какова цель введения нелинейностей в закон управления?
Какие типы нелинейных законов управления Вы знаете?
Что такое функциональные нелинейные законы управления?
Какие функциональные нелинейные законы управления называются статическими?
5. Какие функциональные нелинейные законы управления называются динамическими?
6. Что такое логические нелинейные законы управления?
7. Какова область применения логических регуляторов?
8. Что такое оптимизирующие нелинейные законы управления?
9. Что означает понятие «трубка Солодовникова»?
10. Что такое параметрические нелинейные законы управления?
1.
2.
3.
4.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
133
1. Методы классической и современной теории автоматического управления: В 3-х т. /
Под ред. Н. Д. Егупова. – М.: МГТУ им. Н. Э. Баумана, 2000. – 748 с.
2. Бесекерский, В. А. Теория систем автоматического управления / В. А. Бесекерский,
Е. П. Попов. – М.: Профессия, 2004. – 752 с.
3. Ким, Д. П. Сборник задач по теории автоматического управления. Линейные системы / Д. П. Ким, Н. Д. Дмитриева. – М.: ФИЗМАТЛИТ, 2007. – 168 с.
4. Советов, Б. Я. Моделирование систем. Практикум / Б. Я. Советов, С. А. Яковлев. –
М.: ВШ, 2005. – 295 с.
5. Афанасьев, В. Н. Математическая теория конструирования систем управления /
В. Н. Афанасьев, В. Б. Колмановский, В. Р. Носов. – М.: ВШ, 1998. – 574 с.
6. Теория автоматического управления / Под ред. Ю. М. Соломенцева. – М.: ВШ,
2003. – 268 с.
7. Автоматизированные системы управления. Лабораторный практикум по техническим средствам / Под общ. ред. В. Н. Четверикова. – М.: ВШ, 1986. – 279 с.
8. Проектирование систем автоматического контроля, регулирования и управления
технологическими объектами в металлургии / В. В. Ласенко [и др.] – Волгоград: РПК «Политехник», 2006. – 136 с.
134
СОДЕРЖАНИЕ
ПРЕДИСЛОВИЕ …...…………………………………………………
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1. ТЕМА: «ЭТАПЫ РАБОТ
ПРИ СОЗДАНИИ САУ»…………………………………………….
1. Основные работы, выполнение которых необходимо для создания эффективной САУ …………………………………...
2. Пример: система управления нагревательной установкой ….
3. Необходимые теоретические сведения …..…………………..
4. Контрольные вопросы …………………………………………
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 2. ТЕМА: «СГЛАЖИВАНИЕ
ЭКСПЕРИМЕНТАЛЬНЫХ ЗАВИСИМОСТЕЙ. ОЦЕНКА
ПАРАМЕТРОВ МОДЕЛИ ОБЪЕКТА»…………………………...
1. Цель обработки экспериментальных данных ………………..
2. Метод скользящего среднего ………………………………….
3. Метод четвертых разностей …...………………………………
4. Сравнение методов скользящего среднего и четвертых разностей ……………………….…………………………………...
5. Оценка параметров модели объекта по сглаженной кривой
разгона …………………………………………………………...
6. Контрольные вопросы …………………………………………
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 3. ТЕМА: «ПОСТРОЕНИЕ
ПЕРЕДАТОЧНЫХ ФУНКЦИЙ. ПОНЯТИЕ ОБ УПРАВЛЕНИИ
С ОБРАТНОЙ СВЯЗЬЮ» …………………………………………...
1. Определение передаточной функции САУ..............................
2. Пример построения передаточной функции САУ по ее
дифференциальному уравнению ……………..……………….
3. Пример построения дифференциального уравнения САУ
по ее передаточной функции…………………………………...
4. Качественные особенности замкнутой САУ с обратной
связью. Существо управления с обратной связью ..…..……...
5. Контрольные вопросы …………………………………………
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 4. ТЕМА: «СТРУКТУРНЫЕ
ПРЕОБРАЗОВАНИЯ САУ С ПЕРЕКРЕСТНЫМИ СВЯЗЯМИ» …
1. Технология структурных преобразований САУ
с перекрестными связями ……………..………………………
2. Пример получения общей передаточной функции
многоконтурной САУ с перекрестными связями …..……….
3. О пользе передаточных функций для исследования САУ ….
4. Контрольные вопросы …………………………………………
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 5. ТЕМА: «КЛАССИФИКАЦИЯ
ЗАКОНОВ УПРАВЛЕНИЯ. ЛИНЕЙНЫЕ ЗАКОНЫ
УПРАВЛЕНИЯ. ПРОПОРЦИОНАЛЬНЫЙ РЕГУЛЯТОР»…....….
135
3
9
9
10
12
24
25
25
26
30
33
33
36
37
37
38
39
41
46
47
47
48
54
55
56
1. Классификация законов управления ………………………….
2. Линейные законы управления ……….………………………..
3. Кривая разгона П-регулятора …………………………………
4. Исследование свойств системы управления с П-регулятором .
5. Сводка свойств системы управления с П-регулятором ……..
6. Контрольные вопросы …………………………………………
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 6. ТЕМА: «ЛИНЕЙНЫЕ ЗАКОНЫ УПРАВЛЕНИЯ. ПРОПОРЦИОНАЛЬНО-ИНТЕГРАЛЬНЫЙ
РЕГУЛЯТОР» …………………………………..…………………...
1. Свойства И-регулятора ………………………………………..
2. Зачем усложнять структуру И-регулятора? Идея ПИ-регулятора………………………….......……………………………….
3. Структурная схема ПИ-регулятора, его кривая разгона,
закон управления и передаточная функция …………………..
4. Исследование свойств САУ с ПИ-регулятором ……………..
5. Сводка свойств системы управления с ПИ-регулятором …...
6. Нужны ли дальнейшие усложнения закона управления? …...
7. Как усовершенствовать ПИ-закон управления? ……………..
8. Контрольные вопросы …………………………………………
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 7. ТЕМА: «ЛИНЕЙНЫЕ ЗАКОНЫ УПРАВЛЕНИЯ. ПРОПОРЦИОНАЛЬНО-ИНТЕГРАЛЬНОДИФФЕРЕНЦИАЛЬНЫЙ РЕГУЛЯТОР» ……………………..…..
1. Структурная схема ПИД-регулятора, его кривая разгона,
закон управления и передаточная функция …………………..
2. Свойства САУ с ПИД-регулятором …………………………..
3. Сводка свойств системы управления с ПИД-регулятором …
4. Нужны ли дальнейшие усложнения закона управления? …...
5. Сводка изученных линейных законов управления ………….
6. Контрольные вопросы …………………………………………
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 8. ТЕМА: «НЕЛИНЕЙНЫЕ ЗАКОНЫ УПРАВЛЕНИЯ»………….…………………. ………………
1. Цели введения нелинейностей в закон управления …………
2. Классификация нелинейных законов управления (НЗУ) …...
3. Функциональные нелинейные законы управления ………….
4. Логические нелинейные законы управления ………………...
5. Оптимизирующие нелинейные законы управления ………...
6. Параметрические нелинейные законы управления ………….
7. Заключение ……………………………………………………..
8. Контрольные вопросы …………………………………………
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ …………………
136
56
57
59
60
74
74
75
75
79
80
82
95
96
102
103
104
104
107
113
114
114
115
116
116
116
116
124
127
131
133
133
133
Елена Георгиевна Крушель,
Наталия Александровна Панфилова
МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ
ПО ДИСЦИПЛИНЕ «ОСНОВЫ ТЕОРИИ УПРАВЛЕНИЯ»
Учебное пособие
Редактор Пчелинцева М. А.
Компьютерная верстка Сарафановой Н. М.
Темплан 2010 г., поз. № 16К.
Подписано в печать 18. 05. 2010 г. Формат 60×84 1/16.
Бумага листовая. Печать офсетная.
Усл. печ. л. 8,5. Усл. авт. л. 8,31.
Тираж 100 экз. Заказ №
Волгоградский государственный технический университет
400131, г. Волгоград, пр. Ленина, 28, корп. 1.
Отпечатано в КТИ
403874, г. Камышин, ул. Ленина, 5, каб. 4.5
137