Рисунок 4.15 – Вероятностная модель с фиксированной периодичностью

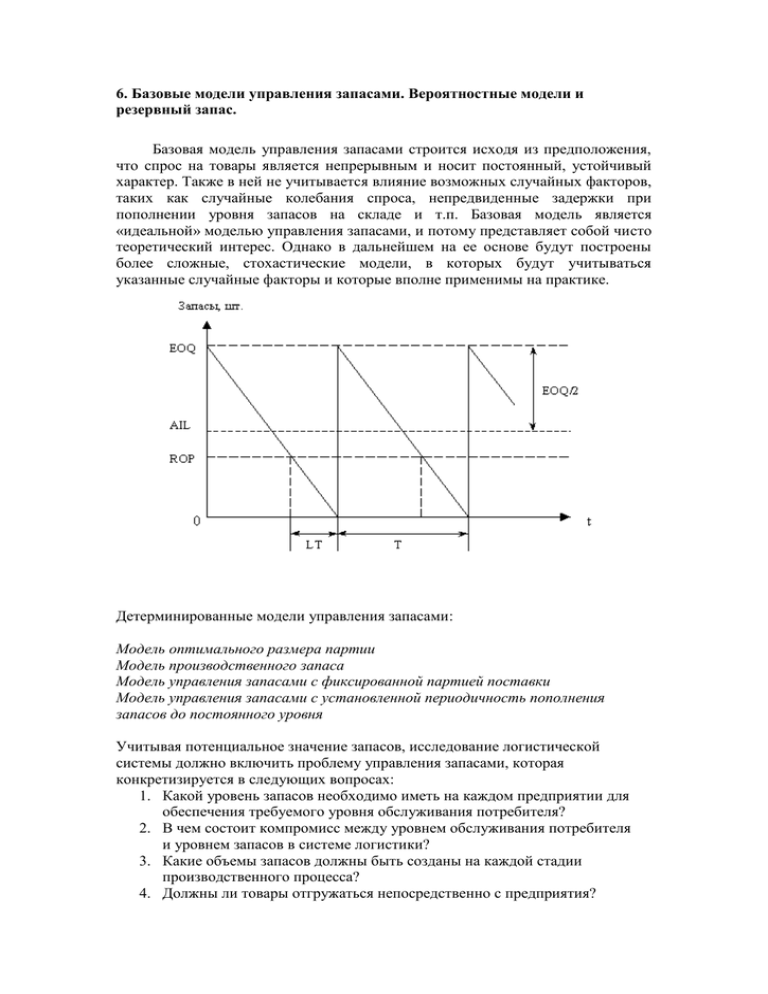
6. Базовые модели управления запасами. Вероятностные модели и
резервный запас.
Базовая модель управления запасами строится исходя из предположения,
что спрос на товары является непрерывным и носит постоянный, устойчивый
характер. Также в ней не учитывается влияние возможных случайных факторов,
таких как случайные колебания спроса, непредвиденные задержки при
пополнении уровня запасов на складе и т.п. Базовая модель является
«идеальной» моделью управления запасами, и потому представляет собой чисто
теоретический интерес. Однако в дальнейшем на ее основе будут построены
более сложные, стохастические модели, в которых будут учитываться
указанные случайные факторы и которые вполне применимы на практике.
Детерминированные модели управления запасами:
Модель оптимального размера партии
Модель производственного запаса
Модель управления запасами с фиксированной партией поставки
Модель управления запасами с установленной периодичность пополнения
запасов до постоянного уровня
Учитывая потенциальное значение запасов, исследование логистической
системы должно включить проблему управления запасами, которая
конкретизируется в следующих вопросах:
1. Какой уровень запасов необходимо иметь на каждом предприятии для
обеспечения требуемого уровня обслуживания потребителя?
2. В чем состоит компромисс между уровнем обслуживания потребителя
и уровнем запасов в системе логистики?
3. Какие объемы запасов должны быть созданы на каждой стадии
производственного процесса?
4. Должны ли товары отгружаться непосредственно с предприятия?
5. Каково значение компромисса между выбранным способом
транспортировки и запасами?
6. Каковы общие уровни запасов на данном предприятии, связанные
со специфическим уровнем обслуживания?
7. Как меняются затраты на содержание запасов в зависимости
от изменения количества складов?
8. Как и где следует размещать страховые запасы?
Перспективным вариантом решения проблем складирования является
«производство без складов», внедрение которого невозможно без кардинальных
изменений во всем комплексе процессов, обеспечивающих производство
и требующее значительных финансовых вложений. При этом необходимо было
решить несколько задач, среди которых, прежде всего, выделим задачу создания
высокоточной информационной системы по управлению запасами,
позволяющей использовать банк данных в реальном масштабе времени.
Логистическая система управления запасами проектируется с целью
непрерывного обеспечения потребителя каким-либо видом материального
ресурса. Реализация этой цели достигается решением следующих задач:
 учет текущего уровня запаса на складах различных уровней;
 определение размера гарантийного (страхового) запаса;
 расчет размера заказа;
 определение интервала времени между заказами.
Для решения проблем, связанных с запасами предназначены модели управления
запасами. Модели должны отвечать на два основных вопроса: сколько
заказывать продукции и когда. Есть множество разнообразных моделей, каждая
из которых подходит к определенному случаю, рассмотрим четыре наиболее
общих модели:
1. Модель с фиксированным размером заказа
2. Модель с фиксированным интервалом времени между заказами
3. Модель с установленной периодичностью пополнения запасов
до установленного уровня
4. Модель «Минимум — Максимум»
Модель с фиксированным уровнем запаса работает так: на складе есть
максимальный желательный запас продукции (МЖЗ), потребность в этой
продукции уменьшает ее количество на складе, и как только количество
достигнет порогового уровня, размещается новый заказ. Оптимальный размер
заказа (ОР) выбирается таким образом, чтобы количество продукции на складе
снова ровнялось МЖЗ, так как продукция не поставляется мгновенно,
то необходимо учитывать ожидаемое потребление во время поставки. Поэтому
необходимо учитывать резервный запас (РЗ), служащий для предотвращения
дефицита.
Для определения максимального желательного запаса (МЖЗ) используется
формула:
МЖЗ = ОР + РЗ.
Модель с фиксированным интервалом времени между заказами работает
следующим образом: с заданной периодичностью размещается заказ, размер
которого должен пополнить уровень запаса до МЖЗ.
Модель с установленной периодичностью пополнения запасов
до установленного уровня работает следующим образом: заказы делаются
периодически (как во втором случае), но одновременно проверяется уровень
запасов. Если уровень запасов достигает порогового, то делается
дополнительный заказ.
В зафиксированные моменты заказов расчет размера заказа производится
по следующей формуле:
РЗ = МЖЗ – ТЗ + ОП,
где,
РЗ — размер заказа, шт.;
МЖЗ — желательный максимальный заказ, шт;
ТЗ — текущий заказ, шт;
ОП — ожидаемое потребление за время.
В момент достижения порогового уровня размер заказа определяется
по следующей формуле:
РЗ = МЖЗ – ПУ + ОП,
где,
РЗ — размер заказа, шт.;
МЖЗ — максимальный желательный заказ, шт.;
ПУ — пороговый уровень запаса, шт.;
ОП — ожидаемое потребление до момента поставки, шт.
Модель «Минимум — Максимум» работает следующим образом: контроль
за уровнем запасов делается периодически, и если при проверке оказалось, что
уровень запасов меньше или равен пороговому уровню, то делается заказ.
При ближайшем рассмотрении этих моделей видно, что первая модель довольно
устойчива к увеличению спроса, задержке поставки, неполной поставке
и занижение размера заказа. Вторая модель устойчива к сокращению спроса,
ускоренной поставке, поставке завышенного объема и завышенного размера
заказа. Третья модель объединяет все плюсы двух первых моделей.
Для получения ответа на вопросы: когда и сколько заказывать материалов,
необходимо рассчитать объем резервного запаса и оптимального размера заказа.
При расчете объема резервного запаса (РЗ) рассматривается два случая: спрос
на продукцию (Tд) — детерминированная или случайная величина. В первом
случае: PЗ = Пд x Tзп, где Tзп — время возможной задержки поставки.
Во втором, время поставки и время возможной задержки поставки —
детерминированы. Значит ежедневный спрос за предыдущий период
определяется как математическое ожидание и дисперсия . Время между
моментом размещения заказа и моментом его получения (Q): Q = Tп + Tзп.
Спрос за время равен сумме ежедневных спросов, если более 4-х дней,
то суммарный спрос распределен по нормальному закону с математическим
ожиданием M(Пq) = Q * M(Пд), и дисперсией D(Пq) = Q * M(Пд).
Зададимся вероятностью возможного дефицита
, по таблице нормального
распределения находим
, значит
Таким образом, находим уровень резервного запаса из условия, что вероятность
возможного дефицита будет не более заданного.
Оптимальный размер заказа находится по формуле Уилсона:
где,
К- затраты на размещение одного заказа;
h — издержки на хранение 1 ед. продукции в ед. времени.
Выше были рассмотрены однопродуктовые модели. В реальных ситуациях
заказы делаются не на отдельные виды продукции, а на множество с одними
транспортными расходами. При переходе к многопродуктовой ситуации
расчеты резервного запаса и оптимального размера заказа не меняются. В этих
случаях более жизненными являются вторая и третья модели.
Детерминированные модели управления запасами, рассмотренные
нами выше, предполагали, что потребность в хранимых изделиях
известна и постоянна (обратите внимание на вторую графу таблицы 4.1).
На практике в большинстве случаев потребность является переменной
величиной, изменяясь ежедневно. В связи с эти необходимо иметь и
поддерживать так называемый резервный (буферный) запас,
обеспечивая определенный уровень защиты от дефицита изделий.
Резервный
запас
это
величина
запаса,
постоянно
поддерживаемая дополнительно к ожидаемой потребности.
В случае нормального распределения колебаний спроса это будет
среднее значение отклонений. Если, например, среднемесячная
потребность составляет 100 изделий, и мы предполагаем, что в
следующем месяце она останется такой же, а запас составляет 120
единиц, то 20 единиц и будут резервным запасом.
Известны несколько подходов к установлению величины запаса,
обеспечивающего защиту от колебаний спроса. Один из них
основывается на определении ожидаемого количества изделий, которых
может не хватить. Например, можно поставить задачу так: установить
такой уровень запаса, чтобы можно было удовлетворить не менее чем
95% заказов на данную продукцию, т.е. дефицит изделий будет
существовать лишь в течение 5% всего времени. Таким образом, мы
подошли к определению понятия "уровень обслуживания".
Уровень обслуживания – доля (процент) от общей величины
спроса, которую можно реально получить из наличного запаса.
Если, например, годовая потребность в некотором изделии
составляет 1000 шт., то 95%-ый уровень обслуживания означает, что 950
шт. можно получить из запаса, а 50 шт. не хватит.
Концепция уровня обслуживания основана на статистической
характеристике, известной как "Ожидаемое z или E(z)". E(z) – это
ожидаемое количество изделий, которых будет не хватать на
протяжении каждого интервала времени выполнения заказа.
Концепция предполагает, что потребность в хранимой продукции
является нормально распределенной случайной величиной.
Чтобы определить уровень обслуживания, необходимо знать,
сколько изделий не хватит.
Предположим, что среднемесячная потребность в каком-либо
изделии составляет 100 шт. ( = 100), а среднеквадратическое
отклонение - 10 шт. ( = 10). Если в начале месяца в запасе имеется 110
ед., сколько изделий нам может не хватить?
Для ответа на этот вопрос придется вычислить сумму произведений:
E(z) = 1∙P( =111) + 2∙P( =112) + 3∙P( =113) + ...,
где P( =111) - вероятность того, что потребуется 111 шт., т.е. не
хватит одного изделия;
P( =112) - вероятность того, что потребуется 112 шт., т.е. не
хватит двух изделий;
P( =113) - вероятность того, что потребуется 113 шт., т.е. не
хватит трех изделий и т.д.
Такое суммирование даст нам количество изделий, которых может
не хватить, если запас в начале месяца составляет 110 шт.
Решение такой задачи - дотаточно трудоемкий процесс. Однако в
настоящее время значения E(z) табулированы. Соответствующая
статистическая таблица (так называемая таблица Брауна) показывает
зависимость ожидаемого дефицита изделий (E(z)) от резервного запаса,
выраженного в стандартных отклонениях спроса (z). При этом табличные
значения приведены к стандартному отклонению спроса, равному
единице.
Далее
продолжим
рассмотрение
обсуждаемого
подхода
применительно к каждой из двух основных стратегий управления
запасами.
7.1 Модель с фиксированным размером заказа и уровень
обслуживания
При использовании такой стратегии уровень запаса отслеживается
непрерывно. Опасность исчерпания запаса возникает здесь только в
течение времени выполнения заказа (в течение заготовительного
периода).
В течение периода (см. рисунок 4.14) возможны колебания спроса.
Этот диапазон вычисляется либо на основе анализа ретроспективных
данных, либо на основе некоторой предположительной оценки (если
данные за прошедшие периоды невозможно получить).
Величина резервного запаса зависит от требуемого уровня
обслуживания. Объем партии заказа q вычисляется обычным способом.
Затем устанавливается "точка заказа", которая учитывает ожидаемую
потребность в течение заготовительного периода, плюс резервный
запас, определяемый требуемым уровнем обслуживания.
Рисунок 4.14 – Диапазон отклонений потребности в модели с фиксированным
размером заказа
Таким образом, важнейшее различие между моделью, в которой
потребность известна, и моделью, где потребность является случайной
величиной, заключается в определении "точки очередного заказа".
Объем заказа в обоих случаях одинаков. При этом элемент
неопределенности учитывается в резервном запасе.
"Точка заказа" вычисляется следующим образом:
S= ∙ +
(4.17)
где - средняя интенсивность спроса;
- средняя продолжительность заготовительного периода;
z - число стандартных отклонений спроса в резервном запасе
для заданного уровня обслуживания;
- стандартное отклонение спроса в течение заготовительного
периода.
В формуле (4.17) слагаемое ∙ определяет ожидаемый спрос в
течение заготовительного периода, а слагаемое
представляет собой
величину резервного запаса.
Остановимся на определении величин z и .
Значение
определяется в зависимости от условий задачи. Будем
рассматривать три случая.
1. Если изменяется только спрос, а продолжительность
заготовительного периода – величина постоянная, то:
(4.18)
где - стандартное отклонение спроса в единицу времени.
2. Если изменяется только заготовительный период, а спрос
остается постоянным, то:
(4.19)
где
стандартное
отклонение
продолжительности
заготовительного периода.
3. Наконец, если изменяются и спрос, и заготовительный период, то:
(4.20)
Перейдем к определению z. Для этого вычисляется E(z) - дефицит
изделий, который удовлетворяет заданному уровню обслуживания, а
затем по таблице Брауна находится соответствующее значение z.
Для вычисления E(z) используется формула:
(4.21)
где p - требуемый уровень обслуживания, в долях единицы;
соответственно, (1 - p) - неудовлетворенная часть потребности;
q - экономичный размер заказа (вычисляется обычным
образом);
E(z) – ожидаемый дефицит изделий в каждом цикле заказа,
выраженный в стандартных отклонениях спроса.
7.2 Модель с фиксированной периодичностью
уровень обслуживания
заказа
и
Модель с фиксированной периодичностью предполагает, что
размеры заказов различны для разных циклов. Таким образом, размер
запаса регулируется за счет изменения объема партии. Возобновление
же заказа определяется временем. Следовательно, модель с
фиксированной периодичностью должна иметь защиту от исчерпания
запасов (резервный запас) не только на время исполнения заказа, но и
на весь последующий цикла заказа (см. рисунок 4.15).
Таким образом, модель с фиксированной периодичностью больше
нуждается в резервном запасе, чем модель с фиксированным размером
партии.
Рисунок 4.15 – Вероятностная модель с фиксированной периодичностью заказа
Рассмотрим ситуацию с переменным спросом и постоянной
продолжительностью заготовительного периода. Ситуация наиболее
частая с точки зрения практики, а также наиболее простая для изучения.
Объем заказа в такой модели будет определяться по следующей
схеме:
Объем
заказа
Ожидаемый спрос в
течение цикла
=
заказа и
+
заготовительного
периода
Резервный
запас
Наличный запас
в момент
подачи заявки.
Соотношение, представленное на схеме, запишем в виде формулы:
q = (l + ) +
- Z,
(4.22)
где q - размер очередного заказа;
- средняя интенсивность спроса;
l - промежуток времени между подачей заявок;
- продолжительность заготовительного периода;
z - число стандартных отклонений спроса в резервном запасе
для заданного уровня обслуживания;
- стандартное отклонение спроса в течение цикла заказа и
заготовительного периода;
Z – текущий уровень запаса.