й уровень 1- ABCDA . Выберите
реклама
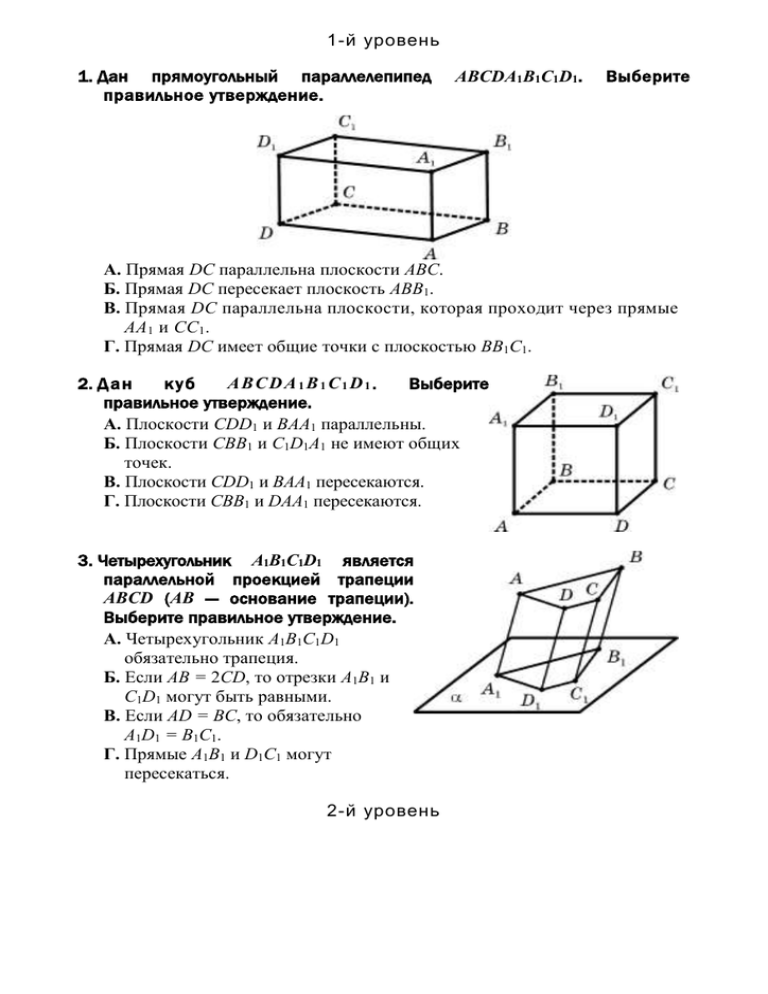
1-й уровень 1. Дан прямоугольный параллелепипед правильное утверждение. ABCDA1B1C1D1. Выберите А. Прямая DC параллельна плоскости ABC. Б. Прямая DC пересекает плоскость ABB1. В. Прямая DC параллельна плоскости, которая проходит через прямые AA1 и CC1. Г. Прямая DC имеет общие точки с плоскостью BB1C1. 2. Д ан к уб AB C D A 1 B 1 C 1 D 1 . Выберите правильное утверждение. А. Плоскости CDD1 и BAA1 параллельны. Б. Плоскости CBB1 и C1D1A1 не имеют общих точек. В. Плоскости CDD1 и BAA1 пересекаются. Г. Плоскости CBB1 и DAA1 пересекаются. 3. Четырехугольник A1B1C1D1 является параллельной проекцией трапеции ABCD (AB — основание трапеции). Выберите правильное утверждение. А. Четырехугольник A1B1C1D1 обязательно трапеция. Б. Если AB = 2CD, то отрезки A1B1 и C1D1 могут быть равными. В. Если AD = BС, то обязательно A1D1 = B1С1. Г. Прямые A1B1 и D1C1 могут пересекаться. 2-й уровень 4. Параллелограмм ы A B C D и ABKL лежат в разных плоскостях. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. А. Плоскость ABC и прямая KL параллельны. Б. Плоскость ABC пересекается с прямой KL. В. Прямая DC параллельна плоскости ABK. Г. Прямая AC параллельна плоскости BKL. 5. Две параллельные плоскости и пересекаются плоскостью по прямым a и b. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. А. Любая прямая, которая лежит в плоскости , обязательно пересекает обе плоскости и . Б. Прямые a и b могут быть скрещивающимися. В. Прямые a и b обязательно параллельны. Г. Прямая a параллельна плоскости . 6. Четырехугольник A1B1C1D1 является параллельной проекцией квадрата ABCD на некоторую плоскость. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. А. В четырехугольнике A1B1C1D1 может не быть параллельных сторон. Б. Диагонали четырехугольника A1B1C1D1 точкой пересечения делятся пополам. В. В четырехугольнике A1B1C1D1 может не быть равных сторон. Г. Четырехугольник A1B1C1D1 является трапецией. 3-й уровень 7. Плоскость пересекает стороны BA и BC треугольника ABC в точках K и L, причем AB : KB = BC : BL. Отметьте, какие из следующих че тыре х утве ржд ен ий правиль н ые , а какие — неправильные. А. Если AB : KB = 2, AC = 20 см, то KL = 10 см. Б. Прямая KL параллельна прямой AC. В. Угол BAC больше угла BKL. Г. Прямая AC параллельна плоскости . 8. Даны две различные плоскости и . Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. А. Если через точку M, которая не принадлежит плоскостям и , можно провести две разные прямые, параллельные плоскостям и , то плоскости и обязательно пересекаются. Б. Если любая плоскость пересекает плоскости и по параллельным прямым, то плоскости и обязательно параллельны. В. Если любая плоскость , которая пересекает плоскость , пересекает также плоскость , то плоскости и обязательно параллельны. Г. Если каждая прямая плоскости не лежит в плоскости , то плоскости и параллельны. 9. Прямые a1 и b1 являются параллельными проекциями прямых a и b на некоторую плоскость. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. А. Если прямые a1 и b1 пересекаются, то прямые a и b могут быть скрещивающимися. Б. Если прямые a и b пересекаются, то прямые a1 и b1 пересекаются. В. Если прямые a и b скрещивающиеся, то прямые a1 и b1 обязательно параллельны. Г. Если прямые a и b лежат в одной плоскости, то прямые a1 и b1 могут пересекаться. 4-й уровень 10. Прямые a и b скрещивающиеся. На прямой a заданы точки A1, A2, A3, а на прямой b — точки B1, B2, B3. Точки M, N, K являются соответственно серединами отрезков A1B1, A2B2 и A3B3. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. А. Прямая a не пересекает плоскость MNK. Б. Прямая b обязательно параллельна плоскости MNK. В. Если A1A2 = 2 см, а B1B2 = 3 см, то MN может равняться см. Г. Середина любого отрезка с концами на прямых a и b обязательно принадлежит плоскости MNK. 11. Три параллельные плоскости , , пересекают две данные скрещивающиеся прямые a и b в точках A1, A2, A3 и B1, B2, B3 соответственно (точка A2 лежит между точками A1 и A3, точка B2 лежит между точками B1 и B3). Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. А. Если A2A3 = 2 см, B1B2 = 8 см, A1A2 = B2B3, то B1B3 = 10 см. Б. Прямые B1A3 и B2B3 пересекаются. В. Прямые A1B1 и A3B3 могут быть параллельными. Г. A1A3 : B1B3 = A2A3 : B2B3. 12. Точка O — точка пересечения медиан треугольника ABC, — плоскость, которая не пересекает треугольник ABC. Через точки A, B, C, O проведены параллельные прямые, которые пересекают плоскость соответственно в точках A1, B1, C1, O1. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. А. 3OO1 = AA1 + CC1 + BB1. Б. Треугольник ABC обязательно подобен треугольнику A1B1C1. В. Четырехугольник A1ABB1 обязательно является параллелограммом. Г. Медианы треугольника A1B1C1 обязательно пересекаются в точке O1.

