Расчет переход. процес. в лин. электр. цепях

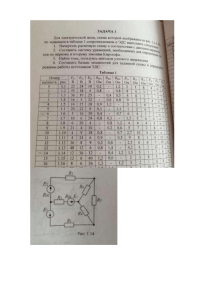
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
КАМЫШИНСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ (ФИЛИАЛ)
ГОУ ВПО «ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
КАФЕДРА «ЭЛЕКТРОСНАБЖЕНИЕ ПРОМЫШЛЕННЫХ ПРЕДПРИЯТИЙ»
РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ
В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Методические указания к выполнению курсовой работы
по дисциплине: «Теоретические основы электротехники»
Волгоград
2011
УДК 621.3.049 (07)
Р 24
РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ:
методические указания к выполнению курсовой работы по дисциплине
«Теоретические основы электротехники» / Сост. А. Г. Сошинов, Т. В.
Копейкина; Волгоград. гос. техн. ун-т. – Волгоград, 2011. – 42 с.
Содержатся теоретические положения по расчету переходных процессов в линейных электрических цепях классическим и операторным
методами, приводятся типовые задачи на расчет переходных процессов.
Предназначены для студентов направления 140200 «Электроэнергетика», специальности 140211 «Электроснабжение».
Ил. 18. Табл. 6. Библ.: 5 назв.
Рецензент: к. п. н., доцент Н. Г. Юдин
Печатается по решению редакционно-издательского совета
Волгоградского государственного технического университета

2
Волгоградский
государственный
технический
университет, 2011
Содержание
1.
2.
3.
Введение……………………………………………………………...
Теоретические положения…………………………………………..
1.1 Расчет переходных процессов в линейных электрических
цепях классическим методом………………………………...
1.2 Расчет переходных процессов в линейных электрических
цепях операторным методом…………………………………
Примеры решения задач…………………………………………….
2.1 Расчет переходных процессов в линейных электрических
цепях классическим методом………………………………...
2.2 Расчет переходных процессов в линейных электрических
цепях операторным методом…………………………………
Задание………………………………………………………….........
Список рекомендуемой литературы………………………………..
3
4
5
5
20
30
30
34
38
41
Введение
Настоящие методические указания предназначены для студентов очной формы, обучающихся по направлению 140200.62 «Электроэнергетика» и специальности 140211.65 «Электроснабжение» и выполняющих
курсовую работу по дисциплине «Теоретические основы электротехники» на тему «Расчет переходных процессов в линейных электрических
цепях». В результате выполнения данной курсовой работы студент знакомится с природой переходных процессов и основными методами анализа переходных процессов в линейных электрических цепях. В данных
методических указаниях более подробно рассматривается расчет переходных процессов в линейных электрических цепях классическим и операторным методами как с помощью приведенных теоретических положений, так и с помощью конкретных примеров решения задач.
Методические указания содержат задание на курсовую работу,
включающее в себя расчет классическим и операторным методами линейной разветвленной электрической цепи, содержащей в общем виде
сопротивление и индуктивность, а также расчет линейной разветвленной
электрической цепи, содержащей в общем виде сопротивление, индуктивность и емкость.
В результате изучения данного материала студенты получат полное
представление об анализе переходных процессов в линейных электрических цепях классическим и операторным методами, а также приобретут
навыки расчета неразветвленных и разветвленных электрических цепей.
Требования, предъявляемые к оформлению курсовой работы:
1. Курсовая работа выполняется на листах формата А4. На титульном листе должны быть указаны: дисциплина, тема курсовой работы,
группа, фамилия и инициалы студента, выполнившего курсовую работу,
а также фамилия и инициалы преподавателя, проверяющего курсовую
работу.
2. Текст задания, исходные данные и электрическая схема оформляются на отдельном листе.
3. Решение начинается со следующего листа и записывается только
на одной стороне каждого листа. Все листы должны быть пронумерованы.
4. Все основные решения должны иметь подробные пояснения, иллюстрироваться схемами, чертежами, векторными диаграммами и т.д.
5. Графическая часть работы должна быть выполнена аккуратно с
соблюдением ГОСТа на основные графические обозначения. Графики
диаграммы выполняются с обязательным соблюдением масштаба.
6. Курсовая работа должна содержать выводы и использованную
литературу.
4
1.
Теоретические положения
При всех изменениях в электрической цепи: включении, выключении, коротком замыкании, колебаниях величины какого-либо параметра
и т.п. – в ней возникают переходные процессы, которые не могут протекать мгновенно, так как невозможно мгновенное изменение энергии, запасенной в электромагнитном поле цепи. Таким образом, переходный
процесс обусловлен несоответствием величины запасенной энергии в
магнитном поле катушки и электрическом поле конденсатора ее значению для нового состояния цепи.
При переходных процессах могут возникать большие перенапряжения, сверхтоки, электромагнитные колебания, которые могут нарушить
работу устройства вплоть до выхода его из строя. С другой стороны, переходные процессы находят полезное практическое применение, например, в различного рода электронных генераторах. Все это обусловливает
необходимость изучения методов анализа нестационарных режимов работы цепи.
Основные методы анализа переходных процессов в линейных цепях:
 Классический метод, заключающийся в непосредственном интегрировании дифференциальных уравнений, описывающих электромагнитное состояние цепи.
 Операторный метод, заключающийся в решении системы алгебраических уравнений относительно изображений искомых переменных с
последующим переходом от найденных изображений к оригиналам.
 Частотный метод, основанный на преобразовании Фурье и находящий широкое применение при решении задач синтеза.
 Метод расчета с помощью интеграла Дюамеля, используемый
при сложной форме кривой возмущающего воздействия.
 Метод переменных состояния, представляющий собой упорядоченный способ определения электромагнитного состояния цепи на основе решения системы дифференциальных уравнений первого прядка, записанных в нормальной форме (форме Коши).
1.1 Расчет переходных процессов в линейных электрических
цепях классическим методом
Классический метод расчета переходных процессов заключается в
непосредственном интегрировании дифференциальных уравнений, описывающих изменения токов и напряжений на участках цепи в переходном процессе.
В общем случае при использовании классического метода расчета
составляются уравнения электромагнитного состояния цепи по законам
5
Ома и Кирхгофа для мгновенных значений напряжений и токов, связанных между собой на отдельных элементах цепи соотношениями, приведенными в табл. 1.1.
Таблица 1.1
Законы коммутации
Название закона
Первый закон
коммутации (закон сохранения
потокосцепления)
Второй закон
коммутации (закон сохранения
заряда)
Формулировка закона
В любой цепи с катушкой индуктивности, сцепленный с ней магнитный поток и проходящий по ней ток не могут изменится скачком. В момент коммутации и после нее ток и магнитный поток равен току и магнитному потоку, которые были в предшествующем
режиме, т.е. перед коммутацией.
В любой цепи с конденсатором заряд и напряжение на емкости не
могут изменится скачком. В момент коммутации заряд и напряжение равно заряду и напряжению, которые были в предшествующем режиме, т.е. перед коммутацией.
Более общей формулировкой законов коммутации является положение о невозможности скачкообразного изменения в момент коммутации
для схем с катушкой индуктивности – потокосцеплений, а для схем с
конденсаторами – зарядов на них. В качестве иллюстрации сказанному
могут служить схемы, представленные на рис. 1.1 а, б. Переходные процессы, возникающие в них, относятся к так называемым некорректным
коммутациям (название произошло от пренебрежения в подобных схемах
малыми параметрами, корректный учет которых может привести к существенному усложнению задачи).
а)
б)
Рис. 1.1 Электрические схемы:
а) с конденсаторами; б) с катушками индуктивности
Так, при переводе ключа из положения 1 в положение 2 (рис. 1.1, а),
трактование
второго
закона
коммутации как
невозможность скачкообразного напряжения в конденсаторе приводит к невыполнению второго закона Кирхгофа: иС1 0   иС 2 0  .
Аналогично при размыкании ключа в схеме на рис. 1.1,б трактование
первого закона коммутации как невозможность скачкообразного изменения тока через катушку индуктивности приводит к невыполнению перво6
го закона Кирхгофа i1 0   i2 0  . Для данных схем, исходя из сохранения
заряда и соответственно потокосцепления, можно записать:
C1иС1 0    C2иС 2 0    C1U 0  C1  C2 иС 0  ;
L1i1 0   Mi2 0   L2i2 0   Mi1 0   L1  L2  2M i 0  .
При анализе переходных процессов необходимо знать начальные
условия, т.е. значения токов и напряжений на отдельных участках цепи в
момент коммутации. Они могут быть зависимыми и независимыми. Независимыми начальными условиями называются значения токов в индуктивностях и напряжений на емкостях, которые были непосредственно перед коммутацией, и которые не изменили своих величин как в момент
коммутации так и сразу после нее. Зависимыми начальными условиями
называются значения остальных токов и напряжений, а также производных от искомой функции в момент коммутации, определяемые по независимым начальным условиям при помощи уравнений, составляемых по
законам Кирхгофа для t  0 .
1.1.1 Общие принципы анализа переходных процессов
Расчет переходных процессов в линейных электрических цепях
классическим методом сводится к составлению и решению системы
уравнений, записанных на основе законов Кирхгофа для мгновенных
значений электрических величин применительно к послекоммутационной
схеме.
Уравнения, составленные на основании первого закона Кирхгофа
для каждого независимого узла, имеют вид:
iк  0 ,
уравнения, составленные на основании второго закона Кирхгофа для
каждого независимого контура, имеют вид:

di
q 
 eк    rк iк  Lк dtк  Cк 
к 

Таким образом, система уравнений, описывающая переходный процесс в сложной электрической цепи, состоит из (q—1) уравнений, составленных по первому закону Кирхгофа, и из (р—q+1) уравнений — по второму
закону
Кирхгофа.
Она
является
системой
интегродифференциальных уравнений с постоянными коэффициентами rк , Lк ,
Mк и Cк.
Совместное решение этих уравнений относительно какого-либо переходного тока (напряжения) приводит к дифференциальному уравне7
нию, n-ого порядка для искомой величины, которое в общем виде может
быть написано:
d ni
dt
n
 a1
d n1i
dt
n1
   an1
di
 ani  f t  ,
dt
(1)
где aк – постоянные коэффициенты, зависящие от параметров электрической цепи;
f (t) – известная функция времени, определяемая приложенными
напряжениями или э. д. с. источников.
Порядок этого уравнения равен числу независимых начальных условий для необъединяемых индуктивностей и емкостей эквивалентной послекоммутационной схемы. Так, например, для определения порядка
уравнения, описывающего переходный процесс в электрической цепи
(рис. 1.2), производим замену данной цепи эквивалентной схемой (рис.
1.3).
Рис. 1.2 Электрическая схема
В данной схеме индуктивности неразветвленного участка объединяются в эквивалентную индуктивность L1 = Ll' + L1"±2M (в зависимости от
способа включения катушек), а эквивалентная емкость участка равна:
C 'C ' '
C34  C3  '' 4 4 '' .
C4  C4
В эквивалентной схеме имеется две необъединяемых индуктивности
и одна емкость, т. е. число независимых начальных условий равно трем.
Поэтому порядок дифференциального уравнения, описывающего переходный процесс в цепи (рис. 1.2), также равен трем.
Решение неоднородного линейного дифференциального уравнения
(1) сводится к нахождению общего интеграла его, который определяет
закон изменения рассматриваемого тока (напряжения) во времени в течение переходного процесса.
8
Как известно из математики, общий интеграл неоднородного линейного дифференциального уравнения может быть представлен в виде суммы, состоящей из частного решения неоднородного дифференциального уравнения и общего решения такого же дифференциального
уравнения без свободного члена, т. е. однородного уравнения.
Рис. 1.3 Электрическая схема
Частное решение неоднородного линейного дифференциального
уравнения выражает принужденный режим работы цепи inp (t) имеющий
место после окончания переходного процесса, т. е. для момента времени
t=∞. Принужденный режим определяется характером эдс (напряжения)
источника питания и параметрами послекоммутационной схемы.
Если в послекоммутационной схеме действуют постоянные или гармонические эдс, то принужденный режим одновременно будет и установившимся. Установившиеся процессы рассчитываются методами, принятыми для расчета цепей постоянного или переменного токов.
Общее решение однородного линейного дифференциального уравнения выражает свободный режим работы цепи iсв(t) при переходном
процессе. Свободный ток iсв определяется из уравнения:
d ni
d n 1i
di
 a1  n 1     a n 1
 an i  0 .
n
dt
dt
dt
Для решения этого уравнения составляем характеристическое уравнение и находим его корни:
p n  a1 p n1    a n 1 p  a n  0 .
Если характеристическое уравнение не содержит сопряженных комплексных корней, то общее решение имеет вид:
(2)
iсв  A1e p t  A2 e p t    An e p t ,
1
2
n
где А1, А2,….., Аn – постоянные интегрирования;
p1, p2……, рп – корни характеристического уравнения;
е – основание натурального логарифма.
9
При наличии сопряженных комплексных корней, например, р12=-а±
jω, в общем решении удобнее соответствующую пару экспонент заменить функцией
(3)
Ae  at sin t    ,
где А и θ – постоянные интегрирования, заменившие постоянные А1,и А2;
α – коэффициент затухания.
Общее решение однородного линейного дифференциального уравнения описывает поведение цепи в продолжение переходного процесса
при отсутствии в цепи внешних источников энергии. Возникающий при
этом свободный режим является следствием наличия запаса энергии в
электрических и магнитных полях отдельных элементов. Причем количество запасенной энергии определяется начальными условиями.
Так как все реальные электрические цепи обладают сопротивлениями, на которых происходит рассеяние энергии, то свободный режим всегда является затухающим и продолжается он до тех пор, пока весь запас
энергии не будет полностью израсходован. После этого в цепи наступает
принужденный режим.
Поскольку скорость затухания свободного, режима зависит от интенсивности рассеяния энергии на сопротивлениях, то изменением параметров цепи можно регулировать как продолжительность свободного, так
и переходного процессов.
Так как закон изменения свободной составляющей зависит от параметров электрической цепи, то при наличии в цепи помимо сопротивлений или одних индуктивностей или одних емкостей свободные составляющие токов или напряжений всегда затухают по показательному закону. Если же в цепи имеются, и индуктивности и емкости, то при определенном соотношении параметров возможно появление затухающих колебаний, при которых энергия магнитного поля переходит в энергию электрического поля и наоборот.
Общий интеграл неоднородного линейного дифференциального
уравнения (1), определяющий действительный ток в цепи при переходном процессе, может быть записан:
(4)
i  iпр  iсв
Такое разложение действительных токов (напряжений) на принужденную и свободную составляющие является расчетным приемом, облегчающим анализ переходных процессов. В реальных цепях имеют место
только одни действительные токи (напряжения).
В состав общего интеграла (4) входят постоянные интегрирования А1
А2,…,Ап, число которых равно порядку дифференциального уравнения.
Для определения постоянных интегрирования производится расчет
предшествующего режима работы цепи и определяются все токи в ин10
дуктивностях и напряжения на емкостях, которые имеют место непосредственно перед коммутацией, т.е. iL,(0) и uс,(0).При числе постоянных
больше одной, что имеет место при дифференциальных уравнениях второго и больших порядков помимо начальных значений iL (0) и ис (0)
необходимо определить еще величины производных от токов и напряжений также в момент коммутации, т. е.:
di
dt
t 0 ;
d 2t
dt 2
;
t 0
d n 1i
dt n 1
t 0
Затем производится расчет принужденного режима послекоммутационной схемы, для которого определяются значения токов индуктивностях и напряжений на емкостях, а также их производных во времени в
момент коммутации, т. е.:
iпр 0 ;
diпр
dt
t  0
n 1
d пр
i

dt n 1
t 0
Затем составляется система n-уравнений, позволяющая определить
как начальные значения свободных токов (напряжении) и их производных, так и все постоянные интегрирования.
i 0   iпр 0   iсв 0   A1  A2   An
di
dt
t 0 
diпр
dt

t 0
diсв
dt
t 0
 p1 A1  p2 A2    pn An


d n1iпр
d n1iсв
d n1i


 p1n1 A1  p2n1 A2    pnn1 An


n1 t 0
n1
dt
dt
dt
t 0
t 0
Подставляя в эту систему уравнений значения предшествующих
(начальные условия) и принужденных токов (напряжений), а так же их
производных в начальный момент времени и значения корней характеристического уравнения, находим все постоянные интегрирования А1, A2…,
Ап.
После этого постоянные интегрирования подставляются в уравнение
(4) и определяются законы изменения действительных токов в электрических цепях при переходных процессах.
Основной трудностью классического метода расчета переходных
процессов в линейных электрических цепях является определение постоянных интегрирования по заданным начальным условиям.
11
1.1.2 Переходные процессы в неразветвленных электрических
цепях с сопротивлением и индуктивностью
Общий анализ переходного процесса в цепи r, L
Будем полагать, что цепь, состоящая из последовательно соединенных сопротивлений r и индуктивности L (рис. 1.4), подключается к
источнику с эдс e(t).
Рис. 1.4. Электрическая схема
Переходный процесс в цепи после подключения ее к источнику описывается неоднородным линейным дифференциальным уравнением первого порядка:
di
(5)
ri  L  et  ,
dt
где e(t) - эдс источника, в общем случае являющаяся некоторой
функцией времени;
i – мгновенное значение тока в цепи.
Согласно (4), общее решение этого уравнения может быть записано:
(6)
i  i пр  icв
Принужденный ток inp зависит от вида приложенной эдс и параметров цепи iпр =F[e(t), r , L]. Поэтому определение его будет выполнено
ниже, при рассмотрении конкретных режимов работы цепи.
Свободный ток iсв определяется общим решением однородного линейного дифференциального уравнения:
di
riсв  L св  0 .
dt
Соответствующее ему характеристическое уравнение имеет вид:
r + pL = 0,
а корень характеристического уравнения равен:
12
r .
L
Линейное дифференциальное уравнение первого порядка всегда
имеет только один отрицательный действительный корень.
Общее решение однородного дифференциального уравнения первого порядка (7) может быть записано:
p1  
r
 t
L
Ae
.
(7)
icв  Ae 
Уравнение свободного тока (7) графически изображается затухающей кривой—экспонентой (рис. 1.5), у которой при t = 0 ордината равна
постоянной интегрирования А.
Уменьшение свободного, тока в цепи происходит тем быстрей, чем
больше отношение сопротивления к индуктивности. Это отношение r/L
=  называется коэффициентом затухания. Коэффициент затухания численно равен корню характеристического уравнения.
Величина, обратная коэффициенту затухания   1  L , называется
 r
постоянной времени цепи. Свое наименование она получила потому, что
единицей измерения ее является единица времени – секунда:
 L  гн ом  сек
.
 r   ом  ом  сек
Постоянная времени является таким временем, по прошествии которого, начиная с произвольного момента времени t, свободный ток
уменьшится в е раз по сравнению с первоначальным значением его. Действительно, свободный ток в момент времени t+τ равен:
p1t
r
 t
Ae L iсв t 
iсв t     Ae


e
e
т. е. он в е раз меньше своего первоначального значения.
Если отсчет времени качать в момент t = 0, то:

r
t  
L
iсв   
A icв 0

e
e
13
Рис. 1.5. График зависимости тока от времени
i
Так как: diсв   iсв или    св , то графически постоянная
dt

diсв / dt
времени цепи τ определяется длиной подкасательной в любой точке кривой свободного тока. Если за начало отсчета времени принято t = 0, то
постоянная времени изображается длиной подкасательной ОВ (рис. 1.5),
которая равна:
i 0
i 0
OB  OCctg  св   св

tg
diсв / dt
Значения свободного тока в цепи, выраженные в процентах от его
начального значения icв(0), могут быть определены для различных моментов времени t, которые обычно берутся кратными постоянной времени цепи τ. Результаты такого расчета сведены в табл. 1.2.
Таблица 1.2
Результаты расчета
t
0
τ
2τ
3τ
4τ
5τ
6τ
∞
iсв t 
100 %
iсв 0
100
36,8
13,5
5
1,8
0,67
0,25
0
Отсюда следует, что за время t= (3÷5)τ свободный ток в цепи почти
полностью затухает. Следовательно, в большинстве инженерных расче-
14
тов можно считать, что за время (3÷5)τ переходный процесс практически
заканчивается.
Так как продолжительность переходного процесса определяется постоянной времени, которая в свою очередь зависит от параметров цепи,
то посредством изменения параметров можно регулировать продолжительность переходного процесса.
Из всего оказанного очевидно, что цепи с сопротивлением r и индуктивностью L являются инерционными цепями. Инерционность цепи состоит в том, что при любом мгновенном изменении параметров цепи или
приложенного напряжения ток в цепи изменяется постепенно, т. е. в своем изменении он отстает от напряжения.
Включение цепи с сопротивлением и индуктивностью
под постоянное напряжение
Рассмотрим переходный процесс, возникающий при включении катушки с сопротивлением R и индуктивностью L под постоянное напряжение U.
Очевидно, что в предшествующем режиме ток в катушке отсутствовал, а по прошествии бесконечно большего времени, когда переходный процесс закончится, принужденный ток составит:
U
i пр   I .
R
Переходный процесс в послекоммутационной схеме описывается
уравнением:
di
Ri  L  U ,
dt
общее решение которого:
i  iпр  icв  iпр  Ае R / L t .
Подставив сюда принужденное значение тока, получим:
i  I  Ae R / L t .
Постоянная интегрирования определяется из начального условия:
i(0)  0  I  A или A   I .
Окончательно закон изменения тока в катушке примет
вид:
U
(1  e ( R / L) / t ).
R
График изменения его в продолжение переходного процесса приведен на рис. 1.6.
i  I (1  e ( R / L)t ) 
15
Рис. 1.6. Скорость нарастания тока в катушке
Из уравнения и графика изменения тока в катушке следует, что в
момент включения свободный ток в катушке iсв(0)=-I равен по величине и
противоположен по знаку принужденному току iпр(0)=I. Поэтому действительный ток в катушке отсутствует (i(0)=0). По окончании переходного процесса свободный ток уменьшается до нуля и действительный ток
становится равным принужденному.
Значения тока в катушке, выраженные в процентах от принужденного, для различных моментов времени приведены в табл. 1.3.
Таблица 1.3
Результаты расчетов
t
[i (t )/I] 100 %
0
1
2
3
4
5
6
0
63,2
86,5
95
98,2
99,3
100
Скорость нарастания тока в катушке определяется величиной постоянной времени цепи  =L/R, которая равна длине подкасательной,
построенной для любой точки кривой тока i(t). Для точки t=0 постоян16
ная времени  изображается отрезком ВС. В результате изменения
тока в катушке наводится эдс самоиндукции.
В момент включения ЭДС самоиндукции равна и противоположно
направлена приложенному напряжению e L (0)=-U.
eL  L
di
d
  L ( I  Ie ( R / L)t )   RIe ( R / L)t  Ue ( R / L)t .
dt
dt
(8)
Последнее как раз и объясняет отсутствие тока в катушке в момент
включения. В последующем по мере уменьшения ЭДС самоиндукции в
соответствии с уравнением (8) увеличивается разность между напряжением источника U и ЭДС самоиндукции eL. Это сопровождается увеличением тока в цепи.
Напряжение на сопротивлении цепи:
и  Ri  RI 1  e  R / L t  U 1  e  R / L t ,
а

 

в момент включения катушки напряжение равное нулю иа(0) =0, постепенно увеличивается и по окончании переходного процесса достигает
величины напряжения источника ипр = U.
На практике рассмотренный переходный процесс имеет место при
включении двигателей постоянного тока, в соленоидах приводов масляных выключателей, при измерении сопротивлений постоянному току обмоток электрических машин и трансформаторов.
1.1.3 Переходные процессы в неразветвленных электрических
цепях с сопротивлением и емкостью
Общий анализ переходного процесса в цепи r, С
Будем полагать, что цепь, состоящая из последовательно соединенных сопротивления r и емкости С, подключается к источнику с эдс e(t),
Переходный процесс в цепи после подключения ее к источнику описывается уравнением:
(9)
ri  u c  et 
Это уравнение удобно записать относительно напряжения на
емкости uC , так как емкость дает независимое начальное условие. Имеем
в виду, что ток в цепи равен:
i
du
dq
C C
dt
dt
и подставив значение тока в уравнение (9), получим:
du
rC C  uC  et 
dt
17
(10)
где, e(t) — эдс источника, в общем случае являющаяся некоторой
функцией времени;
ис — действительное напряжение на емкости.
Последнее уравнение (10) является неоднородным линейным дифференциальным уравнением первого порядка. По своей структуре оно
аналогично уравнению (5), описывающему переходный процесс в цепи r,
L. Поэтому и характер протекания переходных; процессов в обеих цепях
одинаковый с той лишь разницей, что в цепи r, С определяется изменение
напряжения на емкости uс, а в цепи r, L - изменение тока i.
Общее решение уравнения (10) может быть записано:
uC  uC пр  uC св
Принужденное напряжение uСпр зависит от вида приложенной эдс
e(t) и параметров цепи. Поэтому определение его выполнено ниже при
рассмотрении конкретных режимов работы цепи.
Свободное напряжение uСсв определяется из решения однородного
линейного дифференциального уравнения:
du
(11)
rC C  uC  0
dt
Соответствующее ему характеристическое уравнение имеет вид:
rCp  1  0
,а корень характеристического уравнения равен:
p1  
1
rC
Общее решение однородного дифференциального уравнения (11)
может быть записано:

1
t
u Ссв  Ae p1t  Ae rC
Аналогично цепи r, L зависимость свободного напряжения на емкости uСсв от времени изображается экспонентой с начальным значением,
равным А, и коэффициентом затухания   1 . Постоянная времени цеrС
пи r, С равна τ=rC. Постоянная времени цепи также измеряется в секундах.
rС   ом    ом  а  сек  сек .
в
Таким образом, общее решение уравнения может быть записано:
u C  u Cпр  Ae p1t  u Cпр  Ae

t
rC
Отсюда нетрудно определить и закон изменения тока в послекоммутационной схеме во время переходного процесса:
18
t
duпр
du
du
A 
iC C C
 C Ccв  iпр  e rC
dt
dt
dt
r
(12)
Включение под постоянное напряжение цепи с сопротивлением и предварительно заряженным конденсатором
Предположим, что под постоянное напряжение U включается цепь с
сопротивлением R и конденсатором с емкостью С, который предварительно заряжен до напряжения Uo. Это напряжение направлено навстречу
внешнему, а по величине оно меньше, чем напряжение источника
(U0<U).
В предшествующем режиме имеет место ненулевое начальное условие ис (0) = Uo, а принужденное напряжение на емкости после окончания
переходного процесса равно напряжению источника (uCnp = U).
Переходный процесс в послекоммутационной схеме описывается уравнением:
du
RC c  u c  U
dt
Общее решение его равно:
uC  uСпр  Ае (t / RC) .
Постоянная интегрирования определяется из начального условия:
uC  uСпр  uCcв  U  Ае (t / RC) .
uC (0)  U 0  U  А или A  U 0  U
Окончательно закон изменения напряжения на емкости:
u C  U  (U 0  U )e  (t / RC ) .
Ток в послекоммутационной схеме:
du
U  U 0 (t / RC)
i C C 
e
.
dt
R
Графики изменения uc(i) и i(t) приведены на рис. 1.7:
19
Рис. 1.7. График изменения напряжения на конденсаторе и зарядного тока во времени
1.2 Расчет переходных процессов в линейных электрических
цепях операторным методом
Сущность операторного метода заключается в том, что функции
f t  вещественной переменной t, которую называют оригиналом, ставится в соответствие функция F  p  комплексной переменной
p  s  j , которую называют изображением. В результате этого производные и интегралы от оригиналов заменяются алгебраическими функциями от соответствующих изображений (дифференцирование заменяется умножением на оператор р, а интегрирование – делением на него), что
в свою очередь определяет переход от системы интегродифференциальных уравнений к системе алгебраических уравнений относительно изображений искомых переменных. При решении этих уравнений находятся изображения и далее путем обратного перехода – оригиналы. Важнейшим моментом при этом в практическом плане является
необходимость определения только независимых начальных условий, что
существенно облегчает расчет переходных процессов в цепях высокого
порядка по сравнению с классическим методом.
1.2.1 Прямое и обратное преобразование Лапласа
Изображение F  p  заданной функции f t  определяется в соответствии с прямым преобразованием Лапласа:
_ 
F  p    e  pt f t dt
13)
  0
В сокращенной записи соответствие между изображением и оригиналом обозначается, как:
20
(
_
f t 
F  p 
 
Функция вещественного переменного оригинал определяется при
помощи обратного преобразования Лапласа:
_
f t   L1 F  p 
 
Следует отметить, что если оригинал f t  увеличивается с ростом
t, то для сходимости интеграла (13) необходимо более быстрое убывание
модуля e pt . Функции, с которыми встречаются на практике при расчете
переходных процессов, этому условию удовлетворяют.
В качестве примера в табл. 1.4 приведены изображения некоторых
характерных функций, часто встречающихся при анализе нестационарных режимов.
Таблица 1.4
Изображения типовых функций
А
sin t
cos t
Оригинал f t 
et
Изображение
_
F  p 
 
A
p
1
p 

p2   2
p
p2   2
Некоторые свойства изображений:
1. Изображение суммы функций равно сумме изображений слагаемых:
n
n
_
 f k t   Fk  p 
k 1  
k 1
2. При умножении оригинала на коэффициент на тот же коэффициент умножается изображение:
_
Af t 
AF  p 
 
С использованием этих свойств и данных табл. 1.4, можно показать,
например, что:

U 0 1  e t
21

U0
U0

p p 
f t 
В курсе математики доказывается, что если
_
F  p  , то
 
_
pF  p   f 0 , где f 0  - начальное значение функции f t  .
 
Таким образом, для напряжения на индуктивном элементе можно
записать:
_
di
LpI  p   Li 0
и L t   L
dt
 
df / dt
или при нулевых начальных условиях:
_
LpI  p 
 
Отсюда операторное сопротивление катушки индуктивности: Z  p   Lp
иL t   L
di
dt
_
F  p  , то
 
_
F  p 
t
 .
 f t dt
p
0
С учетом ненулевых начальных условий для напряжения на конден1t
саторе можно записать: иС t    idt иС 0
C0
Аналогично для интеграла: если f t 
Тогда:
иС t 
_
I  p 
   иС 0 
Cp
p
или при нулевых начальных условиях: иС t 
1 _,
I p
Cp  
откуда операторное сопротивление конденсатора: Z  p   1
  Cp
_
 
1.2.2 Законы Ома и Кирхгофа в операторной форме
Закон Ома в операторной форме:
22
Выделим ветвь m-n (рис. 1.8) из некоторой сложной цепи. Замыкание ключа во внешней цепи приводит к переходному процессу, при этом
начальные условия для тока в ветви и напряжения на конденсаторе в общем случае ненулевые.
Рис. 1.8. Электрическая цепь
Для мгновенных значений переменных можно записать:
иmnt   iR  L
di 1 t
  idt  иC 0  et 
dt C 0
Тогда на основании приведенных выше соотношений получим:
 _   _ 
_
и 0
1 
  Li 0  C  E  p 
U m n p   I  p  R  Lp 
Cp 
p
   
 
Отсюда:
_
_
и 0 
U m n p   Li 0   C
 E  p 
p
_
 
 ,
I  p  
_

 
Z  p 
 
(14)
где:
_
1
Z  p   R  Lp 
Cp
 
– операторное сопротивление рассматриваемого участка цепи.
23
Следует обратить внимание, что операторное сопротивление Z  p 
соответствует комплексному сопротивлению Z  j  ветви в цепи сину
соидального тока при замене оператора р на j .
Уравнение (14) есть математическая запись закона Ома для участка
цепи с источником ЭДС в операторной форме. В соответствии с ним для
ветви можно изобразить операторную схему замещения, представленную
на рис. 1.9.
Рис. 1.9. Операторная схема замещения
Законы Кирхгофа в операторной форме:
Первый закон Кирхгофа: алгебраическая сумма изображений токов, сходящихся в узле, равна нулю.
n
_
k 1
 
 I k  p   0 .
Второй закон Кирхгофа: алгебраическая сумма изображений ЭДС,
действующих в контуре, равна алгебраической сумме изображений
напряжений на пассивных элементах этого контура.
m
_ m
_
 Ek  p   U k  p  .
k 1
  k 1  
Рис. 1.10. Электрическая схема
24
При записи уравнений по второму закону Кирхгофа следует помнить
о необходимости учета ненулевых начальных условий (если они имеют
место). С их учетом последнее соотношение может быть переписано в
развернутом виде:
m
_
и 0  m 
1  _
  Ek  p   Lk ik 0  Ckp     R  Lp  Cp  I k  p  .
k 1
  
 
 k 1
В качестве примера запишем выражение для изображений токов в
цепи на рис. 1.9 для двух случаев: 1 – иС 0   0 ; 2 – иС 0   0 .
В первом случае в соответствии с законом Ома:
_
U 0  p 
_
U 0 1  R2Cp 
 
I1  p  

1

p
R
1R2Cp  R1  R2 
 
R2
Cp
R1 
1
R2 
Cp
Рис. 1.11. Электрическая схема
Тогда:
_
_
U0
1
I 2  p   I1 p 


R
Cp

1
p
R
R
Cp
 R1  R2 
1 2
 
  2
и
_
 _  R Cp
U 0 R2C
.
I 3  p   I1  p  2

 
  R2Cp  1 R1R2Cp  R1  R2
Во втором случае, т.е. при иС 0   0 , для цепи на рис. 1.10 следует
составить операторную схему замещения, которая приведена на рис. 1.11.
Изображения токов в ней могут быть определены любым методом расчета линейных цепей, например, методом контурных токов:
25
_
_
U
I11 p R1  R2   I 22 p R2  0 ;
p
 
_

иС 0 ,
1 
 I11 p  R2  I 22  R2 
   p
Cp


 
Откуда:
_
_
I1  p   I11 p  ,
 
 
_
_
_
I 2  p   I11 p   I 22  p  ,
 
 
 
_
_
I 3  p   I 22  p  .
 
 
1.2.3 Переход от изображений к оригиналам:
Переход от изображения искомой величины к оригиналу может быть
осуществлен следующими способами:
1. Посредством обратного преобразования Лапласа:
f t  
  j
1
pt
 F  p e dp ,
2j   j
которое представляет собой решение интегрального уравнения (13) и
сокращенно записывается, как: f t   L1F  p  .На практике этот способ
применяется редко.
2.По таблицам соответствия между оригиналами и изображениями:
Рис.1.12. Электрическая схема
26
В специальной литературе имеется достаточно большое число формул соответствия, охватывающих практически все задачи электротехники. Согласно данному способу необходимо получить изображение искомой величины в виде, соответствующем табличному, после чего выписать из таблицы выражение оригинала.
Например, для изображения тока в цепи на рис. 1.12 можно записать:
_


U 0  p 
U0
U0  1
1 .


 

I  p 


pR  pL R  p p  R 
_


Z  p 
L

 
Тогда в соответствии с данными табл. 1.3:
i t  
R
 t
U 0 
1 e L  ,

R 


что соответствует известному результату.
3. С использованием формулы разложения:
Пусть изображение F  p  искомой переменной определяется отношением двух полиномов:
_
F1  p 
_
b p m  bm 1 p m 1  ...b1 p  b0 ,
F  p      m n
n 1
_
  F  p  an p  an 1 p  ...a1 p  a0
2 
 
Где m <n.
Это выражение может быть представлено в виде суммы простых
дробей:
_
F1  p 
n
_
Ak
F  p      
_
  F  p  k 1 p  pk
2 
 
27
(15)
где рк- к-й корень уравнения F2  p   0 .
 
_
 
Для определения коэффициентов Ак умножим левую и правую части
соотношения (15) на (р- рк):
_
F1  p  p  pk 
n
.
 p  pk   Ak  Ak    _
 
i 1 p  pi
F2  p 
ik
 
_ 
При p  pk : A  F  p  lim  p  pk  .
k
1 k 
_
  p  pk F  p 
2 
 
Рассматривая полученную неопределенность типа 0/0 по правилу
Лапиталя, запишем:
d
 p  pk 
_ 
F p 
dp
Ak  F1 p k  lim
 1/ k .
_ 
p

p

F2  pk 
k
 
F2 /  p k 
 
Таким образом,
_
_ 
F1  p 
F1  p k 
n
 
  1 .
F  p 

_
  k 1 /  _  p  pk
F2  p 
F2  p k 
 
 
_ 
F1  p k 
  есть постоянный коэффициент, то учиПоскольку отношение
_ 
/
F2  p k 
 
t
1
тывая, что e
, окончательно получаем:
p 
28
_ 
F1  p k 
n
f t      e p k t
(16)
_ 
k 1 / 
F2  p k 
 
Соотношение (16) представляет собой формулу разложения. Если
_
_
_
один из корней уравнения F  p   0 равен нулю, т. е. F2  p   pF3  p  , то
2 
 
 
 
 
 
уравнение (16) сводится к виду:
_ 
F1  p k 
F 0
  e pk t .
f t   1  
F2 0 k 1
_ 
pk F2 /  p k 
 
n
В заключение необходимо отметить, что для нахождения
начального f 0  и конечного f   значений оригинала можно использовать предельные соотношения которые также могут служить для оценки
правильности полученного изображения:
_
f 0  lim pF  p  ;
p 
 
_
f    lim pF  p  .
p 0
 
29
2. Примеры решения задач
2.1 Примеры расчета переходных процессов в линейных электрических цепях классическим методом
Задача 1. Цепь (рис. 2.1, а) с R1 = 10 и R2 = 25 0м; L2 = 0,2 Гн; R3 = 50
Ом; L3 = 0,1 Гн с помощью рубильника S подключается к источнику с U =
= 200 В.
Определить законы изменения и построить графики токов в ветвях
цепи.
Решение:
Для определения токов в ветвях цепи составляем систему уравнений
Кирхгофа:
di

R1i1  R2i 2  L2 2  U
(17)

dt

di 
di
R2i2  L2 2  R3i 3  L3 3 
(18)
dt
dt 
i1  i2  i3

(19)


i,A
S
R1
6
+
i1
R2
R3
L2
L3
U
i2
i1
4
i2
i3
-
i3
2
t,c
0
0.0061
а)
а) электрическая схема,
0.0122
0.0183
б)
Рис. 2.1
б) графическая зависимость тока от времени
Эти системы решаем относительно тока i2. Из уравнения (19) определяем ток i3 = i1–i2 и подставляем его в (18):
30
di2
di
di
 R3i1  R3i2  L3 1  L3 2 .
dt
dt
dt
Решив уравнение (17) относительно тока i1:
L di
U R2
i1 

i2  2 2 ,
R1 R1
R1 dt
находим его производную:
R2i2  L2
(20)
(21)
di1
R di
L d 2 i2
(22)
 2 2  2
.
dt
R1 dt R1 dt 2
После подстановки уравнений (21) и (22) в (20) и дальнейшего преобразования получим:
d 2i2
dt
2
(
R1  R3 R1  R2 di2 R1R2  R2 R3  R3 R1
R

)

i2  3 U .
L3
L2
dt
L2 L3
L2 L3
(23)
или
d 2i2
di
(24)
 775 2  100000i 2  500000.
2
dt
dt
Общее решение этого уравнения:
i2 = i2пр + i2св.
Принужденный ток определяется как:
500000
i2пр=
 5А
100000
Свободный ток i2св определяется решением однородного уравнения:
d 2i2св
di
 775 2св  100000i2св  0.
2
dt
dt
Характеристическое уравнение:
р2 + 775р + 100 000 = 0,
корни р1,2 = – 387,5 ± 150156  100000 = – 387,5 ± 223,46.
Отсюда:
р1 = – 163,5 1/с; р2 = – 611,5 1/с.
Следовательно,
i2св = A1е-163,57t +A2e-611,5t
и действительный ток:
i2 = 5 + А1е-163,5t + A2e-611,5t.
31
(25)
Решив совместно уравнения (18) и( 1 9 ) относительно тока i3 и использовав уравнение:
di3
U,
dt
после преобразований, аналогичных рассмотренным, получим:
R1i1  R3i3  L3
d 2 i3
2
(
R1  R2 R1  R2 di3

)

L3
L2
dt
dt
R R  R2 R3  R3 R1
R
 1 2
i3  2 U ,
L2 L3
L2 L3
(26)
или
d 2i3
di
(27)
 775 3  100000i3  250000.
dt
dt
Действительный ток:
(28)
i3  2,5  B1e 163,5t  B2 e 611,5t .
В уравнения (28) и (25) входят четыре постоянных интегрирования
А1, А2, В1, В2. Для их определения используем два независимых начальных условия:
i 2 (0)=0=5 + A 1 + A 2 ;
(29)
i3 (0) = 0 = 2,5 + B1 + B2.
(30)
Дополнительные два начальных условия получаем исходя из того,
что i1 (0) =0. Поэтому в момент включения цепи к зажимам катушек будет приложено напряжение, равное напряжению источника. А уравновешено оно будет ЭДС самоиндукции, которые наводятся в катушках:
di
di
U  ( L2 2 )t  0  ( L3 3 )t  0
dt
dt
или
0,2(–163,5А 1 –611,5А 2 ) = –32,7А1– 122А2 = 200;
(31)
0,1 (–163,5В1 – 611,5В2) = – 16,35В1–61,15В2 = 200.
(32)
Решив совместно уравнения (29) и (31), найдем А1=4,59; А2 = –0,41, а
из совместного решения (30) и (32) определим В1=–3,55 и В2=1,05.
Подставив постоянные интегрирования в уравнения (25) и (28), получим токи в ветвях:
i2 = 5 – 4,59e-163,5t –0,41e-611,5tA;
i3 = 2,5 – 3,55е-163,5t + 1,05e-611,5t A
и ток в неразветвленной части цепи:
i1 = 7,5 – 8,14е-163,5t + 0,64e-611,5t А.
32
Графики
2.1,б.
изменения
токов в ветвях
цепи
показаны
на рис.
Задача 2. Цепь с R1 = 20 и R2 = 30 Ом; R3 = 10 Ом и С3 = 50пФ, с
помощью рубильника S подключается к источнику с U = 200 В
(рис. 2.2, а).
i,A
S
R1
+
7.5
i1
R3
i1
5
R2
U
C3
i2
i2
i3
2.5
-
i3
t,c
0
а)
а) электрическая схема,
2
б)
Рис. 2.2
б) графическая зависимость тока от времени
3
Определить законы изменения напряжения на конденсаторе и токов
в ветвях цепи.
Решение. Чтобы найти напряжение uC и токи в ветвях, составляем
систему уравнений Кирхгофа:
i1= i2 + i3
R1i1 + R2i2 = U
R2i2 = R3i3 + UC
Ток в третьей ветви:
i3 = C3 duC
dt
Выразив токи i1 и i2 через напряжение uC и его
лучим:
i2  C
 R  R3  duC uC
R3 duC uC

 .
 ; i1  C3  2
R2
R2 dt
R2
 R2  dt
Подставим их во второе уравнение системы:
33
производную, по-
duC
R1  R2
R2

uC 
U,
dt C3 ( R1R 2  R 2 R3  R1R 3 )
C3 ( R1R2  R2 R3  R1R3 )
или
duC 50  1012
30  1012

uC 
 200;
dt 50  1100
50  1100
duC
 9,09  108 uC  1090  108.
dt
Общее решение уравнения:
uC= uC пр + uC св.
Принужденная составляющая напряжения:
8
uC св= 1090  10 = 120 В.
9,09  108
Свободная составляющая напряжения:
uC св= Ae9, 0910 t ,
где р – корень характеристического уравнения, р= – 9,09 х 108 1/с.
Действительное значение напряжения:
8
9 , 09108 t
uC = 120 + Ae
.
Постоянная интегрирования А определяется с помощью начального
условия uC(0) = 0 = 120 + A; А= – 120.
Тогда:
9, 09108 t
uC = 120 (1– e
) В.
Токи в ветвях цепи:
8
8
du
i3  C 3 C  50  10 12 (120 )(9,09  10 8 )e 9,0910 t  5,45e 9,0910 t A;
dt
8
8
8
R3 duC u C
i2 
C

 1,82e 9,0910 t  4(1  e 9,0910 t )  4  2,18e 9,0910 t A;
R2
dt
R2
8
i1  i 2  i3  4  3,27 e 9,0910 t A.
Графики изменения напряжения токов в ветвях приведены на рис.
2.2,б.
2.2 Расчет переходных процессов в линейных электрических цепях операторным методом
Задача 1. Цепь (рис. 2.3) с R1 = 15 Ом и R2 = 60 Ом; L2 = l Гн;
R3 = 20 Ом; L3 = 2 Гн подключается к источнику U=150 В.
34
Определить законы изменения токов в ветвях цепи после ее включения.
S
R1
+
i1
R3
R2
U
L3
L2
i2
i3
Рис. 2.3. Электрическая схема
Решение.
Находим операторное сопротивление:
Z ( p)  R1 
( R2  pL2 )( R3  pL3 ) 2 p 2  185 p  2400

.
R2  pL2  R3  pL3
80  3 p
Операторный ток:
I1 ( p) 
150(3 p  80)
75(3 p  80)

.
p(2 p 2  185 p  2400) p( p 2  92,5 p  1200)
Ток i 1 ( t ) определяем с помощью теоремы разложения:
F2 ( p )=p2 + 92,5 p + 1200 = 0;
p2,3 = – 46,25  2139  1200 = – 46,25  30,64;
p1,= 0; p2 = – 15,6 1/с; р3 = – 76,89 1/с;
F1( p ) = 75 (3p+ 80);
F1(0) =6000;
F2 (О) = 1200;
F`2 ( p ) = 2p + 92,5;
F1 ( p 2) = 75 [3(–15,6) + 80] = 2487,8;
F`2 ( p 2)= 2 (–15,61)+ 92,5 = 61,28;
F1 ( p 3) = 75 [3 (–76,89) + 80] = –11 300;
F`2( p 3) =2(–76,89) + 92,5 = – 61,28;
600
2487,8

e 15,61t 
1200  15,61  61,28
 11300

e  76,89t  5  2,6e15,61t  2,4e  76,89t A.
(76,89)( 61,28)
Операторный ток во второй ветви:
i1 (t ) 
35
I 2 ( p)  I1 ( p)
R3  pL3
75(2 p  20)

;
2
R2  pL2  R3  pL3 p( p  92,5 p  1200)
F1( p ) =75(2p+20); F1(0)=1500;
F1( p 2) =75(2(–15,61)+20)=–841,5;
F1( p 3) =75(2(–76,89)+20)=–10033,5.
Токи во второй и третьей ветвях:
1500
 841
i2 (t ) 

e 15, 61t 
1200  15,61  61,28
 10033

e  75,89t  1,25 
(76,89)( 61,28)
 0,88e 15, 61t  2,1e  76,89t A;
i3  i1  i2  3,75  3,48e 15, 61t  0,27e  76,89t A.
Задача 2. Цепь (рис. 2.4) с R1 = 80 и R2 = 100 Ом; С2 = 50 мкФ;
R3 = 50 Ом; С3 = 25 мкФ подключается к источнику с U = 500 В.
Определить законы изменения токов в ветвях цепи.
S
R1
+
i1
R2
R3
U
C2
i2
-
C3
i3
Рис. 2.4. Электрическая схема
Решение.
Находим операторное сопротивление цепи:
( R  1 / pC2 )( R3  1 / pC3 ) 17 p 2  9800 p  8  105
Z ( p)  R1  2

.
R2  R3  1 / pC2  1 / pC3
p(0,15 p  60)
Операторный и действительный токи в первой ветви:
I1 ( p) 
500
p(0,15 p  60)
4,41( p  400)
 2
;
2
5
p 17 p  9800  8  10
p  576,5 p  47  103
F2 ( p ) = p2+576,5p+47*103=0;
36
p1 = –98 1/c; p2= –478 1/c;
F1( p ) = 4,41(p+400); F`2( p )=2p+576,5;
F1( p 1) = 1332; F`2( p 1)=380,5;
F1( p 2) = –344; F`2( p 2)= –380,5;
i1 (t ) 
1332  98t
e
 3,5e  478t  3,5e  98t  0,9e  478t A.
380,5
Операторный и действительный токи во второй и третьей ветвях:
I 2 ( p)  I1 ( p)
R3  1 / pC3
1,47( p  800 )
 2
R2  R3  1 / pC2  1 / pC3
p  576,5 p  47  10 3
F 1( p ) = 1,47(p+800); F1( p 1) = 1032; F2( p 2) = 473,3.
37
3. Задание
Задание №1.
Исходные данные:
Цепь, изображенная на рис. 3.1 имеет параметры, приведенные в
табл. 3.1.
Определить: токи во всех ветвях цепи после подключения ее к источнику с постоянным напряжением U. Построить графики токов.
S
L1
R1
+
R2
R3
L2
L3
U
Рис. 3.1. Электрическая схема
Таблица 3.1
Исходные данные для задания № 1
№
опыта
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
U,
B
120
200
220
220
150
100
250
220
200
200
110
220
200
220
100
300
200
220
200
220
R1,
Ом
24
10
20
15
20
20
10
10
10
5
10
12
5
4
15
20
5
18
20
L1,
Гн
0,002
1
0,01
2
2
0,02
0,002
1
38
R2,
Ом
15
25
10
20
60
10
20
20
25
10
10
10
10
10
20
50
10
20
9
L2,
Гн
1
0,2
1
1
0.5
0.2
0,002
4
1
2
1
2
1
-
R3,
Ом
10
50
5
20
20
25
10
50
2
10
40
15
60
100
30
-
L3,
Ом
2
0.1
4
0,001
2
1
0.4
0,001
0,4
1
0,004
2
0,04
1
1
1
0,004
5
4
Продолжение таблицы 3.1
№
опыта
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
U,
B
400
100
300
200
100
300
200
150
220
400
100
300
200
400
220
R1,
Ом
32
10
22
25
12
15
20
20
5
10
22
25
20
15
5
L1,
Гн
5
1
2
1
-
R2,
Ом
40
5
10
50
10
20
10
20
10
10
50
10
40
5
25
L2,
Гн
1
1
1
2
4
0,5
0,002
1
4
0,5
0,2
2
R3,
Ом
10
40
50
40
60
20
25
2
60
20
50
40
30
L3,
Ом
4
1
1
5
1
2
1
0,4
0,004
1
1
2
5
0,4
4
Задание №2.
Исходные данные:
Цепь, изображенная на рис. 3.2, имеет параметры, приведенные в
табл. 3.2.
Определить: токи в ветвях цепи после подключения ее к источнику с
постоянным напряжением U.
S
R1
L1
С1
+
R2
R3
L2
L3
С2
С3
U
-
Рис. 3.2. Электрическая схема
Таблица 3.2
Исходные данные для задания № 2
№
опыта
1
2
3
4
U,
В
100
200
100
100
R1,
Ом
100
100
-
L1,
Гн
-
С1,
мкФ
10
100
R2,
Ом
20
50
39
L2,
Гн
0,4
0,04
-
С2,
мкФ
-
R3,
Ом
-
L3,
Гн
2
4
С3,
мкФ
5
5
-
Продолжение таблицы 3.2
№
опыта
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
U,
В
110
100
100
100
100
100
200
200
100
220
100
200
100
200
400
100
200
100
200
100
200
100
200
100
400
100
R1,
Ом
100
10
100
50
5
10
10
10
100
20
50
10
10
5
50
L1,
Гн
2
1
2
4
2
5
5
0,01
1
2
5
10
2
2
2
-
С1,
мкФ
2
50
-
R2,
Ом
10
5
10
20
5
100
10
10
5
20
10
20
100
5
10
20
5
-
40
L2,
Гн
0,5
4
0,04
4
4
4
С2,
мкФ
100
10
50
200
10
5
50
-
R3,
Ом
10
20
40
10
5
4
10
40
5
10
10
5
40
-
L3,
Гн
0,02
4
5
0,025
-
С3,
мкФ
1
100
20
5
10
10
10
20
100
100
5
200
10
100
20
100
10
Список рекомендуемой литературы
Основная:
1. Теоретические основы электротехники: (переменный ток). Ч.3. / Фармаковский,
В. Л. – Л., 1972 . – 319 с.: ил. – Библиогр.: с. 316
2. Расчетно-графические задания по дисциплине "Теоретические основы электротехники": учеб. пособие / Сошинов А.Г. – Волгоград: РПК "Политехник" , 2001 . – 43с.
3. Сборник задач по теоретическим основам электротехники/ Вишняков Н.П., И.И.
Жданович, В.И. Лаппо, В.Л. Фармаковский; ЛВВИСУ. Л., 1989. 260 с.
Дополнительная:
1. Теоретические основы электротехники: В 3-х т. Учебник для вузов. Том 2. – 4-е изд.
/ К.С. Демирчян, Л.Р. Нейман, Н.В. Коровкин, В.Л. Чечурин. – СПб.: Питер, 2004-576 с.: ил.
2. Теоретические основы электротехники. Электрические цепи: Бессонов Л.А. Учебник – 10-е изд. – М.: Гардарики, 2002 – 638 с.: ил.
41
Составители:
Анатолий Григорьевич Сошинов
Татьяна Васильевна Копейкина
РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Методические указания к выполнению курсовой работы по дисциплине
«Теоретические основы электротехники»
Под редакцией авторов.
Темплан 2011 г., поз. № 17К.
Подписано в печать 17. 01. 2011 г. Формат 60×84 1/16.
Бумага листовая. Печать офсетная.
Усл. печ. л. 2,56. Уч..-изд. л. 2,81.
Тираж 50 экз. Заказ №
Волгоградский государственный технический университет
400131, г. Волгоград, пр. Ленина, 28, корп. 1.
Отпечатано в КТИ
403874, г. Камышин, ул. Ленина, 5, каб. 4.5
42