Домашнее задание № 1. Вариант 3. Методы анализа линейных

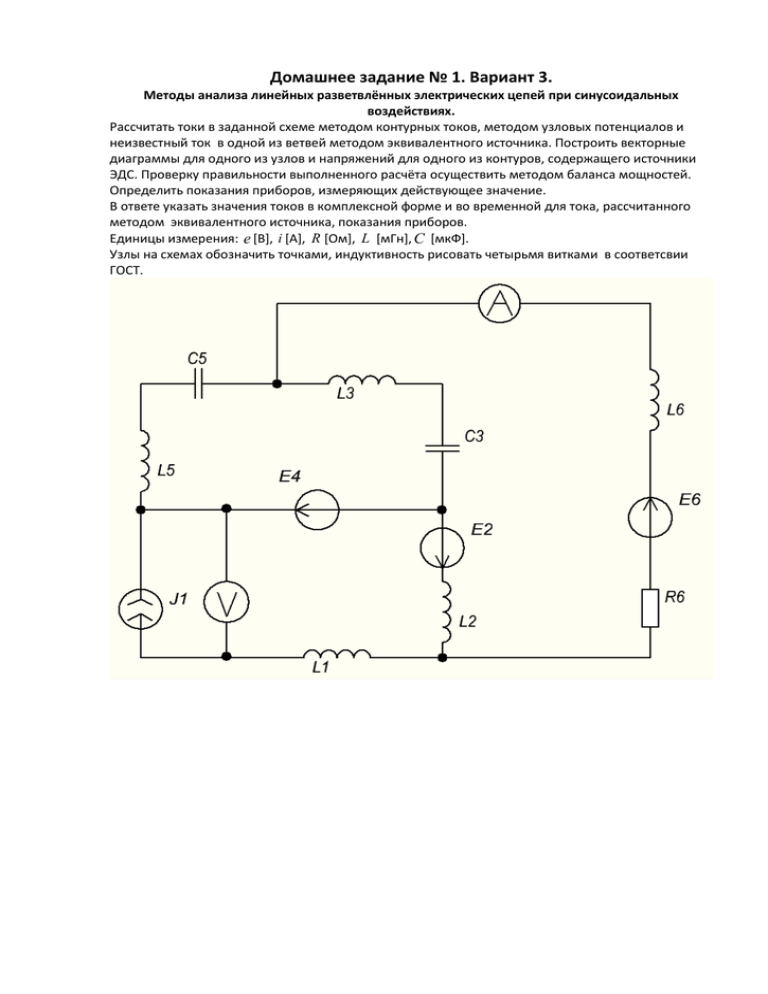
Домашнее задание № 1. Вариант 3.
Методы анализа линейных разветвлённых электрических цепей при синусоидальных
воздействиях.
Рассчитать токи в заданной схеме методом контурных токов, методом узловых потенциалов и
неизвестный ток в одной из ветвей методом эквивалентного источника. Построить векторные
диаграммы для одного из узлов и напряжений для одного из контуров, содержащего источники
ЭДС. Проверку правильности выполненного расчёта осуществить методом баланса мощностей.
Определить показания приборов, измеряющих действующее значение.
В ответе указать значения токов в комплексной форме и во временной для тока, рассчитанного
методом эквивалентного источника, показания приборов.
Единицы измерения: e [В], i [А], R [Ом], L [мГн], C [мкФ].
Узлы на схемах обозначить точками, индуктивность рисовать четырьмя витками в соответсвии
ГОСТ.
e2 (t )  200 2 sin(103 t  180 0 )
E 4  200
E 6  400  200 j
J1  2 j
R6  100 Ом
L1  100 мГн  0.1 Гн
L2  50 мГн  0.05 Гн
L3  200 мГн  0.2 Гн
L5  115 мГн  0.115 Гн
L6  100 мГн  0.1 Гн
10
10 5
мкФ 
Ф
3
3
200
2 10 4
C5 
мкФ 
Ф
3
3
Запишем e2 (t ) в комплексной форме:
C3 
  103 рад / c
e2 (t )  200 2 sin(103 t  1800 )
E 2  200
1. Метод контурных токов.
Выберем направления контурных токов так, как показано на рисунке:
Мы имеем 3 контура, один из которых содержит источник тока, поэтому ток в этом контуре
равняется I 11  J 1 . Составим уравнения для остальных контуров:
I 11  J 1


1
1 
1 
I 22  j L3  j
 j L5  j
  I 33  j L3  j
  E4
C3
C5 
C3 





1
1 
I 33  j L2  j L3  j
 R6  j L6   I 22  j L3  j
  I 11  j L2  E2  E6
C3
C3 



Учитывая первое уравнение, имеем:


1
1 
1 
I 22  j L3  j
 j L5  j
  I 33  j L3  j
  E4
C3
C5 
C3 





1
1 
I 33  j L2  j L3  j
 R6  j L6   I 22  j L3  j
  J1 j L2  E2  E6

C

C
3
3 



Подставляя значения, получим:
I 22  200 j  300 j  115 j  15 j   I 33  200 j  300 j   200
I 33  50 j  200 j  300 j  100  100 j   I 22  200 j  300 j   2 j  50 j  200  400  200 j
Из первого уравнения I 33  2 j , тогда второе уравнение примет вид:
2 j  (100  50 j )  I 22 100 j  100  200  200 j
200 j  100  I 22 100 j  100  200  200 j
I 22  4 j
Таким образом, контурные токи равняются:
I 11  2 j
I 22  4 j
I 33  2 j
Найдём токи в ветвях схемы:
I1  J1  2 j
I 2  I 11  I 33  4 j
I 3  I 22  I 33  6 j
I 4  I 22  I 11  2 j
I 5  I 22  4 j
I 6  I 33  2 j
2. Метод узловых потенциалов.
Пронумеруем узлы в соответствие с рисунком. Примем потенциал узла 0 равным нулю:  0  0 .
Тогда потенциал узла 1 равняется E4 : 1  E4 . Составим уравнения для узлов 2 и 3:




E6
1
1
1
1
1
  1 
2 


 3 

1
1
R6  j L6 
R6  j L6 R6  j L6
 j L  j 1
j L5  j
j L5  j
3



C

C

C
3
5
5


 1

E6
E
1
1

 2 
 J1
  2 
R6  j L6 j L2 R6  j L6
 j L2 R6  j L6 
3 
Учитывая, что 1  E4 , имеем:




E6
E4
1
1
1
1

2 


 3 

1
R6  j L6  j L  j 1
R6  j L6 R6  j L6
 j L  j 1
j L5  j
3
5


C3
C5
C5


 1

E6
E
1
1

 2 
 J1
  2 
j

L
R

j

L
R

j

L
j

L
R

j

L
2
6
6 
6
6
2
6
6

3 
Подставляя значения, получим:


1
1
1
200
1
400  200 j


 3 


100  100 j 100  100 j
 200 j  300 j 115 j  15 j 100  100 j  115 j  15 j
2 
 1

1
1
200 400  200 j



2j
  2 
100  100 j 50 j 100  100 j
 50 j 100  100 j 
3 
После преобразований из первого уравнения, получим:
 2  3  600
Второе уравнение примет вид:
 1
 
1
1
200 400  200 j




2j
   3  600  
50 j 100  100 j
 100  100 j
 50 j 100  100 j  
3 
Отсюда находим:
3  0
Соответственно,  2  3  600  600
Таким образом, мы получили следующие потенциалы узлов:
0  0
1  200
 2  600
3  0
Найдём токи в ветвях электрической цепи:
I2 
I3 
I5 
I6 
0  3  E2
200

4j
j L2
50 j
 2  0
j L3  j
1
C3
1  2
j L5  j
1
C5

600
6j
100 j

400
4j
100 j
3  2  E6 200  200 j

2j
R6  j L6
100  100 j
Так как ток в 1-ой ветви равняется I1  J1  2 j , а по первому уравнению Кирхгофа для узла 1
имеем:
I1  I 4  I 5  0
Тогда найдём ток I 4 :
I 4  I 5  I1  4 j  2 j  2 j
Таким образом, мы получили значения токов в ветвях:
I1  2 j
I2  4 j
I3  6 j
I4  2 j
I5  4 j
I6  2 j
что соответствует найденным значениям по методу контурных токов.
3. Метод эквивалентного источника.
Найдём ток в 5-ой ветви методом эквивалентного источника.
Найдём напряжение холостого хода U 12 . Введём контурные токи I 11 и I 22 так как показано на
рисунке. Так как контур 1 содержит источник тока, то I 11  J 1  2 j . Составим уравнение для
второго контура:

I 22  j L2  j L3 


I 22  j L2  j L3 

j

1
 j L6  R6   I 22  j L2  E 2  E 6
C3

j

1
 j L6  R6   J 1 j L2  E 2  E 6
C3

Подставляя значения, получим:
I 22  50 j  200 j  300 j  100 j  100   2 j  50 j  200  400  200 j
300  200 j 16 2
I 22 
  j
100  50 j
5 5
16 2
 j . По второму закону Кирхгофа:
Ток I 3  I 22 
5 5

1 
I 3  j L3  j
  U 12  E 4
C3 

Откуда найдём U 12 :

1 
U 12  E 4  I 3  j L3  j

C3 

 16 2 
U 12  200    j   200 j  300 j   160  320 j
 5 5 
Найдём входное сопротивление относительно точек 2 и 1:

1 
 j L3  j
  R6  j L2  j L6 

C
3 
Z вх  
1
j L3  j
 R6  j L2  j L6
C3
Zвх 
 200 j  300 j 100  50 j  100 j   80  140 j
200 j  300 j  100  50 j  100 j
Теперь найдём ток в 5-ой ветви:
U 12
U 12

Z вх  Z5 Z  j L  j 1
вх
5
C5
160  320 j
160  320 j
I5 

4j
80  140 j  115 j  15 j
80  40 j
I5 
что совпадает с результатам, полученными методом контурных токов и узловых потенциалов.
Ток I 5 во временной форме:
I5 (t )  4 2 sin(103 t  900 )
4. Векторные диаграммы.
Построим векторную диаграмму для токов для узла 0. По первому закону Кирхгофа:
I3 I 2 I 4  0
I2  4 j
I3  6 j
I4  2 j
Построим векторную диаграмму напряжений для контура 0-3-2. По второму закону Кирхгофа:

1 
I 3  j L3  j
  I 2  j L2  I 6  R6  j L6   E 2  E 6
C3 

Токи в ветвях равняются:
I2  4 j
I3  6 j
I6  2 j
5. Показания приборов.
Амперметр в ветви 6 показывает действующее значение тока I 6  2 j , поэтому его показания
равняются 2 А. Найдём показания вольтметра.
Методом узловых потенциалов мы нашли:
1  200
3  0

1  3  J1  j L1  U 14  0

Откуда найдём напряжение U 14 :

U 14  1  3  J1  j L1  200  2 j 100 j  0
Таким образом, вольтметр покажет 0 В.
6. Баланс мощностей.
Токи во всех ветвях схемы:
I1  2 j
I2  4 j
I3  6 j
I4  2 j
I5  4 j
I6  2 j
Полная комплексная мощность источников-генераторов должна равняться полной комплексной
мощности потребителей. Рассчитаем полную комплексную мощность источников-генераторов.
Источниками-генераторами являются E2 , E4 , E6 , так как направление тока в них совпадает с
направлением ЭДС. Источником-генератором является и источник тока, так как напряжение на
нём U 14 противоположно направлению J 1 . Но так как напряжение на источнике тока
(показания вольтметра) равно нулю, то генерируемая источником тока J 1 мощность также
равняется нулю. Таким образом, полная комплексная мощность источников-генераторов
равняется:
*
*
*
S ИГ  E2 I 2  E4 I 4  E6 I 6
S ИГ  200  (4 j )  200  (2 j )  (400  200 j )(2 j )  400  400 j
Полная комплексная мощность потребителей (мощность, потребляемая J 1 равняется нулю):
2
2
S П  J1  j L1  I 2  j L2  I 3
2
2
2


1 
1 
 j L3  j
  I  j L5  j
  I  R6  j L6 
C3  5 
C5  6

S П  4 100 j  16  50 j  36  (200 j  300 j)  16  (115 j 15 j)  4  (100  100 j)  400  400 j
Таким образом: S ИГ  S П , значит, баланс мощностей сходится.
Ответ:
Значения токов в комплексной форме:
I1  2 j
I2  4 j
I3  6 j
I4  2 j
I5  4 j
I6  2 j
Ток I 5 во временной форме:
I5 (t )  4 2 sin(103 t  900 )
Показание вольтметра 0 В. Показание амперметра 2 А.