учебника 10 класса, профильный уровень, ФК ГОС
реклама
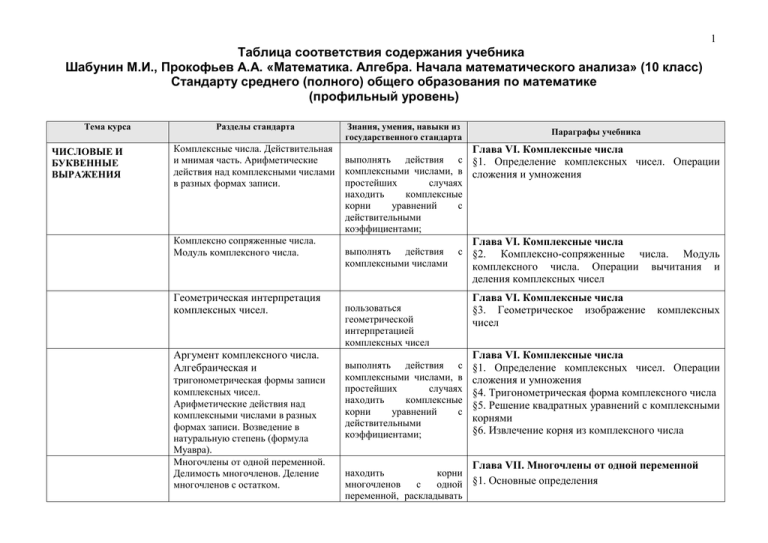
1 Таблица соответствия содержания учебника Шабунин М.И., Прокофьев А.А. «Математика. Алгебра. Начала математического анализа» (10 класс) Стандарту среднего (полного) общего образования по математике (профильный уровень) Тема курса ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ Разделы стандарта Знания, умения, навыки из государственного стандарта Параграфы учебника Комплексные числа. Действительная выполнять действия с и мнимая часть. Арифметические действия над комплексными числами комплексными числами, в простейших случаях в разных формах записи. находить комплексные корни уравнений с действительными коэффициентами; Комплексно сопряженные числа. выполнять действия с Модуль комплексного числа. комплексными числами Глава VI. Комплексные числа §1. Определение комплексных чисел. Операции сложения и умножения Геометрическая интерпретация комплексных чисел. Глава VI. Комплексные числа §3. Геометрическое изображение чисел Аргумент комплексного числа. Алгебраическая и тригонометрическая формы записи комплексных чисел. Арифметические действия над комплексными числами в разных формах записи. Возведение в натуральную степень (формула Муавра). Многочлены от одной переменной. Делимость многочленов. Деление многочленов с остатком. пользоваться геометрической интерпретацией комплексных чисел выполнять действия с комплексными числами, в простейших случаях находить комплексные корни уравнений с действительными коэффициентами; Глава VI. Комплексные числа §2. Комплексно-сопряженные числа. Модуль комплексного числа. Операции вычитания и деления комплексных чисел комплексных Глава VI. Комплексные числа §1. Определение комплексных чисел. Операции сложения и умножения §4. Тригонометрическая форма комплексного числа §5. Решение квадратных уравнений с комплексными корнями §6. Извлечение корня из комплексного числа Глава VII. Многочлены от одной переменной находить корни многочленов с одной §1. Основные определения переменной, раскладывать 2 Тема курса Разделы стандарта Знания, умения, навыки из государственного стандарта многочлены множители; Схема Горнера. Теорема Безу. Число корней многочлена. Основная теорема алгебры. Рациональные корни многочленов с целыми коэффициентами. Многочлены от двух переменных. Формулы сокращенного умножения для старших степеней. Многочлены от нескольких переменных, симметрические многочлены. Корень степени n>1 и его свойства. Степень с рациональным показателем и ее свойства. Понятие о степени с действительным показателем. Свойства степени с действительным показателем. Параграфы учебника на Глава VII. Многочлены от одной переменной находить корни многочленов с одной §2. Схема Горнера переменной, раскладывать многочлены на множители; Глава VII. Многочлены от одной переменной находить корни многочленов с одной §3. Теорема Безу. Корни многочлена переменной, раскладывать многочлены на множители; Глава VII. Многочлены от одной переменной находить корни многочленов с одной §4. Алгебраические уравнения переменной, раскладывать многочлены на множители; Глава VIII. Многочлены от одной переменной §3. Нелинейные системы уравнений с двумя неизвестными §4. Нелинейные системы с тремя неизвестными Глава II. Числовые множества находить значения корня натуральной степени, §3. Степени и корни используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах; 3 Тема курса Разделы стандарта Логарифм числа. Основное логарифмическое тождество. Логарифм произведения, частного, степени; переход к новому основанию. Десятичный и натуральный логарифмы, число е. Преобразования выражений, включающих арифметические операции, а также операции возведения в степень и логарифмирования. ТРИГОНОМЕТРИЯ Радианная мера угла. Синус, косинус, тангенс, котангенс произвольного угла. Синус, косинус, тангенс и котангенс числа. Знания, умения, навыки из государственного стандарта Параграфы учебника Глава II. Числовые множества находить значения логарифма, используя при §4. Логарифмы необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах; Глава II. Числовые множества §2. Натуральные, целые, рациональные и иррациональные числа §3. Степени и корни §4. Логарифмы Глава IX. Предел и непрерывность функции §1. Точные грани числовых множеств. Операции над действительными числами производить практические Глава V. Тригонометрические формулы расчеты по формулам, §1. Тригонометрическая окружность. Градусная и включая формулы, радианная меры измерения угловых величин содержащие §2. Координаты точек тригонометрической тригонометрические окружности проводить преобразования числовых и буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции; функции, используя при необходимости справочные материалы и простейшие вычислительные устройства; определять значение Глава V. Тригонометрические формулы функции по значению §3. Синус, косинус, тангенс и котангенс аргумента при различных способах задания функции; строить графики 4 Тема курса Разделы стандарта Знания, умения, навыки из государственного стандарта Параграфы учебника изученных функций, выполнять преобразования графиков; Основные тригонометрические тождества. Преобразования тригонометрических выражений. Синус, косинус и тангенс суммы и разности двух углов. Формулы приведения. Синус и косинус двойного угла. Формулы половинного угла. Преобразования суммы тригонометрических функций в произведение и произведения в сумму. Арксинус, арккосинус, арктангенс, арккотангенс числа. ФУНКЦИИ Функции. Область определения и множество значений. График функции. Сложная функция (композиция функций). Свойства функций: монотонность, четность и нечетность, периодичность, ограниченность. Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума Глава V. Тригонометрические формулы проводить преобразования §4. Преобразование тригонометрических числовых и буквенных выражений. Доказательство тождеств выражений, включающих тригонометрические функции; проводить преобразования числовых и буквенных выражений, включающих тригонометрические функции; Глава V. Тригонометрические формулы §5.Формулы сложения §6. Формулы приведения §7. Формулы кратных углов §8. Формулы половинных углов §9. Формулы преобразования произведений в суммы §10. Формулы преобразования сумм в произведение Глава V. Тригонометрические формулы арктангенс проводить преобразования §11. Арксинус, арккосинус, числовых и буквенных арккотангенс числа выражений, включающих тригонометрические функции; Глава III. Функции определять значение функции по значению §1. Линейная, квадратичная и дробно-линейная аргумента при различных функции способах задания §2. Основные понятия, относящиеся к числовым функции; функциям Глава III. Функции описывать по графику и по формуле поведение и §3. Свойства функций свойства функций; и 5 Тема курса Разделы стандарта Знания, умения, навыки из государственного стандарта Параграфы учебника (локального максимума и минимума). Взаимно обратные функции. Область определения и область значений обратной функции. График обратной функции. Нахождение функции, обратной данной. Построение графиков функций, заданных различными способами. Преобразования графиков: параллельный перенос, симметрия относительно осей координат и симметрия относительно начала координат, симметрия относительно прямой y = x, растяжение и сжатие вдоль осей координат. Степенная функция с натуральным показателем, ее свойства и график. Вертикальные и горизонтальные асимптоты графиков. Графики дробнолинейных функций. строить графики Глава III. Функции изученных функций, §4. Обратная функция выполнять преобразования графиков; описывать по графику и по формуле поведение и свойства функций; Глава III. Функции строить графики §5. Графики функций изученных функций, выполнять преобразования графиков; X. Степенная, строить графики Глава логарифмическая функции изученных функций, выполнять преобразования §1. Степенная функция графиков; показательная и описывать по графику и по формуле поведение и свойства функций; строить графики Глава III. Функции изученных функций, §1. Линейная, квадратичная и дробно-линейная выполнять преобразования функции графиков; 6 Тема курса Разделы стандарта Знания, умения, навыки из государственного стандарта Параграфы учебника описывать по графику и по формуле поведение и свойства функций; Показательная функция (экспонента), ее свойства и график. Логарифмическая функция, ее свойства и график. X. Степенная, строить графики Глава логарифмическая функции изученных функций, выполнять преобразования §2. Показательная функция графиков; показательная и описывать по графику и по формуле поведение и свойства функций; X. Степенная, показательная строить графики Глава логарифмическая функции изученных функций, выполнять преобразования §3. Логарифмическая функция графиков; и описывать по графику и по формуле поведение и свойства функций; Бесконечно убывающая Глава II. Числовые множества НАЧАЛА находить сумму геометрическая прогрессия и ее §5. Суммирование МАТЕМАТИЧЕСКОГО бесконечно убывающей сумма. АНАЛИЗА геометрический прогрессии; Понятие о пределе последовательности. Существование предела монотонной ограниченной последовательности. Теоремы о пределах последовательностей. Глава IX. Предел и непрерывность функции §2. Предел последовательности Понятие о пределе функции в точке. Поведение функций на бесконечности. Глава IX. Предел и непрерывность функции §3. Предел функции §5. Вычисление пределов функций 7 Тема курса Разделы стандарта Знания, умения, навыки из государственного стандарта Понятие о непрерывности функции. Основные теоремы о непрерывных функциях. УРАВНЕНИЯ И НЕРАВЕНСТВА Решение уравнений. уравнений. Решение уравнений Решение уравнений Решение уравнений Параграфы учебника Глава IX. Предел и непрерывность функции §4. Непрерывность функции рациональных Равносильность решать уравнения Глава IV. Алгебраические уравнения и неравенства §1. Уравнение и его корни. Преобразование уравнений. §2. Квадратные уравнения и сводящиеся к ним иррациональных Глава IV. Алгебраические уравнения и решать иррациональные неравенства уравнения §3. Иррациональные уравнения. Уравнения, содержащие знак модуля показательных логарифмических Решение рациональных и иррациональных неравенств. Метод интервалов. Доказательства неравенств. Неравенство о среднем арифметическом и среднем геометрическом двух чисел решать уравнения рациональные Глава X. Степенная, показательные логарифмическая функции показательная и показательная и §4. Показательные уравнения Глава X. Степенная, решать логарифмические логарифмическая функции уравнения §5. Логарифмические уравнения решать рациональные иррациональные неравенства доказывать неравенства Глава II. Числовые множества и §6. Числовые неравенства Глава IV. Алгебраические неравенства §4. Алгебраические неравенства несложные уравнения и Решение показательных и Глава X. Степенная, показательная и решать показательные и логарифмических неравенств. логарифмическая функции логарифмические §6. Показательные и логарифмические неравенства неравенства 8 Тема курса Разделы стандарта Знания, умения, навыки из государственного стандарта Равносильность систем Решение систем уравнений с двумя неизвестными (простейшие типы). Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных. Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений. Параграфы учебника Глава VIII. Многочлены от одной переменной §1. Основные понятия, связанные с системами уравнений Глава VIII. Многочлены от одной переменной решать рациональные, §2. Системы линейных уравнений показательные и логарифмические уравнения и неравенства, иррациональные и тригонометрические уравнения, их системы; Глава I. Элементы математической логики §1. Высказывания и операции над ними §2. Неопределенные высказывания. Знаки общности и существования §3. Некоторые приемы доказательства Глава II. Числовые множества §1. Множества. Операции над множествами. решать уравнения, Глава V. Тригонометрические формулы неравенства и системы с §1. Тригонометрическая окружность. Градусная и применением графических радианная меры измерения угловых величин решать текстовые задачи с помощью составления уравнений, и неравенств, интерпретируя результат с учетом ограничений условия задачи; представлений, свойств функций, производной; ЭЛЕМЕНТЫ КОМБИНАТОРИКИ, СТАТИСТИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ Формула бинома Ньютона. Глава II. Числовые множества Свойства биномиальных вычислять коэффициенты §5. Суммирование бинома Ньютона по коэффициентов. формуле и с использованием треугольника Паскаля;