Задание: Спроектировать привод ленточного транспортера.

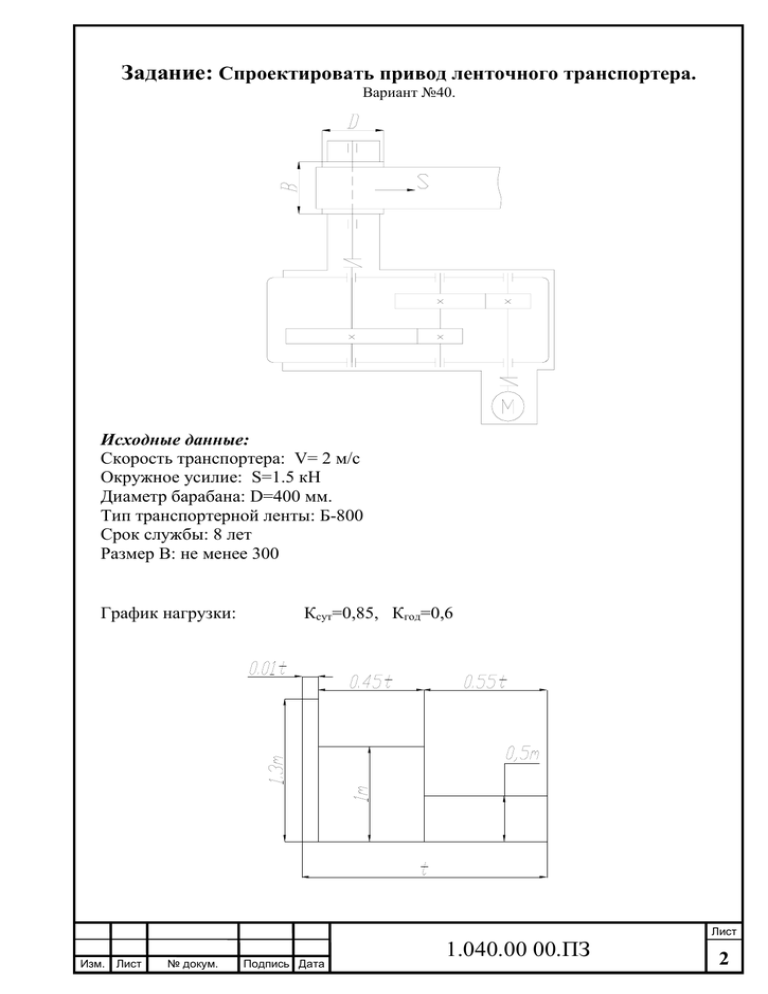
Задание: Спроектировать привод ленточного транспортера.
Вариант №40.
Исходные данные:
Скорость транспортера: V= 2 м/с
Окружное усилие: S=1.5 кН
Диаметр барабана: D=400 мм.
Тип транспортерной ленты: Б-800
Срок службы: 8 лет
Размер В: не менее 300
График нагрузки:
Ксут=0,85, Кгод=0,6
Лист
Изм. Лист
№ докум.
Подпись Дата
1.040.00 00.ПЗ
2
ВВЕДЕНИЕ.
Цель курсового проектирования – систематизировать, закрепить,
расширить теоретические знания, а также развить расчетно-графические
навыки студентов. Основные требования, предъявляемые к создаваемой
машине: высокая производительность, надежность, технологичность,
минимальные габариты и масса, удобство в эксплуатации и экономичность. В
проектируемом редукторе используются зубчатые передачи.
Редуктором называют механизм, состоящий из зубчатых или
червячных передач, выполненный в виде отдельного агрегата и служащий для
передачи мощности от двигателя к рабочей машине.
Назначение редуктора – понижение угловой скорости и повышение
вращающего момента ведомого вала по сравнению с валом ведущим.
Нам в нашей работе необходимо спроектировать редуктор для
ленточного транспортера, а также подобрать муфты, двигатель. Редуктор
состоит из литого чугунного корпуса, в котором помещены элементы передачи
– 2 шестерни, 2 колеса, подшипники, валы и пр. Входной вал посредством
муфты соединяется с двигателем, выходной также посредством муфты с
транспортером.
Лист
Изм. Лист
№ докум.
Подпись Дата
1.040.00 00.ПЗ
3
1. Выбор электродвигателя и кинематический расчет.
Кинематический анализ схемы привода.
Привод состоит из электродвигателя, двухступенчатого редуктора. При
передаче мощности имеют место ее потери на преодоление сил вредного
сопротивления. Такие сопротивления имеют место и в нашем приводе: в
зубчатой передаче, в опорах валов, в муфтах и в ремнях с роликами. Ввиду
этого мощность на приводном валу будет меньше мощности, развиваемой
двигателем, на величину потерь.
1.1 Коэффициент полезного действия привода.
По таблице 1.1 [1] коэффициент полезного действия пары цилиндрических колес ηз.к. = 0,98; коэффициент, учитывающий потери пары
подшипников качения, ηп = 0,99; коэффициент, учитывающий потери в
муфте ηм = 0,98; коэффициент, учитывающий потери в ремне с роликами
ηр = 0,9
1   з.к п  м  р
1   з.к. п  м  0,98*0,99*0,98 = 0,95
2  1  з.к. п  0,95*0,98*0,99 = 0,92
3  2 п  0,92*0,99 = 0,91
Общий КПД привода:
 з2.к. п5  м2  р.
 = 0,982 * 0,995 * 0,982*0,9 = 0,8
1.2 Выбор электродвигателя.
Мощность на валу барабана:
Рб=S*V=1.5*2=3 кВт ,
где S-окружное усилие;
V-скорость транспортера;
Требуемая мощность электродвигателя:
Ртр=Рб/ =3/0,8=3,75 кВт,
Угловая скорость барабана:
 б  2V / Dб  2  2 / 0,4  10 рад / с ,
Частота вращения барабана:
nб  30 б /   30  10 / 3,14  95,5об / мин
При выборе электродвигателя
транспортера с полной загрузкой.
учитываем
возможность
пуска
Лист
Изм. Лист
№ докум.
Подпись Дата
1.040.00 00.ПЗ
4
Пусковая требуемая мощность:
Рп=Ртр*1,3м=3,75*1,3=4,875 кВт
Эквивалентная мощность по графику загрузки:
Tэкв  3 1,33  0,01  1  0,45  0,5 3  0,55  0,81
Pэкв  Т экв  Ртр  0,81  3,75  3,04 кВт
По ГОСТ 19523-81 (см. табл. П1 приложения [1]) по требуемой мощности
Ртр = 3,75 кВт выбираем электродвигатель трехфазный асинхронный
короткозамкнутый серии 4АН закрытый, обдуваемый с синхронной частотой
n = 1500 об/мин 4АН100S4 с параметрами Рдв = 3 кВт и скольжением
S=4,4 %, отношение Рп/Рн=2. Рпуск=2*3=6 кВт-мощность данного двигателя на
пуске она больше чем нам требуется Рп=4,875 кВт.
Номинальная частота вращения двигателя:
 100  s 
n дв  n

 100 
где: nдв – фактическая частота вращения двигателя, мин-1;
n – частота вращения, мин-1;
s – скольжение, %;
 100  s 
 100  4,4 
1
nдв  n
  1500
  1434 мин
 100 
 100 
Передаточное отношение редуктора:
U=nдв/nб=1434/95,5=15
Передаточное отношение первой ступени примем u1=5; соответственно
второй ступени u2=u/u1=15/5=3
1.3 Крутящие моменты.
Момент на входном валу:
Т1 
Ртр
 дв
,
где: Ртр – требуемая мощность двигателя, кВт;
 дв – угловая скорость вращения двигателя, об/мин;
 дв 
 nдв
30

3,14  1434
 150 рад / с
30
где: nдв – частота вращения двигателя, мин-1;
Т1 
3,75  10 3
 25 Нм  25  10 3 Нмм
150
Момент на промежуточном валу:
Т2 = Т1 * u1 * η2
где: u1 – передаточное отношение первой ступени;
η2 – КПД второго вала;
Лист
Изм. Лист
№ докум.
Подпись Дата
1.040.00 00.ПЗ
5
Т2 = 25*103 * 5*0,92 = 115*103 Нмм
Угловая скорость промежуточного вала:
 2   дв / u1  150 / 5  30 рад / с
Момент на выходном валу:
Т3 = Т2 * u2 * η3
где: u2 – передаточное отношение второй ступени;
η3 – КПД третьего вала;
Т3 = 115*103 * 3 * 0,91 = 314*103 Нмм
Угловая скорость выходного вала:
 3   б  10 рад / с
Все данные сводим в таблицу 1:
таблица 1
Частота вращения, об/мин
Угловая скорость, рад/с
Крутящий момент, 103 Нмм
Быстроходный
вал
Промежуточный
вал
Тихоходный
вал
n1= 1434
w1= 150
T1= 25
n2=286,8
w2 =30
T2= 115
n3=95,5
w3= 10
T3= 314
Лист
Изм. Лист
№ докум.
Подпись Дата
1.040.00 00.ПЗ
6
2. Расчет зубчатых колес.
2.1 Выбор материала.
Выбираем материал со средними механическими характеристиками: для
шестерни сталь 45, термическая обработка – улучшение, твердость НВ 230; для
колеса – сталь 45, термическая обработка – улучшение, но на 30 единиц ниже
НВ 200.
Допускаемые контактные напряжения по формуле (3.9 [1])

K
 H   H lim b HL , МПа
S H 
где: σН lim b – предел контактной выносливости, МПа;
 H limb  2HB  70 , МПа
 H limb  2HB  70 = 2*200 + 70 = 470 МПа
для колеса:
для шестерни:  H limb  2HB  70 = 2*230 + 70 = 530 Мпа
КНL – коэффициент долговечности
К HL  6
N HO
8  365  16  0.85  0.6  60  1434
6
 2.3 ,
N HE
10 7
где: NHO – базовое число циклов напряжений;
NНЕ – число циклов перемены напряжений;
Так как, число нагружения каждого зуба колеса больше базового, то
принимают КHL = 1.
[SH] – коэффициент безопасности, для колес нормализованной и
улучшенной стали принимают [SH] = 1,1  1,2.
530  1
 481МПа
1,1
470  1
Для колеса:  Н 2  
 428 МПа
1,1
Для шестерни:  Н 1  
Тогда расчетное контактное напряжение определяем по формуле (3.10 [1])
 Н   0,45( Н1    Н 2 )
 Н  = 0.45(481+428)=410 МПа.
2.2 Расчет быстроходной ступени двухступенчатого зубчатого редуктора.
2.2.1 Межосевое расстояние определяем по формуле (3.7 [1])
а w  К а (u1  1)3
Т 2  К Н
 Н 2  u12  ba
, мм
где: Ка – для косозубых колес Ка = 43;
u1 – передаточное отношение первой ступени;
Т2 – крутящий момент второго вала, Нмм;
Лист
Изм. Лист
№ докум.
Подпись Дата
1.040.00 00.ПЗ
7
КНβ – коэффициент, учитывающий не равномерность
распределения нагрузки по ширине венца.
При проектировании зубчатых закрытых передач редукторного типа
принимают значение КНβ по таблице 3.1 [1]. КНβ=1,25
[σH] – предельно допускаемое напряжение;
ψba – коэффициент отношения зубчатого венца к межосевому
расстоянию, для косозубой передачи ψba = 0,25  0,40.
а w  К а (u1  1)3
Т 2  К Н
 43 (5  1)3
 Н 2  u12  ba
115  10 3  1,25
 113.6 мм
410 2  5 2  0,4
Ближайшее значение межосевого расстояния по ГОСТ 2185-66 аw = 112 мм
(см. с.36 [1]).
2.2.2 Нормальный модуль:
mn = (0,01  0,02)*аw
где: аw – межосевое расстояние, мм;
mn = (0,01  0,02)*аw = (0,01  0,02)*112 = 1,12  2,24 мм
Принимаем по ГОСТ 9563-60 mn = 1,5.
Предварительно примем угол наклона зубьев β=10°.
2.2.3 Число зубьев шестерни (формула 3.12 [1] ):
z1 
2a w  cos 
,
(u1  1)mn
где: аw – межосевое расстояние, мм;
β – угол наклона зуба, °;
u1 – передаточное отношение первой ступени;
mn – нормальный модуль, мм;
2a w  cos  2  112  сos10

 24
(u1  1)mn
(5  1)1.5
z1 
2.2.4 Число зубьев колеса:
z2 = z1 * u1 = 24*5=120
2.2.5 Уточняем значение угла наклона зубьев:
cos  
z1  z 2 mn ,
2a w
где: z1 – число зубьев шестерни;
z2 – число зубьев колеса;
mn – нормальный модуль, мм;
аw – межосевое расстояние, мм;
cos  
z1  z 2 mn
2a w

(24  120)1.5
 0,9643
2  112
β = 15,36°=15о22/
2.2.6 Диаметры делительные.
Для шестерни: d1 
mn
1.5
z1 
24  37.3 мм
cos 
0,9643
Лист
Изм. Лист
№ докум.
Подпись Дата
1.040.00 00.ПЗ
8
mn
1.5
z2 
120  186.7 мм
cos 
0,9643
d  d 2 37.3  186.7
aw  1

 112 мм
2
2
Для колеса:
d2 
Проверка:
2.2.7 Диаметры вершин зубьев.
Для шестерни: da1 =d1+2mn =37,3 + 2*1,5 = 40,3 мм
Для колеса:
da2 =d2+2mn = 186,7 + 2*1,5 = 189,7 мм
2.2.8 Ширина зуба.
Для колеса:
b2 = ψba * aw = 0,4 * 112 = 45 мм
Для шестерни: b1 = b2 + 5 = 44,8 + 5 = 50 мм
2.2.9 Коэффициент ширины шестерни по диаметру.
b
 bd  1 ,
d1
где: b1 – ширина зуба для шестерни, мм;
d1 – делительный диаметр шестерни, мм;
 bd 
b1
50

 1,34
d1 37.3
2.2.10 Окружная скорость колес.

1  d 1
2

150  37.3
 2.8 м/с
2  10 3
Степень точности передачи: для косозубых колес при скорости до 10 м/с
следует принять 8-ю степень точности.
2.2.11 Коэффициент нагрузки.
К Н  К Н К Н К НV
По таблице 3.5 [1] при ψbd = 1,34, твердости НВ< 350 и несимметричном расположении колес коэффициент КНβ = 1,17.
По таблице 3.4 [1] при ν = 2,8 м/с и 8-й степени точности коэффициент
КНα=1,07.
По таблице 3.6 [1] для косозубых колес при скорости менее 5 м/с коэффициент КНυ = 1.
К Н  К Н К Н К НV = 1,17 * 1,07 * 1 = 1,252
2.2.12 Проверяем контактные напряжения по формуле 3.6 [1].
Н 
270 T2  K H (u1  1) 3
, МПа
аw
b2  u12
где: аw – межосевое расстояние, мм;
Т2 – крутящий момент второго вала, Нмм;
Лист
Изм. Лист
№ докум.
Подпись Дата
1.040.00 00.ПЗ
9
КН – коэффициент нагрузки;
u1 - передаточное отношение первой ступени;
b2 – ширина колеса, мм;
Н
270 T2  K H (u 2  1) 3 270 115  10 3  1,252(5  1) 3


 401.7 МПа   Н   410 МПа
аw
112
b2  u 22
45  5 2
Условие прочности выполнено.
2.2.13 Силы, действующие в зацеплении.
В зацеплении действуют три силы:
- Окружная
Ft 
2T1
,Н
d1
где: Т1 – крутящий момент ведущего вала, Нмм;
d1 –делительный диаметр шестерни, мм;
Ft 
2  25  10 3
 1340.5 Н
37.3
- Радиальная
Fr  Ft
tg
,Н
cos 
где: α – угол зацепления, °;
β – угол наклона зуба, °;
Fr  1340.5
tg 20
 506 Н
0,9643
- Осевая
Fa = Ft * tg β, Н
Fa = Ft * tg β = 1340,5 * 0.275 = 368 Н
2.2.14
Проверка зубьев на выносливость по напряжениям изгиба
( см. формулу 3.25 [1] ).
F 
Ft  K F  YF  K F
, МПа
b  mn
где: Ft – окружная сила, Н;
Коэффициент нагрузки КF = KFβ * KFν ( см. стр. 42 [1])
По таблице 3.7 [1] при ψbd = 1,34, твердости НВ ‹ 350 и несимметричном расположении зубчатых колес относительно опор коэффициент КFβ = 1.36.
По таблице 3.8 [1] для косозубых колес 8-й степени точности и скорости 2,8
м/с коэффициент КFυ = 1,1.
Таким образом, КF = 1,36 * 1,1 = 1,496.
Коэффициент, учитывающий форму зуба, YF зависит от эквивалентного
числа зубьев zυ
- У шестерни z 
z1
24

 28
3
cos  0.96433
Лист
Изм. Лист
№ докум.
Подпись Дата
1.040.00 00.ПЗ
10
- У колеса
z 
z2
120

 134
3
cos  0.96433
Коэффициент YF1 = 3,85 и YF2 = 3,6 (см. стр. 42 [1] ).
Определяем коэффициенты Yβ и КFα .
К F

15.36
 0,89
140
140
4  (   1)( n  5) 4  (1.5  1)(8  5)


 0.92 ,
4 
41.5
Y  1 
 1
где средние значения коэффициента торцевого перекрытия ε α = 1,5; степень
точности n = 8.
Допускаемые напряжение при проверке на изгиб определяют по формуле
3.24 [1]:
 0F lim b
, МПа
 F  
S F 
По таблице 3.9 для стали 45 улучшенной предел выносливости при отнулевом цикле изгиба  0F lim b = 1,8 НВ.
Для шестерни  0F lim b = 1,8 * 230 = 414 МПа
Для колеса
 0F lim b = 1,8 * 200 = 360 МПа
Коэффициент безопасности S F   S F '  S F "
По таблице 3.9 [1] [SF]’ = 1.75 для стали 45 улучшенной; [SF]” = 1 для
поковок и штамповок.
S F   S F '  S F "  1,75 1  1,75
Допускаемые напряжения:
Для шестерни
Для колеса
 F  
 F0
limb

414
 236.6 МПа
1,75
 F  
 F0
limb

360
 205.7 МПа
1,75
S F 
S F 
Проверку на изгиб следует проводить для того зубчатого колеса, для
 
которого отношение F меньше. Найдем отношения:
YF
Для шестерни
Для колеса
236.6
 61.45 МПа
3.85
205.7
 57 МПа
3 .6
Проверку на изгиб проводим для колеса:
F 
Ft  K F  YF  K F 1340.5  1,496  3,6  0,92

 98.8МПа  205.7 МПа
b2  mn
44.8  1.5
Условие прочности выполнено.
Лист
Изм. Лист
№ докум.
Подпись Дата
1.040.00 00.ПЗ
11
2.3 Расчет тихоходной ступени двухступенчатого зубчатого редуктора.
2.3.1 Межосевое расстояние определяем по формуле (3.7 [1])
а w  К а (u 2  1)3
Т 3  К Н
 Н 2  u 22  ba
, мм
где: Ка = 43;
u3 – передаточное отношение на выходе;
Т3 – крутящий момент на выходе;
КНβ=1.25
ψba = 0,25  0,40.
а w  43 (3  1)3
314  10 3  1,25
 148 мм
410 2  32  0,4
Ближайшее значение межосевого расстояния по ГОСТ 2185-66 аw = 140 мм
(см. с.36 [1]).
2.3.2 Нормальный модуль.
mn = (0,01  0,02)*аw = (0,01  0,02)*140 = 1.4  2.8 мм
Принимаем по ГОСТ 9563-60 mn = 1.75 мм
Предварительно примем угол наклона зубьев β=10°.
2.3.3 Число зубьев шестерни (формула 3.12 [1] )
z3 
2a w  cos  2  140  cos10

 39
(u 2  1)mn
(3  1)1.75
2.3.4 Число зубьев колеса
Z4 = z3 * u2 = 39*3=117
2.3.5
Уточняем значение угла наклона зубьев.
cos  
2.3.6
z3  z 4 mn
2a w

(39  117)1.75
 0,975
2  140
β = 12,83°=12o50/
Диаметры делительные.
mn
1.75
z3 
39  70 мм
cos 
0,975
mn
1.75
d4 
z4 
117  210 мм
cos 
0,975
d  d 4 70  210
aw  3

 140 мм
2
2
Для шестерни: d 3 
Для колеса:
Проверка:
2.3.7 Диаметры вершин зубьев.
Для шестерни: da1 =d1+2mn =70 + 2*1.75 = 73.5 мм
Для колеса:
da2 =d2+2mn = 210 + 2*1.75 = 213.5 мм
Лист
Изм. Лист
№ докум.
Подпись Дата
1.040.00 00.ПЗ
12
2.3.8 Ширина зуба.
Для колеса:
b4 = ψba aw = 0,4 * 140 = 60 мм
Для шестерни: b3 = b4 + 5 = 56 + 5 = 65 мм
2.3.9
Коэффициент ширины шестерни по диаметру.
 bd 
b3 65

 0.93
d 3 70
2.3.10 Окружная скорость колес.

2  d3
2  10
3

30  70
 1.05 , м/с
2  10 3
Степень точности передачи: для косозубых колес при скорости до 10 м/с
следует принять 8-ю степень точности.
2.3.11 Коэффициент нагрузки.
К Н  К Н К Н К НV
По таблице 3.5 [1] при ψbd = 0,93, твердости НВ< 350 и несимметричном расположении колес коэффициент КНβ = 1,1.
По таблице 3.4 [1] при ν = 1,05 м/с и 8-й степени точности коэффициент
КНα=1,06.
По таблице 3.6 [1] для косозубых колес при скорости более 1,05 м/с
коэффициент КНυ = 1.
К Н  К Н К Н К НV = 1,1 * 1,06 * 1 = 1,15
2.3.12 Проверяем контактные напряжения по формуле 3.6 [1].
Н 
270 T3  K H (u 2  1) 3 270 314  10 3  1,15(3  1) 3

 400.7 МПа   Н   410 МПа
аw
140
b4  u 22
60  3 2
Условие прочности выполнено
2.3.13 Силы, действующие в зацеплении.
В зацеплении действуют три силы:
- Окружная
Ft 
2T2 2  115  10 3

 3286 Н
d3
70
- Радиальная
Fr  Ft
tg
tg 20
 3286
 1227 Н
cos 
0,975
- Осевая
Fa = Ft * tg β=3286*0.228=749 Н
Лист
Изм. Лист
№ докум.
Подпись Дата
1.040.00 00.ПЗ
13
2.3.14 Проверка зубьев на выносливость по напряжениям изгиба
Коэффициент нагрузки КF = KFβ * KFν ( см. стр. 42 [1])
По таблице 3.7 [1] при ψbd = 0,93, твердости НВ ‹ 350 и несимметричном расположении зубчатых колес относительно опор коэффициент КFβ = 1.2.
По таблице 3.8 [1] для косозубых колес 8-й степени точности и скорости 1,05
м/с коэффициент КFυ = 1,1.
Таким образом, КF = 1,2 * 1,1 = 1,32.
Коэффициент, учитывающий форму зуба, YF зависит от эквивалентного
числа зубьев zυ
z3
39

 42
3
cos  0.9753
z4
117
z 

 126
3
cos  0.9753
- У шестерни z 
- У колеса
Коэффициент YF1 = 3,62 и YF2 = 3,6 (см. стр. 42 [1] ).
Определяем коэффициенты Yβ и КFα .
К F

12,83
 0,91
140
140
4  (   1)( n  5) 4  (1.5  1)(8  5)


 0.92 ,
4 
4  1.5
Y  1 
 1
где средние значения коэффициента торцевого перекрытия ε α = 1,5; тепень
точности n = 8.
Допускаемые напряжение при проверке на изгиб определяют по формуле
3.24 [1]:
 0F lim b
,
 F  
S F 
По таблице 3.9 для стали 45 улучшенной предел выносливости при отнулевом цикле изгиба  0F lim b = 1,8 НВ.
Для шестерни  0F lim b = 1,8 * 230 = 414 МПа
Для колеса
 0F lim b = 1,8 * 200 = 360 МПа
Коэффициент безопасности S F   S F ' * S F "
По таблице 3.9 [1] [SF]’ = 1.75 для стали 45 улучшенной; [SF]” = 1 для
поковок и штамповок.
S F   S F '  S F "  1,75 1  1,75
Допускаемые напряжения:
Для шестерни
 F  
 F0
Для колеса
 F  
 F0
limb

414
 236.6 МПа
1,75
limb

360
 205.7 МПа
1,75
S F 
S F 
Лист
Изм. Лист
№ докум.
Подпись Дата
1.040.00 00.ПЗ
14
Проверку на изгиб следует проводить для того зубчатого колеса, для
 
которого отношение F меньше. Найдем отношения:
YF
Для шестерни
Для колеса
236.6
 65.4 МПа
3.62
205.7
 57 МПа
3 .6
Проверку на изгиб проводим для колеса
F 
Ft K F YF K F 3286  1,32  3,6  0,91  0,92

124.5МПа  205,7 МПа
b4 mn
60  1.75
Условие прочности выполнено.
Лист
Изм. Лист
№ докум.
Подпись Дата
1.040.00 00.ПЗ
15