стр. 31-34

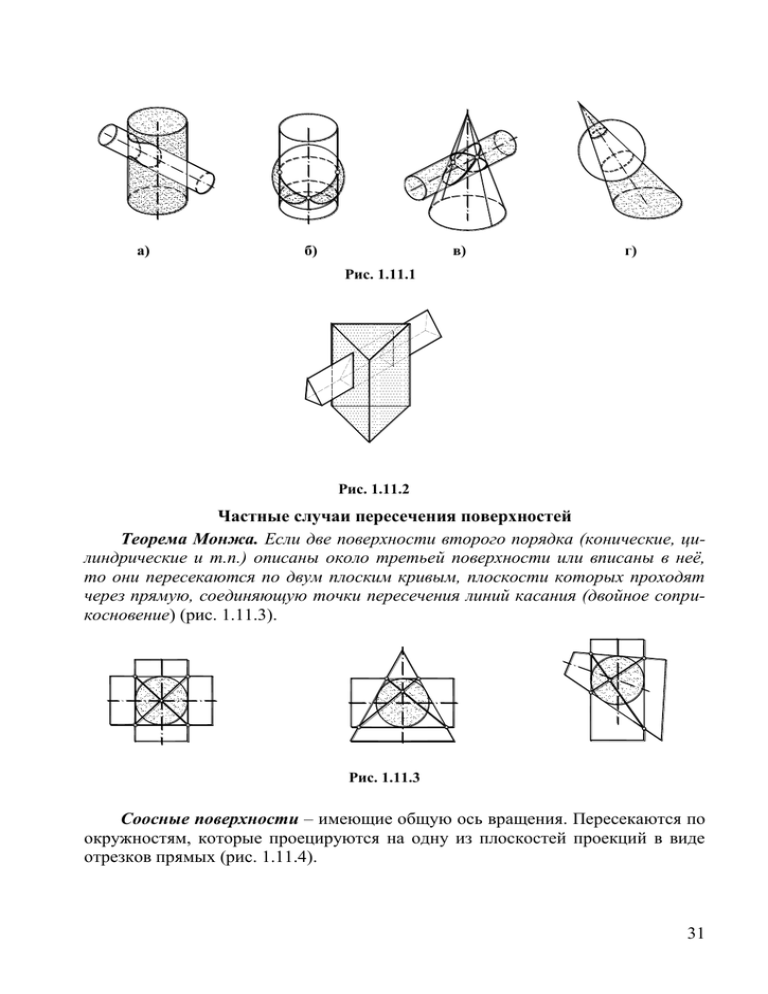
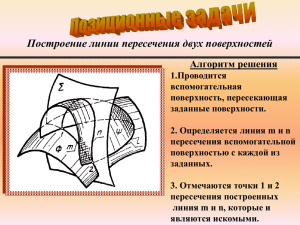
а)
б)
в)
г)
Рис. 1.11.1
Рис. 1.11.2
Частные случаи пересечения поверхностей
Теорема Монжа. Если две поверхности второго порядка (конические, цилиндрические и т.п.) описаны около третьей поверхности или вписаны в неё,
то они пересекаются по двум плоским кривым, плоскости которых проходят
через прямую, соединяющую точки пересечения линий касания (двойное соприкосновение) (рис. 1.11.3).
Рис. 1.11.3
Соосные поверхности – имеющие общую ось вращения. Пересекаются по
окружностям, которые проецируются на одну из плоскостей проекций в виде
отрезков прямых (рис. 1.11.4).
31
Рис. 1.11.4
Построения линии пересечения поверхностей способом вспомогательных
секущих плоскостей
Способ вспомогательных секущих плоскостей – состоит в том, что две
пересекающиеся поверхности пересекаются единой плоскостью уровня. Эта
плоскость в пересечении с поверхностями образует две линии сечения, которые
в пересечении определяют по паре точек, принадлежащих общей линии пересечения поверхностей (рис.1.11.5).
Этот способ применим, когда в результате сечения поверхностей в сечении
получаются простые фигуры (окружности, прямые и т.п.), легко строящиеся с
помощью чертёжных инструментов. Именно поэтому в качестве секущих плоскостей принимаются плоскости уровня (рис. 1.11.6, 1.11.7).
2
2
I2
II2
III
2
IV
2
Рис. 1.11.5
Рис. 1.11.6
Контрольные вопросы:
1. Общие случаи взаимного пересечения поверхностей.
32
 2I
 2II
Рис. 1.11.7
2. Частные случаи взаимного пересечения поверхностей. Теорема Монжа.
3. Алгоритм решения задачи на построение линии пересечения поверхностей
способом вспомогательных секущих плоскостей.
4. Какие точки линии пересечения находятся в начале решения задачи? Какие
точки называют опорными? произвольными?
Решить задачи: 64, 65, 66, 67, 68, 70
Тема 12: «Развертки поверхностей»
Развёртка – плоская фигура, получаемая при совмещении всех точек поверхности с некоторой плоскостью.
Для построения разверток необходимо иметь натуральные величины всех
элементов развертываемой поверхности: её боковых рёбер (или образующих) и
основания (рис. 1.12.1). Если эти элементы занимают о.п., любым из способов
преобразования чертежа необходимо определить их натуральные величины.
Развертка называется полной, когда к развертке её боковой поверхности
добавляются фигуры её основания.
Свойства развёрток: сохраняются длины линий, расположенных на поверхности; величины углов между линиями и площади фигур, ограниченных
замкнутыми линиями.
Поверхности бывают развёртываемые (все многогранные и некоторые
линейчатые) и не развертываемые (все кривые поверхности).
Способ триангуляции
Способ треугольников (триангуляции) – построение развёртки сводится
к многократному построению натуральной величины (Н.В.) треугольников, из
которых состоит поверхность.
S2
н.в. SС
A2
A1
н.в. AB
н.в.
B2
AC
C2
C1
SВ
в. в.
н. н.
i2
S
SA
2
C2
B2
A2
C
B
н.в.AB
B1
C
A
S 1 i1
C1
B1
A
A1
Рис. 1.12.1
33
Приближённые развёртки не развертываемых поверхностей
(на примере сферы).
Заданная поверхность с помощью меридианов разбивается на части, каждую из которых можно приближённо заменить цилиндрической поверхностью
(способ цилиндров) или вписанных конусов (способ вспомогательных конусов)
(рис. 1.12.2).
62 52 72
42 32
12 22
6
4
2
21
7
5
3
1
41 6
1
11
31
51
71
Рис. 1.12.2
Контрольные вопросы:
1. Что называется разверткой поверхности?
2. Какие поверхности называются развертываемыми и какие – не развертываемыми?
3. Какие способы разверток поверхностей вы знаете?
4. Что называется полной разверткой?
5. Укажите основные свойства разверток.
Решить задачи: 71, 72
34