теории прочности.

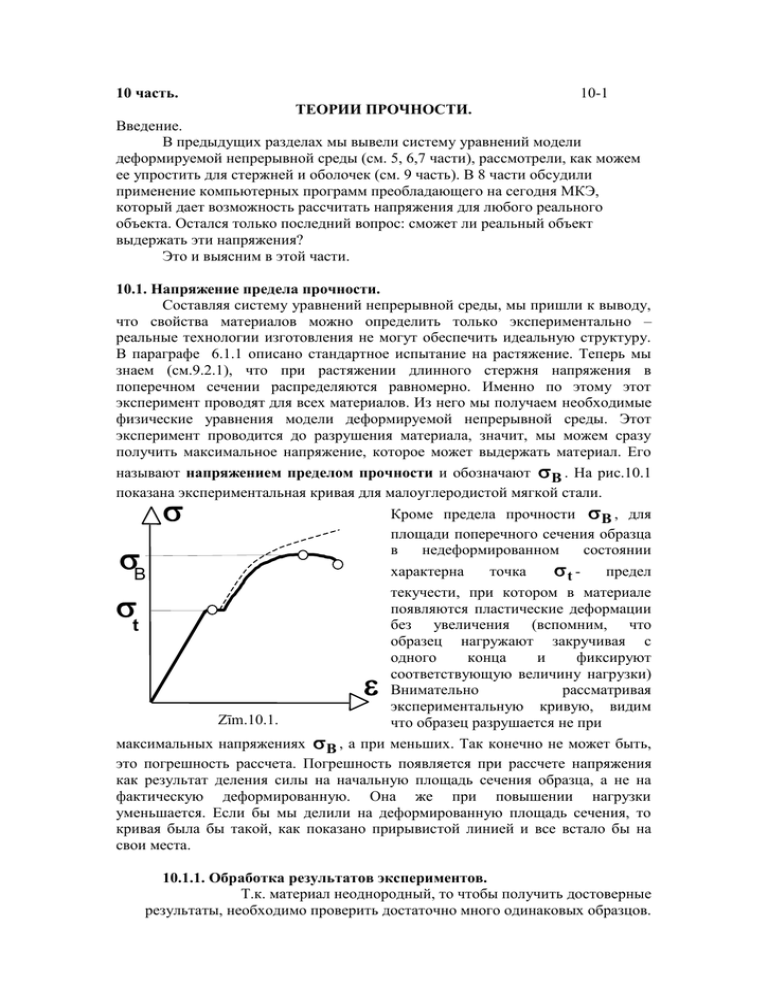
10 часть.
10-1
ТЕОРИИ ПРОЧНОСТИ.
Введение.
В предыдущих разделах мы вывели систему уравнений модели
деформируемой непрерывной среды (см. 5, 6,7 части), рассмотрели, как можем
ее упростить для стержней и оболочек (см. 9 часть). В 8 части обсудили
применение компьютерных программ преобладающего на сегодня МКЭ,
который дает возможность рассчитать напряжения для любого реального
объекта. Остался только последний вопрос: сможет ли реальный объект
выдержать эти напряжения?
Это и выясним в этой части.
10.1. Напряжение предела прочности.
Составляя систему уравнений непрерывной среды, мы пришли к выводу,
что свойства материалов можно определить только экспериментально –
реальные технологии изготовления не могут обеспечить идеальную структуру.
В параграфе 6.1.1 описано стандартное испытание на растяжение. Теперь мы
знаем (см.9.2.1), что при растяжении длинного стержня напряжения в
поперечном сечении распределяются равномерно. Именно по этому этот
эксперимент проводят для всех материалов. Из него мы получаем необходимые
физические уравнения модели деформируемой непрерывной среды. Этот
эксперимент проводится до разрушения материала, значит, мы можем сразу
получить максимальное напряжение, которое может выдержать материал. Его
называют напряжением пределом прочности и обозначают  B . На рис.10.1
показана экспериментальная кривая для малоуглеродистой мягкой стали.
Кроме предела прочности  B , для
площади поперечного сечения образца
в
недеформированном
состоянии
 t - предел
характерна
точка
B
текучести, при котором в материале
появляются пластические деформации
без увеличения (вспомним, что
t
образец нагружают закручивая с
одного
конца
и
фиксируют
соответствующую величину нагрузки)
Внимательно
рассматривая
экспериментальную кривую, видим
Zīm.10.1.
что образец разрушается не при




максимальных напряжениях  B , а при меньших. Так конечно не может быть,
это погрешность рассчета. Погрешность появляется при рассчете напряжения
как результат деления силы на начальную площадь сечения образца, а не на
фактическую деформированную. Она же при повышении нагрузки
уменьшается. Если бы мы делили на деформированную площадь сечения, то
кривая была бы такой, как показано прирывистой линией и все встало бы на
свои места.
10.1.1. Обработка результатов экспериментов.
Т.к. материал неоднородный, то чтобы получить достоверные
результаты, необходимо проверить достаточно много одинаковых образцов.
10-2
Изготовим n образцов из одного и того же материала. Выполним проверку на
растяжение до разрушения, т. е. Получим значения B для всех образцов.
Экспериментально полученный диапазон B (B min  B  B max ) разделим на k
частей. Каждое, находящееся в k-том диапазоне значение B B k  B  Bk+1
(см. рис. 10.2.), наблюдаем в nk эксперименте.
Очевидно
 n k  n.
k 1
Соотношение
nk
n
это вероятность
появления B в k-том диапазоне, т. е.,
вероятность, что образец разрушился
при таком напряжении Bk. Отложим
pk 
вероятность
соответственно
напряжений и
вероятностей.
к-тому
получим
nk
n
диапазону
плотность
( )
Bmin

B

Bmax
Рис.10.2
Теперь можем определить вероятность, с которой стержень разрушится, при
возникающем в конструкции напряжении . Вся площадь под кривой
соответствует случаю, когда все образцы разрушались, т. е. Так как
теоретическая величина напряжения отличается от полученного в
экспериментах на порядок, вероятность разрушения равна одному.
Заштрихованная площадь от Bmin до  является вероятностью (количество
образцов из всех n)  ( ) , что стержень разрушится , если дать нагрузку,
которая соответствует напряжению , т.е. все nk для всех k , которые меньше
выбранного , и поделив на все количество образцов n, определим вероятность
разрушения элемента конструкции, если на него действует напряжение :
k n
k
(  )  
k 1 n
В справочниках дается полученное среднее значение предела прочности
в серии экспериментов
1 n
 B    Bk
n k 1
и напряжение предела текучести
1 n
 t    tk
n k 1
10.2. Допустимые напряжения.
Конструктору, при определении прочности, надо решать компромиссную
задачу. С одной стороны, надо увеличивать площадь поперечного сечения,
чтобы при данной нагрузке напряжения были по возможности меньшими и
10-3
меньше вероятность, что конструкция разрушится. С другой стороны, уменьшая
площадь поперечного сечения, надо уменьшить вес конструкции и количество
используемого материала. Обычно эту проблему формулируют так: напряжения
должны быть меньше чем допустимые напряжения .

   B
B
kB
t

t
 
kt
Рис. 10.3
Допустимые напряжения получают, используя коэффициент запаса
k t , т.е.,

  B 
kB

  t 
kt
k B или
не может разрушится;
не может быть остаточных деформаций.
Коэффициент запаса kB 1 является числом, характеризующим допустимую
вероятность разрушения. Чем меньше допустимая авария, тем больше должен
быть коэффициент запаса kB. Целому ряду отраслей народного хозяйства для
разных конструкций (особенно в строительстве) коэффициенты запаса являются
нормированными, тогда можно сразу принять несколько значений .
10.3. Необходимость теорий прочности.
Если в рассматриваемой точке сечения проверяемого стержня (балки)
напряжения действуют только в одном направлении, тогда для проверки
прочности используют условие (см.рис. 10.4).
  
Если в элементе конструкции вместо напряжений растяжения есть напряжения
сдвига (см. раздел 6.1.2), тогда следует провести эксперимент для сдвига, но ход
мыслей первых двух параграфов остается неизменным.
10-4
На практике состояние в определении напряжений намного сложнее. Так
например в показанном на рис. 10.5 резервуаре (паровом котле), внутри
которого есть давление в двух перпендикулярных направлениях действуют два
разных напряжения 1 и 2. т. е., положение напряжений в любой точке такое,
как показано на рис. 10.5
y

B
 
kB
A
P
B
B
x
A
1

Рис. 10.4
2
1 ,  2   ???
Рис. 10.5
Надо решить такой вопрос: как оценить прочность, если в точке действуют
напряжения в разных направлениях? Есть две возможности. Во-первых, каждой
комбинации напряжений экспериментально определить границу устойчивости,
доведя элемент конструкции до разрушения. Во-вторых, искать такой критерий,
который:
a) в любом положении напряжения можно выразить одной цифрой ;
b) и численные значения которого одинаковы как при разрушении при
одностороннем напряжении (проверка на растяжение), так и при разных
комбинациях напряжений.
Экспериментальный вариант не является реальным. Чтобы хоть сколько
охватить возможные комбинации напряжений, один материал следует
проверять примерно 103 раз. Но только количество марок стали выражается
числом порядка 104. Ясно, что выполнить столько проверок и поместить их в
таблицы для практического использования не реально.
Остается только второй вариант, т. е. надо искать механические
характеристики разрушения. Надо заметить, что невозможно найти одну такую
характеристику, которая подходила бы всем материалам и всем нагрузкам.
Поэтому существуют несколько теорий прочности. У каждой из них есть своя
характеристика.
10-5
10.4 Схема использования теорий прочности.
В основе каждой теории прочности лежит утверждение, что материал
разрушается в той точке, где R- критерий прочности достигает
экспериментально определенного критического значения.
Схема применения теорий прочности следующая:

 ii
R (  )  R (  ij )

 ij
e

e

Рис. 10.6
1. Основываясь на выбранную теорию прочности, вычисляем для каждого
случая нагружения значение соответствующго критерия прочности:
R  R( ij ) , где  ij тензор напряжений с 9 компонентами  ij
В общем случае в каждой из трех перпендикулярных плоскостей нормальное
напряжение ii и два напряжения сдвига ij.
2. Вычисляем величину той же характеристики R (e) в случае стандартной
проверки (растяжения).
3. В соответствии с теорией прочности в одинаково опасном положении
материал находится тогда, если значения R одинаковы как в сложной, так и в
односторонней нагрузке (проверке на растяжение). Значит, зная значение R для
какого-то положения напряжения, мы знаем, что материал нагружен также, как
при растяжении с напряжением e, что соответствует тому же значению R i ( в
диаграмме  -  точку со значением напряжения e определяет это значение R).
Основываясь на это, можем написать, что
R (e) = R (ij).
4.Найдя решение этого уравнения, находим эквивалентное значение
напряжения e, т. е.
e = f(ij),
5.При растяжении образец не может выдержать напряжения большие, чем B,
т.е. eB.
10-6
Условие прочности для растяжения мы получили, введя понятия коэффициента
запаса k и допустимого напряжения . Используя теорию прочности,
конструкцию можно считать безопасной, если
 e  f (  ij )   
10.5 Элементарные теории прочности.
Исторически теории прочности развивались, переходя от простых к
сложным механическим характеристикам R. Сначала приняли (первая теория
прочности), что материал разрушается тогда, когда большие нормальные
напряжения (растяжения) достигают критической величины. Это означает, что
для сложного состояния напряжения надо искать такое сечение (независимо от
системы выбора координат), в котором именно нормальные напряжения
являются самыми большими.
Эта теория дает удовлетворительные результаты только при сложных
нагрузках очень хрупких материалов, потому что хрупкие материалы очень
слабо воспринимают напряжения растяжения. Для них предел прочности при
растяжении на много ниже, чем при сжатии (у кирпича примерно в 10 раз).
Хрупкие материалы разрушаются именно по тому сечению, в котором
наибольшие напряжения растяжения. Для других материалов эта теория себя не
оправдывает. По этой теории, например, для резервуара (см. рис. 10.5) надо
брать большее напряжение 1, а второе напряжение 2 не влияет на прочность.
Основываясь на представлениях физики об строении вещества, можно
предположить, что материал разрушается, когда атомы его кристаллической
решетки отдаляются друг от друга на критическое расстояние. По этой теории
надо найти наибольшие деформации, а не напряжения (как в первой теории), т.
е. надо найти направление, в котором наибольшая продольная деформация , и
перпендикулярное ей сечение и будет тем, по которому материал должен
разрушится.
Из-за поперечных деформаций (например резервуара) на значение
продольной деформации t будут влиять все напряжения. Все-таки эту теорию
нельзя использовать на практике, потому что она сильно отличается от
результатов экспериментов. Это объясняется тем, что материалы,
изготовленные по промышленным технологиям, содержат дислокации, имеют
не идеальную кристаллическую решетку и т. д. Именно это является слабыми
местами материалов. Когда удастся изготовить практически чистые материалы
(в будущем с помощью космических технологий), возможно придется
пересмотреть вопросы связанные полезностью второй (максимальных
деформаций) теории.
10-7
10.5.1. Теория наибольших напряжений сдвига (третья теория).
Materiāls plīst tajā punktā, tajā šķēlumā kurā darbojas lielākie bīdes spriegumi
R   max
Разрушая пластический материал, например, при растяжении,
наблюдается, что на месте, где образец разрушается (в растянутом стержне на
месте горлышка), появляется характерный угол сдвига 450 по отношению к оси
стержня, т. е. материал разрушается,
сдвигаясь по плоскостям, в которых
напряжения сдвига наибольшие.
Схематически удлинение и в
a
последствии разрушение показаны на
рис. 10.7.
o
45




a



S
Рис. 10.7
Рис.10.8
Наибольшие значения напряжения сдвига находим из рис. 10.8, на котором
показан элемент треугольника a растянутого стержня, изображенного на рис.
10.7. При написании условий равновесия оси координат можем выбирать
произвольно. Напишем сумму всех проекций сил на ось . Сила S (Sплощадь косого сечения элемента треугольника (см. рис. 7.6)) дает проекцию
S, а чтобы получить силу, соответствующую напряжению  умноженного на
проекцию площади Scos, которое умножая на sin, получим его проекцию.
Уравнение всех проекций имеет вид:
S -  S cos sin =0
Отсюда
=0,5  sin2
Видно, что  максимально      тогда, когда  = 450. Значит для этой
теории
R 3 ( e )    0,5 e
Приравнивая соответствующее напряжение
R 3 ( e )  0,5 e
этого
эксперимента с соответствующим максимальным напряжением сдвига R(  ij ),
напряженного состояния элемента конструкции, получим уравнение, которое
связывает  e с напряжениями в конструкции. Заменяя  e на  получаем
условие прочности.
 
10-8
Эта теория дает хорошие результаты (хорошо совпадает с
экспериментами на конструкциях с разными напряженными состояниями) для
таких материалов, у которых ярко выражен предел текучести (мягкое железо,
цветные металлы и часть композитных материалов).
10.5.2 Теория прочности по удельной потенциальной энергии
формоизменения.
Материал разрушается в той точке, в которой в процессе
деформации
накоплена
наибольшая
потенциальная
энергия
формоизменения.
Работу, затраченную на растяжение образца находим как произведение силы и
перемещения. Чтобы найти удельную работу a, вырежем из растягиваемого
образца единичный объем 1 x 1 x 1. Сила F тогда S=  (1x1) и перемещение 
= x 1 и удельная находится как


a=  F(  )d =  (  )d
o
o




yz
yy
yx

xy
zy
zz
1
a= 2  
zx
xz
xx

a    ij ij
i j
Естественно принимать за характеристику состояния материала то
количество работы, которое потрачено на деформацию одного кубического
сантиметра. Но существует эксперимент, который не соответствует этому
утверждению. Известно, что на дне океана (давление равно произведению
удельного веса воды на глубину, значит на земном шаре на глубине 10 км
давление равно 1000 Н/см2) не разрушаются даже остатки корабля, а в
лаборатории образцы многих металлов не выдерживают аналогичных
односторонних напряжений растягивания. Количество потраченной энергии
как критерий прочности надо поправлять, принимая, что давление которое не
изменяет форму, а только объем, не влияет на прочность, а “виновата” только
энергия изменения формы.
10-9


l
U  U tilp .m.  Uform .m.
R  a form .m .
U form .m .

V
10.6 Сравнение теорий прочности.
Сравним полученные результаты различных теорий прочности
(см.таб.10.1) дла одного конкретного примера – кручения круглого стержня.
Хрупкий материал разрушается там, где возникают наибольшие
растягивающие напряжения. В случае кручения это угол 450 градусов от оси.
Поэтому вал из чугуна или сильно закаленной стали разрушится под углом 450
(см. преревистую линию рис. таб. 1).
Мягкая сталь – пластичный материал и для него хорошо подходит теория
прочности максимальных сдвиговых напряжений. Наибольшие сдвиговые
напряжения возникают в перпендикулярном сечении, там и происходит
разрушение (см. преревистую линию рис. таб. 1) стержней из мягкой стали или
цветных металлов при кручении.
Сравнивая третью и четвертую теории прочности, видим что
 e 3  2 , а
в третьей теории
в четвертой  e4  3  .
Отличие не более чем на 10%. Очевидно, не имеет смысла проводить расчеты
напряжений с большой точностью, если есть возможность оценить прочность в
этих пределах.

10-10
R   max
Хрупкие мкатериалы


Бетон
Чугун
e  
R   max
Пластичные материалы

e

R  a изм.фор м.

 e  2
a

?
e  3 
Вопросы для проверки
1). Как определить предел прочности материала?
2). Как найти вероятность разрушения материала?
3). Что такое допускаемое напряжение?
4). Что такое коэф. запаса и от чего зависит его значение?
5). Для чего нужны теории прочности?
6). Поясните, какова идея использования теорий прочности.
7). Нарисуйте схематично, как применяются теории прочности.
8). Какие теории прочности Вы знаете?
9). Поясните, как надо применять теорию прочности мах. напряжений сдвига.
10). Какова сущность теории прочности мах. удельной энергии
формоизменения?
11). Поясните, как надо применять теорию прочности мах. удельной энергии
формоизменения?
12). Почему используют разные теории прочности?