Seminary-rekomenduemoe_soderzhanie

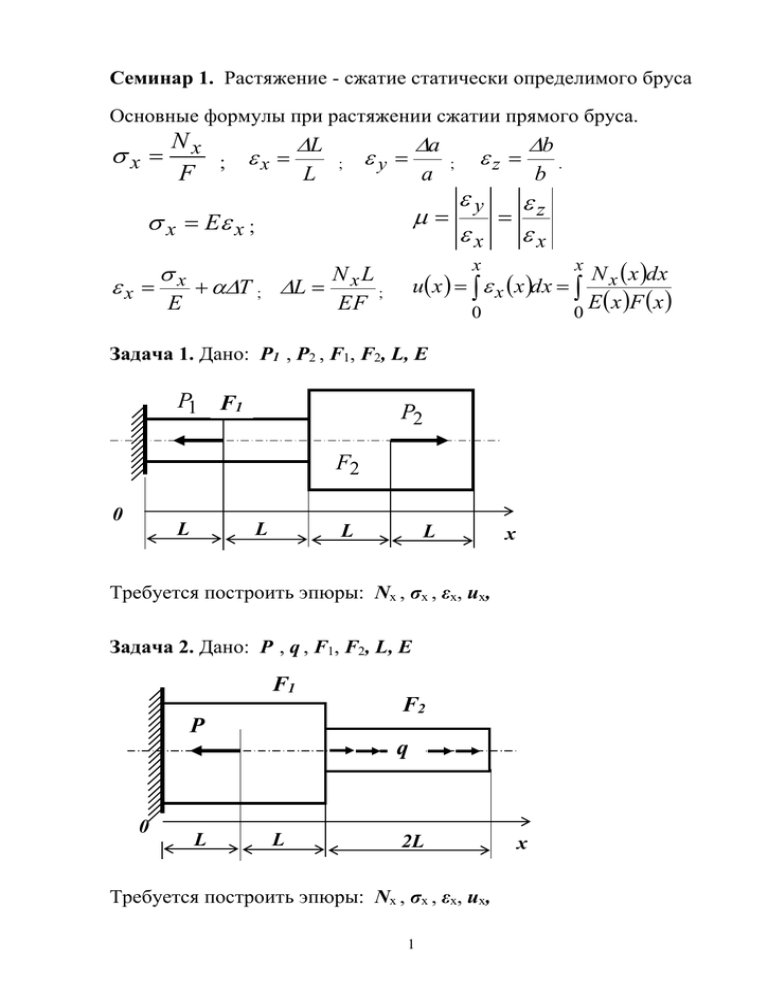
Семинар 1. Растяжение - сжатие статически определимого бруса
Основные формулы при растяжении сжатии прямого бруса.
x 
Nx
L
; x 
F
L
;
y 
x 
E
a

 x  E x ;
x
a
 T ;
;
b
z 
y
x
b

 z
x
N x x dx
E x F x 
0
x
N L
L  x ;
EF
x
ux     x x dx  
0
Задача 1. Дано: P1 , P2 , F1, F2, L, Е
P1 F1
P2
F2
0
L
L
L
L
х
Требуется построить эпюры: Nx , σх , εх, ux,
Задача 2. Дано: P , q , F1, F2, L, Е
F1
F2
P
q
0
L
L
.
2L
Требуется построить эпюры: Nx , σх , εх, ux,
1
х
Семинар 2. Растяжение-сжатие статически неопределимого бруса
Задача 3. Дано: P1 , P2 , F1, F2, L, Е
P1 F1
P2
F2
0
L
L
L
L
х
Требуется построить эпюры: Nx , σх , εх, ux,
Задача 4. Дано: P , q , F1, F2, L, Е, α , ΔT
F1
F2
P
q
ΔT
х
0
L
L
2L
Требуется построить эпюры: Nx , σх , εх, ux,
2
Семинар 3. Стержневые системы.
Задача 5 . Дано: P , F, , L, β, Е
L
А
β
P
Требуется определить продольные усилия и нормальные
напряжения в стержнях, а также перемещение узла А
Задача 6. Дано P , F, , L, β, Е, α, ΔT
ΔT
2F
F

F

Р
L
0,5L
Р
Требуется записать систему уравнений для определения
продольных усилий в стержнях.
3
Задача 7. Дано P , F, , L, а, Е, α, ΔT
F
а
F
а
а
ΔT
L
Р
L
2F
Требуется записать систему уравнений для определения
продольных усилий в стержнях.
Задача 8. Дано P , F, , L, а, δ, β, Е, α, ΔT
ΔT
2F
а
δ
F
L
β
а
а
Р
L
F
Требуется записать систему уравнений для определения
продольных усилий в стержнях.
4
Семинар 4. Анализ плоского напряженного состояния
t
n
 nt
x
n

Fx
Fn
Fy
y
n 
 x  y
2

 x  y
2
cos2 
 nt  
 x  y
t
 nt
x

Fn
 xy
 x  y
 nt  
2

 x  y
2
n
Fx
 xy
n 
n
 x  y
2
y
Fy
cos2    xy sin 2 
sin 2    xy cos2 
5
2
sin 2 
 max

x
 xy
 xy
 max min
tan2  
y

 x  y 

2
 x  y 
2

   xy
 
2

2
2 xy
 x  y
 nt
2
R
 n90
 min
n
 max
n
 max
A
 nt

  min
A  max
2
 max   min   n   n90

  min
R  max
2
6
Задача 9 . Дано: x, 
/2
t
m
x
n
x

Требуется найти значения n , m и nt
Задача 10 . Дано: 1 , 2, , 3,  : 3 = -1 , 2 = 0,  =/2
y
t
1
n

 nt
3 х
z
Требуется найти значения n и nt
7
Чистый
сдвиг
Задача 11 . Дано: 1 , 2, , 3, 
y
t
2
n

1
 nt
х
z
3
Требуется найти значения n и nt
Задача 12 . Дано: x , y , z, xy
Требуется найти значения 1 , 2, , 3 и угол  между 1 и
осью х. Построить круги Мора.
8
Семинар 5. Анализ напряженно-деформированного состояния
Основные уравнения упругости
Связь между напряжениями и деформациями при одноосном
растяжении

x  x
E

 y   z   x   x
E
Связь между напряжениями и деформациями при
чистом сдвиге
 xy 
 xy
G
Закон Гука для трехосного напряженного состояния
1
1    2   3 
E
1
 2   2    3   1 
E
1
 3   3   1   2 
E
1 
Обобщенный закон Гука
x
y
z



 ;
;
1
  x    y  z
E
1
  y    z   x 
E
1
  z    x  y
E



9
;
 xy 
 xy
;
G

 xz  xz ;
G
 yz 
 yz
G
.
Относительное изменение объема
V   x   y   z
V 


1  2
1  2
1   2   3 
 x  y  z 
E
E
Удельная потенциальная энергия деформации
Удельная потенциальная энергия при одноосном напряженном
состоянии
 x2 E x2
1
a   x x 

2
2E
2
Удельная потенциальная энергия при чистом сдвиге
a xy 
 xy xy
2

2
 xy
2G

2
G xy
2
Удельная потенциальная энергия при трехосном напряженном
состоянии

1
 x x   y y   z  z   xy xy   xz xz   yz  yz
2
1 2
a123 
1   22   32  2 1 2  1 3   2 3 
2E
a xyz 


Удельная потенциальная энергия изменения объема и удельная
потенциальная энергия изменения формы
a  a0  aф
1  2
1   2   3 2
6E
1 
1   2 2  1   3 2   2   3 2
aф 
6E
a0 

10


Связь между константами упругости Е , G и 
E
G
21   
Задача 13 . Дано: P , а, h ,  , Е
Требуется найти напряжения на гранях прямоугольного элемента и
относительные деформации элемента в направлении координатных
осей при условии, что в результате действия сжимающей силы P
высота элемента h сравняется с глубиной паза а .
Задача 14 . Дано: x , y , xy , а и 
Требуется найти удлинение диагонали d прямоугольного элемента.
11
Задача 15 . Дано P , а,  ,  , Е
y
P y
a
x
x
z
a
z
a

Требуется найти напряжения на гранях прямоугольного элемента и
относительные деформации элемента в направлении координатных
осей при условии, что в результате действия сжимающей силы P
зазор  между гранью элемента и гранью паза будет
ликвидирован.
12
Семинар 6. Кручение
Основные формулы.
 xt  
Из геометрии деформации следует, что

Относительный угол закручивания
Закона Гука для сдвига
 xt  G xt
С учетом закона Гука
 xt  G
d
dx
d
dx
 xt  
.
Суммарный крутящий момент
M x    xt dF   G 2dF  GI p
F
где
Ip
,
F
- полярный момент инерции сечения, равный
I p    2 dF
F
Зависимость угла закручивания от внешних крутящих моментов
d M x


dx GI p
\
GI p - жесткость сечения при кручении.
Угол закручивания вала длиной L
L
M x dx
GI p
0

Для постоянных по длине бруса значений M x , G и I p

M xL
GI p
13
.
Касательные напряжений при кручении круглого вала как
функция крутящего момента и расстояния от оси вала до
выбранной точки сечения вала
 xt 
Mx

Ip
max
 xt

.
Mx
M
R x
Ip
Wp
W p - полярный момент сопротивления кручению
Ip
Wp 
.
R
Задача 16 . Дано: Значение m и координаты сечений действия
крутящих моментов х1 , х2 , х3 и х4, а также модуль сдвига G
и допускаемое напряжение [ ] и предельный относительный угол
закручивания [ ].
m
0
x1
4m
2m
x2
x3
m
x4
x
Требуется построить эпюры крутящих моментов Mx(x) , углов
закручивания (x) и вычислить диаметр вала D,
удовлетворяющий условиям прочности и жесткости.
14
Задача 17 . Дано: Диаметр вала d , размер a , модуль сдвига G
и допускаемое напряжение [ ].
Требуется вычислить опорные реакции R1 и R2 , построить
эпюры крутящих моментов Mx(x) , максимальных напряжений
(х) , углов закручивания
(x)
и определить предельное
значение крутящего момента М из условия прочности.
15
Семинар 7. Изгиб
Чистый изгиб
Из геометрии деформации следует, что относительная деформация x
выделенного волокна будет равна
dx  yd ;
x 
x  d ;
x  dx  x dx y


x
x 
В соответствии с законом Гука для одноосного растяжения
x 
 x  E x
E

y
MZ , создаваемый напряжениями σx, равен
Изгибающий момент
M z    x ydF 
F
E
2
 y dF 
F
E

Iz ,
где
I z   y 2 dF
F
Для напряжений имеем
x 
E

y
Mz
y,
Iz
и, с учетом закона Гука получаем для относительных деформаций
x 
Mz
y,
EI z
где EIZ – жесткость сечения балки при изгибе.
16
Поперечный изгиб
Формула для касательных напряжений при поперечном изгибе
 xy 
 
Q y S z y*
bI z
,
 
S z y*  F * yc
где
Напряженное состояние при поперечном и чистом изгибе балки
P
P
σX
τXY
–
Z
+
a
Pa
Y
a
x 
MZ
+
 xy 
x
QY
P
Mz
y
Iz
 
Q y S z y*
bI z
bh3
Iz 
12
+
–
-P
17
x
 
2


b
h
 
*
2

Sz y     y

2  2 


Дифференциальные зависимости Журавского
q
dQ у
dx
(1)
dM z
dx
(2)
d 2M z
q
dx 2
(3)
Qy 
Задача 18. Дано: Балка, нагруженная сосредоточенной силой Р
R1
R2
P
a
2a
Требуется определить опорные реакции R1 и R2 и построить
эпюры поперечных сил Qy и изгибающих моментов Mz
Задача 19. Дано: Балка, нагруженная сосредоточенным моментом
М
M
R2
R1
a
2a
Требуется определить опорные реакции R1 и R2 и построить
эпюры поперечных сил Qy и изгибающих моментов Mz
18
Задача 20. Дано: Балка, нагруженная распределенной нагрузкой q
R1
R2
q
a
2a
Требуется определить опорные реакции R1 и R2 и построить
эпюры поперечных сил Qy и изгибающих моментов Mz
Задача 21. Дано: Балка, нагруженная сосредоточенной силой Р,
сосредоточенным моментом М и распределенной нагрузкой q .
R1
M
q
R2
P
a
2a
Требуется определить опорные реакции R1 и R2 и построить
эпюры поперечных сил Qy и изгибающих моментов Mz
19
Задача 22. Дано: Балка, нагруженная сосредоточенной силой Р,
сосредоточенным моментом М и распределенной нагрузкой q .
q = P/a
M = Pa
q
M
a
a
a
Требуется определить опорные реакции и построить эпюры
поперечных сил Qy и изгибающих моментов Mz
Семинар 7а. Продолжение темы «Изгиб»
Задача 23. Стальная балка нагружена сосредоточенной силой Р,
распределенной нагрузкой q и сосредоточенным изгибающим моментом М
q = P/a ;
M = Pa;
2M
q
Р = 10 кН ; а = 1 м.
В
А
а/2
P
2q
a
a
a
Требуется:
1. Определить опорные реакции.
2. Построить эпюры поперечных сил Qy и изгибающих моментов Мz .
3. Подобрать поперечное сечение балки в виде двутавра, приняв
допускаемое значение напряжения равным 160 МПа.
4. Для сечения балки, находящемся на расстоянии а/2 от левой опоры
А, построить эпюры нормальных σx и касательных τxy напряжений.
20
5. Провести анализ напряженного состояния в точке перехода полки
балки в стенку в зоне растяжения на уровне минимальной ширины
поперечного сечения. Результаты анализа (значения и направления
главных напряжений) представить графически.
Задача 24. Опора В балки задачи 22 перемещена в левый конец балки.
q
2M
В
А
а/2
P
2q
a
a
a
Требуется построить эпюры поперечных сил Qy и изгибающих моментов Мz .
Семинар 8.
Перемещения при изгибе.
Дифференциальное уравнение изогнутой оси балки
Сечение балки на расстоянии х от начала координат будет
развернуто на угол θ, причем
dy
   y .
dx
Известно уравнение
M x 
1
 z ,
 x 
EI z
где ρ - радиус кривизны, MZ (x) - эпюра изгибающего
момента, EIZ - жесткость сечения балки при изгибе.
Из курса аналитической геометрии известно, что кривизна кривой равна
21
1

 x 
y 


3
1   y 2 2
Поскольку прогибы малы и первая производная
точностью
у' << 1 , то с большой
1
 y 
 x 
и получаем дифференциальное уравнение изогнутой оси балки
y  
M z x 
EI z .
Интегрируем это уравнение.
Угол поворота сечения будет равен
y    x  
прогиб -
y
1
EI z
1
M z  x dx  c

EI z
,
  M z x dxdx  cx  d
.
Постоянные интегрирования c и d находят из условий, налагаемых
опорами балки на линейные и угловые перемещения.
Теорема Кастилиано
Vn 
U
Pn
или
VОБ 
U
PОБ
(14.13)
Частная производная от потенциальной энергии системы по силе равна
перемещению точки приложения силы вдоль направления действия этой
силы.
22
Интеграл Мора
N X N1 X dx
M X M 1 X dx
U 


 ...



2GI p
 Ф Ф 0 L 2 EF
L
 А  
M Y M 1Y dx
M M dx
  Z 1Z
2 EIY
2 EI Z
L
L

Задача 25. Консольная балка нагружена сосредоточенным изгибающим
моментом М . Известны длина балки L, модуль упругости Е и осевой
момент инерции Iz .
M
x
O
A
L
Требуется вычислить угол поворота конца балки А с использованием
дифференциального уравнения изогнутой оси балки
Задача 26. Консольная балка нагружена сосредоточенным изгибающим
моментом М . Известны длина балки L, модуль упругости Е и осевой
момент инерции Iz .
M
x
O
A
L
Требуется вычислить угол поворота конца балки А с использованием
теоремы Кастилиано.
23
Задача 27. Консольная балка нагружена сосредоточенным изгибающим
моментом М . Известны длина балки L модуль упругости Е
момент инерции Iz .
и
осевой
M
x
O
A
L
Требуется вычислить прогиб конца балки А с использованием теоремы
Кастилиано и метода фиктивной силы..
Задача 28. Балка в виде четверти окружности нагружена сосредоточенной
силой Р . Известны радиус изгиба балки R модуль упругости Е и осевой
момент инерции Iz .
A
Р
R
Требуется вычислить перемещение конца балки А в горизонтальном и
вертикальном направлениях с использованием интеграла Мора.
Семинар 8а. Продолжение темы «Перемещения при изгибе»
Задача 29. Балка нагружена сосредоточенной силой Р, распределенной
нагрузкой q и сосредоточенным изгибающим моментом М .
q = P/a ; M = Pa; Р = 10 кН ; а = 1 м , b = 10 см, h = 20 см,
Е = 2.105 МПа.
24
M
P
q
В
А
h
а/2
2q
a
a
a
ba
Требуется вычислить прогиб сечения балки А и угол поворота сечения В с
использованием интеграла Мора.
Задача 30. Балка нагружена сосредоточенной силой Р, распределенной
нагрузкой q и сосредоточенным изгибающим моментом М .
q = P/a ; M = Pa; Р = 10 кН ; а = 1 м , b = 10 см, h = 20 см,
Е = 2.105 МПа.
M
q
P
В
А
h
2q
a
a
a
b
Требуется вычислить прогиб сечения балки А и угол поворота сечения В с
использованием интеграла Мора.
25
Семинар 9. Сложное сопротивление
Нормальные напряжения
σx= σx(Nx)+ σx(Му)+ σx(Мz)
Для левовинтовой системы координат
x 
Nx M y
M

z  z y ..
F
Iy
Iz
Для правовинтовой системы координат
x 
Nx M y
M

z  z y.
F
Iy
Iz
Уравнение для нейтральной оси имеет вид
Nx M y
M

z z y0
F
Iy
Iz
Касательные напряжения
τxy(Qy)
 x  y,z 
τxz(Qz)
τ
τxt(Mx)
 


   xy Q y    xz Q z    xt M x 
Для круглого вала в расчет принимают только напряжения,
обусловленные крутящим моментом
M 
 
   xt M x   x
Ip
Частные случаи сложного сопротивления
26
Косой изгиб
Задача 31. Поперечное сечение консольной балки – прямоугольный
равнобедренный треугольник.
a
L
P
Требуется вычислить предельную длину балки L, если допускаемое
напряжение [σ] = 100 МПа , а = 5 см, P = 20 кН.
Внецентренное растяжение (сжатие)
Задача 32. Стержень нагружен двумя силами, действующими вдоль нижних
ребер
Требуется найти положение нейтральной оси
в сечении стержня, отстоящем от
конца на расстоянии L при условии, что
Р = 10 кН , h = 5 см, b = 10 см и L = 1 м.
L
h
b
P
2P
Изгиб с кручением
27
Задача 33. Вал круглого сечения нагружен силой Р с помощью
рычага.
y
D
z
x
А
L
L/2
P
Требуется дать анализ напряженного состояния в точке А, если
D = 10 см, L = 1 m, P = 100 кН.
Считая, что допустимое напряжение [] = 150 МПа, проверить прочность
стержня по третьей теории прочности.
Семинар 9а. Продолжение темы «Сложное сопротивление»
Задача 34. Дан пространственный брус круглого поперечного
сечения. q = P/a ; M = Pa; Р = 2 кН ; а = 1 м , Е = 2.105 МПа,
[] = 200 МПа.
2M
a
q
P
a
A
a
2P
D
28
Требуется:
1. Построить эпюры изгибающих и крутящих моментов
2. Найти допустимый диаметр D по третьей теории прочности.
3. Вычислить вертикальное и горизонтальное перемещения
конца бруса А.
Семинар 10. Устойчивость упругих ситем
1740 год. Эйлер, задача об устойчивости сжатого стержня
y
y
y
Pk
h
z
x
L
b
Уравнение упругой линии
y  
EI min y   M z
d2y
2
0
dx
I min  I z
M z   Py
29
Однородное дифференциальное уравнение
EI min y   Py  0
P
k2 
EI min
y  k 2 y  0
Формула Эйлера имеет вид:
Pкр 
 2 EI min
2
L
 кр 
.
Pкр
F
Формула Эйлера с учетом условий закрепления концов стержня:
Lпр  L ;
Pкр
 2 EImin

L 2
Минимальный радиус инерции imin:
I min
2
imin 
Гибкость стержня


F
L
imin
Условие применимости формулы Эйлера
30
 кр
 2 EI min
 2E



  п.ц.
2
2
F
L 

Pкр
 2E
 п.ц.
  пр 
Задача 35. Стальной прямоугольный брус жестко заделан с двух
концов при температуре –20 С0. При какой температуре брус
потеряет устойчивость, если L = 5 м, b = 10 см, h = 20 см,
Е = 2.105 МПа,  = 12,5.10-6 1/С0.
h
L
b
Задача 36. Найти толщину стенки трубы АВ, используемой в
качестве подкоса, если Е = 2.105 МПа, L = 2 м, q = 10 кН/м,
D = 10 см.
q
B
L
A
2L
L
D
31
Задача 37. Стальной стержень длиной L , шириной b и толщиной
h изогнут в виде лука с упругим прогибом  посередине. Концы
изогнутого стержня связаны тетивой.
Е = 2.105 МПа, L = 1 м, b = 25 мм, h = 2,5 мм,  = 5 см.
b
h

Требуется:
1. Найти усилие в тетиве и наибольшее напряжение в изогнутом
стальном стержне.
2. Оценить, как изменится усилие растяжения в тетиве, если
материал стержня заменить на алюминиевый сплав.
32
Семинар 11. Тонкостенные оболочки
Формула Лапласа:
m t q


 m t 
Условие равновесия отсеченной части оболочки:
m 
Px
2rx cos  
Задача 38. Сосуд в виде конуса наполнен жидкостью с удельным
весом  . Известны значения R и H .
R

H
Требуется построить эпюры тангенциальных и меридиональных
напряжений и рассчитать толщину стенки сосуда, используя
третью теорию прочности.
33
Задача 39. Конический сосуд со сферической крышкой полностью
наполнен жидкостью с удельным весом  . Под крышкой создано
давление газа q . Известны значения R и H .
R
q

H
Требуется построить эпюры тангенциальных и меридиональных
напряжений и рассчитать толщину стенки сосуда, используя
третью теорию прочности.
Задача 40. Конические сосуды равной высоты полностью
наполнены жидкостью с удельным весом  . Известны значения R,
r и H .
r
R


H
r
R
Требуется построить эпюры тангенциальных и меридиональных
напряжений.
34
Задача 41. Цилиндрический сосуд с полусферической крышкой и
коническим днищем наполнен жидкостью с удельным весом  ,
над жидкостью создано давление газа q . Известны значения R, h,
z и H .
R
q
z

h
H
Требуется построить эпюры тангенциальных и меридиональных
напряжений и рассчитать толщину стенки сосуда, используя
вторую теорию прочности.
35