Угол между прямыми в пространстве. Теорема о трех перпендикулярах.
реклама
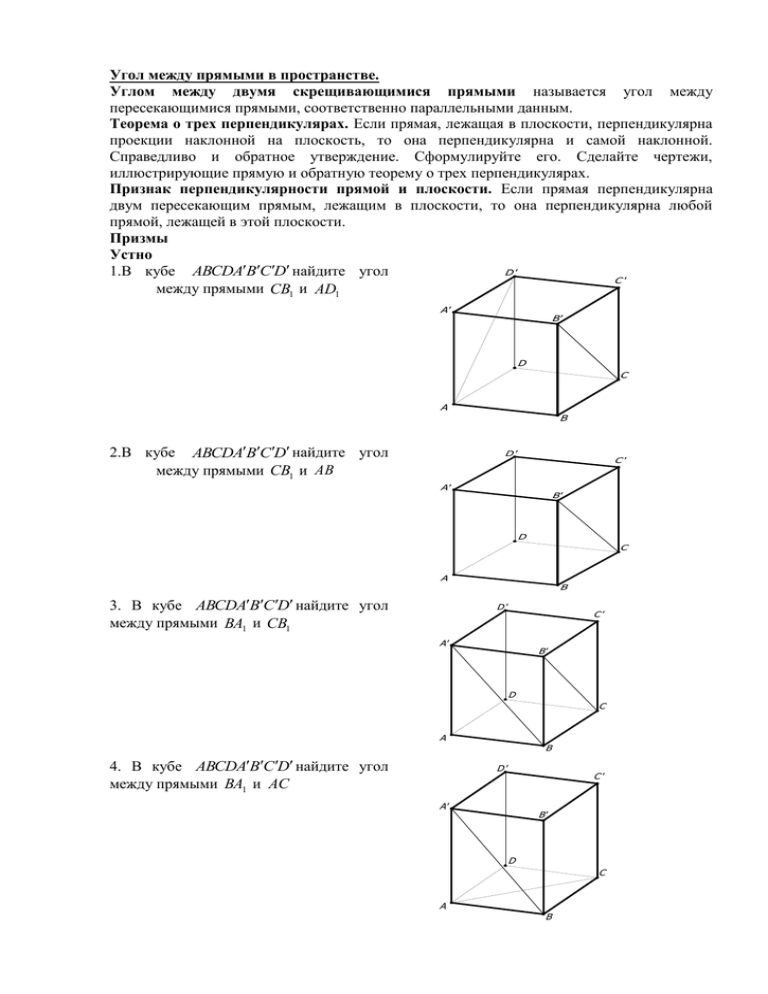
Угол между прямыми в пространстве. Углом между двумя скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным. Теорема о трех перпендикулярах. Если прямая, лежащая в плоскости, перпендикулярна проекции наклонной на плоскость, то она перпендикулярна и самой наклонной. Справедливо и обратное утверждение. Сформулируйте его. Сделайте чертежи, иллюстрирующие прямую и обратную теорему о трех перпендикулярах. Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна двум пересекающим прямым, лежащим в плоскости, то она перпендикулярна любой прямой, лежащей в этой плоскости. Призмы Устно 1.В кубе ABCDABC D найдите угол D' C' между прямыми CB1 и AD1 A' B' D C A 2.В кубе ABCDABC D найдите угол между прямыми CB1 и AB B D' C' A' B' D C A 3. В кубе ABCDABC D найдите угол между прямыми BA1 и CB1 B D' C' A' B' D C A 4. В кубе ABCDABC D найдите угол между прямыми BA1 и AC B D' C' A' B' D C A B 5. В кубе ABCDABC D найдите угол между прямыми DB1 и AC D' C' A' B' D C A B Работа в тетради 1. В кубе ABCDABC D найдите косинус угла между прямыми AB и CA Решение. D' C' Рассматриваем ADC . Почему? В ADC ADC 90 0 , искомый угол A' B' DCA . DC 1 . Объясните, cos DCA AC 3 D C A почему диагональ куба равна 3. B 2.В кубе ABCDABC D найдите тангенс угла между прямыми AB и DB Например, рассмотрим AB D . Он D' C' прямоугольный. Почему? Покажите на чертеже прямой угол. A' Ответ: 2 B' D C A B 3.В кубе ABCDABC D найдите косинус угла между прямыми BD и DB . Решение. Как найти угол между диагоналями Используем теорему косинусов прямоугольника? DOD . 1 D1 B1 Ответ: 3 1 в O B D 2 4.В кубе ABCDABC D точки E и F - середины ребер соответственно A1 B1 и B1C1 . Найдите косинус угла между прямыми AE и BF . D' C' F A' E B' D C A B Решение. D' Почему мы рассматриваем AEF1 ? Искомый угол? Прокомментируйте теорему косинусов в AEF1 : C' F1 A' F E B' 2 2 2 2 5 5 5 5 2 2 2 2 2 2 cos D C 4 5 Ответ: 0,8 cos A B 5.В правильной треугольной призме ABCABC , все ребра которой равны 1, найдите косинус угла между прямыми AB и CB . A' C' B' A C B Решение. Прямая ABAB , значит рассматриваем CBA . A' Объясните, почему СB CA 2 ? C' Искомый угол CBA . 1 B' По теореме косинусов найдите косинус этого угла. 2 2 2 Ответ: 4 A C B 6. В правильной треугольной призме ABCABC , все ребра которой равны 1, найдите косинус угла между прямыми AB и CB . A' C' B' A C B Решение. M A' C' B' A C По построению BC AM Искомый угол B AM , который находим из B AM 1. BA AM 2 Как найти B M ? По теореме косинусов в B AM : Проверьте, что BM 3 B AM : 2. 3 2 2 2 Ответ: B 2 2 2 2 2 cos B AM 1 4 Домашнее задание. 1. В кубе ABCDABC D точки E и F - середины ребер соответственно A1 B1 и C1 D1 . Найдите косинус угла между прямыми AE и BF . D' 5 F C' Ответ: 5 A' E B' D C A B 2. В кубе ABCDABC D точка E - середина ребра A1 B1 . Найдите косинус угла между прямыми AE и BD1 . D' A' C' E B' D C A B Ответ: 15 5 3. EFGHE1 F1G1 H1 - куб. Точки L, N , T - середины ребер F1G1 ; G1 H1 и H1 H соответственно; K - точка пересечения диагоналей грани EE1 F1 F . Заполните таблицу расположения прямых и углов между ними. Прямые Расположение Угол между прямыми 1 LN и EG 2 F1T и FH 3 F1 N и KT 4 TN и EG 5 F1T и KN 6 KH1 и LN Ответ: Прямые Расположение Угол между прямыми 1 скрещиваются 900 LN и EG 2 пересекаются F1T и FH 2 arctg 4 0 3 параллельны 0 F1 N и KT 4 скрещиваются 600 TN и EG 5 пресекаются F1T и KN 5 arccos 5 0 6 скрещиваются 30 KH1 и LN Призма Устно 1.В правильной треугольной призме ABCA1 B1C1 , все ребра которой равны 1, точка D середина ребра BC . Найдите угол между прямыми BB1 и AD . C1 B1 A1 C D B A 2.В правильной треугольной призме ABCA1 B1C1 , все ребра которой равны 1, точка D середина ребра BC . Найдите угол между прямыми A1C1 и AD . C1 B1 A1 C D B A 3.В правильной треугольной призме ABCA1 B1C1 , все ребра которой равны 1, точка D середина ребра BC . Найдите угол между прямыми CB1 и AD . C1 B1 A1 C D B A 4.В правильной шестиугольной призме ABCDEFA1 ...F1 , все ребра которой равны 1, найдите тангенс угла между прямыми AB и CF1 E1 D1 C1 F1 A1 B1 E D C F A B Работа в тетради 1.В правильной треугольной призме ABCA1 B1C1 , все ребра которой равны 1, точки D, E середины ребер соответственно A1 B1 и B1C1 . Найдите косинус угла между прямыми AD и BE C1 E B1 D A1 C B A Решение. C1 Прокомментируйте чертеж. угол? 5 BE AD ; 2 1 1 1 1 2 ED1 2 cos120 0 4 4 2 2 Продолжите решение Ответ: 0,7 D1 E B1 D A1 C B Искомый A 2.В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 , основания которой равны 1, а боковые ребра равны 2, найдите косинус угла между прямыми AB и CD1 E1 D1 1 E1 C1 F1 2 5 B1 E C1 7 F1 A1 D1 A1 D B1 E C F 3 F A D C B B A Решение. Объясните, почему искомый угол Объясните длины отрезков на чертеже. E1 D1C ? Найдите искомый угол. 3. В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 , все ребра которой равны 1, найдите косинус угла между прямыми BA1 и FC1 E1 D1 C1 F1 A1 B1 E D C F B A Решение E1 D1 C1 F1 A1 B1 E D C F С2 B A 10 10 4.В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 , все ребра которой равны 1, точки G и H - середины ребер соответственно A1 B1 и B1C1 . Найдите косинус угла между прямыми AG и BH . A1 BC1C2 ; Искомый угол FC1C2 ; Ответ: E1 D1 H F1 C1 G A1 B1 E D C F A Решение. B E1 D1 C1 H F1 G1 G A1 AGBG1 Искомый угол - HBG1 Примените теорему косинусов в HBG1 Ответ: 0,9 B1 E D C F B A 5.В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 , все ребра которой равны 1, точка G - середина ребра A1 B1 . Найдите косинус угла между прямыми AG и BD1 . E1 D1 C1 F1 G A1 B1 E D C F B A Решение. E1 D1 C1 F1 G B1 A1 E D H Прокомментируйте чертеж. Искомый угол -… 5 13 HD1 , BD1 2, BH . Почему? 2 2 Продолжите вычисления для нахождения искомогоугла. 5 Ответ: 5 C F A B Домашнее задание. 1. В правильной треугольной призме ABCA1 B1C1 , все ребра которой равны 1, точка D середина ребра соответственно A1 B1 . Найдите косинус угла между прямыми AD и BC1 C1 Ответ: B1 D 3 10 20 A1 C B A 2. В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 , все ребра которой равны 1, точка G - середина ребра A1 B1 . Найдите косинус угла между прямыми AG и BD1 . E1 D1 Ответ: C1 F1 10 4 G A1 B1 E D C F A B 3.В кубе ABCDA1 B1C1 D1 точка M - середина B1C1 , точка F - середина D1C1 , точка K середина DC , O - точка пересечения диагоналей квадрата ABCD . Заполните таблицу. Прямые Расположение Угол между прямыми 1 A1 M и BC 2 A1 M и BK 3 C1 K и B1 F 4 C1O и AB1 5 A1 B и B1 D Ответ: Прямые Расположение Угол между прямыми arctg 2 1 Скрещиваются A1 M и BC 2 Скрещиваются 900 A1 M и BK 3 Скрещиваются C1 K и B1 F 2 arcsin 0,4 4 Скрещиваются 300 C1O и AB1 5 Скрещиваются 900 A1 B и B1 D Пирамиды. Устно 1.В правильном тетраэдре ABCD найдите угол между прямыми AB и CD D C A B 2. В правильном тетраэдре ABCD точки E и F - середины ребер соответственно BC и BD . Найдите угол между прямыми AB и EF D E C A F B 3. В правильном тетраэдре ABCD точки E , F и G - середины ребер соответственно BC , BD , AD . Найдите угол EFG D G F C A E B 4.В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1, точки E и F - середины ребер соответственно AB и BC . Найдите угол между прямыми SA и EF . S D C F A E B Работа в тетради 1.В правильном тетраэдре ABCD точка E - середина ребра AD . Найдите косинус угла между прямыми AB и CE . D E C A B Решение. Проведем PEAB , PE - средняя линия ADB . Тогда искомый угол PEC . 3 3 E Объясните, почему PC и CE , 2 2 P 1 а PE . 2 C A Распишите теорему косинусов в EPC . 3 Ответ: B 6 2.В правильной шестиугольной пирамиде SABCDEF , стороны основания которой равны 1, а боковые ребра равны 2, найдите косинус угла между прямыми SA и BD . S Решение. 1.Объясните, почему искомый угол EAS ? 2. Почему EA 3 ? 3.Находим искомый угол, используя теорему косинусов в EAS . D E 3 Ответ: C F 4 D A B 3.В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1, точки E, F - середины ребер соответственно SB и SC . Найдите косинус угла между прямыми AE и BF . S F E D C A B Решение. Прокомментируйте построение искомого угла FBE1 S BF BE1 F E1 C A 5 2 Примените теорему косинусов в FBE1 1 Ответ: 6 FEE1 - прямоугольный: FE1 E D 3 2 B 4. В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1, точки E, F - середины ребер соответственно SC и SD . Найдите косинус угла между прямыми AF и BE . S F E D C A B Решение. Объясните, почему искомый угол KEB ? Как его найти? 5 Ответ: 6 S F E - D C A K B 5.Ребра AD и BC пирамиды DABC равны 24 см и 10 см. Расстояние между серединами ребер BD и AC равно 13 см. Найдите угол между прямыми AD и BC .Ответ: 900 6.Угол между боковыми ребрами правильной четырехугольной пирамиды, не лежащими в 1 одной грани, равен 1200. Найти плоский угол при вершине пирамиды. Ответ: arccos 4 Домашнее задание. 1.В правильной треугольной призме ABCA1 B1C1 , все ребра которой равны 1, точки D, E середины ребер A1 B1 и B1C1 . Найти косинус угла между прямыми AD и BE .Ответ: 0,7 2. В правильной треугольной призме ABCA1 B1C1 , все ребра которой равны 1, точка D 3 10 20 3. В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 , все ребра которой равны 1, найдите косинус угла между прямыми AB1 и BC1 Ответ: 0,75 4. В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 , длина стороны основания равна 3,а длина бокового ребра равна 2. Найдите угол между прямыми A1 F и AD1 . середина ребра A1 B1 . Найти косинус угла между прямыми AD и BC1 .Ответ: 130 52 Подготовка к самостоятельной работе 1. В правильной шестиугольной пирамиде SABCDEF сторона основания AB 3 , а боковое ребро AA1 11. Найдите угол между прямыми SA и BC . Ответ: 300 2. В правильной четырехугольной призме ABCDA1 B1C1 D1 сторона основания AB 4 , а Ответ: arccos боковое ребро AA1 3 . Найдите угол между прямыми AB1 и BC1 . Ответ: 2 arcsin 2 2 5 Самостоятельная работа Вариант 1 В правильной треугольной призме ABCA1 B1C1 , все ребра которой равны 1, найдите косинус угла между прямыми AB и CA1 C1 B1 A1 C B A Вариант 2 В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 , все ребра которой равны 1, найдите косинус угла между прямыми AB и FE1 E1 D1 C1 F1 A1 B1 E D C F B A Вариант 3 В правильной шестиугольной пирамиде SABCDEF , стороны основания которой равны 1, а боковые ребра равны 2, найдите косинус угла между прямыми SB и AD . S D E C F A B Вариант 4 В кубе ABCDA1 B1C1 D1 найдите угол между прямыми A1 B и DB1 D' C' A' B' D C A B Вариант 5 В кубе ABCDA1 B1C1 D1 найдите угол между прямыми A1 B и D1 B1 D' C' A' B' D C A Вариант 6 B В правильной треугольной призме ABCA1 B1C1 , все ребра которой равны 1, найдите косинус угла между прямыми AB1 и BC1 C1 B1 A1 C B A 2 2 1 1 2. 3. 4. 90 5. 60 6. 4 4 4 4 Метод координат Ответы: 1. pq При нахождении угла между прямыми m и l используют формулу cos , где pq векторы p и q параллельны прямым m и l . 1.В единичном кубе ABCDA1 B1C1 D1 найти угол между прямыми AE и DF , где E и F 1 1 точки, расположенные на ребрах CD и C1 D1 так, что DE DC , C1 F C1 D1 . 3 3 D' F A' C' B' D E C A Решение B D' Z A' X C' F B' D E C A B Y 1 1 2 ; D1;0;0 ; E 1; ;0 ; F 1; ;1 ; AE 1; ;0 3 3 3 1 2 2 1 0 0 1 2 3 3 9 cos 2 2 10 13 130 1 2 2 1 12 3 3 3 3 A0;0;0 2 DF 0; ;1 3 2.В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 , ребра которой равны 1, найти угол между прямыми AB1 и BF1 . E1 D1 C1 F1 A1 B1 E D C F B A Решение. Z E1 D1 Y C1 F1 A1 B1 E D C F O A B x 1 1 3 3 ;1 AB1 1;0;1 A ; ;0 , B1 ; 2 2 2 2 3 3 1 3 B ; ;0 , F1 1;0;1 BF1 ; ;1 ; 2 2 2 2 3 1 1 1 2 2 cos 2 8 9 3 2 2 4 2 2 1 4 4 Векторный метод 3. В кубе ABCDA1 B1C1 D1 найти угол между прямыми EF и PQ , где E , F , P, Q - середины ребер DD1 , BC , AA1 и B1C1 соответственно. D' C' A' B' Q E P D C F A B Решение. Введем единичные вектора: D' C' A' B' Q E c P D C a F A b B 1 1 1 1 1 EF c DF c b a a b c 2 2 2 2 2 1 1 1 1 PQ c b a c a b c 2 2 2 2 1 1 1 1 1 EF PQ a 2 b 2 c 2 1 ; cos 4 4 4 4 2 1 2 6 6 2 2 1 4 1 2 6 3