Схема 3 - Reshaem.Net

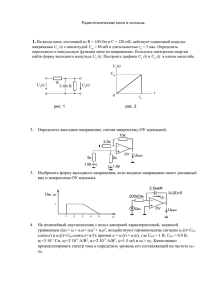
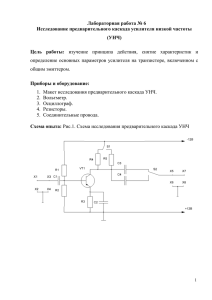
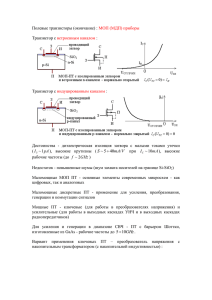
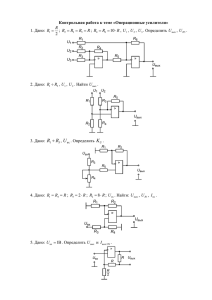
Задание №2. Расчет установившегося синусоидального режима
Постановка задачи
1.
Для заданных двухполюсников "1","2","3" при питании от источника синусоидального
напряжения
определить функции времени мгновенных значений токов в
ветвях, а также показания приборов, измеряющих действующие значения.
2. Для каждой схемы построить векторные диаграммы токов и напряжений, продемонстрировав
выполнение законов Кирхгофа в векторной форме.
3. Определить активные мощности, потребляемые двухполюсниками на заданной частоте.
4. Для схем"1"и"2" получить частотные зависимости модуля комплексного входного
сопротивления
Z вх  
, построить график
Z вх  
в частотном диапазоне 0     .
Схема 3
Рисунок 2.7 - Схема 3
1.
Комплексные сопротивления всех пассивных элементов цепи:
Z C1   j
1
j

  j 500Ом
3
w  C1
2  10  1  10 6
Z C 2  Z C1   j 500Ом
Z C  Z C1   j 500Ом
Z R1  R1  100Ом
Z R 2  R2  100Ом
Z L  w  j  L  0,01  2000  j  j 20Ом
Комплексное сопротивление на участке R1C :
Z R1C  Z R1  Z C  100  j 500  509,9e  j 78, 7 Ом
Комплексное сопротивление на участке R2 L :
Z R 2 L  Z R 2  Z L  100  j 20  101,98e j11,3Ом
Комплексное сопротивление на участке R1CR2 L :
Z R1CR 2 L 

Z R1C  Z R 2 L
509,9e  j 78,7  101,98e j11,3
51999,602e j 78,7 11,3



Z R1C  Z R 2 L 509,9e  j 78,7  101,98e j11,3 101,985cos 78,7  j sin 78,7   cos 11,3  j sin 11,3
51999,602e  j 67, 4
51999,602e  j 67, 4 51999,602e  j 67, 4


 100Ом
101,980,9797  j 4,9  0,98  j 0,196
199,9  480 j
519,99e  j 67, 4
Здесь ошибка в расчете. Синус 78о не равен 4,9. ZL не равно ZC, поэтому в цепи нет параллельного
резонанса и сопротивление не равно 0.
Полное комплексное сопротивление:
Z  Z C1  Z C 2  Z R1CR 2 L   j 500  j 500  100  100  j1000  1005e  j 84,3
Комплексное действующее значение тока:
j0

I  U  113,14e  0,11e j 84,3 A
Z 1005e  j 84,3
Показание амперметра 0,11A .
Находим мгновенное значение тока:
i(t )  0,11 2 sin 2000t  84,3  0,155 sin 2000t  84,3
Находим напряжение на участке R1CR2 L :
U R1CR 2 L  IZ R1CR 2 L  0,11e j 84,3  100  11e j 84,3 В
Находим токи в параллельных ветвях:
j0

I  U  113,14e  0,02e j163 A
1
Z R1C 510e  j 78,7
U
113,14e j 0
I2 

 0,1e j 73 A
j11, 3
Z R2L
102e
Находим мгновенные значения токов параллельных в ветвях:



i1 (t )  0,02 2 sin 2000t  1630  0,028 sin 2000t  1630



i2 (t )  0,1 2 sin 2000t  730  0,14 sin 2000t  730
Напряжения на участках цепи:
U C1  I  Z C1  0,11e j 84,3  500e  j 90  55e  j 5, 7 В
U C1  I  Z C 2  0,11e j 84,3  500e  j 90  55e  j 5, 7 В
U  I  Z  0,02e j163  500e  j 90  10e j 73 В
C
1
C
U R1  I1  Z R1  0,02e j163  100  2e j163 В
U R 2  I2  Z R 2  0,1e j 73  100  10e j 73 В
U  I  Z  0,1e j 73  20e j 90  2e j163 В
L
2.
2
L
Построим векторную диаграмму токов:


м
Рисунок 2.8 - Векторная диаграмма токов к схеме 3
Построим векторную диаграмму напряжений:
Рис.2.9. Векторная диаграмма напряжений к схеме 3
Таким образом, справедлива система уравнений Кирхгофа в комплексной форме:
R1CR2 L
 I  I1  I2

U  U C1  U C 2  U R1  U C
U  U  U  U
C
R2
L
 R1
Активная мощность, потребляемая от источника:
3.
P  I  R1  I 22  R2  0,02  100  0,1  100  0,04  0,1  1,04Вт
2
1
2

2

P  U  I cos   113,4  0,11 0 0  84,30  1,23Вт
Задание 5
1. Для заданной пассивной цепи получить в общем виде передаточную
функцию
К(р)=uвых(р)/uвх(р),
где uвх(р) и uвых(р) – изображения по Лапласу входной uвх(t) и выходной
uвых(t) величин.
Рисунок 5.1 – Схема задания 5
2. По найденной функции К(р) определить переходную h(t) и
импульсную hδ(t) характеристики. Функцию h(t) изобразить на графике.
3. Воспользовавшись формулой интеграла Дюамеля, записать выражения
для функции uвых(t) при импульсном воздействии, заданном графически:
Рисунок 5.1 – Импульсное воздействие для задания 5
Решение:
1. Для заданной пассивной цепи получим в общем виде передаточную
функцию
К(р)=uвых(р)/uвх(р),
где uвх(р) и uвых(р) – изображения по Лапласу входной uвх(t) и выходной
uвых(t) величин.
Рисунок 5.3 – Передаточная функция
U вх (p)
,
1
R
pC
U ( p)
I 2 (p)  вх
,
2R
Uвых (p)  I1 (p)R  I 2 (p)R,
Отсюда передаточная функция
U вх (p)
U ( p)
R  вх
R
1
2R
R
U вых (p) I1 (p)R  I 2 (p)R pC
K ( p) 



U вх (p)
U вх (p)
U вх (p)
I1 ( p ) 

R
1
R
pC
U ( p)
1
 вх
R 
2R
2
1
RC .
1
p
RC
p
2. По найденной функции К(р) определим переходную h(t)
1
p
1
1
1 1
1
1 1
1
1  RC t
1  RC t


RC
h ( t )   K ( p)   
   
.   e
  e
1 p
1 
p 2
2 p
2
2
p
p
RC
RC
и импульсную hδ(t) характеристики.
'
1
1

t 
 1
d
1  RC t
RC 

h  (t)  h(t)     e
   RC e
dt
 2

Импульсная функция
h ( t ) = h( 0 ) ( t ) + h¢( t ) . Добавьте слагаемое.
Функцию h(t) изобразим на графике.
Рисунок 5.4 – График функции h(t)
3. Воспользовавшись формулой интеграла Дюамеля, запишем выражения
для функции uвых(t) при импульсном воздействии, заданном графически:
Рисунок 5.1 – Импульсное воздействие
t
u вых ( t )  u вх (0)  h( t )   u' ()  h( t  )d.
0
Получаем
1
1  t
h ( t )    e RC
2
1
1

t

1
h ( t  )    e RC e RC
2
В первый интервал времени 0≤t<t1:
uвх(0)=0,
u () 
A
A
  u ' () 
t1
t1
t
 1  1 t t A  1  1 t 1 
u вых ( t )  u вх (0)  h ( t )   u ' ()  h ( t  )d  0     e RC        e RC e RC d 
0
 2
 0 t1  2

t

0
1
1
1 t
1
t

A  1  RC t RC  
1 A
A  t
    e
e d     d   e RC  e RC d 
t1  2
2 t1 0
t1
0

1
1

t
t

1 A
A
RC  RC
.
   t  RC  e
e

1


2 t1
t1


Во второй интервал времени t1≤t<2t1:
u2 ( )  A  u2 ' ( )  0
t1
t1
t

 1 RC  tRC

u вых (t )  u вх (0)  h(t )   u1 ' ( )  h(t   )d  A    
(e
 e RC ) 
0
 2 t1

В третий интервал времени 2t1≤t<3t1:
A
A
u 3 ( )     3  A  u 3 ' ( )  
t1
t1
t1
t
0
2 t1
u вых (t )  u вх (0)  h(t )   u1 ' ( )  h(t   )d   u 3 ' ( )  h(t   )d 
t1
t
1
1


t

 1 RC  tRC
 t  A  1
 A    
(e
 e RC           e RC e RC
 2 t1
 2t1 t1   2

d 


t1
t  2 t1
t


 1 RC  tRC
 A
ARC
 A    
(e
 e RC  
(t  2t1 ) 
(1  e RC ) 
t1
 2 t1
 2t1
t t
t

 1
3 RC
t
RC
 A  ( 
 (e RC  e RC 1 ) 

2 t1
2t1
t1
t  2 t1



 1  e RC


.


В четвертый интервал времени 3t1≤t:
t1
3t1
u вых (t )  u в х (0)  h(t )   u1 ' ( )  h(t   )d   u 3 ' ( )  h(t   )d 
0
 1 RC
 A    
(e
 2 t1
t t
 1
RC
e
2 t1
t

RC
1
1

t


 A  1
RC
RC
     e
e
  t   2
 2t1 1  
3t1

d 


t
t  3t
t  2 t1

 1 RC  t t1
 A

ARC RC1
 A 
(e RC  e RC 1  
(3t1  2t1 ) 
(e
 e RC ) 
 2 t
 2t
t1
1
1


t t
t  2 t1
t
 1


 t RC3t1
A
RC
RC


 (e
e
 e
 e RC
RCt 1


.

