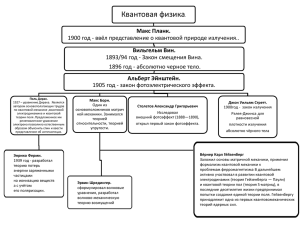
КВАНТОВАЯ ХИМИЯ Проф. Исляйкин Михаил Константинович Квантовая химия – это раздел теоретической химии, в котором строение и свойства химических соединений, их взаимодействия и превращения рассматриваются на основе представлений квантовой механики и экспериментально установленных закономерностей. Цель дисциплины: изучение теоретических основ и применение квантовой химии для описания строения и свойств органических соединений. Задачи дисциплины: o краткое рассмотрение теоретических основ квантовой химии; o ознакомление с квантово-химическими подходами к описанию строения и свойств органических соединений: реакционная способность, ароматичность, таутомерия и др.; o Приобретение практических навыков выполнения квантовохимических расчетов; Трудоемкость дисциплины – 3 зач. ед. Всего часов по дисциплине: Аудиторные занятия: Лекции: Практические занятия: Самостоятельная работа: Форма отчетности 108 час. 51 час. 17 час. 34 час. 57 час. Зач. ГРАФИК выполнения практических занятий Количество баллов № Практическое занятие п/п Контроль 1 Ознакомление с программным комплексом. Оптимизация геометрии и расчет индекса ароматичности. 2 Расчет теплового эффекта органических реакций. Срок проведения II нед. IV нед. 10 3 Расчет электронного распределения. Электрофильное и нуклеофильное замещение. VI нед. 10 4 Расчет переходных состояний и активационных барьеров плоской инверсии. VIII нед. 10 5 Расчет переходных состояний и активационных барьеров таутомерных превращений. Расчет переходных состояний органической реакции. Оценка активационного барьера. Защита реферата Выполнение контрольного задания. Зачет. ИТОГО: X нед. 10 XII нед. 10 XIV XVI нед. XVII нед. 10 10 20 100 6 7 8 10 ЛИТЕРАТУРА Основная: 1. Цирельсон В.Г. Квантовая химия. Молекулы, молекулярные системы и твердые тела: учебное пособие для вузов / В.Г. Цирельсон – М.:БИНОМ. Лаборатория знаний, 2010. – 496 с. : ил. – (Учебник для высшей школы). 2. Исляйкин М.К. Применение квантово-химических методов для описания свойств органических соединений. Методические указания : Иван. гос. хим.технол. ун-т. Иваново 2005. 44 с. (№ 926). ОСНОВНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ МЕХАНИКИ Квантовая механика является дедуктивной наукой, основанной на фундаментальных постулатах. Эти постулаты не очевидны, однако их правильность подтверждается теориями, опирающимися на них и приводящими к результатам, согласующимся с экспериментом. Они являются основой для описания химии на атомном и молекулярном уровнях. Основополагающая роль в становлении и развитии квантовой физики принадлежит М.Планку, Л. де Бройлью, Н.Бору, Э.Шрĕдингеру, П.Дираку и др. Макс Планк Макс Карл Эрнст Людвиг Планк (нем. Max Karl Ernst Ludwig Planck; 1858 — 1947). Выдающийся немецкий физик. Лауреат Нобелевской премии по физике (1918). Как основатель квантовой теории, он предопределил основное направление развития физики с начала XX века. Луи де Бройль Луи Виктор Пьер Раймон, 7-й герцог Брольи (фр. 1892 –1987) — французский физик-теоретик, один из основоположников квантовой механики. Лауреат Нобелевской премии по физике (1929). Нильс Бор Нильс Хе́нрик Дави́д Бор (дат. 1885 – 1962) — датский физик-теоретик и общественный деятель, один из создателей современной физики. Лауреат Нобелевской премии по физике (1922). Н.Бор известен как создатель первой квантовой теории атома и активный участник разработки основ квантовой механики. Э́рвин Шрё́ дингер Э́рвин Ру́дольф Йо́зеф Алекса́ндр Шрё́ дингер (нем. Erwin Rudolf Josef Alexander Schrödinger; 1887 — 1961) — австрийский физик-теоретик, один из создателей квантовой механики. Лауреат Нобелевской премии по физике (1933). Поль Дира́к Поль Адриен Морис Дира́к (фр., 1902 - 1984 — английский физик-теоретик, один из создателей квантовой механики. Лауреат Нобелевской премии по физике 1933 года. Физические законы, составляющие основу математической теории большей части физики и всей химии, таким образом, досконально изучены; трудность заключается лишь в том, что строгое применение этих законов приводит к уравнениям настолько сложным, что их невозможно решить. Поэтому желательно разработать на основе квантовой механики приближенные практические методы, с помощью которых можно было бы без лишних расчетов выяснить особенности систем, состоящих из атомов. Поль Дирак, 1929 год Постулаты квантовой механики Любая система может существовать только в особых состояниях (дискретных или собственных состояниях). Каждое такое состояние характеризуется волновой функцией Ψi. ПОСТУЛАТ 1. Вся информация относительно свойств системы (атома, молекулы, иона, радикала и др.), состоящей из N частиц, заключается в волновой функции Ψ(q, t), которая зависит только от координат (q) N частиц и времени (t). Если время входит в явном виде, то она называется зависящей от времени волновой функцией; если нет, то говорят, что система находится в стационарном состоянии. Волновая функция должна быть однозначной, конечной и непрерывной во всем пространстве переменных и отвечать условиям нормировки: 2 * ∫ Ψ dτ = ∫Ψ Ψdτ = 1 где Ψ*- функция комплексно сопряженная с Ψ. Это выражение означает, что вероятность найти систему во всем пространстве равна 1. ПОСТУЛАТ 2. Каждой динамической переменной (координата, импульс, энергия и т.д.) ставится в соответствии линейный самосопряженный оператор. Все функциональные отношения между величинами классической механики в квантовой механике заменяются отношениями между операторами. Сведения об операторах – закон, в соответствии с которым одной функции f ставится в L̂ соответствие другая функция g: Lˆ f = g L̂ – линейный, если для любых произвольных функций f1 и f2, любых чисел α1 и α2 выполняется соотношение: Lˆ (α 1 f1 + α 2 f2 ) = α 1 Lˆ f1 + α 2 Lˆ f2 L̂ – самосопряженный, если выполняется правило: ∗ * * dτ ˆ ˆ = f L gd τ g L f ∫ ∫ f *и L̂* получаются из f и L̂ заменой знака перед мнимой частью. В квантовой механике различные физические величины заменяются операторами. 1. Оператор координаты x̂ Его действие на любую функцию заключается в умножении ее на х: xˆ f = xf ∧ 2. Оператор импульса PX . Его определяют через операторы проекций: ∧ ∧ ∂ ∂ ∂ P = − i Pz = − i Px = − i y ∂y ∂z ∂x h = , h – постоянная Планка, h = 6.626 x 10-34 Дж/с. 2π ∧ где ∂ ( f ( x )) PX f ( x ) = − i ∂(x) ∧ 3. Оператор кинетической энергии T̂ Классическая механика: 1 mυ 2 p2 ( T= PX2 + PY2 + PZ2 ) = = 2 2m 2m Квантовая механика: 2 2 2 где me масса электрона Введем обозначение: - оператор Лапласа, - оператор набла. Полная энергия в классической механике: E = T +V Оператор полной энергии для атома водорода в квантовой механике: ПОСТУЛАТ 3. Уравнение Шрёдингера для стационарного состояния, т.е. состояния, не зависящего от времени: Ψ(q) – собственная функция оператора Гамильтона Ĥ; E – собственное значение оператора Гамильтона Ĥ. Каждому собственному значению оператора Гамильтона Ei соответствует своя собственная функция Ψi(q). Если одно собственное значение оператора Гамильтона соответствует одновременно нескольким собственным функциям, то такое состояние называется вырожденным с кратностью вырождения m. Например, 3 p-орбитали атома азота имеют одну и ту же энергию, т.е. кратность вырождения данного состояния равна 3 (трижды вырожденное состояние). Функции Ψi и Ψj, относящиеся к различным собственным значениям Ei и Ej, ортогональны, т.е. выполняются соотношения: Условие одновременной ортогональности и нормированности (ортонормированности) функций Ψi (i = 1, 2, …, ∞) записывается следующим образом: где δij – символ Кронекера, определяемый следующим образом: ПОСТУЛАТ 4. Единственно возможными значениями, которые могут быть получены при измерении динамической переменной A, являются собственные значения A операторного уравнения: ПОСТУЛАТ 5. Среднее значение физической величины <A>, имеющей квантово-механический оператор Â, в состоянии Ψ определяется соотношением: Среднее значение полной энергии системы в состоянии Ψ равно Из двух последних постулатов следует, что в квантовой механике физическая величина имеет определенное значение только тогда, когда Ψ, описывающая состояние системы, является собственной функцией оператора, соответствующего данной физической величине. При этом получается ряд дискретных значений собственных чисел. Если Ψ не является собственной, то получается разброс значений этой величины и можно измерить ее среднее значение. Например. Пусть некоторое свойство системы нельзя охарактеризовать собственными функциями, соответствующими данному параметру a, тогда при измерении этого параметра будет получаться не один и тот же результат, а распределение результатов. При этом средняя величина будет определяться выражением: aS = aS = ⟨Ψ S αˆ Ψ S ⟩ ΨSΨS , где ΨS – пробная функция. Иначе, когда ΨS не является собственной функцией оператора α̂ , используя последнее выражение можно получить среднюю величину aS . ПОСТУЛАТ 6. Принцип суперпозиции. Если система может находиться в состояниях, описываемых волновыми функциями Ψ1 и Ψ2, то она может находиться и в состоянии Ψ = c1Ψ1 + c2Ψ 2 где с1 и с2 – коэффициенты, характеризующие вклад Ψ1 и Ψ2 в Ψ. Их находят при условии ортонормированности Ψ1 и Ψ2 из соотношения: c i = ∫Ψ i ∗Ψ i dτ ; ∑ c i2 = 1 Функция Ψ описывает такое состояние, при котором система находится в состоянии Ψ1 с вероятностью (с1)2 либо в состоянии Ψ2 с вероятностью (с2)2. ПОСТУЛАТ 7. Волновая функция Ψ системы частиц с полуцелым спином (в частности, электронов) должна быть ассиметрична относительно перестановки координат любых двух частиц: Соотношение неопределенностей Речь идет о двух группах динамических переменных, характеризующих систему: - координаты и время (пространственные) (q и t); - импульс и энергия (p и E). Причем, невозможно определить одновременно переменные из различных групп с любой степенью точности. Соотношение неопределенностей Гейзенберга: ∆q ⋅ ∆p ≥ 2 ∆t ⋅ ∆E ≥ 2 Вернер Карл Гейзенберг (1901 - 1976) – немецкий физик-теоретик, один из создателей квантовой механики. Лауреат Нобелевской премии по физике (1932). Например: Систему, состоящую из n-степеней свободы можно описать с помощью n значений импульсов и n значений времени. 2n значения динамических переменных могут быть определены с любой нужной степенью точности. Однако прецизионные измерения свойств микрочастиц показали, что точность определения ограничена. С помощью микроскопа определяется положение микрочастиц, неопределенность измерения связана с длиной волны используемого света ∆x = λ . Длина волны может быть малой и тогда координата х должна определяться с любой точностью. Однако использование коротковолнового излучения (света) приведет к заметному изменению импульса наблюдаемой частицы и как следствие к неопределенности его величины: h ∆p = λ В результате неопределенности координата и импульс связаны соотношением: ∆x ⋅ ∆p = h Точность одновременного определения регулируется принципом неопределенности. этих двух величин