Задание 011g -11 по теме «Площадь поверхности и объем прямой призмы»

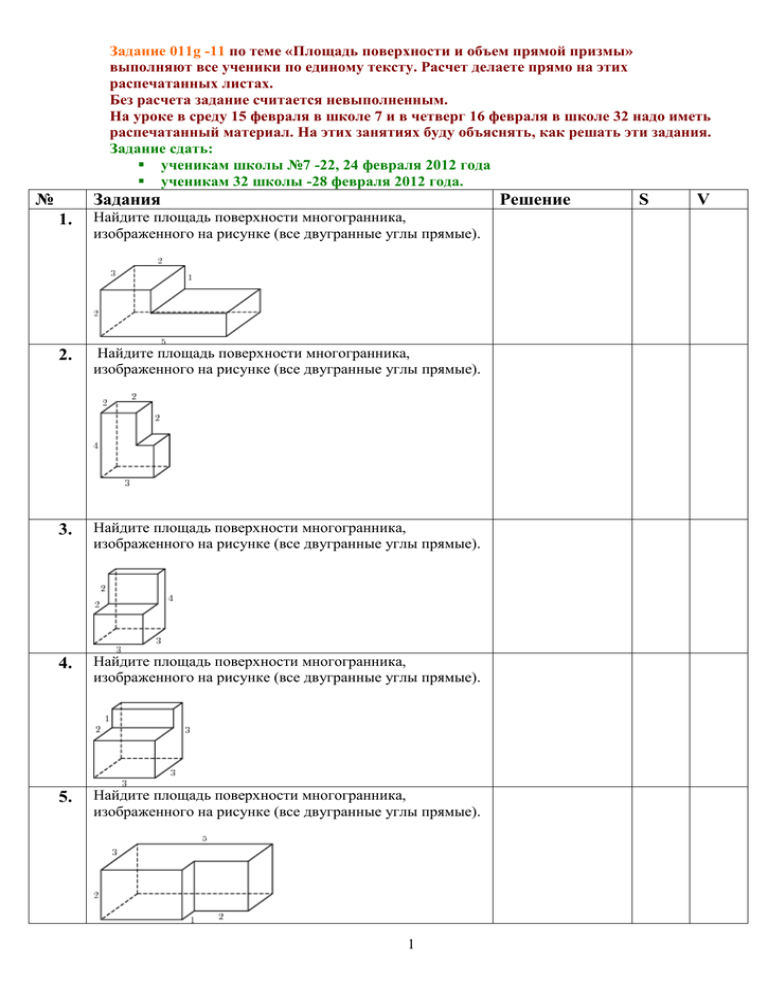
Задание 011g -11 по теме «Площадь поверхности и объем прямой призмы»
выполняют все ученики по единому тексту. Расчет делаете прямо на этих
распечатанных листах.
Без расчета задание считается невыполненным.
На уроке в среду 15 февраля в школе 7 и в четверг 16 февраля в школе 32 надо иметь
распечатанный материал. На этих занятиях буду объяснять, как решать эти задания.
Задание сдать:
 ученикам школы №7 -22, 24 февраля 2012 года
 ученикам 32 школы -28 февраля 2012 года.
№
Задания
Решение
1.
Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
2.
Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
3.
Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
4.
Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
5.
Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
1
S
V
6.
Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
7.
Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
8.
Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
9.
Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
10. Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
11. Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
12. Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
2
13. Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
14. Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
15. Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
16. Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
17. Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
18. Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
19. Найдите площадь поверхности многогранника,
3
изображенного на рисунке (все двугранные углы прямые).
20. Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
21. Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
22. Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
23. Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
24. Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
4
25. Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
26. Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
27. Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
28. Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
29. Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
5
30. Два ребра прямоугольного параллелепипеда, выходящие
из одной вершины, равны 3 и 4. Площадь поверхности
этого параллелепипеда равна 94. Найдите третье ребро,
выходящее из той же вершины.
31. Два ребра прямоугольного параллелепипеда, выходящие
из одной вершины, равны 2 и 6. Площадь поверхности
этого параллелепипеда равна 136. Найдите третье ребро,
выходящее из той же вершины.
32. Площадь поверхности куба равна 18. Найдите его
диагональ.
33. Объем куба равен 8. Найдите площадь его поверхности.
34. Найдите площадь боковой поверхности правильной
шестиугольной призмы, сторона основания которой равна
5, а высота — 10.
35. Найдите площадь боковой поверхности правильной
шестиугольной призмы, сторона основания которой равна
5, а высота — 5.
36. Два ребра прямоугольного параллелепипеда, выходящие
из одной вершины, равны 1, 2. Площадь поверхности
параллелепипеда равна 16. Найдите его диагональ.
6
37. Два ребра прямоугольного параллелепипеда, выходящие
из одной вершины, равны 6 и 12. Площадь поверхности
параллелепипеда равна 576. Найдите его диагональ.
38. Если каждое ребро куба увеличить на 1, то его площадь
поверхности увеличится на 54. Найдите ребро куба.
39. Если каждое ребро куба увеличить на 9, то его площадь
поверхности увеличится на 594. Найдите ребро куба.
40. Если каждое ребро куба увеличить на 2, то его площадь
поверхности увеличится на 192. Найдите ребро куба.
41. Найдите площадь поверхности прямой призмы, в
основании которой лежит ромб с диагоналями, равными 6
и 8, и боковым ребром, равным 10.
42. Найдите площадь поверхности прямой призмы, в
основании которой лежит ромб с диагоналями, равными 9
и 40, и боковым ребром, равным 55.
43. Найдите площадь поверхности прямой призмы, в
основании которой лежит ромб с диагоналями, равными
25 и 60, и боковым ребром, равным 25.
44. Найдите боковое ребро правильной четырехугольной
призмы, если сторона ее основания равна 20, а площадь
поверхности равна 1760.
45. Найдите боковое ребро правильной четырехугольной
призмы, если сторона ее основания равна 15, а площадь
поверхности равна 930.
7
46. Найдите боковое ребро правильной четырехугольной
призмы, если сторона ее основания равна 8, а площадь
поверхности равна 416.
47. Через среднюю линию основания треугольной призмы,
площадь боковой поверхности которой равна 24,
проведена плоскость, параллельная боковому ребру.
Найдите площадь боковой поверхности отсеченной
треугольной призмы.
48. Через среднюю линию основания треугольной призмы,
площадь боковой поверхности которой равна 6, проведена
плоскость, параллельная боковому ребру. Найдите
площадь боковой поверхности отсеченной треугольной
призмы.
49. Из единичного куба вырезана правильная
четырехугольная призма со стороной основания 0,5 и
боковым ребром 1. Найдите площадь поверхности
оставшейся части куба.
50. Из единичного куба вырезана правильная
четырехугольная призма со стороной основания 0,7 и
боковым ребром 1. Найдите площадь поверхности
оставшейся части куба.
8