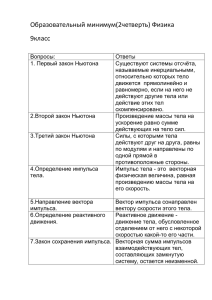
Сила. Второй закон Ньютона. В инерциальных системах отсчета ускорения возникают только под действием других тел на данное тело. Рассмотрим серию экспериментов. ⃗⃗⃗⃗⃗⃗⃗ 𝑉01 = ⃗0⃗ 1) Первоначально покоящаяся тележка имеет пластину, связанную нитью. Тележка не взаимодействует с другими телами (действие Земли и стола скомпенсировано). После пережигания нити тележка покоится → 𝑎⃗ = ⃗0⃗. 0 𝑎 ⃗⃗⃗⃗⃗1 = ⃗0⃗ ⃗⃗⃗⃗1 = 0 ⃗⃗ 𝑉 2) Две первоначально покоящиеся одинаковые тележки связаны нитью: 𝑚1 = 𝑚2 . После пережигания нити, в результате взаимодействия, тела начинают двигаться в противоположные стороны с разными скоростями. В результате взаимодействия первое тело получает 2𝑙 ⃗⃗⃗⃗⃗⃗⃗ 𝑉01 = ⃗⃗ 0 ⃗⃗⃗⃗ 𝑉1 ⃗⃗⃗⃗⃗⃗⃗ 𝑉02 = ⃗⃗ 0 0 𝑎1 ⃗⃗⃗⃗⃗ 𝑎2 ⃗⃗⃗⃗⃗ ⃗⃗⃗⃗ 𝑉2 2𝑙 ускорение 𝑎1 = ∆𝑡12 , втрое тело - 𝑎2 = ∆𝑡22 . 𝑎1 ↑↓ 𝑎2 → ⃗⃗⃗⃗⃗⃗⃗ 𝑉01 = ⃗0⃗ ⃗⃗⃗⃗ 𝑉1 Измеряя ⃗⃗⃗⃗⃗⃗⃗ 𝑉02 = ⃗0⃗ 0 𝑎1 ⃗⃗⃗⃗⃗ l1 𝑎2 ⃗⃗⃗⃗⃗ l2 пути, пройденные тележками 1 и 2, имеем ⃗⃗⃗⃗ 𝑉2 𝑙1 𝑙2 𝑎1 𝑎2 l1 l2 = 𝑚 = 𝑚2 = 1. 1 3) На одну из тележек установим груз: 𝑚1 > 𝑚2 . После пережигания нити тележки проходят разные пути: 𝑙1 < 𝑙2 ⇒ 𝑎1 < 𝑎2 . Но 𝑎1 𝑎2 = 𝑚2 𝑚1 ⇒ 𝑚1 𝑎1 = 𝑚2 𝑎2 или в векторном виде: 𝑚1 ⃗⃗⃗⃗⃗ 𝑎1 = −𝑚2 ⃗⃗⃗⃗⃗ 𝑎2 Интенсивность взаимодействия данных двух тел можно изменять, изменяя расстояние между взаимодействующими телами и их относительные скорости, что приводит к изменению модулей ускорений тел, но последнее равенство будет сохраняться. Следовательно, величина, равная 𝑚1 ⃗⃗⃗⃗⃗ 𝑎1 может являться мерой действия второго тела на первое и называется силой, с которой второе тело действует на первое. Величина, равная 𝑚2 ⃗⃗⃗⃗⃗ 𝑎2 называется силой действия второго тела на первое. Сила – количественная характеристика взаимодействия минимум двух тел, в результате которого тела получают ускорения или деформируются. 𝐹⃗ = 𝑚𝑎⃗ Т.к. m – величина скалярная и положительная, то 𝐹⃗ ↑↑ 𝑎⃗ → произведение массы на ускорение есть новая векторная физическая величина – сила, имеющая такое же направление, как и ускорение, которое она сообщает телу. Си: [F]=> 1Н = 1 1Н кг∙м с2 – сила, которая сообщает телу массой 1кг ускорение 1Н. Сила является причиной изменения скорости (появления ускорения), а не причиной движения тела. Направление скорости движения тела (как и перемещения) может не совпадать с направлением действия силы. Силы обусловлены действиями на данное тело каких-либо других тел. В условиях Земли на каждое тело действуют другие тела. Тела во Вселенной так же взаимодействуют друг с другом. Все тела состоят из молекул, атомов и т.д. – и все эти микротела взаимодействуют. Взаимодействующих тел и элементарных частиц бесчисленное множество; картина взаимодействия тел в природе кажется очень сложной. Однако, по современным представлениям, выделяют 4 типа фундаментальных сил: 1) Гравитационные силы (силы всемирного тяготения): действуют всегда и между всеми телами. Гравитационные силы являются силами притяжения. Например: 𝐹⃗тягот ; 𝐹⃗тяж . 2) Электромагнитные силы: действуют между электрически заряженными частицами, из которых состоят тела. Электромагнитные силы могут быть как силами притяжения, так и силами отталкивания. Например: 𝐹⃗тр ; 𝐹⃗упр ; 𝑃⃗⃗ . 3) 4) Ядерные силы: действуют внутри атомных ядер. Слабые силы: возникают при превращении элементарных частиц. В механике Ньютона рассматривается только два первых типа сил. Все ускорения тел, движение которых подчиняется законам классической механики, объясняются действием на тела или сил всемирного тяготения или электромагнитных сил, или и тех и других одновременно. Любая сила характеризуется: 1) Величиной; 2) Направлением; 3) Точкой приложения. Сила – вектор. Найдем проекции вектора силы на оси. Из прямоугольного треугольника: Y 𝐹 = √𝐹𝑥 2 + 𝐹𝑦 2 𝐹⃗ Fy m α Fx 0 Х 𝐹𝑥 > 0 если 𝐹⃗ ↑↑ ⃗⃗⃗⃗⃗⃗ 𝑂𝑋 ⃗ 𝐹𝑥 < 0 если 𝐹 ↑↓ ⃗⃗⃗⃗⃗⃗ 𝑂𝑋 𝐹𝑥 = 𝐹𝑐𝑜𝑠𝛼 𝐹𝑦 = 𝐹𝑠𝑖𝑛𝛼 Способы измерения силы: ⃗⃗ 𝑁 ⃗⃗ = 𝑐𝑜𝑛𝑠𝑡 ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ 𝑉 1) Для того чтобы измерять силы, необходимо их сравнивать. Две силы, независимо от их природы, считаются равными по 𝐹⃗тяж модулю, но противоположно направленными, если их одновременное ⃗⃗ действие на тело не меняет его скорость (не сообщает телу 𝐹⃗тяж = −𝑁 ускорение). Это утверждение позволяет измерять силы, если одну из них принять за единицу. Такой способ измерения силы называется статический. Он заключается в следующем: неизвестную силу, действующую на тело, уравновешивают известной силой. Модуль измеряемой силы будет равен модулю уравновешивающей ее силы, а направление будет противоположно направлению уравновешивающей силы. Уравновешивающую силу часто измеряют с помощью динамометра, основной частью которого является проградуированная упругая пружина. Известно, что на тело массой 100г действует сила тяжести 𝐹тяж = 𝑚𝑔 = м 0,1кг ∙ 10 с2 = 1Н. Для того чтобы проградуировать пружину, будем сравнивать силу упругости пружины с силой тяжести 𝐹тяж = 𝐹упр . К вертикально расположенной пружине подвешиваются грузы массами 100г и на стенке 𝐹⃗упр динамометра отмечается удлинение пружины в Ньютонах (т.к. каждому 𝑉⃗⃗ = 0⃗⃗ удлинению, согласно закону Гука, соответствует определенная упругая сила: 𝐹⃗тяж 𝐹упр = 𝑘|𝑥|). 2) Динамический – измеряют ускорение, которое сообщает телу измеряемая сила, и рассчитывают, согласно определению силы 𝐹⃗ = 𝑚𝑎⃗. II закон Ньютона. 1. Если на тело действует одна сила. 𝐹⃗ = 𝑚𝑎⃗ - II закон Ньютона 𝑎⃗ m 𝐹⃗ В инерциальных системах отсчета вектор силы, действующей на тело равен произведению массы этого тела на вектор ускорения, сообщаемый этой силой телу. 2. Если на тело действует несколько сил. Если тело под действием нескольких сил двигается с ускорением, то, очевидно, в создание этого ускорения вносит вклад каждая сила, действующая на тело (каждое тело, взаимодействующее с данным телом). На основе опытов был установлен принцип независимости действия сил (принцип суперпозиции): каждая сила, действующая на тело, сообщает ему свое ускорение, независимо от действия других сил. 𝐹⃗1 сообщает 𝑎⃗1 ; 𝐹⃗2 сообщает 𝑎⃗2 . Ускорение, с которым движется тело под действием нескольких сил, равно геометрической сумме ускорений, которые сообщаются телу каждой действующей на него силой: 𝑎⃗ = 𝑎⃗1 + 𝑎⃗2 | ∙ 𝑚. 𝑚𝑎⃗ = 𝑚𝑎⃗1 + 𝑚𝑎⃗2 ⇒ 𝐹⃗ = 𝐹⃗1 + 𝐹⃗2 Ускорение, которое сообщают телу несколько сил, равно ускорению, которое тело получало бы, если бы на него действовала одна сила, равная векторной сумме всех сил, действующих на тело. 𝑛 𝐹⃗ = ∑ 𝐹⃗𝑖 = 𝑅⃗⃗ 𝑎⃗ 𝑎⃗2 𝑖=1 Равнодействующая сила 𝐹⃗1 𝑎⃗1 𝑚 𝐹⃗ 𝐹⃗2 – сила, равная геометрической сумме всех сил, действующих на тело. 𝐹⃗1 + 𝐹⃗2 + ⋯ + 𝐹⃗𝑛 = 𝑚𝑎⃗1 + 𝑚𝑎⃗2 + ⋯ + 𝑚𝑎⃗𝑛 = 𝑚 ⏟ (𝑎⃗1 + 𝑎⃗2 + ⋯ + 𝑎⃗𝑛 ) ⏟ ⃗ ∑𝑛 𝑖=1 𝐹𝑖 𝑎⃗⃗ результирующее ∑𝑛𝑖=1 𝐹⃗𝑖 = 𝑚𝑎⃗ –II закон Ньютона. Геометрическая (векторная) сумма всех сил, действующих на тело, равна произведению массы на вектор ускорения, которое ⃗ ⃗ ⃗ ⃗ ⃗ сообщает ему геометрическая сумма этих сил 𝐹1 + 𝐹2 + 𝐹тяж = 0 𝐹⃗1 данному телу в инерциальной системе отсчета. 𝐹⃗2 ⃗ 𝐹тяж Если ∑𝑛𝑖=1 𝐹⃗𝑖 = ⃗0⃗ (действие всех тел на тело ⃗⃗ 𝑎⃗ = 0 ⃗⃗ ⇒ 𝑣⃗ = 𝑐𝑜𝑛𝑠𝑡 ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗. скомпенсировано), то 𝑎⃗ = 0 Полученный II закон Ньютона можно заменить тремя скалярными уравнениями: 𝑚𝑎𝑥 = 𝐹1𝑥 + 𝐹2𝑥 + ⋯ + 𝐹𝑛𝑥 𝑚𝑎𝑥 = ∑𝑛𝑖=1 𝐹𝑖𝑥 𝑚𝑎𝑦 = 𝐹1𝑦 + 𝐹2𝑦 + ⋯ + 𝐹𝑛𝑦 𝑚𝑎𝑦 = ∑𝑛𝑖=1 𝐹𝑖𝑦 𝑚𝑎𝑧 = 𝐹1𝑧 + 𝐹2𝑧 + ⋯ + 𝐹𝑛𝑧 𝑚𝑎𝑧 = ∑𝑛𝑖=1 𝐹𝑖𝑧 ____________________ *Запишем II закон Ньютона: 𝐹⃗ = 𝑚𝑎⃗ 𝑎⃗ = ⃗⃗−𝑣 ⃗⃗⃗⃗⃗ 𝑣 0 ∆𝑡 ⃗⃗−𝑣 ⃗⃗⃗⃗⃗ 𝑣 ⇒ 𝐹⃗ = 𝑚 ∆𝑡 0 ⇒ 𝐹⃗ ∆𝑡 = 𝑚𝑣⃗ − 𝑚𝑣 ⃗⃗⃗⃗⃗0 ⇒ 𝐹⃗ ∆𝑡 = 𝑝⃗ − ⃗⃗⃗⃗⃗ 𝑝0 𝐹⃗ ∆𝑡 = ∆𝑝⃗ – II закон Ньютона в импульсной форме. где ∆𝑡 - время действия силы (время взаимодействия тел); 𝐹⃗ ∆𝑡 – вектор импульса силы; ∆𝑝⃗ - вектор изменения импульса тела. II закон Ньютона в импульсной форме: вектор импульса силы равен изменению вектора импульса тела (материальной точки). II закон Ньютона в импульсной форме справедлив для сил, не меняющихся во времени (мгновенные силы, удар). Его можно обобщить на случай, когда сила меняется во времени. Для этого промежуток времени действия силы нужно разбить на столь малые интервалы ∆𝑡𝑖 , чтобы на каждом из них значение силы без большой ошибки можно было считать постоянным. Для каждого малого интервала справедлив полученный закон. Суммируя изменение импульсов за малые интервалы времени, получим: ∑𝑛𝑖=1 𝐹⃗𝑖 ∆𝑡𝑖 = ∆𝑝⃗ Геометрическая сумма импульсов сил равна изменению вектора импульса тела (материальной точки).