Игры и выигрышные стратегии в профильном курсе информатики

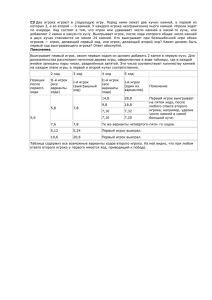
ИГРЫ И ВЫИГРЫШНЫЕ СТРАТЕГИИ В КУРСЕ ПРОФИЛЬНОЙ
ШКОЛЫ.
Шанина Т.А.
учитель информатики и ИКТ
МОУ Борисоглебская СОШ №4
[email protected]
В настоящее время в курсе профильной школы большое внимание уделяется
вопросам, входящим в задания единого государственного экзамена. Не стал
исключением и предмет Информатика и ИКТ. В Стандарте для профильных
классов средней школы упоминается такая тема, как игры и выигрышные стратегии.
Начиная с 2005 года задачи данной тематики являются основой части С ЕГЭ,
изначально это были задания С4, а с 2007 года - С3. Как же подготовить ученика к
восприятию данной темы и наиболее результативной работе по решению типовых
задач.
Прежде всего, необходимо сформировать у детей понятие игры. Определимся
сразу, что мы будем рассматривать не все игры, а только их определенный класс.
Нас будут интересовать игры с противоречивыми интересами сторон
(антагонистические игры) и полной информацией об игре, и в первую очередь такая
разновидность подобных игр, как игра двух лиц с нулевой суммой.
Игра двух лиц (в дальнейшем будем называть их первый игрок и второй
игрок, подразумевая игроков, которые ходят первым и вторым соответственно) с
нулевой суммой означает, что выигрыш одного игрока является проигрышем
другого (в ряде игр возможна ничья). В рассматриваемых нами играх участвуют два
игрока, которые ходят по очереди, причем оба они обладают полной информацией о
текущей игровой ситуации (это определение исключает большинство карточных
игр) и о возможных ходах очередного игрока. Игра считается оконченной, если
достигнута позиция, являющаяся согласно правилам игры “терминальной”
(конечной, заключительной), например, матовая позиция в шахматах. Примерами
рассматриваемых нами игр являются большинство настольных игр: шахматы,
шашки, го, крестики-нолики, реверси и многие другие. В математике большое
распространение получили игры с камнями, в которых в распоряжении двух игроков
имеются несколько кучек камней (одна или более). Игроки ходят по очереди. Также
определено, сколько камней и из какого количества кучек может взять игрок за один
ход. Если за один ход можно взять любое ненулевое число камней, но только из
одной из кучек, то такая игра называется ним.
После того как было сформировано понятие игры, необходимо уделить
внимания вопросам, связанным со стратегией игры.
Пусть в нашей игре не бывает “ничьих” и игроки ходят по очереди. Позиция
называется выигрышной, если в ней существует какой-нибудь разрешенный ход,
приводящий к выигрышу. С другой стороны, некоторая позиция является
проигранной для игрока, если все разрешенные ходы из этой позиции ведут к
позициям, в которых возможен выигрыш противника. Стратегией в конечной игре с
полной информацией называется правило, указывающее, как следует игроку ходить
в каждой из позиций, где ход за ним. Понятие стратегии не надо отождествлять с
понятием хода. Стратегия определяет полный план действий игрока при
всевозможных ситуациях, могущих возникнуть в игре.
Стратегия называется выигрышной для игрока, если все партии, в которых он
придерживается этой стратегии, заканчиваются выигрышем этого игрока. Конечную
игру с полной информацией можно представить в виде ориентированного графа,
вершинами которого являются все допустимые позиции игры, а ребра указывают
возможные ходы. Данный граф обязательно будет ациклическим (не будет
содержать циклов), в противном случае окончание игры не гарантировано.
Для ряда игр просчитывать большое число позиций для определения
результата игры не требуется. В них удается выигрышную стратегию описать с
помощью простой функции, аргументом которой является позиция, а значением —
выигрышный ход для данной позиции или сообщение о том, что позиция является
проигрышной. Рассмотрим пример такой игры.
На столе лежат N камней. Играющие по очереди могут взять от одного до
четырех камней. Кто не может сделать ход (камней не осталось) — проигрывает.
Если N делится на 5 без остатка, то второй игрок может гарантировать себе
выигрыш, дополняя ход противника до 5 (если первый взял одну, то второй берет
четыре и т.д.). Если N на 5 не делится, то выигрывает первый игрок: он должен
сначала взять число камней, равное остатку от деления N на 5, а потом дополнять
ход противника до 5. Здесь все позиции с числом камней кратным 5 являются
проигрышными, остальные — выигрышными. Программирование выигрышной
стратегии для такой игры не составит труда.
В настоящее время в заданиях ЕГЭ по информатике выделяют несколько
типов задач по определению выигрышной стратегии.
a) Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в
первой из которых 3, а во второй – 2 камня. У каждого игрока неограниченно
много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или
увеличивает в 3 раза число камней в какой-то куче, или добавляет 1 камень в
какую-то кучу. Выигрывает игрок, после хода которого общее число камней в
двух кучах становится не менее 16 камней. Кто выигрывает при безошибочной
игре – игрок, делающий первый ход, или игрок, делающий второй ход? Каким
должен быть первый ход выигрывающего игрока? Ответ обоснуйте (демо-версия
ЕГЭ, 2007 год)
b) Два игрока играют в следующую игру. На координатной плоскости стоит фишка.
В начале игры фишка находится в точке с координатами (–2,–1). Игроки ходят
по очереди. Ход состоит в том, что игрок перемещает фишку из точки с
координатами (x,y) в одну из трех точек: (x+3,y), (x,y+4), (x+2,y+2). Игра
заканчивается, как только расстояние от фишки до начала координат превысит
число 9. Выигрывает игрок, который сделал последний ход. Кто выигрывает при
безошибочной игре – игрок, делающий первый ход, или игрок, делающий второй
ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте
(демо –версия ЕГЭ, 2010 г)
Решение этих типов задач основано на построении дерева игры, которое
удобно записывать в виде таблицы. Решение задачи 2 может быть представлено
следующим образом:
Выигрывает первый игрок, своим первым ходом он должен поставить фишку
в точке с координатами (1,-1). Для доказательства рассмотрим неполное дерево
игры, оформленное в виде таблицы, где в каждой ячейке координаты фишки на
каждом этапе игры.
1 ход
2 ход
3 ход
Позиция
II-й
игрок I-й
после
(все
игрок(выигрышный
первого хода варианты
ход)
хода)
1,–1
3,1
5,3
1,3
5,3
4,-1
4,3
Таблица 1. Решение задачи 2.
4 ход
5 ход
II-й
игрок I-й
игрок
(все
(один
из
варианты
вариантов)
хода)
8,3
11,3
5,7
8,7
7,5
10,5
7,3
10,3
4,7
7,7
6,5
9,5
Те же варианты 3,4 ходов
Таблица содержит все возможные варианты ходов второго игрока. Из неё
видно, что при любом ответе второго игрока у первого имеется ход, приводящий к
победе.
Задание С3 проверяет умение построить дерево игры по заданному алгоритму и
обосновывать выигрышную стратегию. Это задание высокой сложности,
оцениваемое в 3 первичных балла.
Диаграмма1. Процент выполнения задания С3.
Типичные ошибки учащихся, допущенные при выполнении задания С3:
- неверно вычисляется или вообще не вычисляется расстояние от фишки до начала
координат;
- неверно указан выигрывающий игрок;
- отсутствует описание выигрышной стратегии;
- отсутствует доказательство или рассмотрение вариантов принципиальных ходов,
т.е. потеряны варианты возможных шагов игравших, принципиально меняющие
характер развития событий.
Решение может быть оформлено по-разному: в виде таблиц, графов, словесного
описания, и т.д. Стратегия правильного решения в работе экзаменуемого может
быть представлена в варианте отличном от «образцового», но основные положения
должны совпадать с предложенным.
Ранее подобные задачи встречались лишь на олимпиадах по информатике и
программированию и опирались на знания, полученные учащимися математических
классов в углубленном курсе математики. Изучение темы “Игры и выигрышные
стратегии” позволяет показать ученику научный подход к решению ряда бытовых
задач, расширяет их кругозор с точки зрения практической применимости знаний
математики и алгоритмов.
Список использованной литературы:
1.
Демонстрационный вариант контрольных измерительных материалов единого государственного
экзамена 2010 года по информатике и ИКТ
2.
Демонстрационный вариант контрольных измерительных материалов единого государственного
экзамена 2007 года по информатике и ИКТ
3.
А. Шеня. Игры и стратегии с точки зрения математики. М. Изд-во МЦНМО, 2007 год
4.
http://inf.1september.ru/ Энциклопедия учителя информатики