Задание 3
Рассчитать и построить зависимости средней длины свободного пробега, времени
релаксации и электропроводности от температуры для металла в диапазоне
температур (0,1- 10) ТD (Приложение MCAD №3). Оценить степень дефектности
металла по заданной величине удельного сопротивления.
3.1 Исследование температурной зависимости длины свободного пробега
( )=
= 3,16 ⋅ 10
( )=
0.1
50
, при
пл
, при
пл
м,
≫
= 400 ,
581 914 ⋅ 10
2,90957 ⋅ 10
пл
, при
400
≪
= 3683 К
≫
, при
≪
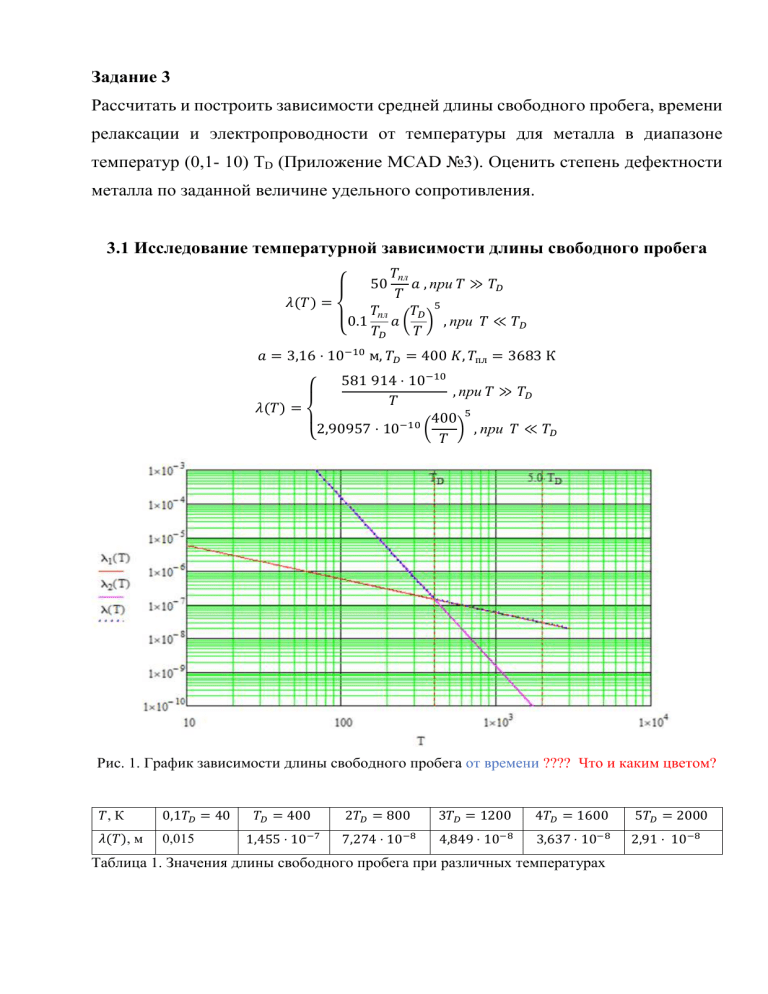
Рис. 1. График зависимости длины свободного пробега от времени ???? Что и каким цветом?
,К
( ), м
0,1
0,015
= 40
= 400
1,455 ⋅ 10
&
2
= 800
7,274 ⋅ 10
'
3
= 1200
4,849 ⋅ 10
'
4
= 1600
3,637 ⋅ 10
'
Таблица 1. Значения длины свободного пробега при различных температурах
5
= 2000
2,91 ⋅ 10
'
3.2 Исследования влияния дефектов на время релаксации
Концентрация носителей заряда ( = 0,3802 ⋅ 10) электрон/м)
Время релаксации для рассеяния на дефектах выберем из следующих расчетов.
Удельное сопротивление вольфрама при температуре 300 К по заданию:
2 = 5,3 мкОм ⋅ см = 5,3 ⋅ 10
'
Ом ⋅ м
Тогда электропроводность вольфрама при температуре 300 К будет составлять
5(300 ) =
Из формулы 5( ) =
@A (300 ) =
1
1
=
= 0,1887 ⋅ 10' См/м
'
2 5,3 ⋅ 10 Ом ⋅ м
7 8 9: ;< (=)
>?
выразим время релаксации:
5(300 )B7 0,1887 ⋅ 9,1072
=
⋅ 10('
D
D
1,6 ⋅ 0,3802
C (
) E)F ) )
= G, HIJKJ ⋅ GL
GK
M
Скорость электронов на поверхности Ферми для Вольфрама:
S
ℎ Q3R D (
1,3806 ⋅ 10 D) ⋅ Q3 ⋅ (3,14)D ⋅ 0,3802 ⋅ 10)
NO =
=
= 2,594 ⋅ 10T м/с
)
2RB7
2 ⋅ 3,14 ⋅ 9,1072 ⋅ 10
S
Длина свободного пробега при температуре 300 К:
(300 ) = @A (300) ⋅ NU = 1,76545 ⋅ 10
V
⋅ 2,594 ⋅ 10T = 4,5795 ⋅ 10
'
м
Что составляет k=457,95/3,16=145 шагов кристаллической решетки Вольфрама.
Зададим число шагов решетки, на котором встречается дефект:
@деф =
деф
деф /NO
100
1,21 ⋅ 10
V
1000
1,21 ⋅ 10
)
10 000
1,21 ⋅ 10
D
Тогда зависимость времени релаксации для электрон-фононного рассеяния будет
иметь вид
@U ( ) =
( )
NU
Суммарное время релаксации по правилу Маттиссена:
@A ( ) = Y@Z ( )
+ @U ( ) \
Рис. 2. График зависимости времени релаксации от температуры при @деф = 1,2 ⋅ 10
V
M
Рис. 8. График зависимости времени релаксации от температуры при @деф = 1,2 ⋅ 10
)
M
По графикам видно, что к значению @A (300 ) = 1,76545 ⋅ 10
V
M
наиболее приближен первый график. Следовательно, дефекты встречаются
приблизительно через каждые 100 шагов решетки.
График, соответствующий значению @A (300 ) = 1,76545 ⋅ 10
получается при τдеф = 1,92 ⋅ 10
V
c.
V
Рис. 9. График зависимости времени релаксации от температуры при @деф = 1,92 ⋅ 10
деф
= τдеф ⋅ NO = 1,92 ⋅ 10
V
⋅ 2,594 ⋅ 10T = 4,98 ⋅ 10
'
= 157
M
V
M
Соответственно, дефект в вольфраме встречается примерно через каждые
157 шагов решетки. А электрон-фононное? Сопротивление вольфрама в большей
??? степени обусловлено электрон-фононным взаимодействием.
Предельное значение времени релаксации для абсолютно чистого (без
дефектного) материала Вольфрама при температуре 300К составляет @U = 5,6 ⋅
10
V
M. ? ? ? А по моему это красная точка на Рис.9 и совсем другое значение…
Уточняйте работу.
3.3 Исследование температурной зависимости электропроводности и
теплопроводности металлов
Зависимость электропроводности металла от температуры определяется по
формуле
C D ( @A ( )
5( ) =
B7
Теплопроводность связана с электропроводностью по закону Видемана-Франца:
`( ) = a
1 Rc
5( ) , где a =
3 C
D
Рис. 10. График зависимости электропроводности и теплопроводности от температуры при @деф =
1,92 ⋅ 10
V
M
@деф = 1,92 ⋅ 10
)
M
Рис. 11. График зависимости электропроводности и теплопроводности от температуры при
Рис. 12. График зависимости электропроводности и теплопроводности от температуры при @деф =
1,92 ⋅ 10
D
M
Что можно сказать о зависимости теплопроводности и электропроводности
от температуры при высокой и при низкой дефектности материала.
Сравните с реальными значениями электропроводности и
теплопроводности при 300К.
3.4. Исследование электропроводности на высоких частотах
Электропроводность твердых тел как функция частоты ω переменного
электрического поля определяется выражением:
5(d) =
5(0)
1 + dD@ D
Рис. 3. График зависимости электропроводности от частоты
Что
можно
сказать
рассматривая
график
Рис.13?
До
каких
частот
электропроводность не изменяется? Когда влияние частоты становится
значительным? А связаны между собой длинна свободного пробега электрона и
частота? И как это связано с дефектностью материала?