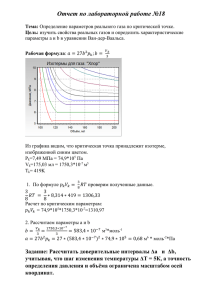
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ. СОСТАВЛЕНИЕ ОПТИМАЛЬНОГО ПЛАНА.
Математическая модель:
Пусть
Х1 – (га) площадь, которую необходимо засеять картофелем,
Х2 – (га) площадь, которую необходимо засеять свеклой.
Целевая функция – прибыль от реализации картофеля и свеклы, собранных с площади х1 и площади х2,
соответственно:
𝐹(𝑥) = 1250𝑥1 + 1750𝑥2 → 𝑚𝑎𝑥
При условии 𝑥1 ≥ 0, 𝑥2 ≥ 0
И ограничениях:
По трудовым ресурсам
По расходу удобрений
20𝑥1 + 10𝑥2 ≤ 10000
2𝑥1 + 3𝑥2 ≤ 1800
По расходу минеральных веществ
𝑥1 + 2𝑥2 ≤ 1000
По площади для засевания
𝑥1 + 𝑥2 ≤ 850
Таким образом, математическая модель этой задачи имеет вид
𝐹(𝑥) = 1250𝑥1 + 1750𝑥2 → 𝑚𝑎𝑥
20𝑥1 + 10𝑥2 ≤ 10000
2𝑥1 + 3𝑥2 ≤ 1800
𝑥1 + 2𝑥2 ≤ 1000
𝑥1 + 𝑥2 ≤ 850
{ 𝑥1 ≥ 0, 𝑥2 ≥ 0
Решение задачи симплекс-методом:
Приведем систему ограничений к каноническому виду путем введения дополнительных
переменных х3,х4, х5, х6. Получим расширенную систему:
20𝑥1 + 10𝑥2 + 𝑥3 = 10000
2𝑥1 + 3𝑥2 + 𝑥4 = 1800
{
𝑥1 + 2𝑥2 + 𝑥5 = 1000
𝑥1 + 𝑥2 + 𝑥6 = 850
Целевую функцию представим в виде
𝑍 − 1250𝑥1 − 1750𝑥2 = 0
Базисными переменными будут являться дополнительные переменныех3, х4, х5, х6.
Составим первую симплекс-таблицу:
Базис
х3
х4
х5
х6
Z
Переменные
Свободный
член
10000
1800
1000
850
0
Оценочные
отношения
х1
х2
х3
х4
х5
20
2
1
1
10
3
2
1
1
0
0
0
0
1
0
0
0
0
1
0
х6
0
0
0
1
-1250
-1750
0
0
0
0
10000 / 10
1800 / 3
1000 / 2
850 / 1
=
=
=
=
1000
600
500
850
Проверяем критерий оптимальности задачи. В последней оценочной строке имеются
отрицательные коэффициенты. Выбираем из них наибольший по модулю – (-1750).
Находим оценочные отношения и выбираем из них минимальное (=500).
Третья строка является ведущей, разрешающий элемент равен 2.
Вместо переменной 𝑥5 в базис войдет переменная 𝑥2 .
Переходим к новой симплекс-таблице:
Базис
х3
х4
х2
х6
Z
Переменные
Свободный
член
5000
300
500
350
875000
Оценочные
отношения
х1
х2
х3
х4
х5
15
1/2
1/2
1/2
0
0
1
0
1
0
0
0
0
1
0
0
-5
-3/2
1/2
-1/2
х6
0
0
0
1
-375
0
0
0
875
0
5000 / 15
300 / 1/2
500 / 1/2
350 / 1/2
= 333 1/3
=
600
=
1000
=
700
Проверяем критерий оптимальности задачи. В последней оценочной строке имеются
отрицательные коэффициенты. Выбираем из них наибольший по модулю – (-375).
1
Находим оценочные отношения и выбираем из них минимальное (=333 3).
Первая строка является ведущей, разрешающий элемент равен 15.
Вместо переменной 𝑥3 в базис войдет переменная 𝑥1 .
Переходим к новой симплекс-таблице:
Базис
Переменные
Свободный
член
х1
х4
х2
х6
Z
1000/3
400/3
1000/3
550/3
1000000
х1
х2
х3
х4
х5
1
0
0
0
0
0
1
0
1/15
-1/30
-1/30
-1/30
0
1
0
0
-1/3
-4/3
2/3
-1/3
х6
0
0
0
1
0
0
25
0
750
0
В последней строке нет отрицательных значений, значит оптимальное решение найдено.
х1 =
1000
3
х2 =
1000
3
Максимальное значение целевой функции:
𝐹(𝑥) = 1250 ∗
1000
1000
+ 1750 ∗
= 1000000
3
3
1
Вывод: для получения оптимальной прибыли F=1000000 руб необходимо засеять 333 3 га картофелем и
1
1
1
333 3 га свеклой. При этом 183 3 га площади останется незасеянной и 133 3 т удобрений не будет
израсходовано.
Обозначим филиалы в Михайловке, Урюпинске и Котельниково предприятиями № 1, 2 и 3,
соответственно.
Обозначим xk количество средств, выделенных k-тому предприятию.
Начинаем рассматривать распределение средств с 3-го предприятия.
Для нахождения решения составляем таблицу, где обозначим:
k – номер предприятия, k = 1,2,3;
xk – средства, отданные k –тому предприятию;
sk – средства, оставшиеся после k -того шага, т.е. после распределения средств между
предприятиями 3,..., k;
fk (хk) – прибыль, полученная от вложения в k –тое предприятие средств хk ;
Zk *(sk-1) – условная оптимальная прибыль, полученная на k -том шага после
распределения средств, оставшихся после предыдущих шагов.
хk*(sk-1) – распределённые на k -том шаге средства, при которых прибыль Zk*(sk-1)
получается максимальной.
sk-1
0
1
2
3
4
5
k=2
xk –
средства,
выдел-ые
k предпр.
sk
0
0
1
0
1
0
1
0
2
1
2
0
1
2
0
3
2
1
3
0
1
2
3
0
4
3
2
1
4
0
1
2
3
4
0
5
4
3
2
1
5
0
f 2 (х2) + Z3*(s2)
0
0+0,10=0,10
0,20+0 = 0,20
0 +0,40 = 0, 40
0,20 + 0,10 = 0,30
0,40 + 0 = 0,40
0 + 0,70 = 0,70
0,20 + 0,40 = 0,60
0,40 + 0,10 = 0,50
0,60 + 0 = 0,60
0 + 0,75 = 0,75
0,20 + 0,70 = 0,90
0,40 + 0,40 = 0,80
0,60 + 0,10 = 0,70
0,80 + 0 = 0,80
0 + 0,90 = 0,90
0,20 + 0,75 = 0,95
0,40 + 0,70 = 1,10
0,60 + 0,40 = 1,00
0,80 + 0,10 =0,90
1,00 + 0 = 1, 00
k=1
Z2*(s1) х2*(s1)
0
0
0,20
0,40
1
0,70
0
0,90
1
1,10
2
f 1 (х1) + Z2*(s1)
0
0 + 0,20 = 0,20
0,15 + 0 = 0,15
0 + 0,40 = 0,40
0,15 + 0,20 = 0,35
0,30 + 0 = 0,30
0 + 0,70 = 0,70
0,15 + 0,40 = 0,55
0,30 + 0,20 = 0,50
0,45 + 0 = 0,45
0 + 0,90 = 0,90
0,15 + 0,70 = 0,85
0,30 + 0,70 = 1,00
0,45 + 0,20 = 0,65
0,60 + 0 = 0,60
0 + 1,10 = 1,10
0,15 + 0,90 = 1,05
0,30 + 0,70 = 1,00
0,45 + 0,40 = 0,85
0,60 + 0,20 = 0,80
0,75 + 0 =0,75
Z1*(s0) х1*(s0)
0
0,20
0
0
0,40
0
0,70
0
1, 00
2
1,10
0
Таким образом, максимальная прибыль составит 1,10 млн. руб. Эта прибыль достигается при следующем
распределении инвестиций:
3 млн. рублей выделить филиалу в Котельниково (третий филиал);
2 млн рублей выделить филиалу в Урюпинске (второй филиал);
Филиалу в Михайловке (второй филиал) не выделять денежных средств.
Прибыль складывается следующим образом: 0 + 0,40 + 0,70 = 1,10 руб.