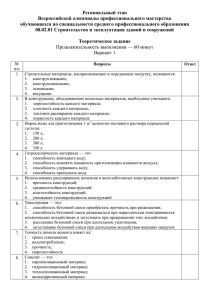
Министерство образования и науки Российской Федерации Тольяттинский государственный университет Архитектурно-строительный институт Кафедра «Городское строительство и хозяйство» В.А. Филиппов ПРОЕКТИРОВАНИЕ КОНСТРУКЦИЙ ЖЕЛЕЗОБЕТОННЫХ МНОГОЭТАЖНЫХ ПРОМЫШЛЕННЫХ ЗДАНИЙ Электронное учебно-методическое пособие рмирование опорных зон второстепенных балок представлено с. 5.6. Раскладка сеток армирования плиты и опорных сеток степенной балки показана на рис. 5.7. – 109 – 600 первого пролета Рис. 4.3. Эпюра материалов ригеля 200 ISBN 978-5-8259-0825-0 Рис. 4.4. Схема расположения нижней Рис. 6.8. Армирование консолей крайних колонн: 1 – концевой; 2 – промежуточной; 4 – хомуты; 1 арматуры 200 200 6, 7 – наклонная арматура консоли; 11 – закладная деталь консоли; 13 – арматура консоли; 17 – металлические пластины b <(=)3000 b >3000 1-1 l – 71 – l 600 l 200 нструкция пустотной панели: 1 – каркасы с поперечной брах панели; 2 – сетки косвенного армирования, усиления силия предварительного напряжения; 4 – конструктивная ования верхней полки; 5 – продольная предварительно 2 женная рабочая арматура; 6 – строповочная петля ФГБОУ ВПО «Тольяттинский государственный университет», 2015 1 1 УДК 624.012.45(075.8) ББК 38.53 Рецензенты: начальник бюро сопровождения проектов Проектного управления ОАО «АВТОВАЗ» А.В. Казаринов; канд. техн. наук, доцент Тольяттинского государственного университета В.И. Булгаков. Филиппов, В.А. Проектирование конструкций железобетонных многоэтажных промышленных зданий : электронное учеб.-метод. пособие / В.А. Филиппов. – Тольятти : Изд-во ТГУ, 2015. – 140 с. – 1 оптический диск. Приведены методика, последовательность и примеры расчета и конструирования железобетонных конструкций многоэтажных промышленных зданий, включая расчет фундаментов. Учебно-методическое пособие написано в соответствии с программой курса «Железобетонные и каменные конструкции» и предназначено для курсового и дипломного проектирования направления подготовки бакалавров 270800.62 «Строительство». Текстовое электронное издание. Рекомендовано к изданию научно-методическим советом Тольяттинского государственного университета. рмирование опорных зон второстепенных балок представлено с. 5.6. РаскладкаМинимальные сеток армирования плитытребования: и опорных IBM сетокPC-совместимый системные степенной балки показана на рис. 5.7. компьютер: Windows XP/Vista/7/8; PIII 500 МГц или эквивалент; 128 Мб ОЗУ; SVGA; Adobe Reader. 600 первого пролета Рис. 4.3. Эпюра материалов ригеля l 200 нструкция пустотной панели: 1 – каркасы с поперечной брах панели; 2 – сетки косвенного армирования, усиления силия предварительного напряжения; 4 – конструктивная ования верхней полки; 5 – продольная предварительно 2 ФГБОУ ВПО «Тольяттинский женная рабочая арматура; 6 – строповочная петля 1 1 Рис. 4.4. Схема расположения нижней 1 арматуры 200 200 b <(=)3000 1-1 l b >3000 – 71 – l 600 200 государственный университет», 2015 Редактор Г.В. Данилова Технический редактор З.М. Малявина Компьютерная верстка: Л.В. Сызганцева Художественное оформление, компьютерное проектирование: И.И. Шишкина Дата подписания к использованию 29.01.2015. Объем издания 10,45 Мб. Комплектация издания: компакт-диск, первичная упаковка. Заказ № 1-03-14. рмирование опорных зон второстепенных балок представлено с. 5.6. Раскладка сеток армирования плиты и опорных сеток Издательство государственного университета степенной балки показанаТольяттинского на рис. 5.7. 445667, г. Тольятти, ул. Белорусская, 14, тел. 8 (8482) 53-91-47, www.tltsu.ru 600 первого пролета Рис. 4.3. Эпюра материалов ригеля 200 нструкция пустотной панели: 1 – каркасы с поперечной брах панели; 2 – сетки косвенного армирования, усиления силия предварительного напряжения; 4 – конструктивная ования верхней полки; 5 – продольная предварительно женная рабочая арматура; 6 – строповочная петля 1 l 2 Рис. 4.4. Схема расположения нижней 1 арматуры 200 200 b <(=)3000 1-1 l b >3000 – 71 – l 600 200 1 Содержание ВВЕДЕНИЕ ..........................................................................................6 1. ОБЩИЕ СВЕДЕНИЯ О МНОГОЭТАЖНЫХ ПРОМЫШЛЕННЫХ ЗДАНИЯХ .....................................................8 1.1. Габаритные схемы зданий, привязка колонн и наружных стен к разбивочным осям .................................8 1.2. Конструктивное решение ....................................................10 1.3. Нагрузки на каркасы зданий ...............................................14 2. ПРОЕКТИРОВАНИЕ РЕБРИСТОЙ ПАНЕЛИ ПЕРЕКРЫТИЙ .......16 2.1. Расчетный пролет и нагрузки ..............................................17 2.2. Усилия от расчетных и нормативных нагрузок ...................18 2.3. Расчетное сечение панели ...................................................19 2.4. Характеристики прочности бетона и арматуры ..................20 2.5. Расчет панели по первой группе предельных состояний ...20 2.6. Расчет ребристой панели по второй группе предельных состояний ........................................................28 2.7. Конструкция типовой ребристой плиты перекрытия ........36 3. ПРОЕКТИРОВАНИЕ ПУСТОТНОЙ ПАНЕЛИ ПЕРЕКРЫТИЯ .......39 3.1. Конструкция типовой пустотной панели ...........................39 3.2. Расчетный пролет, нагрузки и усилия в плите ....................40 3.3. Характеристики прочности бетона и арматуры ..................41 3.4. Расчет пустотной панели по первой группе предельных состояний ........................................................42 3.5. Расчет пустотной панели по второй группе предельных состояний .......................................................48 3.6. Конструкция типовой пустотной панели перекрытия ......53 4. ПРОЕКТИРОВАНИЕ РИГЕЛЯ .............................................................56 4.1. Расчетная схема и нагрузки ................................................56 4.2. Вычисление изгибающих моментов в расчетных сечениях ригеля ..............................................57 4.3. Расчет прочности ригеля по сечениям, нормальным к продольной оси ................................................................64 4.4. Расчет прочности ригеля по сечениям, наклонным к продольной оси ............................................66 –4– 4.5. Конструирование арматуры крайнего ригеля ....................68 4.6. Конструкция типового ригеля ...........................................73 5. ПРОЕКТИРОВАНИЕ РЕБРИСТОГО МОНОЛИТНОГО ПЕРЕКРЫТИЯ С БАЛОЧНЫМИ ПЛИТАМИ ..............................78 5.1. Компоновка конструктивной схемы ребристого монолитного перекрытия с балочными плитами .............78 5.2. Расчет монолитной плиты перекрытия .............................78 5.3. Расчет второстепенной неразрезной балки .......................83 6. РАСЧЕТ КРАЙНЕЙ КОЛОННЫ .....................................................93 6.1. Определение усилий в колонне ..........................................93 6.2. Расчет продольной арматуры колонны...............................96 6.3. Примеры конструирования типовых колонн ...................102 7. ПРОЕКТИРОВАНИЕ ФУНДАМЕНТОВ ПОД КОЛОННЫ .............112 7.1. Общие положения ..............................................................112 7.2. Определение геометрических размеров фундамента .......113 7.3. Проверка несущей способности фундамента ...................117 7.4. Определение сечений арматуры плитной части фундамента ..............................................................119 7.5. Пример расчета фундамента .............................................123 Библиографический список ...........................................................129 Приложение ...................................................................................131 –5– ВВЕДЕНИЕ Всемерное развитие производства, повышение его эффективности – основа технической политики современного государства. Требования, предъявляемые к промышленному строительству, к его способности эффективно удовлетворять запросы общества, будут систематически возрастать. Современное проектирование промышленных предприятий представляет собой сложный процесс, учитывающий и взаимосвязывающий множество разносторонних факторов, степень влияния которых меняется и обусловливается конкретными заданными требованиями. Большая роль в процессе проектирования отводится системе нормативной документации и в первую очередь Строительным нормам и правилам (СНиП), регламентирующим проектную деятельность и обеспечивающим комплексный подход к решению задач при проектировании и строительстве промышленных предприятий, а также надежность и долговечность построенных объектов. Важнейшим направлением развития промышленного строительства остается создание и внедрение конструктивных типовых решений элементов зданий, а также способов их изготовления и монтажа, которые обеспечивали бы значительное повышение уровня индустриализации и снижение материалоемкости. Существенную роль в выполнении поставленных задач играет оптимальность решений, принимаемых на стадии проектирования. Практика строительства показывает, что большинство проектов промышленных объектов (более 80 % по стоимости строительномонтажных работ) разрабатываются с применением типовых проектных материалов. Переход проектных организаций на проектирование с широким использованием типовых материалов ставит ряд проблем, главная из которых – создание высокоэкономичных типовых конструкций, в наибольшей степени отвечающих современным требованиям. –6– Расчеты показывают, что за счет совершенствования конструктивных элементов может быть достигнуто не менее 30–40 % повышения производительности труда, а также значительное снижение материалоемкости зданий, которое в результате изменившихся в настоящее время требований к промышленным зданиям непрерывно увеличивается. С использованием унифицированных параметров строится подавляющее большинство промышленных объектов. Доля многоэтажных промышленных зданий в общем объеме промышленного строительства составляет около 40 %, из которых большая часть приходится на здания с железобетонным каркасом. В номенклатуру железобетонных изделий включены конструкции, набор которых полностью обеспечивает проектирование и строительство многоэтажных промышленных зданий с объемно-планировочными решениями, соответствующими унифицированным габаритным схемам. Целью данного учебно-методического пособия является изложение методики расчета и конструирования (с примерами расчета) типовых конструкций многоэтажных промышленных зданий в соответствии с требованиями свода правил СП 63.13330.2012 «Бетонные и железобетонные конструкции. Основные положения». При выполнении курсового или дипломного проекта помимо представленного методического пособия необходимо пользоваться соответствующими строительными нормами (СНиП), сводами правил (СП) к ним и пособиями к сводам правил. Курсовое и дипломное проектирование многоэтажных промышленных зданий является важным этапом подготовки инженера-строителя. В процессе работы над проектом студент углубленно изучает и разрабатывает унифицированные схемы зданий, рассчитывает типовые конструкции, применяет на практике теоретические знания в решении конкретных задач, приучается пользоваться нормативной, учебной и технической литературой. Помимо этого, при выполнении чертежей в соответствии с требованиями ЕСКД студент закрепляет навыки конструирования железобетонных конструкций и составления спецификаций. –7– 1. ОБЩИЕ СВЕДЕНИЯ О МНОГОЭТАЖНЫХ ПРОМЫШЛЕННЫХ ЗДАНИЯХ 1.1. Габаритные схемы зданий, привязка колонн и наружных стен к разбивочным осям Для зданий с сеткой колонн 6×6 м, с перекрытиями из плит, опирающихся на полки ригелей, предусматриваются следующие габаритные схемы: а) с количеством пролетов, равным двум и более, высотой от трех до пяти этажей включительно, с высотами этажей 4,8 и 6,0 м; высотой первого этажа 6,0 м и высотой последующих этажей 4,8 м, а также высотой первого этажа 7,2 м и высотой последующих этажей 6,0 м (регулярные схемы зданий); б) с количеством пролетов, равным трем, с укрупненной сеткой колонн верхнего этажа, оборудованного подвесным транспортом или без него, высотой от трех до пяти этажей включительно, с высотами этажей 4,8 и 6,0 м и высотой верхнего этажа 7,2 м (нерегулярные схемы зданий). Для зданий с сеткой колонн 9×6 м включаются габаритные схемы: а) с количеством пролетов два и более, высотой три и четыре этажа, с высотами этажей 4,8 и 6,0 м; высотой первого этажа 6,0 м и высотой первого этажа 7,2 м и высотой последующих этажей 6,0 м (регулярные схемы зданий); б) с количеством пролетов, равным двум, с укрупненной сеткой колонн верхнего этажа, оборудованного подвесным транспортом или без него, высотой три и четыре этажа, с высотами этажей 4,8 и 6,0 м и высотой верхнего этажа 7,2 м (нерегулярные схемы зданий). Высоты этажей зданий приняты от пола одного этажа до пола следующего этажа. В верхних этажах с укрупненной сеткой колонн высота этажа принята от пола до низа стропильной конструкции. –8– Толщина пола условно принята равной 100 мм. Расстояние между продольными или поперечными температурно-усадочными швами, как правило, должно устанавливаться расчетом. Привязка колонн крайних рядов к продольным разбивочным осям здания принимается «нулевой», по колоннам средних рядов – «осевой». Привязка колонн торцевых рам зданий к поперечным разбивочным осям принята «осевой». Привязка внутренней грани торцевых стен зданий к геометрической оси колонн торцевых рам принята равной 230 мм. Привязка колонн поперечных рам у температурно-усадочных швов зданий с одинаковой сеткой колонн во всех этажах к поперечным разбивочным осям принята либо «осевой» (с применением вставок), либо со смещением геометрических осей колонн с поперечной разбивочной оси на 500 мм внутрь температурного блока (без вставок). Величина вставок назначается в конкретном проекте здания в соответствии с решением стен серии 1.030.1.-1/88*. Привязка колонн поперечных рам у температурно-усадочных швов зданий с укрупненной сеткой колонн верхнего этажа принята со смещением геометрических осей колонн с поперечной разбивочной оси на 500 мм внутрь температурного блока. Здания с одинаковой сеткой колонн во всех этажах решены с бесчердачным покрытием из ребристых плит, с плоской кровлей и внутренним водостоком. Покрытие в зданиях с укрупненной сеткой колонн верхнего этажа решено в конструкциях одноэтажных производственных зданий. Лестницы принимаются с кирпичными несущими стенами, отделенными от каркаса здания температурным швом в надземной части. Лестничные марши Z-образные серии 1.050.9-4.93. –9– 1.2. Конструктивное решение Решение пространственного каркаса зданий представляет собой сочетание рамной системы в поперечном направлении и связевой в продольном направлении. Прочность и устойчивость каркаса в поперечном направлении обеспечивается поперечными рамами, образованными сборными железобетонными колоннами и ригелями и запроектированными со всеми жесткими узлами сопряжения ригелей с колоннами, за исключением узлов сопряжений стропильной конструкции с колоннами в зданиях с укрупненной сеткой колонн верхнего этажа 18×6 м, которые приняты шарнирными. Стык ригеля с колонной предусматривает опирание ригеля на консоль колонны треугольного очертания. Жесткое сопряжение ригелей перекрытия с колоннами осуществляется при помощи ванной сварки выпусков арматуры из колонн и ригелей, сварки закладных изделий ригеля к консоли колонны и последующего замоноличивания стыка. Соединение опорной арматуры с колонной в стыках, расположенных в уровне покрытия регулярных схем зданий, выполняется с помощью стыковых стержней, которые укладываются поверх оголовка колонны и привариваются ванной сваркой с выпусками опорной арматуры ригеля, а затем электродуговой сваркой привариваются к оголовку колонны. Стыки колонн запроектированы жесткими и предусматривают соединение вертикальных выпусков арматуры из колонн с помощью ванной сварки встык. Замоноличивание стыка происходит после установки хомута в уровне ванной сварки и арматурных изделий. Стыки колонн расположены на высоте 1,8 м от отметки верха консолей. Глубина заделки колонн в стаканы фундаментов принимается равной 600 мм. Отметка верха стакана фундамента принята равной – минус 0,15 м. Прочность и устойчивость каркаса здания в продольном направлении в период монтажа и эксплуатации обеспечивается постановкой вертикальных стальных связей по колоннам. – 10 – Связи портального типа устанавливаются в продольном направлении только в одном шаге колонн, в средней части каждого температурного блока, во всех этажах здания, кроме верхнего, при регулярных схемах зданий, а в зданиях с укрупненной сеткой колонн верхнего этажа связи устанавливаются во всех этажах здания, включая верхний этаж. Связи в зависимости от высоты здания, нагрузок, требований и степени жесткости дисков перекрытий могут устанавливаться либо разряженно (через один или более рядов колонн по внутренним рядам колонн), либо по каждому ряду колонн, включая крайние ряды колонн. Междуэтажные перекрытия и покрытия выполняются из ребристых плит высотой 400 мм, опирающихся на полки ригелей или сверху на ригели прямоугольного сечения. Междуэтажные перекрытия запроектированы из плит трех типоразмеров по ширине: основные плиты – шириной 3,0 м; доборные – шириной 1,5 и 0,75 м. Доборные плиты шириной 0,75 м устанавливаются только по наружным рядам колонн. Межколонные плиты шириной 3,0 м, располагаемые по средним рядам колонн, привариваются к закладным изделиям ригелей в четырех точках. Доборные плиты шириной 0,75 м привариваются к монтажным столикам колонн и закладным изделиям ригелей. Плиты шириной 3,0 м, располагаемые в крайнем пролете рядом с доборной плитой шириной 1,5 м, привариваются в двух точках. Остальные плиты монтируются без приварки. Швы между плитами, а также между торцами плит, ригелями и колоннами должны быть тщательно заполнены бетоном класса не ниже В15. Покрытия в зданиях, сохраняющих в верхнем этаже сетку колонн нижележащих этажей, решены аналогично перекрытиям. Конструкции покрытия и монтажные узлы сопряжения конструкций в зданиях с укрупненной сеткой колонн верхнего этажа (18×6 м) принимаются как для одноэтажных производственных зданий. – 11 – Стены зданий приняты навесными или самонесущими из однослойных панелей для каркасных общественных зданий, производственных и вспомогательных зданий промышленных предприятий. При навесных панелях остекление ленточное со стальными или деревянными переплетами. Стеновые панели крепятся непосредственно к железобетонным колоннам. В торцах зданий с сеткой колонн 9×6 м, а также в пределах верхнего этажа зданий с укрупненной сеткой колонн стеновые панели крепятся непосредственно к колоннам торцевых рам и к стойкам стального фахверка поэтажной разрезки, опирающимся на ригели поперечных рам. Основные размеры и номенклатура конструкций (колонн, ригелей), на которые разработаны рабочие чертежи, приняты исходя из условий использования металлических опалубочных форм конструкций серии 1.420-12 и серий ИИ23-1/70 и ИИ23-2/70. Номенклатура конструкций (серии 1.420-35.95) каркаса включает: − колонны прямоугольного сечения 400×400 мм и 400×600 мм для зданий с высотами этажей 4,8; 6,0 и 7,2 м; − ригели таврового сечения высотой 800 мм с полками для опирания плит перекрытия и покрытия, пролетами 6,0 и 9,0 м; − ригели таврового сечения высотой 800 мм с односторонней полкой для опирания плит, пролетами 6,0 и 9,0 м, устанавливаемые в торцах зданий. В перекрытиях серии 1.420-12 предусмотрены ригели прямоугольного сечения размером 300×800 мм для зданий с сеткой колонн 6×6 м под большие нагрузки и для зданий, в которых должно устанавливаться «провисающее» оборудование, опирающееся на балки, окаймляющие проемы перекрытий. Для зданий с высотой этажей 4,8 м, а также с высотой первого этажа 6,0 м и высотой последующих этажей 4,8 м принята двухэтажная разрезка колонн нижних этажей. Для четырех- и пятиэтажных зданий разрезка колонн третьего и четвертого этажей также двухэтажная, а колонны верхнего этажа трех- и пятиэтажных зданий имеют одноэтажную разрезку. – 12 – Для зданий с высотой этажей 6,0 м, а также с высотой первого этажа 7,2 м и высотой последующих этажей 6,0 м принята двухэтажная разрезка колонн нижних этажей. Для четырехэтажных зданий разрезка колонн третьего и четвертого этажей двухэтажная. Для пятиэтажных зданий колонны третьего этажа – одноэтажной разрезки, а четвертого и пятого этажей – двухэтажной разрезки. Колонны верхнего этажа с укрупненной сеткой имеют одноэтажную разрезку. Колонны выполняются из тяжелого бетона классов по прочности на сжатие В15…В45. Продольная арматура колонн принимается из стержневой горячекатаной периодического профиля арматуры класса А400 по ГОСТ 5781–82 постоянного по длине диаметра, хомуты – из стержневой горячекатаной гладкой арматуры класса А240 по ГОСТ 5781–82. Колонны армируются пространственными каркасами, состоящими из арматурных стержней и замкнутых сварных хомутов. В состав пространственных каркасов колонн входят закладные изделия консолей колонн, стыков колонн, торцов колонн, выпусков арматуры для соединения с ригелями, закладные изделия для крепления стен, связей и т. д. Ригели пролетами 6,0 и 9,0 м серии 1.420-35.95 (выпуски 2-1 и 2-2) приняты соответственно трех типоразмеров по длине: 4980 мм (7980 мм) – крайние по месту положения в каркасе здания при сечении колонн 400×600 мм; 5280 мм (8280 мм) – крайние при сечении колонн 400×400 мм и средние при сечении колонн 400×600 мм; 5480 мм (8480 мм) – средние при сечении колонн 400×400 мм. Высота ригелей – 800 мм, ширина в уровне полок для опирания плит – 650 мм. В ригелях, устанавливаемых в торце здания, полка для опирания плит предусмотрена только с одной стороны ригеля. Ригели пролетом 6,0 м серии 1.420-35.95 (выпуск 2-1) разработаны с ненапрягаемой пролетной арматурой. В качестве рабочей арматуры (продольной и поперечной) используется стержневая горячекатаная периодического профиля арматура класса А400 по ГОСТ 5781–82. – 13 – Ригели пролетом 9,0 м серии 1.420-35.95 (выпуск 2-2) разработаны напряженными. В качестве напрягаемой пролетной арматуры в ригелях используется стержневая горячекатаная периодического профиля арматура класса А600 по ГОСТ 5781–82. В случае отсутствия на заводе-изготовителе арматурной стали класса А600 допускается применять горячекатаную периодического профиля арматуру класса А540, изготовляемую из арматурной стали класса А400 по ГОСТ 5781–82 путем упрочнения вытяжкой с контролем удлинений и напряжений. Ненапрягаемая продольная и поперечная арматура плоских каркасов ригелей пролетом 9,0 м принята из арматуры класса А400 по ГОСТ 5781–82. Напряжение стержневой арматуры ригелей пролетом 9,0 м осуществляется механическим способом на упоры форм или коротких стендов. Ригели пролетами 6,0 и 9,0 м изготавливаются из тяжелого бетона по ГОСТ 26633–91 классов по прочности на сжатие: В15…В25 – для ригелей пролетом 6,0 м; В25, В30 – для ригелей пролетом 9,0 м. Ригели армируются пространственными каркасами, объединяющими плоские арматурные каркасы, а также другие арматурные и закладные изделия. В ригелях предусмотрены закладные изделия для опирания и крепления ребристых плит перекрытий и покрытия, для крепления стальных стоек фахверка (в ригелях пролетом 9,0 м), для крепления монолитных участков (в ригелях у температурного шва), а также опорные закладные изделия для крепления ригелей к консолям колонн. 1.3. Нагрузки на каркасы зданий Промышленные здания в соответствии с ГОСТ Р 54257–2010 относятся ко второму нормальному уровню ответственности. Конструкции каркаса зданий рассчитываются на воздействие постоянных, временных длительных и кратковременных нагрузок. Постоянными нагрузками являются собственный вес железобетонных конструкций междуэтажных перекрытий и покрытия с учетом заливки швов; собственный вес конструкций кровли и пола; собс- – 14 – твенный вес наружных ограждающих конструкций, а также собственный вес колонн. Вес перегородок условно отнесен к постоянным нагрузкам. Кратковременными нагрузками являются ветровая, снеговая, от подвесного транспорта на покрытие, а также вес людей, ремонтных материалов в зоне обслуживания и ремонта оборудования. Временные длительные нагрузки – вес стационарного оборудования, вес жидкостей и твердых тел, заполняющих оборудование, вес хранимых материалов в местах, специально предназначенных для складирования и хранения материалов, а также пониженное нормативное значение снеговой нагрузки и нагрузки от подвесного транспорта на конструкции покрытия. Все временные нагрузки принимаются в виде эквивалентных равномерно распределенных нагрузок. Принятые временные нагрузки на перекрытия используются в расчетах рам каркасов с учетом коэффициентов сочетаний, соответствующих основному сочетанию нагрузок – ψ1 = 0,95; для кратковременных нагрузок – ψ2 = 0,9. При расчете конструкций без учета ветровых нагрузок и нагрузок от подвесного транспорта коэффициенты сочетаний на остальные временные нагрузки не вводятся. – 15 – 2. ПРОЕКТИРОВАНИЕ РЕБРИСТОЙ ПАНЕЛИ ПЕРЕКРЫТИЙ В курсовом проекте рассматривается вариант опирания панели на ригель прямоугольного сечения. На рис. 2.1 представлена конструкция типовой ребристой панели перекрытия для опирания на нижнюю полку ригеля таврового сечения. На рис. 2.2 изображены поперечное сечение панели и узел А. Рис. 2.1. Конструкция ребристой панели перекрытия – 16 – Рис. 2.2. Поперечное сечение панели 2.1. Расчетный пролет и нагрузки Подсчет нагрузок на 1 м2 перекрытия приведен в табл. 1. Таблица 1 2 Нормативные и расчетные нагрузки на 1 м перекрытия № п/п Норма- КоэффициРасчетные тивные ент надёжнагрузки, нагрузки, ности по кН/м2 2 кН/м нагрузке Вид нагрузки Постоянные Собственный вес плиты с залив1. кой швов 2. Конструкция пола: 2,5 1,1 2,75 керамическая плитка на цементно-песчаном растворе δ = 20 мм 18×0,02×1 = 0,36 0,36 1,3 0,468 армированная цементно-песчаная стяжка δ = 35 мм 20×0,035×1 = 0,70 0,70 1,3 0,91 песчаная засыпка δ = 70 мм 17×0,07×1 = 1,19 1,19 1,3 1,547 Итого постоянная 4,75 – 17 – 5,675 № п/п Норма- КоэффициРасчетные тивные ент надёжнагрузки, нагрузки, ности по кН/м2 2 кН/м нагрузке 15 1,2 18 Вид нагрузки 3. Временная в том числе кратковременная 4. Полная в том числе постоянная и временная длительная нагрузки 3 1,2 3,6 19,75 23,675 16,75 20,075 Расчетная нагрузка на 1 п. м плиты при ее номинальной ширине 1,5 м с учетом коэффициента надежности по ответственности здания γп = 1: − полная расчетная q = 23,675 · 1,50 · 1 = 35,51 кН/м; − полная нормативная qn= 19,75 · 1,5 · 1 = 29,62 кН/м; − постоянная и временная длительная нормативные нагрузки ql = 16,75 · 1,50 · 1 = 25,13 кН/м. Расчетный пролет плиты при ее конструктивной длине 5,98 м и ширине ригеля 300 мм q ⋅ 20 35,51 ⋅ 5,84 2 М = = = bриг 0,3 8 8 0 = 2 − − f = 6,0 − − 0,01 = 5,84 м, 2 2 где f – зазор между осью ригеля и плитой. Плита рассчитывается как однопролетная шарнирно опертая балка, загруженная равномерно распределенной нагрузкой. 2.2. Усилия от расчетных и нормативных нагрузок Усилия от полной расчетной нагрузки: − максимальный изгибающий момент в середине пролета q ⋅ 20 35,51 ⋅ 5,84 2 = = 151,36 кНм; 0,3 8 8 f = 6,0 − − 0,01 = 5,84 м, 2 − максимальная поперечная сила на опорах М= Q= q ⋅ 0 35,51 ⋅ 5,84 = = 103,68 2 2 – 18 – Mn = кН. qn ⋅ 20 29,65 ⋅ 5,84 2 = = 126,2 8 8 Усилия от нормативной нагрузки: − полной q ⋅ 2 29,65 ⋅ 5,84 2 q ⋅ 0 35,51 ⋅ 5,84 = 126,28 кНм; = = 103,68 M n = n 0 = 8 8 2 2 − постоянной и длительной временной Ml = ql ⋅ 20 25,13 ⋅ 5,84 2 100 + 85 = = 107,05 кНм. b= ⋅ 2 = 185 8 8 2 2.3. Расчетное сечение панели Конструктивные параметры поперечного сечения ребристой плиты: − высота сечения – 400 мм; − конструктивная ширина – 1485 мм; − ширина продольных ребер понизу – 85 мм, поверху – 100 мм; − ширина верхней полки b′f = 1485 – 2 · 20 = 1445 мм; − толщина полки – 50 мм. В расчетах по предельным состояниям первой группы сечение панели приводится к тавровому с шириной ребра, равной (рис. 2.3): ql ⋅ 20 25,13 ⋅ 5,84 2 100 + 85 Ml = = = 107,05 b = ⋅ 2 = 185 мм. 8 8 2 Рис. 2.3. Расчетное сечение ребристой панели Отношение h′f /h = 50/400 = 0,125 > 0,1, в расчет вводится вся ширина полки b′f = 1445 мм. – 19 – Рабочая высота сечения h0 = h – ap = 400 – 40 = 360 мм. 2.4. Характеристики прочности бетона и арматуры Ребристая предварительно напряженная плита армирована стержневой арматурой класса А800 с механическим натяжением на борта формы. Норма­тивное сопротивление арматуры Rsn = 800 МПа, расчетное сопротивление –Rs = 695 МПа; модуль упругости Es = 200000 МПа. Поперечная арматура класса А240 с расчетным сопротивлением Rsw = 170 МПа (табл. П5, П6, П7, П8 приложения). Полка армируется сварными сетками из арматуры класса В500 с расчетным сопротивлением Rs = 415 МПа. Изделие подвергают тепловой обработке при атмосферном давлении. Величина предварительного напряжения арматуры принята равной σsp = 0,7Rsn = 0,7 · 800 = 560 МПа. Бетон тяжелый класса В25, соответствующий классу напрягаемой арматуры. Расчетные сопротивления бетона для расчета по первой группе предельных состояний: Rb = 14,5 МПа; Rbt = 1,05 МПа. Расчетные сопротивления бетона для расчета по второй группе предельных состояний: Rb,ser = 18,5 МПа; Rbt,ser = 1,55 МПа. Начальный модуль упругости бетона Еb = 30000 МПа (табл. П1, П2, П3 приложения). 2.5. Расчет панели по первой группе предельных состояний Расчет прочности панели по сечению, нормальному к продольной оси Расчетный изгибающий момент М = 142,37 кНм. Сечение тавровое с пол­кой в сжатой зоне. Предполагаем, что нейтральная ось проходит в полке, и сечение рассчитываем как прямоугольное с шириной, равной ширине полки. Вычисляем коэффициент αm: αm = M Rb ⋅ b f ′ ⋅ h02 = 151,36 ⋅ 10 6 = 0,0557. 14,5 ⋅ 1445 ⋅ 360 2 ξ = 1 − 1 − 2α m = 1 − 1 − 2 ⋅ 0,0557 = 0,0573. – 20 – αm = M = 151,36 ⋅ 10 6 = 0,0557. 14,5 ⋅ 1445 ⋅ 360 2 Rb ⋅ b f ′ ⋅ h02 Относительная высота сжатой зоны бетона: ξ = 1 − 1 − 2α m = 1 − 1 − 2 ⋅ 0,0557 = 0,0573. Высота сжатой зоны бетона: x = ξ · h0 = 0,0573 · 360 = 20,64 мм. Так как x < h’f, то нейтральная ось проходит в полке. Граничная высота сжатой зоны бетона (табл. П10 приложения): 0,8 0,8 = = 0,42. 695 + 400 − 560 Rs + 400 − σ sp 1 + 1+ 0,8 0,8 700 700 ξR = = = 0,42. 800 + 400 − 560 Rsn + 400 − σ sp 1 + Так как ξ < ξR1,+установка арматуры в сжатой зоне не требуется. 700 700 Площадь продольной рабочей арматуры равна ξR = AS = Rb ⋅ b′f ⋅ x γ s 3 ⋅ Rs где γs = 1,1, так как = σ sp Rs 14,5 ⋅ 1445 ⋅ 20,64 = 565,77 мм2, 1,1 ⋅ 695 = 560 q 3 22,3 ⋅1,253 = 0,81 > 0,6 . M = = = 0,907 48 48 695 Принимаем арматуру 2∅20 мм с Аs = 628 мм2 (табл. П15 приложения). Расчет армирования полки ребристой плиты Плита проектируется с поперечными ребрами при отношении пролетов полки (рис. 2.1, 2.2) l2 /l1 = 1250/1245 = 1,004 < 2, следовательно, полка рассчитывается как плита, защемленная по контуру. Нагрузка на 1 м2 полки плиты: (g + v) · γn = (4,3 + 18) · 1 = 22,3 кН/м, где g = gпола + gполки = (2,925 + 25 · 0,05 · 1,1) = 4,3 – постоянная нагрузка. Принимая l1 = l2 = 1,25 м и Ml /Msup = 1, уравнение моментов в защемленной плите примет вид: σ sp Rs = 560 q 3 22,3 ⋅1,253 = 0,81 > 0,6 M = ,907 кНм. = = 00,907 48 48 695 Полка в продольном направлении армируется стандартной сварной сеткой с рабочей арматурой класса В500 в двух направлениях. Опорный изгибающий момент по продольному ребру воспри- – 21 – нимается сеткой с поперечной рабочей арматурой В500. Расчетное сопротивление арматуры Rs = 415 МПа. Сечение полки прямоугольное, рабочая высота сечения h0 = h – a = 50 – 15 = 35 мм; M 0,907 ⋅10 6 = = 0,0409;; ξ R = 2 Rb ⋅ b ⋅ h0 14,5 ⋅1250 ⋅ 35 2 0,8 0,8 = = 0,5 Rsр 415 1+ 1+ 700 700 aR = ξR(1 – 0,5 ξR) = 0,504(1 – 0,5 · 0,504) = 0,377; αm = 0,8 0,8 = = 0,504,, Rs 415 1+ 1+ 700 700 αm < αR – установка арматуры в сжатой зоне не требуется. Площадь рабочей арматуры ξR = RB ⋅ b ⋅ h0 (1 − 1 − 2α m ) = E 200000 RS α= s = = 6,6 Eb 30000 14,5 ⋅ 1250 ⋅ 35 ⋅ (1 − 1 − 2 ⋅ 0,0409 ) 2 = = 63,8 мм . 415 AS = Принимаем сетки с шагом 200 мм ∅4 мм с As = 88 мм2 (поз. 5, 6 рис. 2.6). Геометрические характеристики приведенного сечения h0 (1 − 1 − 2α m ) Коэффициент приведения = E 200000 RS α= s = = 6,67. 30000 E 35 ⋅ (1 − 1 − 2 ⋅ 0,0409 ) b 2 = 63,8 мм . Площадь бетонного сечения. Для этого сечение разбиваем на 415 два участка – ребро и свесы (рис. 2.4). A = b · h + (b′f – b)h′f = 185 · 400 + (1445 – 185) · 50 = 137000 мм2. Площадь приведенного сечения Ared = A + aAsp = 137000 + 6,67 · 628 = 141182,5 мм2. Статический момент площади приведенного сечения относительно нижней грани: Sred = S(Ai · yi) = 185 · 400 · 200 + (1445 – 185) · 50 · 375 + + 6,67 · 628 · 40 = 38592299,2 мм3, где Аi – площадь i-го участка сечения; yi – расстояние от нижней грани до центра тяжести i-го участка сечения. – 22 – Рис. 2.4. Схема для определения геометрических характеристик приведенного сечения Расстояние от нижней грани до центра тяжести приведенного сечения y= S red ,2 38592299,2 S red 38592299 мм. = y = A = =141182 273,35,5мм=. 273,35 мм. Ared 141182red,5 Момент инерции приведенного сечения 185 ⋅ 400 3 + 185 ⋅ 400 ⋅ (273,35 − 200) 2 + + 185 ⋅12 400 ⋅ (273,35 − 200) 2 + I red = [2I i + A yi )32 ] = i ( y ⋅−400 185 I red = [ I i + Ai ( y −3 yi ) ] = 50 (1445 − 185) 12 + + (1445 − 185) ⋅ 50 ⋅ (273,35 − 375) 2 + 50 3 (1445 − 185) 12 + + (1445 − 185) ⋅ 50 ⋅ (273,35 − 375) 2 + + 6,67 ⋅ 628 ⋅ (273,35 − 40) 2 = 2276976941 мм 4 , 12 + 6,67 ⋅ 628 ⋅ (273,35 − 40) 2 = 2276976941 мм 4 , где Ii – собственный момент инерции i-го участка сечения. Потери предварительного напряжения в арматуре Первые потери предварительного напряжения: − потери от релаксации напряжений в арматуре при электротермическом способе натяжения Δσsp1 = 0,03σsp = 0,03 · 560 = 16,8 МПа. Для арматуры класса А540 – Δσsp1 = 0,0; − потери от температурного перепада между натянутой арматурой и упорами Δσsp2 = 0. Потери от деформации формы Δσsp3 и анкеров Δσsp4 при электротермическом натяжении арматуры равны нулю. Усилие обжатия с учетом первых потерь: P(1) = Asp · (ssp – Dssp(1)) = 628 · (560 – 16,8) = 310232 H = 341,13 кН. В связи с отсутствием напрягаемой арматуры в сжатой зоне бетона (A′sp = 0) эксцентриситет усилия предварительного обжатия будет равен – 23 – e0p(1) = ysp = y – ap = 273,35 – 40 = 233,35 мм. Максимальное сжимающее напряжение бетона σbp при обжатии с учетом первых потерь от силы Р(1) уsbpbp = P(1) Ared + P(1) ⋅ e0 p1 ⋅ y I red = 341130 341130 ⋅ 233,35 ⋅ 273,35 + = 11,97 МПа. 141182,5 2276976941 Рис. 2.5. Схема для определения эксцентриситета Условие σbp ≤ 0,9Rbp = 0,9 · 17,5 = 15,75 МПа выполняется, где Rbp = 0,7В = 0,7·25 = 17,5 МПа – отпускная прочность бетона. Вторые потери предварительного напряжения: − потери от усадки бетона Δσsp5 = eb,sb · Es = 0,0002 · 200000 = 40 МПа; − потери от ползучести бетона 0,8ϕb,cr ⋅ α ⋅ σ вр = еop1 ⋅ y s ⋅ Ared (1 + 0,8ϕb,cr ) 1 + α ⋅ μ sp 1 + I red 0,8 ⋅ 2,5 ⋅ 6,67 ⋅ 8,9 = 85,16 МПа, = 233,35 ⋅ 233,35 ⋅ 141182,5 1 + 6,67 ⋅ 0,0046 ⋅ 1 + (1 + 0,8 ⋅ 2,5) 2276976941 где μ – коэффициент армирования; Δσ sp 6 = Asp 628 = 0,0046; A 137000 φb,cr – коэффициент ползучести бетона (табл. П4 приложения); P(1) P(1) ⋅ eσ0 p1–⋅ yнапряжение M g y s в бетоне 341130на sp α = Es /Eb – коэффициент bp σ bp =приведения; + − = + Aredс учетомI red I red веса141182 уровне напрягаемой арматуры собственного плиты,5 341130 ⋅ 233,35 ⋅ 233,35 16,34 ⋅ 10 6 ⋅ 233,35 − = 8,9 МПа , 2276976941 2276976941 μ= = – 24 – μ= Asp A = P(1) 628 = 0,0046; 137000 P(1) ⋅ e0 p1 ⋅ y sp M g ys 341130 = + Ared I red I red 141182,5 341130 ⋅ 233,35 ⋅ 233,35 16,34 ⋅ 10 6 ⋅ 233,35 − = 8,9 МПа , 2276976941 2276976941 σ bp = + − здесь Mg – момент от собственного веса плиты, установленной на деревянных прокладках. Mg = qw 2 4,08 ⋅ 5,662 = = 16,34 кН ⋅ м, 8 8 где qw = 2,5 · 1,485 · 1,1 = 4,08 кН/м – погонная нагрузка от собственного веса плиты; ℓ – расстояние между деревянными опорными прокладками. Сумма вторых потерь Δσsp(2) = Δσsp5 + Δσsp6= 40 + 85,16 = 125,16 МПа. Сумма первых и вторых потерь Δσsp1(1) + Δσsp2(2) = 16,8 + 125,16 = 141,96 МПа. Предварительные напряжения с учетом всех потерь: Δσsp2 = σsp – (Δσsp1(1) + Δσsp2(2)) = 560 – 141,96 = 418,04 МПа. Усилие предварительного обжатия бетона с учетом всех потерь: P = σsp2 · Asp = 418,04 · 628 = 262529 H = 262,53 кН. Расчет прочности ребристой плиты по сечению, наклонному к продольной оси. Расчет по бетонной полосе между трещинами Прочность бетонной полосы между наклонными трещинами из условия Q ≤ 0,3Rb · b · h0 = 0,3 · 14,5 · 185 · 360 = 289710 H = = 289,71 кН > Q = 90,84 кН, где Q = Qmax – qh0 = 103,68 – 35,51 · 0,36 = 90,84 кН – поперечная сила в нормальном сечении, принимаем на расстоянии от опоры не менее h0. Прочность бетонной полосы обеспечена. – 25 – Расчет прочности по наклонным сечениям В продольных ребрах устанавливаем каркасы с поперечной арматурой на всю длину ребра. Принимаем диаметр поперечных стержней 6 мм А240 с общей площадью поперечного сечения Asw = 57 мм2 (табл. П15 приложения). Максимальный шаг поперечной арматуры по конструктивным требованиям sw ≤ h0 /2 = 360/2 = 180 мм. Принимаем шаг sw = 150 мм. Прочность по наклонным сечениям проверяем из условия Q ≤ Qb + Qsw, где Q – поперечная сила в конце наклонного сечения; Qb – поперечная сила, воспринимаемая бетоном в наклонном сечении; Qsw – поперечная сила, воспринимаемая поперечной арматурой в наклонном сечении. Усилие в хомутах на единицу длины элемента: q sw = Rsw ⋅ Asw 170 ⋅ 57 = = 64,6 Н/мм (кН/м). Sw 150 Определяем коэффициент φn, учитывающий влияние усилия R ⋅A 170 ⋅ 57 2 q sw = sw sw = = 64,6Р на несущую предварительного обжатия наклонного 262529 2 Р способность 262529 Sw = 1 + 1,6 ϕ n 150 = 1 + 1,6 − 1,16 − 1,16 сечения: 14,5 ⋅ 74000 Rb А1 14,5 ⋅ 74000 Rb А1 2 2 Р Р 262529 262529 = 1 + 1,6 ϕ n = 1 + 1,6 − 1,16 − 1,16 = 1,32. Rb А1 R А 14 , 5 74000 ⋅ 14,5 ⋅ 74000 b 1 A1 = bh = 185 · 400 = 74000 мм2. Хомуты учитываются в расчете, если соблюдается условие qsw ≥ 0,25φnRbt · b = 0,25 · 1,32 · 1,05 · 185 = 64,59 Н/мм < 64,6 Н/мм. Условие выполняется. Поперечная сила, воспринимаемая бетоном М наклонного сечения: 50223726 b с= = = 1510 M q1 22,01 Qb = b , c где Mb = 1,5 φn Rbt bh02 = 1,5 · 1,32 · 1,05 · 185 · 3602 = 50223726 Н·мм, с= Мb 50223726 = = 1510 мм. q1 22,01 M Qb = b , c Если нагрузка включает эквивалентную временную нагрузку, то ее расчётное значение равно – 26 – q1 = q – 0,5qv = 35,51 – 0,5 · 27,0 = 22,01 кН/м, где qv = vbнγп = 18 · 1,5 · 1 = 27,0 кН/м. Проверяем условие 2h0 2 ⋅ 360 = = 823 мм, c> 64,6 q sw 1 − 0,5 1 − 0,5 1,32 ⋅ 1,05 ⋅ 185 ϕ n Rbt b c= Mb . 0,75q sw + q1 условие выполняется, с не пересчитывается. Если условие не выполняется, то с определяется по формуле Mb c= . 2 ⋅ 360 q + q 0 , 75 sw 1 = = 823 мм, 64,6 sw По конструктивным требованиям c ≤ 3h0 = 3 · 360 = 1080 мм. 1 − 0,5 1,32 ⋅ 1,05 ⋅ 185 Rbt b М 50223726 = 46503,5 Н = 46,5 кН, Qb = b = с 1080 при этом Qb не более 2,5Rbtbh0 = 2,5 · 1,05 · 185 · 360 = 174825 Н = 174,825 кН и не менее Qb,min = 0,5φnRbtbh0 = 0,5 · 1,32 · 1,05 · 185 · 360 = = 46153,8 Н = 46,15 кН. Условия выполняются. Определяем усилие: Qsw = 0,75qswc0 = 0,75 · 64,6 · 720 = 34884 Н = 34,9 кН, где с0 =2h0 = 2 · 360 = 720 мм – длина проекции наклонного сечения. Поперечная сила в конце наклонного сечения Q = Qmax – q1c = 103,68 – 22,01 · 1,080 = 79,91 кН. Условие Q ≤ Qb + Qsw; 79,9 < 46,5 + 34,9 = 81,4 кН. Условие выполняется, прочность наклонного сечения обеспечена. Максимально допустимый шаг хомутов, учитываемых в расчете: R ⋅A 170 ⋅ 57 q sw2 = sw sw = ϕ n Rbt bh02 1,32 ⋅ 1,05 ⋅ 185 ⋅ 360 2 Sw 250 s w,max = = = 323 мм. Qmax 103680 Принятый шаг хомутов удовлетворяет требованиям максимально допустимого шага. Принятый шаг хомутов sw1 устанавливается на приопорном участке ребра длиной l1 в зоне максимального значения перерезывающей силы, с уменьшением перерезывающей силы шаг хомутов может быть увеличен до sw2 = 0,75h0 = 0,75 · 360 = 270 мм. – 27 – Принимаем шаг sw2 = 250 мм, при этом усилие в хомутах на единицу длины элемента будет равно Rsw ⋅ Asw 170 ⋅ 57 = = 38,76 Н/мм (кН/м). ⋅ 1,05 ⋅ 185 ⋅ 360 Sw 250 = 323 103680 Длина участка с интенсивностью хомутов qsw1 принимается в зависимости от Δqsw = 0,75(qsw1 – qsw2) = 0,75(64,6 – 38,76) = 19,38 Н/мм M / c + 0,75q sw1c0 − Q max + q1c (кН/м) следующим образом:l1 = c − b = Δq sw − если Δqsw < q1, 19,38 < 22,01 Н/мм q sw2 = 2 50223726 64,+6q⋅1720 ,75q sw+1c00 ,−75Q⋅max M / c + 0/ 1080 c − 103680 + 22,01 ⋅ 1080 = 1080 = 1004 = l1 =−c − b 19,38 Δq sw = 1080 − 50223726 / 1080 + 0,75 ⋅ 64,6 ⋅ 720 − 103680 + 22,01 ⋅ 1080 = 1004 мм; 19,38 c= Mb 50223726 = = 5729,4 мм, q1 − Δq sw 20,91 − 19,38 M b 3h = 3 50223726 но · 360 = 1080 мм, ,принимаем с = 1080 мм. c =не более = 5729 4 o= q q − Δ 20 , 91 − 19 , 38 1 sw При этом, если 2h 2h0 Mb Mb M Mb ; < 0 ; , c= , c= b < q sw +qsw q75 0,275qsw 2 + 0 , q q1 − Δq1sw− Δq sw 1 −q0sw 1 1 ,5 1 − 0,5 φ n Rbt bφ n Rbt b − если Δqsw ≥ q1, − (Q+b1, min + 12,h50q)sw2 h0 ) Qmax −Q(max Qb, min ,5q sw l1 = l1 = − 2h0 .− 2h0 . q1 q1 2.6. Расчет ребристой панели по второй группе предельных состояний Расчет по образованию трещин, нормальных к продольной оси Расчет по образованию трещин выполняют на расчетные усилия при значении коэффициента надежности по нагрузке γf = 1; М = 119,97 кНм. Расчет по раскрытию трещин не производят, если соблюдается условие M ≤ Mcrc, – 28 – d где М – изгибающий момент от внешней нагрузки; Mcrc – изгибающий момент, воспринимаемый нормальным сечением элемента при образовании трещин. Момент образования трещин предварительно напряженных изгибаемых элементов в стадии эксплуатации вычисляют по формуле Mcrc = γWredRbt,ser + P(e0p + r). Mcrc = 1,3 · 8146980 · 1,55 + 262529 · (233,35 + 57,7) = = 92825230 = 92,82 кНм, где Wred – момент сопротивления приведенного сечения для крайнего растянутого волокна, определяемый по формуле W red= 8146980 W I red 2276976941 = 57,7 = = 8146980 см 3 ; r = red = Ared 141182,5 y 273,35 r – расстояние от центра тяжести приведенного сечения до верхней ядровой точки, определяется по формуле = 8146980 W 2276976941 = 57,7 мм; = 8146980 см 3 ; r = red = Ared 141182,5 273,35 γ = 1,3 – коэффициент, учитывающий неупругие деформации бетона (табл. П11 приложения). Так как M = 126,26 > Mcrc = 92,82 кНм – трещины в растянутой зоне образуются. Следовательно, необходим расчет по раскрытию трещин. Расчет по раскрытию трещин, нормальных к продольной оси Расчет по раскрытию трещин производят из условия acrc ≤ acrc,ult, (2.1) где acrc – ширина раскрытия трещин от действия внешней нагрузки; acrc,ult – предельно допустимая ширина раскрытия трещин. Для элементов, к которым не предъявляются требования непроницаемости, значения acrc,ult принимают равными: − при арматуре классов А240…А600, В500: 0,3 мм – при продолжительном раскрытии трещин; 0,4 мм – при непродолжительном раскрытии трещин; − при арматуре классов А800, А1000, а также Вр1200…Вр1400, К1400, К1500 (К-19) и К1500 (К-7) диаметром 12 мм: – 29 – 0,2 мм – при продолжительном раскрытии трещин; 0,3 мм – при непродолжительном раскрытии трещин; − при арматуре классов Вр1500 и К1500 (К-7) диаметром 6 и 9 мм: 0,1 мм – при продолжительном раскрытии трещин; 0,2 мм – при непродолжительном раскрытии трещин. Ширину раскрытия трещин принимают равной: − при продолжительном раскрытии acrc = acrc1; (2.2) − при непродолжительном раскрытии acrc = acrc1 + acrc2 – acrc3, (2.3) где acrc1 – ширина раскрытия трещин, определяемая при φ1 = 1,4 и при действии постоянных и длительных нагрузок (т. е. при М = Ml); acrc2 – то же, при φ1 = 1,0 и действии всех нагрузок (т. е. при М = Mtot); acrc3 – то же, при φ1 = 1,0 и действии постоянных и длительных нагрузок (т. е. при М = Ml). Ширину непродолжительного раскрытия трещин можно также определять по формуле acrc = acrc2(1 + 0,4A), где (2.4) σ sl − 0,8σ s,crc σ ls . , acrc = ϕ1ϕ 2 ψ s s(2.5) Es σ s − 0,8σ s,crc находятся при действии моментов соответсA= а значения σs, σsl, σs,crc твенно Mtot, Ml и Мсrс. При этом, если выполняется условие A > t, можно проверять только продолжительное раскрытие трещин, а если условие не выполняется – только непродолжительное раскрытие. Здесь t = 0,68 – при допустимой ширине продолжительного и непродолжительного раскрытия трещин, равных соответственно 0,3 и 0,4 мм; t = 0,59 – при этих величинах, равных 0,2 и 0,3 мм; t = 0,42 – при этих величинах, равных 0,1 и 0,2 мм. Ширину раскрытия нормальных трещин высчитывают по формуле σ − 0,8σ s,crc σ A = sl , acrc = ϕ1ϕ 2 ψ s s l s . (2.6) Es σ s − 0,8σ s,crc – 30 – b)h'f h0 Пример расчета. Определим приращение напряжения напрягаемой арматуры от действия постоянных и временных длительных нагрузок σs = σsl, т. е. принимая М = Ml = 101,76 кНм. Поскольку напрягаемая арматура в верхней зоне плиты отсутствует, esp = 0,0, Ms = Мl = 107,05 кН·м и тогда es = M s 107,05 = = 0,408 м = 408 мм. P 262,53 es 408 = = 1,13. h0 360 Рабочая высота сечения равна es 408 = = 1,13. h0 360 Принимая A′sp = Asp = 0,0, имеем M 107,05 360 мм. мм, es = s = = 0,408hм0 = 408 P 262,53 ϕf = (b'f − b)h'f = bh0 (1445 − 185)50 = 0,95. 185 ⋅ 360 μas1 = a s1 Asp bh0 = 20,7 ⋅ 628 185 ⋅ 360 Коэффициент приведения равен as1 = 300/Rb,ser = 300/14,5 = 20,7, тогда (1445 − 185)50 = 0,95. = 185 ⋅ 360 μas1 = a s1 Asp bh0 = 20,7 ⋅ 628 = 0,195. 185 ⋅ 360 При es /h0 = 1,13, φf = 0,95 и μas1 = 0,195 из табл. П12 приложения находим ζ = 0,84, тогда плечо внутренней пары сил z = ζ · h0= 0,84·360 = 302,4 мм. M s z − P 107,05 ⋅ 10 6 / 302,4 − 262529 = = 145,66 МПа. Asp M s z628 − P 107,05 ⋅ 10 6 / 302,4 − 262529 σ sl = = = 145,66 МПа. 628 Asp Аналогично определим значение σs,crc при действии момента 92,82кН·м: MS =eМ s crc = 92,82 = = 0,98. h0 262,53 ⋅ 0,36 es 92,82 = = 0,98. h0 262,53 ⋅ 0,36 σsslsl = При es /h0 = 0,98, φf = 0,95 и μas1 = 0,195 из прил. 12 находим ζ = 0,85, тогда плечо внутренней пары сил z = ζ · h0= 0,85·360 = 306 мм. σ crc = M s z − P 92,82 ⋅ 10 6 / 306 − 262529 = = 64,97 МПа. Asp 628 – 31 – Аналогично определим значение σs при действии момента M = Мtot = 126,26 кН·м. Поскольку согласно табл. П12 приложения в данном случае при значении es /h0 > 1 коэффициент ζ не зависит от es /h0, принимаем вычисленное выше значение z = 302,4 мм. При моменте от всех нагрузок МS = Mtat = 126,26 кН·м значение σs равно 6 6 MM ,26 ⋅ 10 / 302 ,4,4− −262529 z −P P 126 126 ,26 ⋅ 10 / 302 262529 s sz − σ sσ = == = =246 ,8,8МПа. 246 МПа. s = 628 Asp 628 Asp Проверим условие принимая = 60,59, M A >z −t, P 126,26 ⋅t10 / 302,4 − 262529 σs = s = = 246,8 МПа. σσ − − 0,08,σ8s,σcrc 145 ,66 −− 0,08,⋅864 ,97 145 ,66 ⋅ 64 ,97628 s,crcAsp A A= = sl sl == = =0,048 , , ,48< <t =t =0,059 ,59 σ sσ−s − 0,08,σ8s,σcrc ,8,− 0,08,⋅864 ,97 246 8− ⋅ 64 ,97 s,crc 246 σs = A= 0,8σширину M s z −следовательно, P 126,26 ⋅ 10 6 определяем раскры/ 302σ,4 −−262529 145непродолжительного ,66 − 0,8 ⋅ 64,97 s,crc = ==246,8 МПа. A = sl = 0,48 < t = 0,59, σ A σ A 64 , 97 64 , 97 тия трещин. 628σs,crc Asp 246 − .0,8l ⋅l64 s − 0,97 ,05,5 bt btd sd,s , ψψ 1 −1 −0,08,8 s,crc = 01=,−18σ−0,s,08crc = =0,8,079 ,8 ,79. s = s = s = s = Asp Asp Находим коэффициент ψs, принимая σs = 246,8 МПа: σ sσ s 246 ,8,8 246 A σ sl − 0,8σ s,crc 145,66 − 0,8 ⋅ 64,97 σ s,crc 64,97 ψ s = 1 − 0,8= 0,48 <=t1=− 0,59 8 , = 0,79. l s = 0,5 bt d s , = Asp σs 246,8 σ s − 0,8σ s,crc 246,8 − 0,8 ⋅ 64,97 Рассчитываем расстояния между трещинами ls по формуле ψ s = 1 − 0,8 σ s,crc A 64,97 = 1 − 0,8 = 0,79. l s = 0,5 bt d s , Asp σs 246,8 где Abt – площадь зоны растянутого бетона. Высота зоны растянутого бетона, определенная как для упругого материала, при Sred = 38592299,2 мм3 равна y0 = Ared S red 38592299,2 = = 124,27 мм, + P / Rbt , ser 141182,5 + 262529 / 1,55 а с учетом неупругих деформаций растянутого бетона A 21839,25 l s = 0,5 bt ydt s==k0·,5y0 = 0,95 · 124,27 20 = 348 = мм. 118,05 мм. Asp 628 Поскольку yt > 2а = 2 · 40 = 80 мм, принимаем yt = 118,05 мм. Тогда площадь сечения бетона равна σ s растянутого 246,838592299 acrc, 2 = ϕ1ϕ l s S=red0,5 ⋅ 0,79=⋅ ⋅ 348 = 20,,2169 мм.= 124,27 мм, ==s by = yA02 ψ 185 · 118,05 = 21839,25 мм , / 1,55 E 200000 bt Aredst + P / Rbt , ser 141182,5 + 262529 и расстояние между трещинами равно A 21839,25 l s = 0,5 bt d s = 0,5 20 = 348 мм. Asp 628 σ 246,8 acrc, 2 = ϕ1ϕ 2 ψ s –s 32 l s =–0,5 ⋅ 0,79 ⋅ ⋅ 348 = 0,169 мм. Es 200000 y0 = S red 38592299,2 = = 124,27 мм, Ared + P / Rbt , ser 141182,5 + 262529 / 1,55 Поскольку ls < 400мм и ls < 40d = 40 · 20 = 800 мм, принимаем Abt 21839,25 d s = 0,5 20 = 348 мм. ls = 348lмм. s = 0,5 Asp 628 Определяем ширину раскрытия acrc,2, принимая φ1 = 1,0, φ2 =0,5 acrc, 2 = ϕ1ϕ 2 ψ s σs 246,8 l s = 0,5 ⋅ 0,79 ⋅ ⋅ 348 = 0,169 мм. Es 200000 Определяем непродолжительное раскрытие трещин acrc = acrc,2(1 + 0,4A) = 0,169(1 + 0,4 · 0,4) = 0,196 мм, что меньше предельно допустимого значения 0,3 мм. Расчет прогиба плиты Расчет изгибаемых элементов по прогибам производят из условия f ≤ fult, (2.7) где f – прогиб элемента от действия внешней нагрузки; fult – значение предельно допустимого прогиба. Прогиб плиты ограничивается эстетическими требованиями. Для элементов постоянного сечения, работающих как свободно опертые или консольные балки, прогиб допускается определять, вычисляя кривизну только для наиболее напряженного сечения и принимая для остальных сечений кривизны, изменяющиеся пропорционально значениям изгибающего момента, т. е. по формуле 1 r max где 1 M 1 1 1 (2.8) f = Sl 2 , = , = − r Eb1 I red E = Eb r max r r 1 b1 1 + ϕb,cr – полная кривизна в сечении с наибольшим изгибающим моментом; S – коэффициент, принимаемый по прил. 14. Полную кривизну изгибаемых элементов определяют: 1) для участков без трещин в растянутой зоне по формуле 1 1 1 1 = + − r r 1 r 2 r 3 , (2.9) 1 1 где и – кривизны соответственно от непродолжитель r 1 r 2 ного действия кратковременных нагрузок и от продолжительного 1 r 3 действия постоянных и длительных нагрузок; – кривизна от – 33 – непродолжительного действия усилия предварительного обжатия Р (т. е. при действии M = Peop). Кривизну элемента на участке без трещин определяют по формуле 1 M (2.10) , = r Eb1 I red где М – изгибающий момент от внешней нагрузки или момент усилия предварительного обжатия относительно оси, проходящей через центр тяжести приведенного сечения; Ired – момент инерции приведенного сечения относительно его центра тяжести, определяемый как для сплошного тела по общим правилам сопротивления упругих материалов с учетом всей площади бетона и площадей сечения арматуры с коэффициентом приведения арматуры к бетону, равным а = Es /Eb1; Eb1 – модуль деформации сжатого бетона, принимаемый равным: − при непродолжительном действии нагрузки Eb1 = 0,85Eb; (2.11) действии нагрузки 1 M 1−при продолжительном 1 1 1 1 f = Sl 2 , = , = − + E r Eb1 I red E = b r max r r 1 r 2 r (2.12) 3 ; b1 1 + ϕb,cr 2) для участков с трещинами в растянутой зоне по формуле 1 1 1 1 (2.13) = − + , r r 1 r 2 r 3 1 где – кривизна от непродолжительного действия всех нагрузок, r 1 1 на которые производят расчет по деформациям; – кривизна от r 2 непродолжительного действия постоянных и длительных нагрузок; 1 – кривизна от продолжительного действия постоянных и дли r 3 тельных нагрузок. Кроме того, в формулах (2.9) и (2.13) может быть учтена кривиз1 на , обусловленная остаточным выгибом элемента вследствие r 4 усадки и ползучести бетона в стадии изготовления от усилия пред- – 34 – варительного обжатия Р(1) и собственного веса элемента. Значение 1 рассчитывается по формуле r 4 σ − σ 'sb 1 , = sb Es h0 r 4 1 M es , (2.14) = = 0,98 3 r ϕc bh0 Eb,red h0 где σsb и σ′sb – значения, численно равные сумме потерь предварительного напряжения арматуры от усадки и ползучести бетона соответственно для арматуры растянутой зоны и для арматуры, условно расположенной на уровне крайнего сжатого волокна бетона. Для сечений при h′f ≤ 0,3h0 и a′s < 0,2h0 кривизну допускается вычислять по формуле ' σ − σ sb 1 M e 1 , s = 0,98 = , = sb (2.15) 3 r ϕc bh0 Eb,red h0 Es h0 r 4 где φс – коэффициент, определяемый по табл. П13 приложения в зависимости от φf, μas2, es /h0. 1 Пример расчета. Определяем кривизну в середине пролета от r продолжительного действия постоянных и длительных нагрузок, т. е. при М = Ml = 107,05 кН·м. σ − σ' 1 M e 1 этих имеем:, s = 0,98 , φf = 0,95, ψs = 0,79. = , нагрузок = sbДля sb 3 r ϕc bh0 Eb,red h0 Es h0 r 4 При продолжительном действии нагрузки и нормальной влаж- Rb, ser Es 200000 18,5 -4 = 38,32; = = 6607 МПа. aεsb1,red 2 = = 28 × 10= при −4 ψ s Eb,red 0,79 ⋅ 6607 еb1, red 28 ⋅ 10 влажности окружающей среды 70 ≥ W ≥ 40 %. Es 200000 18,5 Тогда AEspb, red = Rb, ser 628= = = 6607 МПа. a s 2 = − 4 Rb, ser μ a = a = 38 , 32 = 0 , 36 . 200000 18,5 ψ s Eb,red 0,79 ⋅ 6607 s2 s 2 еbE s 1, red =28 ⋅ 10 = 38,32; = = 6607 МПа. bha s 2 = 185 ⋅ 360 E 0 , 79 ⋅ 6607 еb1, red 28 ⋅ 10− 4 Rb, ser 0 18ψ Es 200000 ,5s b,red = = 38,32; Eb, red = = = 6607 МПа. a s 2 = −4 E ψ 0 , 79 ⋅ 6607 еb1, red 28 ⋅ 10 Asp 628 6 s b,red 1 1 μas 2 = M as 2 = 101,76 ⋅10 0,36. = = =185 ⋅ 360 38,32 = = 2,93 ⋅10 −6 1/мм. 628 sp bh 3 r . 3 ϕc bh0 0Eb,red 0,61 ⋅185 ⋅ 3603 ⋅ 6607 as 2 = 38,32r= 0,36 Asp h0 185 ⋅ 360 По табл. 628 es /h0 = 0,98 и μαs2 = 0,36 μas 2 = П13 as 2 приложения = 38,при 32 =φ0f,= 360,95, . 6 bh 185 ⋅ 360 1 σ 1 125 , 16 M = 1,74 1 кривизна находимφc =0 0,61. Тогда равна = 1 sb ⋅ 10 − 6 101,76 ⋅10 = = 2,93 ⋅10 −6 1/мм. 6= = = 5 3 r 3 r ,476 ⋅10 Ers h0 r 23⋅ 10ϕ ⋅bh M 360 101 6 red c ⋅10 0 E−b, = = = 2,93 1/мм.0,61 ⋅185 ⋅ 360 ⋅ 6607 3 101,76 ⋅10 6 ϕc bh03 Eb,red 10,61 ⋅1185 6607 ⋅ 360 ⋅ M = = 1 13 σ 1= = 2,93 ⋅10 −-661/мм. 125 ,16 3 -6 sb 0,= r r 1 3 ϕ= 61 ⋅ 185 ⋅ 360 ⋅ 6607 bh E ( 2 , 93 − 1 , 74 ) ⋅ 10 =− 61,19 ⋅10 1/мм. − = = = 1 , 74 ⋅ 10 c 0 b,red 5 σ sb 125,16 r r r max r E h = = 1,74 ⋅ 10 − 6 4 3 s 0 4 2 ⋅ 10 ⋅ 360 E s h0 2 ⋅ 105 ⋅ 360 1 σ 125,16 −6 = sb = 1 5 1 = 1,74 1 ⋅510 35 – – ⋅ 360 r 4 E sh10 2⋅ 10 2 − 6 = (2,932 =−41,,22 74)мм. ⋅10 -6 = 1,19 ⋅10 -6 1/мм. − = ⋅10 ⋅ ⋅ 5840 f = -r6 Sl = 1,19 1 1 r r 4. 3-6 1/мм 48 max max = 1,19 ⋅10 = − = (2,93 − 1,74)r⋅10 r 3 r 4 1 1 1 -6 -6 ности Eb, red = s 38,32 =a s02,36 Rb, seras 2 −=4 18 200000 =. =E s = 38,32; 5 2 == Eb, red = μabs, ser = ,6607 МПа. a ss2E= = 38 Ebе,bred = bh = 185 ⋅−360 = 6607 МПа. ψ 0,79=⋅ 6607 0 ⋅ 10 28 4 b,red 1, red ψ s Eb,red 0,79 ⋅ 6607 еb1, red 28 ⋅ 10 1 M 1 101,76 ⋅10 6 Asp 628 = 2,93при ⋅10 −6 1/мм. Определим выгибом μas 2 = r =кривизну, asr2A=sp = обусловленную 38,32 == 0,36.остаточным 3 628 3 ,61=⋅185 ⋅ 6607 bh0 Eb,red 380,32 μbh as02 = 3 185 asϕ 0,36⋅ 360 . 360 2 ⋅c= σsb = 125,16 МПа. bh 185 ⋅ 360 0 σ sb 125,16 1 = 1,74 ⋅610 − 6 1/мм, 1 1 r = EMh = 5 101,76 ⋅10 2=⋅ 10 ⋅ 360 101,76 ⋅10 6= 2,93 ⋅10 −6 1/мм. = 1 =14 3s 0 M = = = 2,93 ⋅10 −6 1/мм. r r r 3 rϕcравны 61= ⋅185напряжений ⋅ 3603 ⋅ 66073 от усадки bh E red 3 0,потерь где σsb – численно сумме и пол 3 0 ϕb,c bh 0 , 61 ⋅ 185 ⋅ 360 ⋅ 6607 E 0 b,red 1 = 125,16 МПа. 1 σ = 40 1+85,16 -6 -6 зучести бетона, ,16− = (2,93− 6− 1,74) ⋅10 = 1,19 ⋅10 1/мм. σ sb sb = 125 1 r r r σ 1 125 , 16 = = = 1 , 74 ⋅ 10 max 3 4 Полная кривизнаsbв середине пролета от постоянных и длитель= 1,74 ⋅ 10 − 6 r 4 rEs h0= E2h⋅ 10=5 ⋅ 360 5 ных нагрузок 2 ⋅ 10 ⋅ 360 равна 4 s 0 5 1 2 1 f =1 − 11Sl 2 == 1(1,219 ⋅ 10−−16,74 ⋅ ) ⋅10 ⋅ 5840 4,22 -6 -6 1 , 93 = =1-,619 ⋅10мм. 1/мм. = − r= max 48 = ( 2 , 93 − 1 , 74 ) ⋅ 10 = 1 ,19 ⋅10 -6 1/мм. r r r max r 3 r 4 r max 3 4 Прогиб плиты находим, принимая S = 5/48: 5 1 5 2 = 4,22 f = Sl1 2 = 1,192 ⋅ 10 −6 ⋅ −⋅ 65840 мм. f Sl = 1 , 19 ⋅ 10 ⋅ ⋅ 5840 2 = 4,22 мм. = 48 r max r 48 max Согласно СП 20.13330.2011 «Нагрузки и воздействия» поз. 2 при l = 5,84 м предельно допустимый из эстетических требований прогиб равен fult = 5840/200 = 29,2 мм, что превышает вычисленное значение прогиба. 2.7. Конструкция типовой ребристой плиты перекрытия В разделе представлены чертежи ребристой плиты перекрытия размером 1,5×6,0 м для опирания на нижние полки ригеля из серии 1.442.1–1.87 «Плиты перекрытий железобетонные ребристые высотой 400 мм, укладываемые на полки ригелей». Конструктивная ширина панели 1485 мм, длина – 5550 мм. На рис. 2.1 и 2.2 приведены геометрические размеры панели. Армирование панели изображено на рис. 2.6–2.9. – 36 – Рис. 2.6. Армирование панели: 1 – сетка усиления зоны передачи напряжений на концевых участках ребер; 2 – каркас с поперечной арматурой продольного ребра; 3 – плоский каркас поперечного ребра; 4 – плоский каркас торцевого ребра; 5 – сетка армирования полки, воспринимающая опорный отрицательный момент; 6 – сетка армирования полки, воспринимающая пролетный момент и опорный момент над поперечным ребром; 7 – опорная закладная деталь со строповочной петлей; 8 – продольная напрягаемая арматура Рис. 2.7. Узел I, армирование (обозначение см. рис. 2.6) – 37 – Рис. 2.8. Узел А1, армирование (обозначение см. рис. 2.6) Рис. 2.9. Узел II, армирование (обозначение см. рис. 2.6) – 38 – 3. ПРОЕКТИРОВАНИЕ ПУСТОТНОЙ ПАНЕЛИ ПЕРЕКРЫТИЯ 3.1. Конструкция типовой пустотной панели Конструктивные параметры поперечного сечения пустотной плиты номинальной ширины 1,5 м приведены на рис. 3.1: − высота сечения – 220 мм; − конструктивная ширина – 1490 мм; − рабочая высота сечения: h0 = h – aр = 220 – 30 = 190 мм; − ширина нижней полки: bf =1490 мм; − ширина верхней полки: b′f = 1490 – 2 · 15 = 1460 мм. Рис. 3.1. Конструкция пустотной панели Рис. 3.2. Расчетное сечение пустотной панели – 39 – В расчетах по предельным состояниям первой группы сечение панели приводится к двутавровому с параметрами (рис. 3.2): − толщина полок h′f = hf = (h – d)/2 = (220 – 159)/2 = 30,5 мм; − ширина ребра b′f + b f 1460 + 1490 − 7 ⋅ 159 = 362 мм. 2 2 Отношение h′f /h = 30,5/220 = 0,139 > 0,1, в расчет вводится вся ширина верхней полки b′f = 1460 мм. b= − nd = 3.2. Расчетный пролет, нагрузки и усилия в плите Подсчет нагрузок на 1 м2 перекрытия приведен в табл. 2. Таблица 2 2 Нормативные и расчетные нагрузки на 1 м перекрытия № п/п КоэфРасНормативфициент четные ные нагрузнадёжности нагрузки, ки, кН/м2 по нагрузке кН/м2 Вид нагрузки Постоянные Собственный вес плиты с залив1. кой швов 2. Конструкция пола: керамическая плитка на цементно-песчаном растворе δ = 20 мм 18 × 0,02 × 1 = 0,36 армированная цементно-песчаная стяжка δ = 35 мм 20 × 0,035 × 1 = 0,70 песчаная засыпка δ = 70 мм 17 × 0,07 × 1 = 1,19 Итого постоянная 3,3 1,1 3,63 0,36 1,3 0,468 0,70 1,3 0,91 1,19 1,3 1,547 5,55 3. Временная в том числе кратковременная 4. Полная в том числе постоянная и временная длительная нагрузки – 40 – 6,555 8 1,2 3 1,2 9,6 3,6 13,55 16,455 10,55 12,555 Расчетная нагрузка на 1 п. м плиты при ее номинальной ширине 1,5 м с учетом коэффициента надежности по ответственности здания γп = 1,0: − полная расчетная q = 16,455 · 1,50 · 1,0 = 24,68 кН/м; − полная нормативная qn = 13,55 · 1,5 · 1,0 = 20,33 кН/м; − постоянная и временная длительная нормативные нагрузки ql = 10,55 · 1,50 · 1,0 = 15,82 кН/м. Усилия от расчетных и нормативных нагрузок Расчетный пролет плиты при ее конструктивной длине 5,98 м bриг 0,3 м. − f = 6,0 − − 0,01 = 5,84 м. 2 2 Плита рассчитывается как однопролетная шарнирно-опертая q ⋅ 20 24,68 ⋅ распределенной 5,84 2 q ⋅ 0 24,68 ⋅ 5,84 балка, загруженная М = равномерно =bриг =0105 ,3 ,21 Qнагрузкой. = = = 72,07 = − − f = 6 , 0 − − 0 , 01 = 5 , 84 8 8 2м. 2 0 2 расчетной нагрузки: Усилия от полной 2 2 − максимальный изгибающий момент в середине пролета2 q ⋅ 15,82 ⋅ 5,84 2 q n ⋅ 220 20,33 ⋅ 5,84 22 q ⋅ 24 , 68 ⋅ 5,84 = 86,63 M l = q l⋅ 00 =24,68 ⋅ 5,84 = 67,37 Mn = bриг 0 = 0,3 = = 105,21 кН·м; Q= 8 = = 72,07 8 8 2 − − f = 6,0 − − 0,01М = 5=,8488м.bриг 0,3 8 2 2 2 0 = 2 − − f = 6,0 − − 0,01 = 5,84 м.2 − максимальная поперечная 2 сила на опорах 2 2 2 2 2 ql ⋅ 20 15,82 ⋅ 5,84 2 qqn⋅ ⋅ 0 24 20,68 ,33⋅⋅55,,84 84 q ⋅ 0 24,68 ⋅ 5,84 0 = = = 67,3 M M = = = 86 , 63 = = 105,21 Qn =q ⋅ 2 =24,68 ⋅ 5,84 2 = 72,07 кН. l q ⋅ 24,68 ⋅ 58,84 b8риг 08 8 0,3 280 = 28 М = = 105 , 21 Q= = = 72,07 − − f = 6,0 − − 0,01 = 5,84 м. 8 8 2 2 Усилия от нормативной нагрузки: 2 2 ql ⋅ 20 15,82 ⋅ 5,84 2 q ⋅ 2 20,33 5,84 2 − ⋅полной 2 = =20,33 ⋅ 5,84 2 = 67,37 M = 2n 0 = = 86 , 63 l 2 ql ⋅ 20 15,82 ⋅ 5,84 2 0 8 24,68 ⋅ 5,84 q ⋅qn ⋅ 8024,68 8 ⋅ 5,848 = = = 67,3 M = 86 , 63 кН·м; l = = 105,21 QM=n = 08= = = 72,07 8 8 8 8 2 2 8 − постоянной и временной длительной n 0 = 2 − q ⋅ 2 15,82 ⋅ 5,84 2 ⋅ 20 20,33 ⋅ 5,84 2 = 67,37 кН·м. = = 86,63 M l = l 0 = 8 8 8 8 3.3. Характеристики прочности бетона и арматуры Многопустотная предварительно напряженная плита армирована стержневой арматурой класса А800 с механическим натяжением на борта формы. Нормативное сопротивление арматуры Rsn = 800 МПа, расчетное сопротивление Rs = 695 МПа; модуль упругости Es = 200000 МПа. Поперечная арматура класса В500 – 41 – h02 с расчетным сопротивлением Rsw = 300 МПа (табл. П4, П5, П6, П7 приложения). Изделие подвергают тепловой обработке при атмосферном давлении. Величина предварительного напряжения арматуры принята равной σsp = 0,7Rsn = 0,7 · 800 = 560 МПа. Бетон тяжелый класса В25, соответствующий классу напрягаемой арматуры. Расчетные сопротивления бетона для расчета по первой группе предельных состояний: Rb = 14,5 МПа; Rbt = 1,05 МПа. Расчетные сопротивления бетона для расчета по второй группе предельных состояний: Rb,ser = 18,5 МПа; Rbt,ser = 1,4 МПа. Начальный модуль упругости бетона Еb = 30000 МПа (табл. П1, П2, П3 приложения). 3.4. Расчет пустотной панели по первой группе предельных состояний Расчет прочности плиты по нормальному сечению Расчетный изгибающий момент М = 105,21 кН·м. Сечение двутавровое с полкой в сжатой зоне. Предполагаем, что нижняя граница сжатой зоны бетона проходит в верхней полке, и сечение рассчитываем как прямоугольное с шириной, равной ширине верхней полки. Вычисляем коэффициент αm: mm 6 105 M 105,21 ,2110 10 6 0,138. M 2 0,138. RRbbbbff hh0202 14 14,5,51460 1460190 190 2 6 высота сжатой зоны бетона: 105,21 10Относительная 0,138. 2 11 1122mm 11 112200,138 14,5 1460 190 ,149190 19028 2 ,13800,149 ,149.. xxhh00 00,149 Высота сжатой зоны бетона: m 1 1 2 0,138 0,149. x h0 0,149 190 28,25 мм. Так как x < h′f, то нейтральная ось проходит в полке. Граничная высота сжатой зоны бетона (табл. П10 приложения): ξR = 1+ 0,8 = Rs + 400 − σ sp 700 0,8 = 0,42. 695 + 400 − 560 1+ 700 Так как ξ < ξR, установка арматуры в сжатой зоне не требуется. – 42 – 0,8 400 sp 700 x s 0,8 0,42. 800 400 560 1 1 700 700 Площадь продольной рабочей арматуры равна 0,8 0,42. sp 560 800 400 560Rb bf x 14,5 1460 28,25 1 0,81 0,6 AS 782,5 мм 2 , 700 s 3 Rs 1,1 695 Rs 695 0,8 Rsn 400 sp R где γs = 1,1, так как 14,5 1460 28,25 782,5 мм 2 , 1,1 695 sp Rs 560 0,81 0,6. 695 Принимаем арматуру 8∅12 мм с Аs = 905 мм2. Геометрические характеристики приведенного сечения Коэффициент приведения E 200000 s 6,67. 30000 E b Es 200000 6,67. Площадь бетонного сечения. Для этого сечение разбиваем на Eb 30000 три участка – ребро и свесы A b (рис. h (b3.3). f b)h f (b f b) h f 362 220 (1460 362) 3 30,5 мм 2 . A b h (b f b)h f (b f b)h f 362 220 (362 1460 (1490 ) 30362 ,5 ) 147533 (1490 362) 30,5 147533 мм 2 . Ared A Asp 147533 6,67 905 153569,35 мм 2 . Ared A Asp 147533 6,67 905 153569,35 мм 2 . Es 200000 6,67. Eb 30000 A b h (b f b)h f (b f b)h f 362 220 (1460 362) 30,5 Рис. 3.3. Схема сечения для определения геометрических характеристик сечения приведенного (1490 362) 30 ,5 147533 мм 2 . Площадь приведенного сечения: Ared Aspsp 147533 6,67 905 153569,35 мм 2 . Ared = AA+aA Статический момент площади приведенного сечения относительно нижней грани: Sred ( Ai yi ) 362 220 110 (1460 362)30,5 204,75 (1490 362)30,5 15,25 6,67 905 30 16323024,25 мм3 , y S red 16323024,25 – 43 106 ,29–мм. 153569,35 Ared i сечения; red i где Аi – площадь i-го участка yi – расстояние от нижней S A y 204 ( ) 362 220 110 ( 1460 362 ) 30 , 5 75 905 30 16323024,25 мм3 , ( 1490 362 ) 30 , 5 15 , 25 6,,67 red i i грани до центра тяжести i-го участка сечения. (1490 362)30,5 15 6,67 905 30 до 16323024 ,25приведенного мм3 , Расстояние от,25 нижней грани центра сечения: 16323024,25 S 106,29 мм. y red 16323024,25 S Ared 106 y red ,29 мм.153569,35 S Ared ( A y ) 362 220 110 (1460 362)30,5 204,75 153569,35 Момент инерции приведенного сечения: 3 362 220 2 362 2203 yi()106 ] 362 220 (106,29 362 ,29 110) 2 [ I i A I red [ I i Ai ( y yi ) 2I]red i ( y 220 12 12 30,53 (1460 362) 30,53 (1490 362) 2 30,53362 (1460 30,5 362 204,75 )362 1460 (106),29 1460 30,5 (106,29 204,75) 2 30,5 12 12 12 (1490 362) 30,5 (106,29 15,25) 2 6,67 905 (106,29 30) 2 2 974566071,8 мм 4 , (1490 362) 30,5 (106,29 15,25) 6,67 905 (106,29 30) 2 где Ii – собственный момент инерции i-го участка сечения. Потери предварительного напряжения в арматуре Первые потери предварительного напряжения: − потери от релаксации напряжений в арматуре при электротермическом способе натяжения Δσsp1 = 0,03σsp = 0,03 · 560 = 16,8 МПа. Для арматуры класса А540 – Δσsp1 = 0,0; − потери от температурного перепада между натянутой арматурой и упорами Δσsp2 = 0. Потери от деформации формы Δσsp3 и анкеров Δσsp4 при электротермическом натяжении арматуры равны нулю. Усилия обжатия с учетом первых потерь: Р(1) = Asp · (σsp – Δσsp(1)) = 905 · (560 – 16,8) = 491600 H = 491,6 кН. В связи с отсутствием напрягаемой арматуры в сжатой зоне бетона (A′sp = 0) эксцентриситет будет равен e0p(1) = ysp = y – ap = 106,29 – 30 = 76,29 мм. Максимальное сжимающее напряжение бетона σbp при обжатии с учетом первых потерь от силы Р(1): bp P(1) Ared sp 6 P(1) e0 p1 y I red 491600 491600 76,29 106,29 7,3 МПа. 153369,35 974566071,8 bр44 – 0,8b,cr – еop1 y s Ared 1 sp (1 )(1 0,8b,cr ) I red Условие σbp ≤ 0,9Rbp = P 0,9 выполняется, P(1)= e15,75 491600где 76,29 106,29 (1) · 17,5 0 p1 yМПа491600 bp Rbp = 0,7В = 0,7 · 25 = 17,5 МПа. Ared I red 153369,35 974566071,8 Вторые потери предварительного напряжения: − потери от усадки: ,bр 0,876 P(1) P(1) e0 p1 y b,cr 491600 491600 ,29 106 29 bp Δσ = e sp 6 = 0,0002· 200000 = 40 МПа; 7,3 МПа. · E еop1 y s A sp5 s Ared I red b,sh 153369 ,35 974566071 ,8red 1 sp (1 )(1 0,8b,cr ) − потери от ползучести: I red 0,8 2,5 6,67 4,46 0,8b,cr bр sp 6 76,29 106,29 153369,35 еop11 y6s,67 Ared 0 , 00613 ( 1 )( 1 0 , 8 2 , 5 ) 1 sp (1 )(1 0,8b,cr ) 974566071,8 I red 0,8 2,5 6,67 4,46 46,5 МПа; 76,29 106,29 153369,35 1 6,67 0,00613 (1 )(1 0,8 2,5) 974566071,8 Asp 905 0,00613, A 147533 где φb,cr – коэффициент ползучести бетона (табл. П4 приложения); Asp 905 0,00613, в бетоне на уровне напрягаемой армаα= Es /Eb; σbp – напряжение A 147533 туры с учетом собственного веса плиты. Напряжение в бетоне на уровне напрягаемой арматуры с учетом собственного веса плиты: (y1)sp e0 pM P(1) P(1P gyy s M491600 y ) (1)e0 p1 P 1 sp g s 491600 bp Ared 153369 AredI red I red I red I red ,35 153369,35 491600 76 ,29 76 ,29,29 21 ,44 10 6 76,29 6 491600 76 ,29 76,29 21,44 10 476 ,46 МПа 4,46 МПа , 974566071 ,8 ,8 974566071 ,8 974566071 974566071 ,8 bp здесь Mg – момент от собственного веса плиты, установленной на деревянные прокладки, Mg 2 qw 2 5,q35 25,665,35 5,662 м, M g w 21,44 кН 21,44 кН м, 8 88 8 где qw = 3,3 · 1,475 · 1,1 = 5,35 кН/м – погонная нагрузка от собственного веса плиты; ℓ – расстояние между деревянными опорными прокладками. Сумма вторых потерь Δσsp(2) = Δσsp5 + Δσsp6 = 40 + 46,5 = 86,5 МПа. – 45 – Сумма первых и вторых потерь Δσsp1(1)+ Δσsp2(2) = 16,8 + 86,5 = 103,3 МПа. Предварительные напряжения с учетом всех потерь Δσsp2 = σsp – (Δσsp1(1) + Δσsp2(2)) = 560 – 103,3 = 456,7 МПа. Усилия предварительного обжатия бетона с учетом всех потерь: Р = σsp2 · Asp = 456,7 · 905 = 413313,5 H = 413,3 кН. Расчет прочности пустотной плиты по сечению, наклонному к продольной оси. Расчёт пустотной плиты по бетонной полосе между трещинами Прочность бетонной полосы между наклонными трещинами определяют из условия Q ≤ 0,3Rb · b · h0 = 0,3 · 14,5 · 362 · 190 = 299193 H = = 299,2 кH > Q = 67,38 кН, Q = Qmax – qh0 = 72,07 – 24,68 · 0,19 = 67,38 КН – поперечная сила в нормальном сечении, принимаем на расстоянии от опоры не менее h0. Прочность бетонной полосы обеспечена. В продольных ребрах между пустотами устанавливаем четыре каркаса с поперечной арматурой класса В500. Принимаем диаметр поперечных стержней 4 мм с общей площадью Asw = 50,2 мм2. Максимальный шаг поперечной арматуры по конструктивным требованиям sw ≤ h0 /2 = 190/2 = 95 мм. Принимаем шаг поперечных стержней sw = 90 мм. Расчет пустотной панели по наклонным сечениям Прочность по наклонным сечениям проверяем из условия Q ≤ Qb + Qsw, где Q – поперечная сила в конце наклонного сечения; Qb – поперечная сила, воспринимаемая бетоном в наклонном сечении; Qsw – поперечная сила, воспринимаемая поперечной арматурой в наклонном сечении. Усилие в хомутах на единицу длины элемента q sw Rsw Asw 300 50,2 167,3 Н/мм (кН/м). Sw 90 2 n 1 1,6 Р Р 413310 413310 – 1 1,6 1,– 1,16 1646 Rb А1 R А 14 , 5 79640 14,5 79640 b 1 2 Определяем коэффициент φ , учитывающий влияние усилия n R A 300 50,2 q sw sw sw 167,3на несущую способность наклонного предварительного обжатия Sw 90 сечения: 2 n 1 1,6 2 Р Р 413310 413310 1 1,6 1,16 1,16 1,42 , Rb А1 14,5 79640 14,5 79640 Rb А1 где A1 = bh = 362 · 220 = 79640 мм2. Мb 29741589 ,7 Хомутыс учитываются в расчете, если соблюдается условие 1304 Mb q1 17,48 , R · b = 0,25 · 1,42 · 1,05 · 362 = 137,3 Н/мм < 167,3 Н/мм. qQswb ≥ 0,25φ c nR bt A 300 50,2 q sw sw sw 167,3 Условие выполняется. Sw 90 Поперечная сила, воспринимаемая бетоном наклонного сечения: 2 2 Q Р Рb = M b , 413310 413310 n 1 1,6 1,16 c 1 1,6 14,5 79640 1,16 14,5 79640 1,42 Rb А1 Rb А1 2 где Mb = 1,5φn Rbt bh0 = 1,5 · 1,42 · 1,05 · 362 · 1902 = 29741589,7 Н·мм, Мb 29741589,7 с 1304 мм. Mb q1 17,48 Qb , c Если нагрузка включает эквивалентную временную нагрузку, то ее расчётное значение равно q1 = q – 0,5qv = 24,68 – 0,5 · 14,4 = 17,48 кН/м, где qv = vbнgn = 9,6 · 1,5 · 1,0 = 14,4 кН/м. Проверяем условие 2h0 2 190 c 557,2 мм. q sw 167,3 1 0,5 1 0,5 1,42 1,05 362 n Rbt b c Условие выполняется, с не пересчитывается. Если условие не выполняется, то с определяется по формуле Mb c . 2 190 q q 0 , 75 sw 1 557,2 мм. 167,3 1 0,5 По конструктивным требованиям c ≤ 3h0 = 3 ⋅ 190 = 570 мм. 1,42 1,05 362 b М 29741589,7 Qb = b = = 52178,2 Н = 52,18 кН, 570 с при этом Qb не более Qmax = 2,5Rbt bh0 = 2,5 · 1,05 · 362 · 190 = 180547,5 Н = 180,55 кН и не менее – 47 – Mb . 0,75q sw q1 Qb,min = 0,5φn Rbt bh0 = 0,5 · 1,42 · 1,05 · 362 · 190 = 52178 Н = 52,18 кН. Условия выполняются. Определяем усилие: Qsw = 0,75qsw c0 = 0,75 · 167,3 · 380 = 47680,5 Н = 47,68 кН, где с0 =2h0 = 2 · 190 = 380 мм – длина проекции наклонного сечения. Поперечная сила в конце наклонного сечения: Q = Qmax – q1c = 72,07 – 17,48 · 0,57 = 62,11 кН. Условие Q ≤ Qb + Qsw, 62,11 < 52,18 + 47,68 = 99,86 кН. Условие выполняется, прочность наклонного сечения обеспечена. Максимально допустимый шаг хомутов, учитываемых в расчете: s w,max n Rbt bh02 1,42 1,05 362 190 2 270,3 мм. Qmax 72070 Принятый шаг хомутов удовлетворяет требованиям максимальQmax Qb 72,07 52,18 но допустимого 0,81 l1 шага. q 24,68 Каркасы с принятым шагом хомутов sw устанавливаются на приопорном участке панели длиной l1, где поперечная сила восприни2 мается бетоном и поперечной В 2середине ребра, R bhарматурой 362 190 1,42 1,05ребра. s w,max n bt 0 270,3 где поперечная сила воспринимается бетоном, Qmax 72070 поперечную арматуру не устанавливают: l1 Qmax Qb 72,07 52,18 0,81 м. q 24,68 3.5. Расчет пустотной панели по второй группе предельных состояний Расчет по образованию трещин, нормальных к продольной оси Расчет по образованию трещин выполняют на усилия при значении коэффициента надежности по нагрузке γf = 1; М = 82,32 кН∙м. Расчет по раскрытию трещин не производится, если соблюдается условие М ≤ Mcrc. Для предварительно напряженных элементов в стадии эксплуатации момент образования трещин предварительно напряженных изгибаемых элементов в стадии эксплуатации определяют по формуле Mcrc = γWred Rbt,ser + P(e0p + r); – 48 – Mcrc = 1,25 ∙ 9168934,7 ∙ 1,55 + 413310 ∙ (76,29 + 59,78) = = 74003902,7 = 74,0 кНм; W red I red 974566071,8 9168934 ,7 см 3 ; y 106,29 r Wred 9168934,7 59,78 мм, Ared 153369,35 здесь γ = 1,25 – коэффициент, учитывающий неупругие деформации бетона (табл. П11 приложения). Так как M = 86,63 > Mcrc = 74,0 кНм – трещины в растянутой зоне образуются. Следовательно, необходим расчет по раскрытию трещин. Определение ширины раскрытия трещин, нормальных к продольной оси Определим приращение напряжения напрягаемой арматуры от действия постоянных и длительных нагрузок σs = σsl, т. е. принимая М = Ml = 67,37 кНм. Поскольку напрягаемая арматура в верхней зоне плиты отсутствует, esp = 0,0, Ms = Мl = 67,37 кН·м и тогда M s 67,37 es 163 0,163 м 163 мм. 0,86. P 413,31 h0 190 M s 67,37 e 163 сечения ,163 мh0=163 es высота 0,86. Рабочая 190мм. мм, s ' 0равна ' a s1 Asp ( ) b b h P 413,31 1475 465,641h0 0190 20,7 90 f f f ,47. a s1 Сечение плиты представляем в виде сечения, заbh0 465,6двутаврового 190 bh0 465,6 1 ' ' менив пустоты(bпрямоугольниками, по площади и ,7 905 a s1 Asp 1475 465эквивалентными ,6 41 20 f b)h f 0 , 47 . a 0,2 s1 f моменту инерции. и465 высота bhШирина ,6 190такого прямоугольника bh0 соот465,6 190 0 es ветственно равны: А = 0,907D = 0,907 · 159 = 144,2 мм; В = 0,866D = 0,866 · 159 = 138 мм. Тогда из рис. 3.4 имеем bf = b′f = 1475 мм; b = (1475 – 7 · 144,2) = 465,6 мм; M s 67,37 es 163 –0138)/2 ,163 м = 163 мм. es h = 0,86. h′ = (220 41 мм. f f413,31 P h0 190 Принимая A′sp = A′s = 0,0, имеем f (b'f b)h'f bh0 1475 465,641 0,47. 465,6 190 – 49 – a s1 a s1 Asp bh0 20,7 905 465,6 190 es приведения 67,37 163 Коэффициент равен 0,163 м 163 мм. 0,86. 13,31 h0 a190 = 300/R = 300/14,5 = 20,7, b)h'f s1 b,ser тогда 1475 465,641 0,47. 465,6 190 a s1 a s1 Asp bh0 20,7 905 0,212. 465,6 190 Рис. 3.4. Эквивалентное сечение пустотной панели При es /h0 = 0,86, φf = 0,47 и μas1 = 0,212 из табл. П12 приложения находим ζ = 0,78, тогда плечо внутренней пары сил z = ζ · h0 = 0,78 · 190 = 148,2 мм. M s / z P 67,37 10 6 / 148,2 413310 45,64 МПа. Asp M s / z905 P 67,37 10 6 / 148,2 413310 sl 45,64 МПа. 905 Asp Аналогично определим значение σs,crc при действии момента escrc = 74,0 M / z P 74,0 10 6 / 152 413310 74кН·м ,0 MS = М 0,94. crc s 81,25 МП h0 413,31 0,19 es Asp M s /905 z P 74,0 10 6 / 152 74,0 0,94. crc h0 413,31 0,19 Asp 905 σssll 860,47 ,63 и μas1 = 0,212 из табл. П12 приложения При es /h0 =M0,94, φ= es / h0 s f 1,1 . находим ζ = 0,8, внутренней пары Ph0тогда 413плечо ,31 0,19 Ms 86 ,63 сил es / h0 Ph0 413 ,31мм. 0,19 z = ζ · h0 = 0,8·190 = 152 s 1,1 . M s / z P 86,63 10 6 / 153,9 413310 165,3 МПа. Asp P 86,63 10 6 / 153,9 413310 M s / z905 s – 50 – 165,3 МПа. 905 Asp M s / z P 67,37 10 6 / 148,2 413310 45,64 МПа. 905 Asp M / z P 74,0 10 6 / 152 413310 74,0 0,94. crc s 81,25 МПа . 413,31 0,19 Asp 905 h0 M / zопределим P 67,37 значение 10 6 / 148,2 σ s413310 Аналогично при действии момента sl s 45,64 МПа. 86S ,6 M =3Мtot = 86,63Asp кН·м. 905 Ms 1,1 . Ph0 413,31 0,19 e /h = Ms 86,63 = = 1,1 . es M⋅s0/,19 z P 74,0 10 6 / 152 413310 74,0 s 0 Ph0 413,31 0 , 94 . 81,25 М crc 6 h 413 , 31 0 , 19 A 905 M s / z P 86,63 10 / 153 , 9 413310 0 sp Поскольку согласно табл. приложения в данном случае при 165П12 ,3 МПа. Asp значении e905 /h = 1,1 φ = 0,47 и μa = 0,212 находим ζ = 0,81, тогда s 0 f s1 M пары сил 86,6z3= ζ · h0 = 0,81 · 190 = 153,9 мм. плечо внутренней e / h0 s 1,1 . Приsмоменте всех Phот 413 ,нагрузок 31 0,19 М = Mtat = 86,63 кН·м значение σs 0 равно s M s / z P 86,63 10 6 / 153,9 413310 165,3 МПа. 905 Asp Проверим условие A > t, принимая t = 0,59, A sl 0,8 s,crc 45,64 0,8 81,25 0,193 t 0,59. s 0,8 s,crc 165,3 0,8 81,25 . Поскольку А < 0, находим непродолжительное раскрытие тре 0,8 81,25 щин по условию (2.3): 0,8. 81,25 sl 1 s, s 1 0A,8 s,crc 0crc ,8 45,640,607 0,193 t 0,59. 165 , 3 + a165 ss a0crc,8= s,acrc ,– 3 acrc3 0,8. 81,25 crc1 crc2 0коэффициент ,8 s,crc 45,64ψs,0принимая ,8 81,25 σs = 165,3 МПа, Вычисляем A sl 0,193 t 0,59. Sred 165 16323024 0 , 8 , 3 0 , 81,25 y0 s s,crc 8 81,25 38,86 мм, s,crc 1/ Rbt,0ser ,8 153369 1 ,35 0,8 413310 0/,1607 Areds P ,55. 165,3 s crc 81,25 трещинами ls. Устанавливаем s 1 0,8 s,расстояния 1 0,8 между 0,607. S red бетона, 16323024 165,3 определенная Высота зоны как для упругоy0растянутого s 38,86 мм, 3 153369,35 413310 / 1,55 A P / R го материала, при S red = 16323024 мм равна bt,ser red S red 16323024 мм, y0 38,86 мм, Ared P / Rbt,ser 153369,35 413310 / 1,55 а с учетом неупругих деформаций растянутого бетона yt = k · y0 = 0,95 · 36,95 = 36,76 мм. Поскольку yt < 2а = 2 · 30 = 60 мм, принимаем yt = 60 мм. Тогда площадь сечения растянутого бетона равна Abt = byt + (bf – b)hf = 465,6 · 60 + (1475 – 465,6)41 = 69321,4 мм2, – 51 – и расстояние между трещинами составляет l s 0,5 Abt 69321,4 d s 0,5 12 459,6 мм. Asp 905 AA ls > 400 мм 69321 Поскольку и ,l4< 40d = 40 · 12 = 480 мм, принимаем l sl 0,05,5Abt 1212459 ,6,6мм. btd s 0,5 69321s,4 d 0 , 5 459 мм. 69321 ,4s 12 45,64 s s bt A 905 ls = 400 мм. sp ls 0,5 A d 0 , 5 459 aspcrcs,1 1 2 905 l s 1,4 ,06,5мм. 0,607 400 0,039 мм. s A 905 E s acrc,1, принимая φ200000 sp (2.6) определяем По формуле = 1,4, φ2 = 0,5, 1 s 4545 ,64 ,64 400 0,039 мм. acrc 1,14, 0 ,05,5 0 ,0607 ,1 1 2 s sl sl 165,30,039 мм. acrc 4 , 607 45 ,64 400 s 2 sE ss s 200000 l 1 , 0 0 , 5 0 ,607 400мм. 0,1 мм. acrc,1,1 1a1crc l 1 , 4 0 , 5 0 , 607 400 0,039 E 200000 , 2 1 2 s s 2 s ss Es Es 200000 200000 По формуле (2.6) определяем acrc,2, принимая φ1 = 1,0, φ2 = 0,5, s 165 ,3,3 165 acrc 1,10,0 0 ,05,5 0 ,0607 40045,64 0,01,1мм. , 2 1 2 s sl sl acrc , 607 мм. 165 ,,3607400 s 2 sE 200000 l 1 , 0 0 , 5 0 ss 1l 2s acrc, 2, 2 1a1crc 1 , 0 0 , 5 0 , 607 400 0,1 400 мм. 0,028 мм. , 3 s s E 200000 2 s ss E 200000 Es 200000 s По формуле (2.6) определяем acrc,3, принимая φ1 = 1,0, φ2 = 0,5, s 4545 ,64 ,64 400 0,028 мм. acrc 1,10,0 0 ,05,5 0 ,0607 ,3 1 2 s sl sl acrc , 607 45 ,64 400 0,028 мм. ,3 1 2 sE ss s 200000 acrc,3 1 2 s E sl s 1,0 0,5 0,607 200000400 0,028 мм. Es 200000 Непродолжительное раскрытие трещин acrc = acrc,1 + acrc,2 – acrc,3 = 0,039 + 0,01 – 0,028 = 0,021 мм, что меньше предельно допустимого значения 0,3 мм. Трещиностойкость пустотной плиты обеспечена. Расчет прогиба плиты 1 Определяем кривизну в середине пролета от продолжиr тельного действия постоянных и длительных нагрузок, т. е. при М = Ml = 67,37 кН·м. R e 18,5 Для этих нагрузок имеем: s 0,86 , φEf = 0,47, yb,sser = 0,607. 6607 МПа. b , red h0 еb1, red 28 10 4 При продолжительном действии нагрузки и нормальной влажR es 18,5 Rb, ser 18,5200000 ности: 28 × МПа. 10-4 при Asp 0,86 Eb, red esb,ser0,86 E 4 6607 E sМПа. εb1,red =6607 b ,a red 4 49,87; a s 2 as2 h0 еhb1, red 28 10 s2 е 28 10 0 b1, red bh0 0,607 6607 s Eb,red влажности окружающей среды 70 ≥ W ≥ 40 %. Тогда Asp Es 200000 E 905 Asp 6 200000 ,37 as2 a s 491, 87; 1 a s 2 Ma49s 2,87 ; a 67 49 ,8710 0,51905 . ,6s 2190 a s 2 3 6 bh0 3 s 2 6607 465 s Eb,red 0,607 bh 465 ,6 190 s Eb,red r 0,607 6607 r 3 bh E 0,48 4650,6 190 6607 c 0 b,red 1 1 67,M 37 106 M 1 1 ,3710 1066 1 / мм. 67 6,65 6,65 10 6 1 / мм 3 3 r r 3 c bh0 Eb,r red r 0,48 465 352 3 , 6 190 6607 – – 0,48 465,6 190 6607 bh E 3 c 0 b,red Rb, ser 18,5 6607 МПа. еb1, red 28 10 4 R es 18,5 0,86 Eb, red b, ser 6607 МПа. h0 еb1, red 28 10 4 A 200000 905 sp s 49,87; a s 2 as2 49,87 0,51. bh0 465,6 190 0,607 6607 b,red Asp E s П13 приложения 200000 при φ = 0,47, e /h 905= 0,51 табл. и μα a sПо 49,87f ; a s 2 s 0 =a0,86 49,87 0,51. s2 2 s2 bh0 465,16 190 s Eb,red 6 0,607 6607 10 Тогда, согласно формуле M находим67 φc,37 = 0,48. 6,65 10 6 1 / мм. (2.15), кривизна r равна 3 3 c bh0 Eb,red 0,48 465,6 190 6607 1 1 67,37 106 M 6,65 10 6 1 / мм. r r 3 c bh03 Eb,red 0,48 465,6 1903 6607 Eb, red По формуле (2.14) определим кривизну, обусловленную остаточным выгибом, при σsb = 86,5 МПа. sb 86,5 1 2,28 10 6 1 мм, 5 r 4 E s h0 2 10 190 где σsb – численно равно сумме потерь напряжений от усадки и пол1 sp6 = 40 + 46,5 = 86,5 1 sp5 86+,5Dσ зучестибетона - 6 МПа. = Dσ 1 1Dσ 6 510 2,28)10 4,37 10- 6 1 мм . ,5 2(6,6 1r sbsb sb r 5 86 , 28 1 мм, 6 r 2 , 28 10 1 мм, Полная кривизна в середине пролета от постоянных и длитель max 3 4 r 4 r E s h0E h 2 10 190 равна 2 10 5 190 s 0 4 ных нагрузок 5 6 2 6 1 2 1 1 f 11 1 Sl - 6 мм. ,37 5 10 -5840 15 2,28)10 4,37 10,53 1 мм . r 14(6,6 2,28)10- 6 4,37 10- 6 1 мм . r 3 max r 4 (6,65 48 r max r max r 3 r 4 Прогиб плиты находим, принимая S = 5/48: 5 1 5 2 15,53 мм. f 1 Sl 2 42,37 10 6 6 5840 f r Sl 4,37 1048 5840 2 15,53 мм. 48 maxr max Согласно СП 20.13330.2011 «Нагрузки и воздействия» поз. 2 при l = 5,84 м предельно допустимый из эстетических требований прогиб равен fult = 5840/200 = 29,2 мм, что превышает вычисленное значение прогиба. Жесткость плиты достаточная. 3.6. Конструкция типовой пустотной панели перекрытия На рис. 3.5–3.7 приведена конструкция типовой пустотной панели серии 1.041.1 «Сборные железобетонные многопустотные плиты перекрытий многоэтажных общественных зданий». – 53 – Рис. 3.5. Конструкция пустотной панели: 1 – каркасы с поперечной арматурой в ребрах панели; 2 – сетки косвенного армирования, усиления зон передачи усилия предварительного напряжения; 4 – конструктивная сетка армирования верхней полки; 5 – продольная предварительно напряженная рабочая арматура; 6 – строповочная петля Рис. 3.6. Узел 1 – расположение строповочной петли; узел 2 – крепление сеток к каркасу с поперечной арматурой (обозначение см. рис. 3.5) – 54 – Рис. 3.7. Узел 3 – армирование крайнего ребра (обозначение см. рис. 3.5) – 55 – 4. ПРОЕКТИРОВАНИЕ РИГЕЛЯ 4.1. Расчетная схема и нагрузки Поперечная многоэтажная рама имеет регулярную расчетную схему с равными пролетами ригелей и равными длинами стоек (высотами этажей), а также с одинаковой нагрузкой по ярусам. Сечения ригелей и стоек по этажам приняты постоянными. Нулевая точка моментов в колоннах расположена в середине высоты этажа. Это позволяет расчленить многоэтажную раму по нулевым моментным точкам на ряд одноэтажных рам с шарнирами по концам стоек. В курсовом проекте рассчитываем ригель среднего яруса. Расчет выполняем с помощью таблиц (табл. П17 приложения), по которым определяются опорные моменты в ригелях по формуле M = (α ∙ qg + β ∙ qv) ∙ l 2, где α и β – расчетные коэффициенты для постоянной и временной нагрузок, зависящие от коэффициента k, равного отношению погонных жесткостей ригеля и стойки, B p ⋅ lk k= , l p ⋅ Bк здесь Вр и Вк – жесткости поперечных сечений ригеля и колонны соответственно; lк и lp – длины колонны и ригеля соответственно. Нагрузка на ригель от ребристых плит при опирании на ригель не менее чем в четырех точках считается равномерно распределенной. Для получения максимальных моментов в расчетных сечениях ригеля его загружают раздельно постоянной и временной нагрузками по схеме, представленной в табл. П17 приложения. Ширина грузовой полосы для расчета погонной нагрузки на ригель равна шагу поперечных рам 6,0 м. – 56 – Расчетная погонная нагрузка на ригель − постоянная нагрузка от собственного веса ригеля с учетом коэффициента надежности по нагрузке γf = 1,1 и перекрытия и коэффициента по ответственности здания γn = 1,0. Предварительно задаемся размерами сечения ригеля b ∙ h = 300 ∙ 800 мм. Нагрузки от перекрытия принимаем из раздела 2 qg = (g ∙ l2 + r ∙ bp ∙ hр ∙ γf) ∙ γп = = (5,675 ∙ 6,0 + 25 ∙ 0,3 ∙ 0,8 ∙ 1,1) ∙ 1,0 = 40,65 кН/м. − временная нагрузка с учетом коэффициента по ответственности здания γп = 1,0 qv = ϑ ∙ l2 ∙ γn = 18,0 ∙ 6,0 ∙ 1,0 = 108 кН/м2; − полная нагрузка q = qg + qv = 40,65 + 108 = 148,65 кН/м. 4.2. Вычисление изгибающих моментов в расчетных сечениях ригеля Жесткости колонны и ригеля при размерах сечения колонны 400×400 мм: 0,4 0,4 3 b h3 4 Bк I к E b 3 Eb b h 3 3 0E,4b 0,04,3002133E b4 м ; b h I12E 0,4 0,412 B E E 0 , 002133 E b м 4; к b b bE b 0,002133bE b м ; Bк I к E b к E 12 12 12 12 b h3 0,3 0,83 3 B p I р Eb 3 Eb b h 3 3 E Eb м 4 . 0,b3 00,8,0128 b h 12 0,3 0,812 B I E E E 40. ,0128Eb м 4 . b b 0,0128 Ebb м B p I р Eb p Eрb b E 12 12 При одинаковом12 классе бетона 12 по прочности на сжатие коэффициент k равен I l 0,0128 4,8 4,82 kI l p k I p lk 0,0128 4,8. ,0128 p Ik l k0 6,0 0,4002133 ,8 4,82. 4,82. к р k l р 6,0 0,002133 I к l р 6,0 0I к,002133 Опорные моменты вычисляют по табл. П17 приложения. Табличные коэффициенты α и β зависят от схем загружения ригеля и коэффициента k – отношения погонных жесткостей ригеля и колонны. Расчетные пролеты ригеля равны расстоянию от оси колонны до оси колонны. Расчетный пролет крайнего ригеля при нулевой привязке крайних колонн l0 = l1 – h/2 = 6,0 – 0,4/2 = 5,8 м. – 57 – – 58 – -0,115·108·5,82= -417,81 -0,032·108·5,82= -116,26 -197,72 -11,87 -161,39 4 5 6 7 -364,26 -266,17 -553,19 -0,036·108·5,82= -130,79 0,009·108·5,82= 33,26 3 Загружение 1+2 Загружение 1+3 Загружение 1+4 -0,063·108·5,82= -228,88 -0,042·108·5,82= -152,59 2 -240,58 -372,77 -539,96 -0,105·108·62= -408,24 -0,062·108·62= -241,05 -0,028·108·62= -108,86 -0,090·40,65·62= -131,72 Опорные моменты, кН м М21 М23 -0,099·40,65·5,86= -135,38 М12 -0,033·40,65·5,82= -45,13 Схема загружения 1 № п/п Опорные моменты ригеля при различных схемах загружения -240,58 -372,77 -298,9 -0,043·108·62= -167,18 -0,062·108·62= -241,05 -0,028·108·62= -108,86 -0,090·40,65·62= -131,72 М32 Таблица 3 Расчетный пролет среднего ригеля равен 6,0 м. Результаты вычисления изгибающих моментов представлены в табл. 3. Пролетные моменты и поперечные силы в ригелях Для определения поперечных сил и изгибающих моментов в пролете из расчетной рамы вырезаем ригель и загружаем его соответствующей расчетному загружению погонной нагрузкой q или qg и сосредоточенными опорными моментами (рис. 4.1). Рис. 4.1. Расчетная схема ригеля первого пролета Схема загружения 1+2 − усилия в первом пролете (погонная нагрузка q): поперечные силы Q12 = ql/2 + (M12 − M21)/l = = 148,65 ∙ 5,8/2 + (197,72 − 364,26)/5,8 = 402,37 кН; Q21 = ql/2 + (M21 − M12)/l = = 148,65 ∙ 5,8/2 + (364,26 − 197,72)/5,8 = 459,8 кН; изгибающий момент в пролете Мl1 = ql 2/8 − (M12 + M21)/2 = = 148,65 ∙ 5,82/8 − (197,72 + 364,26)/2 = 344,08 кН∙м; − усилия во втором пролете (погонная нагрузка qg): поперечные силы Q23 = Q32 = qg l/2 + (M23 − M32)/l = = 40,65 ∙ 6/2 + (240,58 − 240,58)/6 = 121,95 кН; изгибающий момент в пролете Мl2 = qg l 2/8 − M23 = 40,65 ∙ 62/8 − 240,58 = − 57,66 кН∙м. – 59 – Схема загружения 1+3 − усилия в первом пролете (погонная нагрузка qg): поперечные силы Q12 = qgl/2 + (M12 − M21)/l = = 40,65 ∙ 5,8/2 + (11,87 − 266,17)/5,8 = 74,04 кН; Q21 = qgl/2 + (M21 − M12)/l = = 40,65 ∙ 5,8/2 + (266,17 − 11,87)/5,8 = 161,73 кН; изгибающий момент в пролете Мl1 = qg l 2/8 − (M12 + M21)/2 = = 40,65 ∙ 5,82/8 − (11,87 + 266,17)/2 = 31,91 кН∙м; − усилия во втором пролете (погонная нагрузка q): поперечные силы Q23 = Q32 = ql/2 + (M23 − M32)/l = = 148,65 ∙ 6/2 + (372,77 − 372,77)/6 = 445,95 кН; изгибающий момент в пролете Мl2 = ql 2/8 − M23 = 148,65 ∙ 62/8 − 372,77 = 296,16 кН∙м. Схема загружения 1+4 − усилия в первом пролете (погонная нагрузка q): поперечные силы Q12 = ql/2 + (M12 − M21)/l = = 148,65 ∙ 5,8/2 + (161,39 − 553,19)/5,8 = 363,53 кН; Q21 = ql/2 + (M21 − M12)/l = = 148,65 ∙ 5,8/2 + (553,19 − 161,39)/5,8 = 498,63 кН; изгибающий момент в пролете Мl1 = ql 2/8 − (M12 + M21)/2 = = 148,65 ∙ 5,82/8 − (161,39 + 553,19)/2 = 267,78 кН∙м; − усилия во втором пролете (погонная нагрузка q): поперечные силы Q23 = ql/2 + (M23 − M32)/l = = 148,65 ∙ 6/2 + (539,96 − 298,9)/6 = 486,13 кН; Q32 = ql/2 + (M32 − M23)/l = = 148,65 ∙ 6/2 + (298,9 − 539,96)/6 = 405,32 кН; – 60 – изгибающий момент в пролете Мl2 = ql 2/8 − (M23 + M32)/2 = = 148,65 ∙ 62/8 − (298,9 + 539,96)/2 = 249,49 кН∙м. Перераспределение моментов под влиянием образования пластических шарниров в ригеле Практический расчет заключается в уменьшении примерно на 30 % опорных моментов ригеля М21 и М23 по схеме загружения 1+4 как самого большого по абсолютной величине и находящегося в зоне стыка. При этом пластический шарнир образуется на опоре 2. Рис. 4.2. Эпюры изгибающих моментов: а – при упругой работе бетона от загружений 1+2, 1+3, 1+4; б – дополнительная выравнивающая эпюра моментов к загружению 1+4; в – эпюры моментов после перераспределения усилий (показаны эпюры только первого и второго пролетов) – 61 – К эпюре изгибающих моментов загружения 1+4 добавляют выравнивающую эпюру моментов таким образом, чтобы после перераспределения уравнялись опорные моменты М21 = М23 и были обеспечены удобства армирования опорного узла (рис. 4.2). Максимальные положительные значения ординат выравнивающей эпюры моментов на опоре 2: слева DM21 = 0,3 ∙ 553,19 = 165,96 кН·м; справа DM23 = DM21 – (M21 – M23) = = 165,96 – (553,19 – 539,96) = 152,73 кН·м. При этом максимальное значение момента на опоре 2 выровненной эпюры моментов загружения 1+4 по абсолютной величине не должно быть меньше аналогичного значения момента от загружения 1+2. На опоре 1 и 3 к эпюре 1+4 добавляем отрицательные значения моментов до уровня загружений 1+2 на опоре 1 и 1+3 на опоре 3: М 12 ( М112122 М112144 ) (197,72 161,39) 36,33 М 12 ( М 12 М 12 ) (197,72 161,39) 36,33 кН·м; 13 1 4 ) (372,77 298,9) 73,87 кН·м. М 32 ( М132 М132 3 М 32 ( М 32 М 32 4 ) (372,77 298,9) 73,87 Опорные моменты на эпюре выровненных моментов загружения 1+4 будут равны: М12 = –161,39 – 36,33 = –197,72 кН·м; М21 = –553,19 + 165,96 = –387,23 кН·м; М23 = –539,96 + 152,73 = –387,23 кН·м; М32 = –298,9 – 73,87 = –372,77 кН·м. В пролетах после перераспределения значения изгибающих моментов загружения 1+4 увеличились, но они не превысили значений соответствующих моментов от загружений 1+2 и 1+3. Пролетные моменты на эпюре выровненных моментов 1+4 составили Ml1 =267,78 + 64,82 = 332,6 кН·м; Ml2 = 249,49 + 39,43 = 288,92 кН·м. Таким образом, расчетными моментами в пролетах остаются: в первом пролете – Ml1 = 344,08 кН·м загружения 1+2; во втором пролете –Ml2 = 296,16 кН·м загружения 1+3 (рис. 4.2). – 62 – Опорные моменты ригеля на грани колонны являются расчетными моментами для определения площади стыковой арматуры ригеля с колонной. Опорный момент ригеля на грани крайней колонны M(12),1: − по схеме загружения 1+2 M(12),1 = –(M12 – Q12hcol /2) = –(197,72 – 402,37 · 0,4/2) = –123,2 кН·м; − по схеме загружения 1+3 M(12),1 = –(M12 – Q12hcol /2) = –(11,87 – 74,07 · 0,4/2) = 2,94 кН·м; − по схеме загружения 1+4 и выровненной эпюре моментов Q(12) = ql/2 + (M12 – M21)/l = = 148,65 · 5,8/2 + (197,72 – 387,23)/5,8 = 398,4 кН; M(12),1 = –(M12 – Q12hcol /2) = –(197,72 – 398,4 · 0,4/2) = –118,04 кН·м. Опорный момент ригеля на грани средней колонны слева M(21),1: − по схеме загружения 1+2 M(21),1 = –(M21 – Q21hcol /2) = –(364,26 – 459,8 · 0,4/2) = –272,3 кН·м; − по схеме загружения 1+3 M(21),1 = –(M21 – Q21hcol /2) = –(266,17 – 161,73 · 0,4/2) = –233,82 кН·м; − по схеме загружения 1+4 и выровненной эпюре моментов Q(21) = ql/2 + (M21 – M12)/l = = 148,65 · 5,8/2 + (387,23 – 197,72)/5,8 = 463,76 кН; M(21),1 = –(M21 – Q21hcol /2) = –(387,23 – 463,76 · 0,4/2) = –294,48 кН·м. Опорный момент ригеля на грани средней колонны справа M(23),1: − по схеме загружения 1+2 M(23),1 = –(M23 – Q23hcol /2) = –(240,58 – 121,95 · 0,4/2) = –216,19 кН·м; − по схеме загружения 1+3 M(23),1 = –(M23 – Q23hcol /2) = –(372,77 – 445,95 · 0,4/2) = –283,58 кН·м; − по схеме загружения 1+4 и выровненной эпюре моментов Q(23) = ql/2 + (M23 – M32)/l = = 148,65 · 6/2 + (387,23 – 372,77)/6 = 448,36 кН; M(23),1 = –(M23 – Q23hcol /2) = –(387,23 – 448,36 · 0,4/2) = –297,56 кН·м. – 63 – 4.3. Расчет прочности ригеля по сечениям, нормальным к продольной оси Характеристики прочности бетона и арматуры Бетон тяжелый класса В20. Расчетное сопротивление при сжатии Rb = 11,5 МПа; при растяжении Rbt = 0,9 МПа; начальный модуль упругости бетона Eb = 27500 МПа; арматура продольная рабочая класса А400, расчетное сопротивление Rs = 355 МПа; модуль упругости Es = 200000 МПа. Проверка высоты сечения ригеля Проверку выполняют по максимальному моменту (абсолютному значению) по грани опоры согласно схеме загружения 1+4 и выровненной эпюре моментов М(23),1 = 297,56 кН·м при ξ = 0,35, поскольку момент определен с учетом образования пластического шарнира. Вычисляют рабочую высоту сечения: h0 M 297,56 10 6 546 мм, m Rb b 0,289 11,5 300 где αm = ξ(1 – 0,5ξ) = 0,35(1 – 0,5 ∙ 0,35) = 0,2888. Полная высота ригеля h= h0,08 + a10=6 546 + 64 = 610 мм, так как M 344 m 0,255; 2 расстояние от низаRригеля до,5низа арматуры в типовом 11 300 стыковой 625 2 b bh0 ригеле составляет 720 мм и расстояние от верхней грани ригеля до центра этой арматуры 64 мм. Окончательно принимаем вы 1 1 2а′= m 1 1 2 0,255 0,3. соту ригеля кратной 100 Mмм h = 700 297мм. ,56 Принятое 10 6 6 6 сечение провеh0 M 297 56 10 546 мм, M 297 , 56 ,10 ряем по максимальному =344,08 кН·м и 546 h0 h00 ,80 мм,мм, ,289 моменту 11,5 300 Ml1 546 ,8m Rпролетному bb 0 R b 0 , 289 11 , 5 300 531 R b 0 , 289 11 , 5 300 m b R m b h0 = h – a = 700 – 75 =R625 мм, 355 где а = 75 мм при вертикальном рас1 1 s большого положении двух стержней диаметра. 700 700 M 344,08 10 6 6 6 m 344,344 08 210 0,255; M M 08 ,10 02 11 0,255; m Rmb bh 2 ,5 300 625 2 20,255; 2 ,5 300 Rb bhR0b bh011,511 300 625 625 1 1 2 m 1 1 2 0,255 0,3. 0,255 1 11 21m2 m1 11 210,2255 0,3. 0,3. Граничная высота сжатой зоны бетона (табл. П9 приложения): 0,8 0,8 R 0,8 0,8 0,8 0,80,531, 0,,531, R R Rs 355 0,531 1 Rs R1s 355 355 1 1 1 700 1 700 700 700 700 700 – 64 – условие ξ ≤ ξR выполняется, следовательно, принятая высота сечения достаточна. Нагрузку от собственного веса ригеля не пересчитываем, так как уменьшение общей нагрузки на ригель составило 1,1 %. Площадь продольной нижней арматуры в пролете крайнего ригеля: R bh 11,5 300 625 0,3 1822 мм 2 . As b 0 355 Rs Принято 2 диаметра 28 с As = 1232 мм2 и 2 диаметра 20 с As = 628 мм2 с общей площадью As = 1860 мм2. 123 ,2 10 6 0,087; 1 1 2 0,87 0,0912. Сечение наm крайней опоре 11,5 300 636 2 М R bh = 123,2 =h0,– – 64 = 636 мм, 11кН·м, h625 ,5bh 300 3 a = 700 0 ,3 2 . 1822 0мм As (12),1b 0A11,5R b300 0 11,5 300 625 1822 мм 2на . фикси 636 0 , 0912 s 355ригеля 355 так как выпуски из должны находиться ARss арматуры 564 , 2 R s 625 0,3 R bh 11 , 5 300 0 рованной арматуры из колонны. выпусков355 1822 мм 2 . As b высоте 355 Rs 6 123,2 10 6 6 ,10 ,56 10 m M 123 ,20297 087 ; 0,087 1 ; 01,213 2;10,871 2 102,0912 0. ,243. 10 ,872. 0,0213 ,0912 m 636 2 2 2 11,5m 300 6Rb bh 11 , 5 300 636 11 , 5 300 636 0 123,2 10 mПлощадь 0,087; 1 1 2 0,87 0,0912. арматуры 11,511 300 636 2636 0,0912 ,5 300 11,5 300 636 0,0912 As ,2 564,2 мм2. 564 A s 355 355 11,5 300 636 0,0912 A sПринято 2 мм2. 2 диаметра 20 сA564 = ,628 s 6 6 M355 297 , 56 10 297,560,М 10(23),1 Сечение опоре слева и справа ;1кН·м. 210,213 . 0,243. m на 2M 213 ; =297,56 2 1 20,243 0,213 0,1213 2 636 2 Rb bh02m 11R,5bh 300 6 11,5 300 636 0 b 10 M 297,56 m 0,213; 1 1 2 0,213 0,243. 2 2 Rb bh0 11,5 300 636 Площадь арматуры 11,5 300 636 0,243 1500 мм2. 355 11,528 300 0,243 Принято 3 диаметра с As 636 = 1847 мм2. 1500 A s 0,243 11 , 5 300 636 M 1500 355296,16 10 6 в среднем пролете AСечение s 0,21; 1 1 2 0,21 0,238. m 2 355 Rb bh02 h = 11h,5– 300 700 640– Мl2 = 296,16 кН·м, a = 60 = 640 мм. M 0 296,16 10 6 m296 ,16 102 6 0,21; 1 1 2 0,21 0,238. M 2 Rb bh0 11,50,21 300 640 1 1 2 0,21 0,238. m ; Rb bh02 11,5 11 300 640 2 640 0,238 ,5 300 1479 As Площадь арматуры 355 11,5 300 640 0,238 1479 мм2. s 0,238 11,5 300 A 640 57,66 10 6 355 As 1479 m 0,041; 1 1 2 0,041 0,042. 355 2 11,5 300– 636 65 – 57,66 10 6 6 m 57,66 10 11,5 300 636 2 0,041; 1 1 2 0,041 0,042. m 0,041; 1 1 2 0,041 0,042. As 2 m m Rb bh02 Rb bh02 11,52 300 0,21 ; 2 1 1 2 0,21 0,238. 640 11,5 300 640 11,5 300 0,238 Принято с A s640 = 1520 мм2.1479 A s 640 22 11,45 диаметра 300 0,238 1479 A 355 s Сечение в среднем 355 пролете на действие отрицательного момента М = –57,66 кН·м. 57,66 10 6 0,041; 1 1 2 0,041 0,042. 57,66 10 6 m m 0,041 11,52 300 636; 2 1 1 2 0,041 0,042. 11,5 300 636 Площадь арматуры 11,5 300 636 0,042 Ass 636 0,042 A 261 мм2. 11,5 300 As 355 261 355 Принято 2 диаметра 14 с As = 308 мм2. 4.4. Расчет прочности ригеля по сечениям, наклонным к продольной оси Проверка прочности по сжатой полосе между наклонными трещинами Прочность бетонной полосы проверяем по максимальной перерезывающей силе Q21max = 463,76 кН по схеме загружения 1 + 4 и выровненной эпюре моментов. Максимальная поперечная сила на грани опоры: Q = Qmax – q · hcol /2 = 463,76 – 148,65 · 0,4/2 = 434,03 кН; Qmax = 434,03 < 0,3Rbbh0 = 0,3 · 11,5 · 300 · 546 = 558900 H = 558,9 кН, т. е. прочность полосы обеспечена. Минимальный диаметр поперечных стержней из условия свариваемости контактной сваркой с продольными стержнями диаметром 28 мм – 8 мм. Принимаем диаметр поперечных стержней 12 мм А400 с Rsw = 285 МПа. Рабочая высота сечения h0 = 636 мм.Максимальный шаг поперечных стержней по конструктивным требованиям: sw = h0 /2 = 636/2 = 318 мм и не более 300 мм. Принимаем шаг sw = 180 мм As = 113 мм2. В каждом ригеле устанавливают пространственный каркас, состоящий из двух плоских, при этом Asw = 2 · 113 = 226 мм2. Проверка прочности наклонных сечений. Крайний ригель Поперечные силы Q12 = 380,76 кН по схеме загружения 1+2, Q21 = 463,76 кН по схеме загружения 1+4 и выровненной эпюре мо- – 66 – ментов. Каркасы выполняют симметричными, и расчет ведут по максимальной перерезывающей силе на грани опоры Q = 463,76 кН. Определяют интенсивность хомутов: R A 285 ⋅ 226 qsw = sw sw = = 357,7 Н/мм, sw 180 проверяют условие qsw > 0,25Rbt b = 0,25 · 0,9 · 300 = 67,5 Н/мм. Условие выполняется, следовательно, полностью учитываются Mb ⋅ 106 163,82хомуты c= = = 1316 мм < 3h0 = 3 ⋅ 636 = 1908 мм, в расчете. Вычисляют qMb: 94,65 1 Mb = 1,5Rbt bh02 = 1,5 · 0,9 · 300 · 6362 = 163,82 · 106 Н · мм. НаходятRдлину невыгоднейшего наклонного сечения с. A проекции 285 M ⋅ 226 163,82 ⋅ 10 6 qsw = sw swQb== b = = 357,7 = 124483 Н = 124,483 кН; Поскольку 0,9 · 300 = 1,33 < 2, значение с опреs q R/RA b180 285 ⋅ 1316 226 c= 357,7/ qsw w=sw sw btsw = = 357,7 деляем по формуле sw 180 2 R bh 6 0,9 ⋅ 300 ⋅ 636 2 285 ⋅ 226 163 M b s max =,82bt⋅ 100 == 1316 мм < 3h ==3235 ,5 = 1908 q sw2мм, = = 161,03 c= = ⋅ 636 Q 6 463760 0 400 q1 M b 94,65 163,82 ⋅ 10 c= = = 1316 мм < 3h0 = 3 ⋅ 636 = 1908 мм, ,65· 108 = 94,65 кН/м. где q1 = q – 0,5qv =q1148,65 –94 0,5 R A = 2h 285=⋅ 22626 Принимаем · 636 = 1272 q =M sw сsw ,7 мм < с. Тогда = 357 163,82 0 = 0 ⋅ 10 Qbsw= b s=w Н = 124,483 кН; 180 = 124483 6 c M b 1316 163,82 ⋅ 10 = = 124483 Н = 124,483 кН; Qb = c 13166 2 2 M ⋅357,7 ,82⋅·300 10 ⋅ 636 Rbtb bhc 0 =163 0,9 ⋅ 226 285 Qsswc== 0,75q 0,75 ·1316 1272 = 341246 Н кН; = = <,53h0 = = 1908 3 ⋅2= 636 мм, = = = мм 235 sw 0 q sw =341,246 = 161,03 max 2 ,65 2 q1 Q Rbt bh94 463760 0,9 ⋅ 300 ⋅ 636 400 285 ⋅ 226 0 = – q c ==463,76 – 94,65 · 1,316 = 235,= 5 339,2 q swкН; = 161,03 Q s=max Qmax 2 = 285 ⋅ 226 sw Asw Q1 463760 400 = = 357,7 sw 180 124,48⋅ 10 +6341,25 = 465,73 > Q = 339,2 кН. Qb + MQsw =163,82 Qb = b = = 124483 Н = 124,483 кН; c наклонных 1316 сечений обеспечена. Проверяют требоПрочность 6 Mb 163,82 ⋅ 10 вание = = 1316 мм < 3h02 = 3 ⋅ 636 = 1908 мм, R bh 0,9 ⋅ 300 ⋅ 636 2 94,65 285 ⋅ 226 1 s max = bt 0 = = 235,5 ммq>sws2w == 180 мм, = 161,03 Q 463760 400 принятый шаг хомутов не превышает максимального значения. 6 M b 163,82 ⋅ 10 = =В 124483 Н =части 124,483 кН; принимаем шаг поперечных стержней средней ригеля c 1316 sw2 = 400 мм < 0,75h0. Таким образом, принятая интенсивность хому- Rbt bh02 0,9 ⋅ 300 ⋅ 636 2 285 ⋅ 226 = = 235 ,5 тов в пролете равна q sw2 = = 161,03 н/мм. Q 463760 400 Проверяем условие qsw2 ≥ 0,25Rbtcb = 0,25 · 0,9 · 300 = 67,5 н/мм, условие выполняется. Определяем длину участка l1 с интенсивностью хомутов qsw1. Так как – 67 – Dqsw = 0,75(qsw1 – qsw2) = 0,75(357,7 – 161,03) = = 147,5 Н/мм > q1 = 94,65 Н/мм, значение l1 вычислим, приняв Qb,min = 0,5Rbt bh0 = 0,5 · 0,9 · 300 · 636 = 84375 Н; l1 = = Qmax − (Qb,min + 1,5q sw2 h0 ) q1 − 2h0 = 463760 − (84375 + 1,5 ⋅ 161,03 ⋅ 636) − 2 ⋅ 636 = 1113 мм. 94,65 Принимаем длину участка с шагом хомутов sw1 = 180 мм, равной 1,26 м. В среднем ригеле поперечная сила Q23 = 437,59 кН по схеме загружения 1+4 и выровненной эпюре моментов практически равна расчетной поперечной силе в крайнем пролете. Не пересчитывая, во втором пролете принимают такой же шаг поперечной арматуры. 4.5. Конструирование арматуры крайнего ригеля Армирование опорных зон с применением дополнительных каркасов Стык ригеля с колонной выполняют на ванной сварке выпусков верхних надопорных стержней и сварке закладных деталей ригеля и опорной консоли колонны. Ригель армируют двумя плоскими каркасами, объединенными в пространственный. Диаметр двух верхних конструктивных продольных стержней пространственного каркаса принимают равным 14 мм. Для стыка ригелей с крайней колонной требуются два стержня диаметром 20 мм, для стыка ригелей со средней колонной – три стержня диаметром 28 мм. Q необходимы − (Qb, min + два 1,5qдополнительных Следовательно, в верхней зоне sw 2 h0 ) l1 = max − 2h0 = q1 верхних плоских каркаса. Один с двумя стержнями диаметром 20 мм – слева и один плоский каркас с тремя стержнями 28 мм 463760 − (84375 + 1,5 ⋅ 161,03 ⋅ 625 ) – справа. = − 2 ⋅ 625 = 1163 мм. Вычислим несущую способность сечения с двумя опорными 94,65 2 стержнями 20 мм с As = 628 мм . Высота сжатой зоны бетона в расчетном сечении: x= R A 355 ⋅ 308 Rs As 355 ⋅ 628 = 31,7 = 64,62 мм. x= s s = = Rb b 11,5 ⋅ 300 Rb b 11,5 ⋅ 300 – 68 – Несущая способность сечения: bx(h –10,5x) QM ,5qsw 2=h011,5 ) · 300 · 64,62 · (636 – 0,5 · 64,62) = b , min0 + max=−R(bQ − 2h0 = = 134,59 кН·м. q1 Определим длину каркаса с двумя стержнями диаметром 20 мм. 463760 − (84375 + 1,5 ⋅ 161 ,03 ⋅ 625 ) = − 2 ⋅ 625 = 1163 мм. Для этого установим несущую способность опорного сечения с дву94,65 мя диаметрами 14 мм с As = 308 мм2. Высота сжатой зоны бетона в расчетном сечении: l1 = x= Rs As 355 ⋅ 628 R A 355 ⋅ 308 = 64,62 x = s s = = 31,7 мм. = Rb b 11,5 ⋅ 300 Rb b 11,5 ⋅ 300 Несущая способность сечения: M = Rb bx(h0 – 0,5x) = 11,5 · 300 · 31,7 · (636 – 0,5 · 31,7) = 67,82 кН·м. Место теоретического обрыва двух опорных стержней диаметром 20 мм у крайней колонны и трех опорных стержней диаметром 28 мм у средней колонны от оси крайней колонны определяем аналитическим методом по загружению 1+4 и выровненной эпюре моментов: М12 = 197,72 кН·м; М21 = –387,23 кН·м; Q12 = 398,4 кН; Q21 = –463,76 кН; q = 148,65 кН/м. Изгибающий момент в месте теоретического обрыва стержней Мх = –67,82 кН·м на расстоянии х от левой опоры. Mx = Q1x – qx2/2 – M12 = –67,82 =398,4 · x – 148,65 · x2/2 – 197,22); x2 = 5,36 · x + 1,748 = 0; x1 = 5,01 м; x2 = 0,35 м. Стыковые стержни диаметром 20 мм заводят за точку теоретического обрыва на длину анкеровки W = (Q/2qsw) + 5d. Длина анкеровки двух стыковочных стержней при перерезывающей силе в рассматриваемом сечении: Qx = Q12 – qx = 398,4 – 148,65 · 0,35 = 346,4 кН; 346,4 ⋅ 10 3 346,4 ⋅ 10 3 W2 = + 5 ⋅ 20 = 584 мм. + 5 ⋅ 28 = 624 2 ⋅ 357,7 2 ⋅ 357,7 Расстояние от оси крайней колонны до места обрыва двух стыковых стержней диаметром 20 мм: W1 = R A 355 ⋅ 1860 l R= A 0,35 + 0,584 = 0,93 м. 355 ⋅ 1847 = 190 x = s s = = 191,39 x =1 s s = 11,5 ⋅ 300 стержней уRсредней 11,опоры 5 ⋅ 300 Rb bстыковочных Длина анкеровки трех bb при перерезывающей силе в рассматриваемом сечении: – 69 – Qx = Q12 – qx = 398,4 – 148,65 · 5,01 = –346,4 кН; W1 = x= 346,4 ⋅ 10 3 346,4 ⋅ 10 + 5 ⋅ 20 = 584 W2 = + 5 ⋅ 28 = 624 мм. 2 ⋅ 357,7 2 ⋅ 357,7 Расстояние от оси крайней колонны до места обрыва трех стыковых стержней диаметром 28 мм: 3 3 3 Rs As 355 ⋅ 1847 lRs=A346 – 0,624 = 4,386 м. 355 ⋅ 1860 s5,01 191 39 W2 = 346,4 ⋅ 10 + 5 ⋅ 28 = 624 = 190 x =W12 = = = ,4 ⋅ 10 + 5 ⋅=20 =,584 11,5,7⋅ 300 ⋅ 300 Rb b 11,5Определяем Rb b 2 ⋅способность 357 2 ⋅ 357 несущую опорного сечения с ,7тремя верхними стыковыми стержнями диаметром 28 мм с As = 1847 мм2. Высота сжатой зоны бетона в расчетном сечении: R A 355 ⋅ 1847 R A 355 ⋅ 1860 = 190 мм. = 191,39 x= s s = x= s s = Rb b 11,5 ⋅ 300 Rb b 11,5 ⋅ 300 Несущая способность сечения: M = Rb bx(h0 – 0,5x) = 11,5 · 300 · 190 · (636 – 0,5 · 190) = 354,63 кН·м, что больше момента на грани колонны М = 297,56 кН·м. По результатам конструирования ригеля строим эпюру материалов (рис. 4.3). В нижней зоне обоих ригелей расположено по четыре стержня, два из которых не доводят до опор, а обрывают в пролете в соответствии с эпюрой изгибающих моментов. Устанавливаем фактическую несущую способность сечения крайнего ригеля с нижней рабочей 3 2 диаметра 28346 мм,4и⋅ 10 2 диаметра 20 мм. Фактическую рабо346,4 ⋅ арматурой 10 3 W = W1 = + 5 ⋅ 20 = 584 + 5 ⋅ 28 = 624 2 2 ⋅ 357чую ,7 высоту сечения определяем 2 ⋅ 357,7 из рис. 4.4: h0 = 700 – 62 = 638 мм; As = 1860 мм2. Высота сжатой зоны бетона в расчетном сечении: R A 355 ⋅ 1847 R A 355 ⋅ 1860 = 190 x = s s = = 191,39 мм. x= s s = Rb b 11,5 ⋅ 300 Rb b 11,5 ⋅ 300 Несущая способность сечения: M = Rb bx(h0 – 0,5x) = 11,5 · 300 · 191,39 · (638 – 0,5 · 191,39) = = 358,08 кН·м. Два стержня диаметром 20 мм обрываем в пролете и определяем фактическую несущую способность сечения с нижней рабочей арматурой 2 диаметра 28 мм. Фактическую рабочую высоту сечения определяем из рис. 4.4: h0 = 700 – 44 = 656 мм; As = 1232 мм2. – 70 – Рис. 4.3. Эпюра материалов ригеля первого пролета Рис. 4.4. Схема расположения нижней арматуры – 71 – Высота сжатой зоны бетона в расчетном сечении: R A 355 ⋅ 1232 161,6 ⋅ 103 = 126,77 мм. x= s s = W3 = + 5 ⋅ 20 = 326 Rb b 11,5 ⋅ 300 2 ⋅ 357,7 Несущая способность сечения: M = Rb bx(h0 – 0,5x) = 11,5 · 300 · 126,77 · (656 – 0,5 · 126,77) = ⋅ 10 3 кН·м. 161=,6259,185 W4 = + 5 ⋅ 20 = 326 2 ⋅обрыва 357,7 стержня находим аналитическим Места теоретического методом (рис. 4.3) по загружению 1+2: М12 = –197,72 кН·м; М21 = –364,26 кН·м; Q12 = 402,37 кН; Q21 = –459,8 кН; q = 148,65 кН/м. Изгибающий момент в местах теоретического обрыва стержня Мх = 259,18 кН·м. Mx = Q1x – qx2/2 – M12 = 259,18 =402,37 · x – 148,65 · x2/2 – 197,72; x2 – 5,41 · x + 6,14 = 0; x1 = 3,79 м; x2 = 1,62 м. Место теоретического обрыва стержня находится на расстоянии 1,92 и 3,21 м от оси крайней колонны. Длина анкеровки стержня со стороны крайней колонны при перерезывающей силе в рассматриваемом сечении: Qx2 = Q12 – qx = 402,37 – 148,65 · 1,62 = 161,60 кН; x= Rs As 355 ⋅ 1232 161,6 ⋅ 103 = 126,77 W3 = = + 5 ⋅ 20 = 326 мм. Rb b 11,5 ⋅ 300 ,7 ⋅ 1232 Rs2A⋅s357355 161,6 ⋅ 103 ,77 Wколонны = 126 x =стержня = со стороны + 5 ⋅ 20 = 326 3 = Длина анкеровки средней Rb b 11,5 ⋅ 300 2 ⋅ 357при ,7 перерезывающей силе в рассматриваемом сечении: W4 = Q = Q – qx = 402,37 – 148,65 · 3,79 = –161,6 кН; 161,6 ⋅ 10 3 + 5 ⋅ 20 =x2326 12 2 ⋅ 357,7 161,6 ⋅ 10 3 W4 = + 5 ⋅ 20 = 326 мм. 2 ⋅ 357,7 Сечение фактического обрыва стержней находится на расстоянии l3 = 1,62 – 0,33 = 1,29 м и l4 = 3,79 + 0,33 = 4,12 м от оси крайней колонны. Конструктивная длина ригеля крайнего пролета при нулевой привязке колонн крайнего ряда с учетом зазоров между колонной и ригелем, равных 50 мм, будет составлять – 72 – L = l1 – 1,5hcol – 2a – 20 мм = = 6000 – 1,5 · 400 – 2 · 50 – 20 = 5280 мм, где l1 – расстояние между координационными осями крайнего и внутреннего ряда колонн; hcol – высота сечения колонн; а – номинальная величина зазора между ригелем и колонной, равная 50 мм; 20 мм – дополнительный зазор, обеспечивающий удобство монтажа. Конструктивная длина каркасов принимается на 10–15 мм меньше конструктивной длины ригеля для удобства установки их в форму. Минимальная величина защитного слоя бетона и минимальное расстояние между продольными стержнями принимается в соответствии с указаниями главы 5 [2]. Конструирование ригеля среднего пролета выполняют аналогичным методом. 4.6. Конструкция типового ригеля На рис. 4.5–4.13 приведены примеры конструирования и армирования типового ригеля таврового сечения с полкой внизу серии 1.420-35 «Конструкции многоэтажных производственных зданий с сетками колонн 6×6 и 9×6 м». Ригель прямоугольного сечения конструируется аналогичным образом, за исключением армирования нижней полки, которая отсутствует. Обозначения сечений и каркасов взяты из типовой серии. – 73 – Рис. 4.5. Опалубочные размеры ригеля серии 1.420-35 Рис. 4.6. Опалубочные размеры поперечного сечения ригеля серии 1.420-35 – 74 – Рис. 4.7. Армирование ригеля: 1 – нижняя рабочая арматура ригеля; 2 – пространственный каркас ригеля Рис. 4.8. Опорное и пролетное сечения ригеля: 1 – плоский каркас пространственного каркаса Рис. 4.9. Армирование концевого участка ригеля: 1 – пространственный каркас – 75 – Рис. 4.10. Пространственный каркас ригеля: 1, 2 – плоские каркасы с нижней продольной и поперечной арматурой; 3, 4 – гнутые сетки армирования полки; 5 – опорная закладная деталь с анкерными стержнями; 6 – закладная деталь для плит покрытий; 7 – соединительные стержни пространственного каркаса; 8, 9 – стыковые стержни дополнительного плоского каркаса; 10 – поперечные стержни дополнительного каркаса, с помощью которых он крепится к пространственному каркасу; 11 – поперечные стержни опорной зоны (см. рис. 4.11); 12 – закладная деталь для крепления дополнительных хомутов стыковой зоны; 13 – стыковой плоский каркас – 76 – Рис. 4.11. Плоский каркас ригеля Рис. 4.12. Арматурные сетки полки ригеля Рис. 4.13. Составной стержень ригеля – 77 – 5. ПРОЕКТИРОВАНИЕ РЕБРИСТОГО МОНОЛИТНОГО ПЕРЕКРЫТИЯ С БАЛОЧНЫМИ ПЛИТАМИ 5.1. Компоновка конструктивной схемы ребристого монолитного перекрытия с балочными плитами Ребристое монолитное перекрытие с балочными плитами состоит из плиты, работающей по короткому направлению, второстепенных и главных балок. Все элементы перекрытия монолитно связаны и выполняются из бетона класса В15. Сетка координационных осей l1 × l2 = 6 × 6 м. Главные балки располагают в поперечном направлении здания и опирают на продольные стены толщиной 510 мм с пилястрами сечением 130×510 мм. Привязка внутренней грани стены толщиной 510 мм к продольным и поперечным осям – 120 мм. Высота главных балок составляет (1/8…1/15)l1, второстепенных – (1/12…1/20)l2. Принимаем высоту главных балок l1 /10 = 6000/10 = 600 мм, второстепенных l2 /12 = 6000/12 = 500 мм, ширину балок – 300 и 250 мм соответственно. Второстепенные балки располагаем с шагом l1 /3 = 2 м вдоль здания по продольным координационным осям и между ними еще две балки. Толщину плиты принимаем 80 мм (рис. 5.1). 5.2. Расчет монолитной плиты перекрытия Расчетная схема и усилия в плите Для расчета плиты из состава покрытия поперек второстепенных балок вырезаем полосу шириной 1 м. Расчетная схема плиты – многопролетная неразрезная балка. Расчётный пролёт плиты равен расстоянию в свету между второстепенными балками l0 = 2,0 – 0,25 = 1,75 м, для крайнего пролета от центра площадки опирания на стену до второстепенной балки l0 = 2,0 – 0,25/2 – 0,12/2 = 1,815 м (рис. 5.2). – 78 – – 79 – Рис. 5.1. План монолитного ребристого перекрытия с балочными плитами Нагрузку на плиту подсчитываем в табличной форме (табл. 4). Рис. 5.2. Расчетный пролет плиты Таблица 4 Нормативные и расчетные нагрузки на 1 м2 перекрытия № п/п Коэффици- РасчетНормативные ент надёж- ные нанагрузки, ности по грузки, 2 кН/м нагрузке кН/м2 Вид нагрузки Постоянные 1. Собственный вес плиты 25×0,08×1 = 2,0 2. Конструкция пола керамическая плитка на цементно-песчаном растворе δ = 20 мм 18×0,02×1 = 0,36 армированная цементно-песчаная стяжка δ = 35 мм 20×0,035×1 = 0,70 песчаная засыпка δ = 70 мм 17×0,07×1 = 1,19 Итого постоянная 1,2 2,4 0,36 1,3 0,468 0,70 1,3 0,91 1,19 1,3 1,547 4,25 3. Временная нагрузка 4. Полная 2,0 15 19,25 – 80 – 5,325 1,2 18 23,325 Расчетная погонная нагрузка на расчетную полосу плиты шириной 1 м: q = (g + v) · 1 · gn = 23,325 · 1,0 = 23,325 кН/м. Изгибающие моменты определяют как для многопролетной неразрезной балки с учетом перераспределения моментов: − в средних пролетах и на средних опорах M = ql 2/16 = 23,325 · 1,752/16 = 4,466 кН·м; − в первом пролете и на первой промежуточной опоре M = ql 2/11 = 23,325 · 1,8152/11 = 6,985 кН·м. При отношении h/l ≥ 1/30 в плитах, окаймленных по всему контуру монолитно связанными балками, под влиянием возникающих распоров изгибающие моменты уменьшают на 20 %. Отношение h/l = 80/1750 = 1/22 > 1/30, следовательно, влияние распора учитывается. Величина изгибающих моментов в плитах, окаймленных по всему контуру монолитно связанными балками, составит М1 = 0,8 · 4,466 = 3,573 кН·м. Расчет плиты по первой группе предельных состояний. Характеристики прочности бетона и арматуры Бетон тяжелый класса В15; расчетное сопротивление бетона на сжатие Rb = 8,5 МПа. Арматура сеток – проволока класса В500, Rs = 415 МПа. Подбор сечения продольной арматуры в средних пролетах и на средних опорах плиты между осями «1» и «2» Рабочая высота сечения h0 = h – a = 80 – 15 = 65 мм. M 4,466 ⋅10 6 6 M 4,466 ⋅10 = 0,1244; αm = = α m R= bh 2 2 8=,5 ⋅ 1000 ⋅ 65 2 2 = 0,1244; 6 b R 0bh 8,5 ⋅ 1000 ⋅ 65 M 4,466 ⋅10 b 0 αm = = = 0,1244; 2 2 Rb bh0 8,5 ⋅ 1000 ξ = 1⋅ 65 − 1 − 2α = 1 − 1 − 2 ⋅ 0,1244 = 0,133; ξ = 1 − 1 − 2mα m = 1 − 1 − 2 ⋅ 0,1244 = 0,133; ⋅ 65;⋅ 0,133 8,5 ⋅1000 ξ = 1 − 1 − 2α m А= 1=−Rb1bh −02ξ⋅ =0,1244 = 0,133 = 177,35 мм 2. s 415 Rs 5В500 − 100 5В500 − 100 2960 × Принимают 10Rbдиаметров 5В500 = 196 мм2 и соответстbh0о 8,5 ⋅ 1000 ⋅ 65с⋅ 0A,133 2 s − 200 296 Аs = Rbbh0=о 8,5 ⋅ 1000 ⋅ 65 ⋅ 0,133 = 177,35 мм . 2 4 В4500 Аs = Rs = ,35 мм . 55В500 − 200 5В500= −177 100 415 2960 × L . 415 Rsсетку марки 8,5 ⋅рулонную 1000 ⋅ 65 ⋅ 0,133 Rвующую 2 b bh0о 20 4 В500 − 200 Аs = = = 177,35 мм . 415 Rs – 81 – Так как плита армируется рулонными сетками, то эта сетка является основной на всю ширину здания. В первом пролете и на первой промежуточной опоре раскатывают дополнительную сетку, которая рассчитывается на изгибающий момент М = 6,985 – 4,466 = 2,52 кН·м. Рабочая высота сечения h0 = h – a = 80 – 15 = 65 мм. M 2,52 ⋅ 10 6 6 αm = = M 2,52 ⋅ 10 = 0,07; α mR=b bh02 28,=5 ⋅1000 ⋅ 65 2 2 = 0,07; Rb bh0 8,5 ⋅1000 ⋅ 65 αm = M 2,52 ⋅ 10 6 = 1;− 1 − 2 ⋅ 0,07 = 0,0728; =ξ = ξ1 −= 11−− 212α −=m20α,07 2 m = 1 − 1 − 2 ⋅ 0,07 = 0,0728; Rb bh0 8,5 ⋅1000 ⋅ 65 R bh ξ 8,5 ⋅1000 ⋅ 65 ⋅ 0,0728 = 96,95 мм 2 . 2 Аs = b Rb0bh0=о 8,5 ⋅ 1000 ⋅ 65 ⋅ 0,0728 − 100 А = = = 96,95 мм . 2 4 В500 о 8 , 5 1000 65 0 , 0728 R bh ⋅ ⋅ ⋅ 415 R 2960 × s 4 В500 − 100 b 0 ξ = 1 − 1 − 2α m = А 1 −s=R1 − 2 ⋅ 0,07= = 0,0728 ; = 96,95 мм .3В500 415 29 s 200 − s 2 415 R Принимают 10 диаметров 4В500 с As = 126 мм и соответствую3В500 − 200 s Rbbh0о 8,5R⋅ 1000 ⋅ 65 ⋅80,,50728 2 55 4 В500 − 100 ⋅1000 ⋅ 65 ,105 b bh0 ξрулонную Аs =дополнительную = =сетку 96 ,95⋅ 0 мм . = 139 щую марки = ,8 мм 2. 2960 × L . Rs Аs = R 415 20 3В500 − 200 415 s Между главными балками на всю ширину здания раскатывают две основные сетки и по две дополнительные сетки с каждого края Rb bh0 ξ 8,5 ⋅1000 ⋅ 65 ⋅ 0,1 = = 133,1 мм 2. (рис. 5.3). Аs = Rs 415 Рис. 5.3. Схема армирования плиты рулонными сетками – 82 – Подбор сечения продольной арматуры в средних пролетах и на средних опорах в плитах, окаймленных по контуру балками Рабочая высота сечения h0 = h – a = 80 – 15 = 65 мм. M1 3,573 ⋅ 10 6 6 αm = M2 1= 3,573 ⋅ 102 = 0,0995; αRm R =b bh = 0,0995; 85=,5⋅1000 ⋅ 1000⋅ 65 ⋅ 65 0 2 2 ξ bh 8 , ⋅ 0,0728 = 0 8,5 ⋅ 1000 ⋅ 65 = 96,95 мм 2 . Аs = b 0Rb bh 415 Rs M 1 ξ = 1 −3,573 1 −⋅ 10 2α6 m = 1 − 1 − 2 ⋅ 0,0995 = 0,105; αm = = = 0 , 0995 ξ = 1 − 1 − 2α = 1 − ; 1 − 2 ⋅ 0,0995 = 0,105; Rb bh02 8,5 ⋅ 1000 ⋅ 65 2 m Rb bh0 ξ 8,5 ⋅1000 ⋅ 65 ⋅ 0,105 = 8,5 ⋅ 1000 ⋅ 65 ⋅ 0,105= 139,8 мм 22. 5В500 − 125 Аs = R b bh0о А = = 139,8 мм . 2 5В500 − 125 415 RsRbbh0=о ⋅ 08,0995 ,5 ⋅ 1000 ⋅ 65; ⋅ 0,105 2960 × L ξ = 1 − 1 − 2sαА = 0,105 ms ==1R−s 1 − 2 = = 139,8 мм .4 В500 − 200 2960 × 415 2 415 R Принимают 8 диаметров 5В500 с As = 157,1 мм и соот4 В500 − 200 s ξ ⋅ 658⋅,50,⋅105 1000 Rbbh0о 8R,5b⋅bh 1000 ⋅ 65 ⋅ 0,1 2 5В500 −2125 0 Аs = ,8 мм=. 133,1 мм . 2960 × L 55 . = сетку= 139 А ==рулонную ветствующую марки 415 Rs s 415 Rs 20 4 В500 − 200 Эта сетка является основной на всю ширину здания. В первом пролете и на первой промежуточной опоре раскатывают дополRb bh0 ξ рассчитывается 8,5 ⋅1000 ⋅ 65 ⋅ 0,0728 нительную сетку, на изгибающий = = 96,95 мм 2 . момент Аs = которая 415 Rs кН·м. М = 6,985 – 3,573 = 3,412 M 3,412 ⋅ 10 6 6 αm = = M2 3,412 ⋅ 10 2 = 0,095; Rb bh 8 , 5 ⋅ 1000 ⋅ 65 α mR =bh = 0 ξ 8 , 5 1000 ⋅ ⋅ 65 ⋅ 0,105= 0,095; Аs = b R0b bh=02 8,5 ⋅ 1000 ⋅ 65 2 = 139,8 мм 2. 415 Rs 6 M ξ =1− 3,412 ⋅ 10 1 − 2 α = 1 − m αm = = = 0,095;1 − 2 ⋅ 0,095 = 0,1; 2 ξ = 1 − 1 − 2α 2 m = 1 − 1 − 2 ⋅ 0,095 = 0,1; Rb bh0 8,5 ⋅ 1000 ⋅ 65 R bh ξ 8,5 ⋅1000 ⋅ 65 ⋅ 0,1 = 133,1 мм 2. Аs = b 0 = 5 В500 − 150 415 R 5 В500 − 1502960 × L ⋅ 1000 ξ = 1 − 1 − 2α m =R1bsbh − 0о 1 − 28⋅ ,05,095 = 0⋅,165 ; ⋅ 0,1 2 Аs = R bh о= 8,5 ⋅ 1000 ⋅ 65 ⋅ 0,1= 1332,1 мм .2 3В500 − 200 2960 × Принимают 7Адиаметров с As = 137,5 =мм Rbs 0 =5В500 415 133и,1соответствуюмм . 3В500 − 200 s = 415 Rs 55 5 В500 − 150 2960 × L . щую дополнительную рулонную R bh о 8,5 ⋅ 1000 ⋅ 65 ⋅ 0,1 сетку марки Аs = b 0 = = 133,1 мм 2 . 3В500 − 200 415 как и в крайних пролетах. Rs Сетки раскатывают так же, 5.3. Расчет второстепенной неразрезной балки Расчетная схема и усилия в балке Расчетные нагрузки на 1 п. м второстепенной балки: постоянная − от собственного веса плиты и пола q1 = g(l1 /3)gn = 5,325 · 6,0/3 · 1,0 = 10,65 кН/м; – 83 – 20 . − то же от ребра сечением 0,25 · 0,42(0,5 – 0,08 = 0,42); q2 = b h r gf gn = 0,25 · 0,42 · 25 · 1,2 · 1,0 = 3,15 кН/м; полная постоянная нагрузка qg = q1 + q2 = 10,65 + 3,15 = 13,8 кН/м; временная нагрузка qv = v(l1 /3)γn = 18 ∙ 6/3 ∙ 1,0 = 36,0 кН/м; полная расчетная нагрузка q = qg + qv = 13,8 + 36,0 = 49,8 кН/м. Расчетная схема второстепенной балки – неразрезная многопролетная балка. Расчётный пролёт второстепенных балок принимают равным расстоянию в свету между главными балками l0 = 6,0 – 0,3 = 5,7 м, а при опирании на наружные стены – расстоянию от центра площадки опирания на стену до грани главной балки l01 = 6,0 – 0,30/2 = 5,85 м (рис. 5.4). Изгибающие моменты определяют как для многопролетной балки методом предельного равновесия с учетом перераспределения усилий. Рис. 5.4. Расчетный пролет крайней второстепенной балки Изгибающий момент в первом пролете: M = ql012/11 = 49,8 · 5,852/11 = 154,93 кН·м. Изгибающий момент на первой промежуточной опоре: M = q[(l01 + l02)/2]2/14 = 49,8 · [(5,85 + 5,7)/2]2/14 = 118,64 кН·м. – 84 – Изгибающий момент в средних пролетах и на средних промежуточных опорах: M = ql02/16 = 49,8 · 5,72/16 = 101,13 кН·м. Отрицательные моменты в средних пролетах определяют по огибающей эпюре моментов. Огибающая эпюра моментов строится для двух схем загружения: полная нагрузка q в нечетных пролетах и условная нагрузка qg + 0,25qv в четных пролетах; полная нагрузка q в четных пролетах и условная нагрузка qg + 0,25qv в нечетных пролетах. Условная нагрузка qу = 13,8 + 0,25 · 36,0 = 22,8 кН/м. Изгибающий момент от условной нагрузки в первом пролете: M = qy l012/11 = 22,8 · 5,852/11 = 70,94 кН·м. Изгибающий момент от условной нагрузки в средних пролетах: M = qy l02/16 = 22,8 · 5,72/16 = 46,3 кН·м. Отрицательный изгибающий момент во втором пролете: M = –(118,64 + 101,13)/2 + 46,3 = –63,6 кН·м. Отрицательные изгибающие моменты в следующих пролетах: M = –101,13 + 46,3 = –54,83 кН·м. Огибающая эпюра изгибающих моментов во второстепенной балке представлена на рис. 5.5. Рис. 5.5. Огибающая эпюра изгибающих моментов во второстепенной балке – 85 – Поперечные силы во второстепенной балке: − на крайней опоре Q1 = 0,4ql01 = 0,4 · 49,8 · 5,85 = 116,53 кН; − на первой промежуточной опоре слева Q2,лев = 0,6ql01 = 0,6 · 49,8 · 5,85 = 174,8 кН; − на первой промежуточной опоре справа и других опорах Q2,прав = 0,5ql01 = 0,5 · 49,8 · 5,7 = 141,93 кН. Расчет второстепенной балки по первой группе предельных состояний. Характеристики прочности бетона и арматуры Бетон тяжелый класса В15; расчетное сопротивление бетона на сжатие Rb = 8,5 МПа. Арматура продольная класса А400, Rs = 355 МПа, поперечная А400, Rsw = 285 МПа. Проверка высоты сечения балки Высоту сечения балки проверяют по опорному моменту М = 118,64 кН·м при ξ = 0,35, поскольку он определен с учетом образования пластического шарнира. 118,64 ⋅ 106 M = 439,5 мм. = 0,289Rb b 0,289 ⋅ 8,5 ⋅ 250 Минимальная высота балки h = h0 + a = 439,5 + 50 = 489,5 мм. M 154,93 ⋅10 6 Принятая высота α m = балки2500 = мм достаточная. = 0Рабочая ,0431; высота балки 2 Rbhb0′f=h0500 8–,550 ⋅ 2000 ⋅ 460 в опорном сечении = 450 мм. h0 = Расчет прочности по сечениям, нормальным к продольной оси ξ = 1 − 1 − 2α m = 1 − 1 − 2 ⋅ 0,0431 = 0,0441 . В пролетах сечение второстепенной балки тавровое – полка в сжатой зоне. Расчетная ширина свеса полки в каждую сторону от R b′f h0о 8,5 ⋅ 2000 ⋅ 460 ⋅ 0,0441 ребра должна более половины расстояния свету = b не = = 971в,44 мм 2 .между Аs быть R 355 s второстепенными балками и не более 1/6 рассчитываемого пролета. В элементах с полкой толщиной h′f < 0,1h без поперечных ребер вводимая ширина каждого свеса не должна превышать 6h′f. В нашем случае при h′f = 80 > 0,1h = 0,1 ∙ 500 величина свесов, вводимых в расчет, в каждую сторону должна быть не более (2000 – 250)/2 = 875 мм и не более l2 /6 = 6000/6 = 1000 мм и, следовательно, полная ширина полки, вводимая в расчет, равна b′f = 2000 мм. – 86 – 118,64 ⋅ 106 6 M h0 = 118,64 ⋅ 10 = 439,5 M = h0 = 0,289 Сечение в первом пролете: Rb b = 0,289 ⋅ 8,5 ⋅ 250 = 439,5 0,289Rb b 0,289 ⋅ 8,5 ⋅ 250 М = 154,93 кН·м, h0 = 500 – 40 = 460 мм. M 154,93 ⋅1066 6 α m = M M 2 = 118 154 ⋅10 2 = 0,0431; ,64,93 ⋅ 10 = 0,,0431 439 5 ; h0 = α m =Rb b′f h0=2 =8,5 ⋅ 2000 ⋅ 460 = ,5 ⋅ 2000 460 2 0,289RRbbbb′f h0 0,8289 ⋅ 8,5 ⋅ ⋅250 ξ = 1 − 1 − 2α m = 1 − 1 −6 2 ⋅ 0,0431 = 0,0441 . 154 ⋅1061 − 2 ⋅ 0,0431 = 0,0441 . ξ =M 1M− 1 − 2α =,93 1⋅−10 101 m ,13 =бетона ,0431; ; Высота зоны ==00,0281 ααmmсжатой == = 2 2000⋅ ⋅460 46022 RRbbbbR′f ′bfhbh02′0f h0о88,5,5⋅8⋅2000 ,5 ⋅ 2000 ⋅ 460<⋅ 0h′,0441 = 20,3 80=мм, ′ h о= ∙8460 b0,0441 971,44 мм 2 . Аxs == ξh0R= ,5 ⋅ 2000 ⋅ 460 ⋅ 0f ,= 0441 = 971,44 мм 2 . Аs = Rb s f 0 = 355 следовательно, нижняя проходит в полке, Rsm =граница 355 =11−− 11−−2сжатой 2⋅ 0⋅ ,00281 ,0431зоны ,0441 ξξ==11−− 11−−22αα = =0,00285 .. m и сечение рассчитывается как прямоугольное: ААss == RRbbbb′f′f h00ξо 8,5 ⋅ 2000 ⋅⋅ 460 460⋅⋅00,,0285 0441 971,80 44 мм мм22.. = == 627 355 RRss Принимаем 2 диаметра 25 А400 с As = 982 мм2. 6 M 63,6 ⋅ 10М Сечение в средних пролетах: = 101,13 кН·м, h0 = 460 мм. αm = = = 06,148; 2 M 2 ⋅ 10 6 101 , 13 8,5 ⋅=250 ⋅ 450 α mRb=bh0 M 101 , 13 ⋅ 10 = 0,0281; α m =Rb b′f h02 2 =8,5 ⋅ 20006 ⋅ 460 2 2 = 0,0281; ′ ,5 ⋅ 10 2000 ⋅ 460 M Rb b f h01018,13 = =0,00281 ξα=m1=− 1 − 2α2 m= = 1 − 1 − 2 ⋅ 0,148 ,161;; ′ Rb b f h0 8,5 ⋅ 2000 ⋅ 460 2 ξ = 1 − 1 − 2α m = 1 − 1 − 2 ⋅ 0,0281 = 0,0285 . ξ = 1 − 1 − 2α m = 1 − 1 − 2 ⋅ 0,0281 = 0,0285 . Высота сжатой бетона Rb b′f hзоны 8,5 ⋅ 2000 ⋅ 460 ⋅ 06,161 0ξ 2 А ξ s==1 − 1 R −b2bα 1⋅−2000 2,13 ⋅ 0⋅,⋅10 0281 0,431 0285мм . . ′f = ξ= 1 −8,5101 h M m 460<⋅ 0=h′ ,=0285 0 355 R 6= xm === ξhs 0R= 0,0285 ∙ 460 = 13,1 = 80 мм. 0 , 0281 ; α = ′ ξ b h = 627 ,80 мм 2. 2 А 8,5 ⋅ 101 2000 ,13⋅ 460 ⋅ 102 ⋅ 0f ,0285 b f M s 20 ′ = = 627 Аsα=mR= 8 , 5 ⋅ 2000 ⋅ 460 b h 355 R = 0 , 0281 ; ,80 мм . = b f 0 Rb b′f h0 ξsRbs b8′f,5h⋅022000 0,0285 ⋅355 8,5⋅ 460 ⋅ 2000 ⋅ 460 2 = = 627,80 мм 2. Аs = 355 6 Rs ξ = 1− M 1 − 2α m =63 1 −,6 ⋅110− 26⋅ 0,0281 = 0,0285 . α m 2ξ=диаметра = 220 =⋅ 0,148 Принимаем A1s = мм;2. = 0,0285 . 63 = 1 −M21 − α mА400 = ,16−с⋅ 10 −2 2628 0281 α m =Rb bh0 2 =8,5 ⋅ 250 = 0 ,148; ⋅ 450 2 На отрицательный в6 пролете сечение работает как bb′f bh h0момент 250 ⋅ 450 MRbR 6,5⋅ 10 ⋅ 2000 ⋅ 460 ⋅ 0,0285 0ξ 63,8 α m =Аs =так2 R =как = 0,⋅148 =0 ξ 8,5находится = 627,80 мм 2зоне, . 2 460; ⋅ 0в,0285 ⋅ 22000 прямоугольное, растянутой b b ′f hполка R bh 8 , 5 ⋅ 250 ⋅ 450 355 R = А = ξ = 1b −s 0 1 −s 2Rα m = 1 − 1 − 2 ⋅ 0355 ,148 = 0,161; = 627,80 мм . h0 = 500 – 50 =ξ450 = 1мм. − 1 − 2sα m = 1 − 1 − 2 ⋅ 0,148 = 0,161; Сечение во втором ξ = 1 − 1R − 2bM α hпролете: = 1 − 63 1М −62⋅=10 ⋅ 0–63,6 ,6148 =кН·м. 0,161; 8,5 ⋅,2000 ⋅ 4606 =⋅ 00,161 0ξ b ′f m 2 α = = ′ h0 ξ= 8,5 ⋅63 Аsm = Rb b f2M 2000 ⋅ 2460 ⋅ 0,148 ,161;= 431 мм . 2 ,6 ⋅ 10 8 , 5 ⋅ 250 ⋅ 450 = = 431 мм . Аsα=mR=bRbh = = 0 , 148 ; 355 s0 Rb b′f h0 ξRbs bh 8,5 ⋅ 460 250355 8,502⋅ 2000 ⋅⋅0450 ,1612 2 = = 431 мм . Аs = ξ = 1R−s 1 − 2α m = 1 −355 1 − 2 ⋅ 0,148 = 0,161; ξ = 1 − 1 − 2α m = 1 − 1 − 2 ⋅ 0,148 = 0,161; M 54,83 ⋅10 6 α m = Rb b′f h =ξ 8,5 ⋅ 2000 ⋅2 460 = 0,⋅127 0,161 20 = 431 мм 2. 2 Аs = Rb bh R0b b′f h8=0,5ξ⋅ 2508,⋅5450 ⋅ 2000 ⋅ 460 ⋅ 0,161 355 R = = 431 мм . Аs = s Принимаем 2 диаметра 509 мм2. Rs 18 А400 с As =355 ξ = 1 − 1 − 2α m = 1 − 1 − 2 ⋅ 0,127 = 0,137 – 87 – R bh ξ 8,5 ⋅ 250 ⋅ 450 ⋅ 0,137 = 369 мм 2. Аs = b 0 = 355 Rs 6 M пролете: 54,М 83 = ⋅10–54,83 кН·м. Сечение α в третьем m = M = 54,83 ⋅10 62 = 0,127 8,5 ⋅ 250 α m =Rb bh02 M2 = 54⋅,450 83 ⋅1026 = 0,127 αm R =b bh0 2 8=,5 ⋅ 250 ⋅ 450 2 = 0,127 ; Rb bh0 8,5 ⋅ 250 ⋅ 450 ξ = 1 − 1 − 2α m = 1 − 1 − 2 ⋅ 0,127 = 0,137 ξ = 1 − 1 − 2α m = 1 − 61 − 2 ⋅ 0,127 = 0,137 ; M 1 − 254 83=⋅10 α,,m83 1 −6 616 −= 20,⋅127 0,127 = 0,137 α m = ξR=M1bh−M = 854 10 54 ,⋅83 ⋅102 ⋅=0,0137 ξ 2 , 5 ⋅ 250 ⋅10 450 M 54 , 83 0 b αА = = , 127 6 6 R bh 8 , 5 ⋅ 250 ⋅ 450 α = = = 0,127 ,127 m == 854 = 369 мм 2. 2 02bhM 6= ,0 αsm=m=R bbh 54 ,83 83 10 RbM ,55,⋅83 ⋅54 250 ⋅450 450 137 M ,10 ⋅2⋅10 ,=5 8⋅=250 ⋅ ⋅450 2002ξ8 2=2⋅00,127 bh , 250 ⋅ α =mbR= = 355 R=bh 0 = ,127 = 369 мм . Аsα mα= b 8= ,5 ⋅8250 ⋅450 4502⋅ 4502⋅ 0=,137 2 2ξ 00,127 ,5 ⋅⋅250 250 b sR m R 2 bh 2 355 Rb00bh bh02 8,5 ⋅88250 450 bR 2 = 369 мм . Адиаметра ,,55⋅⋅250 ⋅⋅s450 Принимаем 2 с A = 402 мм . s = Rsbbbh0016=А400 ξ = 1 − 1 − 2αRms = 1 − 1 − 2 ⋅ 355 0,127 = 0,137 −первой 1 − 12α −1− 1 − 12−⋅ 02,127 = 0= ,137 ξ1== 1− 2αα=m1== ⋅ 0,127 ,127 ,137 Сечениеξ = опоре: М = –118,64 кН·м, m ξна 11−−−22промежуточной 00,137 ξ =1ξ1−=−1M α =5911,−− 1⋅110 −−262⋅10⋅−,0127 =,127 0=,137 m m2α 32 − 1 − = 1 − 2 ⋅ 0 =00,137 ,137 двумя сетm ξ = 1 − 1 − 2 α = 1 − 1 − 2 ⋅ 0 , 127 = h0 = 500 – 50 = 450 мм. Опорное сечение армируют 6 = 0,138 α m =Rb bh0M ξ2 =8,5 ⋅m250 ⋅32 450 ⋅ 02,137 59 , ⋅ 10 2 = mRb=Rbh = 369 мм А α ξ00=ξM ,= ⋅ 450 ⋅стержнями bh 85,85⋅5250 450 0,138 ξ28рабочими Rbbbh bh ,⋅5⋅⋅250 ⋅ 250 ⋅ 450 ⋅260,137 ,=137 ками с поперечными в 2 2..соответствии 2 b0bh 59 32 ⋅⋅010 250 ⋅⋅⋅,450 0⋅,137 ,0137 ξ RRR 8 , 250 450 = = 369 мм Аss = 0 355 0 b = = = 369 мм А ⋅ 450 sR =0ξξ2 8=,58⋅,5250 369 мммм . 2. . 2 = ,138 =RR bh =0369 АsАss=α=mRраскатывают ⋅250 250 ⋅450 450⋅⋅200=,балкам. ,137 0= b bh b 355 bh 8 , 5 ⋅ ⋅ 137 355 R с рис. 5.6, которые по главным Ширина s 0 = 8,5 ⋅355 369мм мм2.. сеток 250 ⋅ 450 355 sbs b bh ==369 ААss ==RRsR 0 = 355 R ξ = 1 − 1 − 2 α = 1 − 1 − 2 ⋅ 0 , 138 = 0 , 149 s 355 сеток рассчитываем на R 3,48 m м. Арматуру (0,33 + 0,25)l2 = 0,58 · 6 = ξ = 1 − 1 −s2α m = 1 − 61 − 2 ⋅ 0,138 = 0,149 M 59 , 32 ⋅ 10 изгибающий момент М = –118,64/2 = α59 =⋅10 1⋅10 −66 6–59,32 16 = − 20,⋅138 0,кН·м. 138 = 0,149 α m = ξR=M1bh−M =1 −8259 ,32 ,⋅m 32 M 59 , 32 ⋅ 10 ξ 2 2 , 5 250 ⋅ 450 ⋅ 0 , 149 = 0 , 138 α = = 2 M 59 , 32 10 αА ==mm R=bbbh020 =2 =8=,5 ⋅ 250 ⋅ 45022 =660= 0,=138 α m 0149 ,138401,21 мм 2 αsm =R bh 59 ,32 32 10 M ⋅10 RRRb bh 2ξ= 2⋅= 8 , 5 ⋅ 250 ⋅ 450 0 , 8 , 5 ⋅ 250 ⋅ 450 0 M 59 , ⋅ 8 , 5 ⋅ 250 ⋅ 450 0 2 2 bh 8 , 5 ⋅ 250 ⋅ 450 355 ,138 401;,21 мм Аsαα=mmbR== 0 =8= sb0R 0bh ,=5 ⋅8250 ⋅ 450⋅ 450 2⋅ 0==,149 00,=138 250 b bh b bh022ξ 355 8,,5,55⋅⋅⋅250 250 4502 ⋅450 = = 401,21 мм 2 Аs = R 0 RRsbbbh 8 ⋅ 0 = 1 − 1 − 2 ⋅ 0,138 = 0,149 ξ = ξ1 =− 1 −1 −12−α Rsα m = 1 − 1 − 2355 ,138 = 0,149 ξ 5=В 1 =− 1 −1−−300 2α22m = 1 − 1 − 2 ⋅ ⋅020,138 = 0= ,149,149 ; ,138 ξξ=500 1 − 11−−2m ααmm==11−− 11−−20 2 ⋅ 0⋅ 0,138 = 00,149 3500 18000 × ξ = 1 − 1 − 2 α = 1 − 1 − 2 ⋅ 0 , 138 ,149 20 5В 500 300 m = 1 − 1 − 2 ⋅ 0,138 ==00,149 ξR=bh 1−−200 2,58α,⋅5m 8 А400 ξ0−1ξ− ⋅ 250 ⋅ 450100 83500 250 ⋅ 450 ⋅⋅00,,149 × 18000 22 b0bh bR 20 5 500 300 В = = = 401 , 21 мм А =ξ8,5 8⋅3500 = 401,21 мм Аs 8=А ξ200 bh 250 ⋅ ×450 ⋅ 0100 ,149 sR400 −bh R 2. , 5 ⋅ 250 ⋅ 450 ⋅ 0 , 149 0R bR 18000 0 b ξ bh 8 , 5 ⋅ 250 ⋅ 450 ⋅ 0 , 149 355 = 200 = 401 ,21,мм Аs = bs s0− =АR400 =ξ 8,5355 =401 401 21мм мм2 2 s 100 8 R bh = = = , 21 АА ⋅ 250 ⋅ 450 ⋅ 0 , 149 0 b s 5355 ⋅ 250 ⋅ 450 ⋅ 0,149 401,21 мм22 355 =sRRRbsbh0 ξ ==88,А400 АsRдиаметров 355 Принимаем А 10 с6 As = 503 мм==2 401 и две ,21 соответстмм s =Ms R 355 355 Rs=s 50,565 ⋅ 1020 6 = 0,1175 5 В 500 − 300 α = ,565 ⋅20 102 . M2 350050 5 Вm500 − 300 18000 вующие сетки 8,5×⋅×18000 250 ⋅565 450 bh = = 20 5 В500 −Rb300 0 3500 m500 А 100 8В 400 −−300 200 2026 = 0,1175 5α 300 50 , ⋅ 10 M 2 20 5 500 В − 3500 18000 × 100 8 А400 200 − 8 , 5 ⋅ 250 ⋅ 450 R bh 3500 18000 × α = = = 0,1175 0 b 3500 × 18000 20 500 300 2 100⋅100 200R200 А400 −m500 Сечение8 на 20 55400 ВВ −−b300 А400 8,опорах: 5×⋅×250 450 bh02 3500 3500 18000 100 88Апромежуточных −−200 18000 ξ = 188−АА400 1 −−−2200 α200 1 −62 ⋅ 0100 ,100 1175 = 0,1254 400 m = 1 −h = Мξ== 101,13 500 –⋅ 050 = 450 50=,565 M1 −кН·м, 0−⋅ 10 1 − 2 α 1 1 − 2 ,1175 = 0мм. ,1254 6 m α m =M = ,565 ⋅ 10 2 = 0,1175 21 −50 6 ξ = 1 − 2 α = 1 − 1 − 2 ⋅ 0 , 1175 = 0–50,565 ,1254 кН·м. 8,5,565 ⋅mсетку 250⋅ 10 ⋅ 450 bh 6 α m момент = RMRbh = = 0 , 1175 Расчетный на М = –101,13/2 = 0 одну bM 50 ,565 ⋅ 10 20 ξ= 8,50 26 ⋅= 5⋅ 50 ⋅ ,250 ⋅⋅450 0,01254 565 10 M b αА = , 1175 6 8 , 5 250 ⋅ 450 R bh α = = = 0 , 1175 m = 337,7 мм 2 2 6= 0,1175 2⋅ 10 αsm=m=R bbh ,565 565 M== 5 ⋅8250 Rb02bh ,55⋅50 ⋅50 250 ⋅ 450 450 ⋅ 10 M ⋅,450 2002ξ8,= 2 2⋅ 0,1254 8 , 250 ⋅ bh 0 b 355 R α = = = 0 ,1175 = = 337 А b 6 s50 ,5= ⋅18250 ⋅ −450 ; ,7 мм = ==00,1175 ξ sα = 1mmR −=b bh 1R−b0,565 2α02m −,5 ⋅1250 2 ⋅ 0450 ,1175 ,1254 28 ξ⋅10 bh M 22⋅ 0,1254 = 337,7 мм 2 8 , 5 ⋅ 250 ⋅ 450 R bh 355 R = = А αm = = = 0 , 1175 ; 0 b s 8 , 5 ⋅ 250 ⋅ 450 R bh 0 = 1 −2 1 − 2 ⋅ 0,1175 = 0,1254 ξ R= 1bh−2 s 18−,52⋅bα 355 Rm 250 s ⋅=450 ξ =bξ1 =−01 −1R−bh 2− αξm 15=− = 0= ,1254 1 2 α 1−−1⋅−1450 12−−⋅2⋅002⋅,,1175 ⋅ 0,1175 ,1175 ,1254 ⋅1250 1254 m,= 2; b1 −02α m8 ξ= 1 − = 0,0,71254 = 337 мм Аsξ== 1 − 1 −= 2α = 1 − 1 −02 ⋅ 0 , 1175 ,1254 ξ = 1 − 1 −ξ 2=α1m−R=s 11−− 21α −m 2m⋅ 0=,1175 = 0,1254 ;1175 ==00,1254 1 − 1 − 2 ⋅ 0 , 355 Rb bh0 ξ 8,5 ⋅ 250 ⋅ 450 ⋅ 0,1254 = 337,7 мм22 2 А = Rb bh ξ 0=ξ8,5 8⋅ 250 ⋅ 450 ⋅ 0,1254 Rb0bh ⋅ 250 ⋅ 450 ,1254 ,5,5⋅ 250 ⋅ 450 ⋅ 0⋅ 0,1254 .2 =250=8⋅ 450 = 337 ,7 мм АRssb= 355 ξRRbsbh bhs 0= 8 , 5 ⋅ 0 , 1254 0⋅ξ =. 337 мм А Rbbh bh= ξ 88,,55⋅355 ,7,7мм ⋅250 250 450 ,1254 337⋅⋅0 ,07,1254 мм=2337 Аs = Аs = R=s R ⋅⋅=450 355 bs 00ξ 355 = = 337 , 7 мм22 355 Rs ААss ==RR = = 337,7 мм s 355 R 2 s R Принимаем 7 диаметров 8 А400 с A355 = 352 мм и две соответствуs s ющие сетки 5 В500 − 300 3500 × 18000 20 . 100 . 8 А400 − 300 – 88 – Армирование опорных зон второстепенных балок представлено на рис. 5.6. Раскладка сеток армирования плиты и опорных сеток второстепенной балки показана на рис. 5.7. Рис. 5.6. Армирование опорных зон второстепенной балки сварными сетками (арматура балок условно не показана) Расчет прочности по сечениям, наклонным к продольной оси Проверка по сжатой наклонной полосе Q = 174,8 кН. Qmax = 174,8 ≤ 0,3Rb bh0 = 0,3 · 8,5 · 250 · 450 = = 286875 H = 286,88 кН. Прочность наклонной полосы обеспечена. Диаметр поперечных стержней назначают из условия свариваемости с продольными стержнями d = 25 мм и принимают dsw = 8 мм класса А240. Шаг поперечных стержней для всех приопорных участков по конструктивным условиям не более sw = h0 /2 = 450/2 = 225 мм. Принимаем шаг sw = 150 мм, As = 50,3 мм2. В каждой второстепенной балке устанавливают пространственный каркас, состоящий из двух плоских, при этом Asw = 2 · 50,3 = 101,6 мм2. – 89 – – 90 – Рис. 5.7. Раскладка сеток армирования плиты и опорных сеток второстепенной балки (штриховкой выделены двойные сетки) Определяют интенсивность хомутов: Mb 56,93 ⋅ 10 6 Rsw Asw 170 ⋅ 100,6 c= = =1338 = = 115,15 Н/мм, 31,8 q1 150 sw проверяют условие qsw ≥ 0,25Rbt b = 0,25 · 0,75 · 220 = 41,25 Н/мм. УсRbtучитываютbh02 0,75 ⋅ 250 ⋅ 450 2 ловие выполняется, M следовательно, 56,93 ⋅ 10 6 хомуты полностью = =2 Qb = b = = 42548,6 s max = Q 174800 ся в расчете. Рассчитывают M1338 : c b qsw = Mb = 1,5Rbt bh02 = 1,5 · 0,75 · 250 · 4502 = 56,93 · 106 Н. Rsw Asw 170 ⋅ 100,6 qsw =длину = = 57,6 Устанавливают проекции невыгоднейшего наклонного sw 300 сечения с. Поскольку qsw /Rbt b = 115,15/0,75 · 250 = 0,61 < 2, значение с определяем по формуле Mb 56,93 ⋅ 10 6 70 ⋅ 100,6 c= = =1338 мм < 3h0 = 1350 мм, = 115,15 ,8 ⋅ 100,6 q1 R A 31 150 Mb 56,93 ⋅ 10 6 170 sw sw c= = =1338 = = 115,15 qsw = где q1 = q – 0,5qv = 49,8 36 = 31,8 кН/м. 31,8 q1 sw – 0,5 ·150 Rbt bh02с0 =0,75 ⋅ 250 ⋅ 450=2 900 мм < с. Тогда Принимаем 2h0 = 2 · 450 3 ⋅ 10 6 = = 217 = 42548,6 s max = 6 Q M 174800 338 Rbt bh02 0,75 ⋅ 250 ⋅ 450 2 56 , 93 ⋅ 10 b s = = 217 42,55 кН; = Qb = = = 42548,6 Н = max Q 174800 c 1338 70 ⋅ 100,6 Qsw = 0,75qsw c0 = 0,75 · 115,15 · 900 = 77726,2 Н = 77,7 кН; = 57,6 300 Rsw Asw 170 ⋅ 100,6 qswQ= – = 57 ,6 = 132,25 кН; Q= qc= = 174,8 – 31,8 · 1,338 max s 1 300 w 56,93 ⋅ 10 6 174,8 > Q = 132,25 кН. 170 ⋅ 100,6 Qbc+=QswM =b42,55 = + 132,25 ==1338 = = 115,15 31 ,8 q1 150 Прочность наклонных сечений обеспечена. Проверяют требо- вание 2 Rbt bh02 R 0,75 ⋅ 250170 ⋅ 450 Mb 6,93 ⋅ 10 6 56,93 ⋅ 10 6 ⋅ 100=,6217 мм > s = 150 мм. sw Asw = = 42548,6 s max = = =133 = = 115,15 w c = qsw = Q 1338 31,8 q1 sw 174800 150 Принятый шаг хомутов не превышает максимального значения. 170 ⋅ 100,6 2 шаг поперечR bh 0,75 ⋅ 250 ⋅ 450 2 = 57,6 В средней части второстепенной M b 56,93 ⋅ 10 6балки принимаем = bt 0 = = = мм. = Таким образом, = 42548 ,6 s max интенсивность 300 ных стержней sw2Q =b 300 принятая Q 174800 c 1338 хомутов в пролете равна R A 170 ⋅ 100,6 qsw = sw sw = = 57,6 Н/мм. sw 300 Проверяем условие qsw2 ≥ 0,25Rbt b = 0,25 · 0,75 · 250 = 46,88 Н/мм, условие выполняется. Определяем длину участка l1 с интенсивностью хомутов qsw1. Так как – 91 – Dqsw = 0,75(qsw1 – qsw2) = 0,75(115,15 – 57,6) = = 43,16 Н/мм > q1 = 31,8 Н/мм, значение l1 вычислим по формуле, приняв Qb,min = 0,5Rbt bh0 = 0,5 · 0,75 · 250 · 450 = 42187,5 Н; l1 = = Qmax − (Qb, min + 1,5qsw2 h0 ) − 2h0 = q1 174800 − (42187 + 1,5 ⋅ 57,6 ⋅ 450) − 2 ⋅ 450 = 2048 мм. 31,8 Принимаем длину участка с шагом хомутов sw1 = 150 мм равной 2,1 м. В средних пролетах второстепенной балки поперечная сила Q23 = 141,93 кН. Расчет выполняется аналогичным образом. – 92 – 6. РАСЧЕТ КРАЙНЕЙ КОЛОННЫ 6.1. Определение усилий в колонне В курсовом проекте принята самонесущая кирпичная стена толщиной 510 мм на ленточном фундаменте с наружным утеплением. Здание четырехэтажное с высотой первого этажа 6,0 м, последующих – 4,8 м. Сечение колонн b×h = 400×400 мм. Определение продольных сил от расчетных нагрузок Вертикальная нагрузка на колонну собирается с грузовой площади. Грузовая площадь крайней колонны при сетке колонн 6×6 м A= l1 × l2 = 3 ⋅ 6 = 18 м2. 2 Постоянная нагрузка от перекрытия одного этажа с учетом коэффициента надежности по ответственности здания γn = 1,0 и с учетом собственного веса ригеля Grig = br hr lr r gf /2 = 0,3 · 0,6 · 5,4 · 25 · 1,1/2 = 13,365 кН; Ng1 = (gA + Grig) gn = (5,675 · 18 + 13,365) · 1,0 = 115,52 кН. Постоянная нагрузка от веса покрытия при расчетном весе кровли и плит 5,25 кН/м2: Ng2 = (gA + Grig) gn = (5,25 · 18 + 13,365) · 1,0 = 107,86 кН. Постоянная нагрузка от собственного веса колонны от верха до перекрытия первого этажа Н = 4,8 · 3 = 14,4 м с учетом коэффициента надежности по ответственности здания γn = 1,0 Ng3 = r H b h gf gn = 25 · 14,4 · 0,4 · 0,4 · 1,1 · 1,0 = 63,36 кН. Временная нагрузка: от перекрытия одного этажа Nv = Av gn = 18 · 18 · 1,0 = 324,0 кН, – 93 – в том числе длительная Nv1 = Av1 gn = 18 · 14,4 · 1,0 = 259,2 кН. Временная нагрузка от снега на покрытие (IV снеговой район): Ns = ASg μγn = 18 ∙ 2,4 ∙ 1 ∙ 1,0 = 43,2 кН, в том числе длительная Nsl = 43,2 ∙ 0,5 = 21,6 кН. Продольная сила в колонне первого этажа от полной нагрузки на уровне перекрытия первого этажа: N1 = 3Ng1 + Ng2 + Ng3 + 3Nv + Ns = = 3 ∙ 115,52 + 107,86 + 63,36 + 3 ∙ 324,0 + 43,2 = 1532,98 кН. Продольная сила в колонне первого этажа от полной нагрузки на уровне фундамента: Nф = N1 + r H1b h gf gn = 1532,98 + 25 ∙ 6,0 ∙ 0,4 ∙ 0,4 ∙ 1,1 ∙ 1,0 = 1559,38 кН. Продольная сила в колонне первого этажа от постоянной и временной длительной нагрузки на уровне перекрытия первого этажа N1l = 3Ng1 + Ng2 + Ng3 + 3Nvl + Nsl = = 3 ∙ 115,52 + 107,86 + 63,36 + 3 ∙ 259,2 + 21,6 = 1319,98 кН. Определение изгибающих моментов в колонне Опорный изгибающий момент в ригеле в стыке с крайней колонной распределяется между верхней и нижней колоннами пропорционально их погонным жесткостям. При одинаковой длине и равных сечениях верхней и нижней колонн опорный момент ригеля распределяется между ними поровну. В средней колонне распределяется разность опорных моментов в стыке ригеля с колонной слева и справа ∆M = M21 – M23 также пропорционально погонным жесткостям. Максимальный опорный изгибающий момент в стыке ригеля с крайней колонной будет при загружении 1 + 2 М12 = 197,72 кН·м, и он распределяется в узле поровну между низом и верхом колонны пропорционально погонным жесткостям верхней и нижней колонн. При одинаковых размерах сечения колонн (сократив на EI) погонная жесткость колонны второго этажа равна i2 = 1/4,8 = 0,2083. Погонная жесткость колонны первого этажа при жестком защемлении – 94 – в фундамент равна i1 = 1,33 · 1/6 = 0,2217. Изгибающий момент распределится между колоннами следующим образом: в колонне второго этажа М i 197,72 0,2083 М 1в 12 2 95,78 кН·м; i1 i2 0,2083 0,2217 в колонне первого этажа М i 197,72 0,2217 М 1н 12 1 101,94 кН·м. i1 i2 0,2083 0,2217 Изгибающий момент в колонне первого этажа в месте заделки в фундамент определяют умножением момента в верхнем сечении колонны на коэффициент 0,5: М1ф = 101,94 · 0,5 = 50,97 кН·м. Изгибающий момент в опорном сечении ригеля от постоянной и временной длительной2нагрузок (из расчета ригеля): 2 М 12l = −(αq g + βqvl )l0 = −(0,033 ⋅ 40,65 + 0,042 ⋅ 86,4)5,8 = 167,2 кН ⋅ м, М 12l = −(αq g + βqvl )l02 = −(0,033 ⋅ 40,65 + 0,042 ⋅ 86,4)5,8 2 = 167,2 кН ⋅ м, α,4qq⋅gg6+,+0ββ⋅1qq,vl0vl ))=ll020286==,4−−((кН·м. 033⋅⋅40 40,,65 65++ 00,,042 042⋅⋅86 86,,44))55,,8822 ==167 167,,22 кН кН⋅⋅м, м где qvl = ϑl ⋅ М ((α 00,,033 lМ ⋅12γlln ===−−14 2 12 qvl Изгибающий = ϑl ⋅ l 2 ⋅ γ n = 14момент ,4 ⋅ 6,0 ⋅1,М 0 = 86 , 4 распределится между колоннами сле12l М qvll ⋅==i2ϑ 167 ,2083 дующим образом: ϑ=ll ⋅⋅ll,2 ⋅ 0γ,2 14 86 =⋅=014 ,,44⋅⋅66,,00=⋅⋅1180 ,,00,99 == 86 ,,44⋅ м; 22 ⋅⋅ γ М 1вМ=12l ⋅q12 кН i2vl 167 ,nn2083 М 1вв = = = 80,99 кН ⋅ м; i1 +второго i2 + 0,2217 0,2083 колонне этажа i1 + i2 0,2083 + 0,2217 М 12ll ⋅⋅ii22 167,2 ,2⋅⋅00,,2083 2083 167 в в М11 == М 12 80,,99 99 кН кН ⋅⋅м; м; М == == 80 2083++ 00,,2217 2217 М 12l ⋅ i2 ii11167 ⋅ 0,002217 ++⋅ii022,,22217 ,,2083 н М i ⋅ 167 , 2 М 1 =12l 2 = = = кН ,19⋅ м. кН ⋅ м. М 1нв =колонне = 86,1986 первого этажа + 0,2217 0,2083 i1 + ii12 + i2 0,2083 + 0,2217 М 12ll ⋅⋅ii22 167 167,,22⋅⋅00,,2217 2217 М11нн == М 12 86,,19 19 кН кН ⋅⋅м. м. М == == 86 2083++ 00,,2217 2217 ii11 ++ ii22 00,,2083 Изгибающий момент на нижнем конце колонны в месте заделки в фундамент от длительной нагрузки М1фl = 86,19 · 0,5 = 43,095 кН·м. Наиболее нагруженным является сечение колонны первого этажа с большим изгибающим моментом в сечении стыка с ригелем. – 95 – 6.2. Расчет продольной арматуры колонны Характеристики прочности бетона и арматуры Бетон тяжелый класса В20. Расчетное сопротивление при сжатии Rb = 11,5 МПа; при растяжении Rbt = 0,9 МПа; начальный модуль упругости бетона Eb = 27500 МПа; арматура продольная рабочая класса А400, расчетное сопротивление Rs = 355 МПа; модуль упругости Es = 200000 МПа. Общие положения расчета Колонны производственных зданий работают в условиях внецентренного нагружения. Значение эксцентриситета продольной силы относительно центра тяжести приведенного сечения е0 принимают равным значению эксцентриситета, полученного из статического расчета, но не менее случайного эксцентриситета еа. Величина случайного эксцентриситета принимается не менее: 1/600 длины элемента или расстояния между его сечениями, закрепленными от смещения; 1/30 высоты сечения; 10 мм. Во всех случаях эксцентриситеты е0 определяют с учетом влияния прогиба элемента. Влияние прогиба элемента на момент продольной силы (или ее эксцентриситет е0) учитывают, как правило, путем расчета конструкции по деформируемой схеме, принимая во внимание неупругие деформации бетона и арматуры, а также наличие трещин. Допускается производить расчет конструкции по недеформируемой схеме, а влияние прогиба элемента учитывать путем умножения моментов на коэффициенты ηv, ηh в соответствии с формулой M = Mvηv + Mhηh + Mi, (6.1) где Mv – момент от вертикальных нагрузок, не вызывающих заметных горизонтальных смещений концов; ηv – коэффициент, принимаемый равным: при податливой заделке – 1,0; при жесткой заделке – по формуле (6.2); Mh – момент от нагрузок, вызывающих горизонтальное смещение концов; ηh – коэффициент, определяемый по формуле (6.2); Mi – момент от вынужденных горизонтальных сме- – 96 – щений концов (т. е. смещений, не зависящих от жесткости элемента, например, от температурных деформаций перекрытий и т. п.). Значение коэффициента ηv(h) при расчете конструкций по недеформируемой схеме находится по формуле ηv ( h ) = 1 , N cr = π2 D ; l02 3 D = E(6.2) b bh 1− N N cr где Ncr – условная критическая сила, определяемая по формуле ηv ( h ) = 1 0,0125 ϕ ( 0,3 + δ e ) ( 2 ′ h −a 0 − a ′ (6.3) 0,175 ,μαN=crА=+πА2D⋅ E,; s .D =ME1b=bhM3 + N0h,0125 M +0 N ; +M 1 =μα ϕ ( 0,32+ δ e ) h bh0l0 Eb N cr 1− N l0 – расчетная длина элемента, для коэффициентов ηv и ηh (соответственно для вертикальной и горизонтальной нагрузок). Расчетная h − a′ h − a′ А + А′ E s M 1 = M + N 0 . M1 = M + N 0 ; = ⋅ равной: длина l0 μα принимается bh0 Eb 2 2 1) при вычислении коэффициентов ηv, а также при расчете элемента на действие продольной силы со случайным эксцентриситетом: − для элементов с шарнирным опиранием на двух концах – 1,0l; − с шарнирным опиранием на одном конце, а на другом конце: с жесткой заделкой – 0,7l; с податливой заделкой – 0,9l; − с заделкой на двух концах: жесткой – 0,5l; податливой – 0,8l; − с податливой заделкой на одном конце и с жесткой заделкой на другом – 0,7l; 2) при вычислении коэффициента ηh: − для элементов с шарнирным опиранием на одном конце, а на другом конце: с жесткой заделкой – 1,5l; с податливой заделкой – 2,0l; − с заделкой на двух концах: жесткой – 0,8l; податливой – 1,2l; − с податливой заделкой на одном конце и с жесткой заделкой на другом – l; − с жесткой заделкой на одном конце и незакрепленным другим концом (консоль) – 2,0l. Здесь l – расстояние между концами элемента; D – жесткость железобетонного элемента в предельной стадии, определяемая для элементов прямоугольного сечения с арматурой, расположенной – 97 – у наиболее сжатой и у растянутой (менее сжатой) грани элемента по формуле (h) = 1 1− N N cr , N cr = π2 D ; l02 D = Eb bh 3 ( ) 0,0125 + 0,175μα h0 − a′ 2 ; ϕ ( 0,3 + δ e ) h (6.4) φℓ – коэффициент, учитывающий влияние длительного действия h − a ′ элемента и равный h − a′ А + А′ E s нагрузки на прогиб M 1 = M + N 0 ; = ⋅ . M1 = M + N 0 bh0 Eb 2 2 не более 2; φ = 1 + M /M но ℓ 1ℓ (6.5) 1 М1 и М1l – моменты внешних сил относительно оси, нормальной плоскости изгиба и проходящей через центр наиболее растянутого 1 π2 D 0,0125 + 0 или наименее сжатого стержня арматуры, от всех , соответственно ηv ( h ) = N cr = 2 ; D = Eb bh 3 l0 нагрузок и от действия постоянных и длительных нагрузок; δе – ко1− N N cr ϕ ( 0,3 + δ e ) эффициент, принимаемый равным е0 /h, но не менее 0,15; μα = А + А′ E s ⋅ . bh0 Eb M1 = M + N h0 − a ′ ; 2 M 1 = M + N ( ) При 1гибкости элемента l0 /i < 14 (для прямоугольныхhсечений − a′ 0,0125 π2 D + 0,175μα 0 Eb1,0. bh 3 , принимать ηvl( h/h N cr = 2 ; ηD = = ) = < 4) можно 0 , 3 h ϕ + δ ( ) 0 v(h) l e 1− N N cr 0 2 Подбор арматуры h − a ′ высоту сечеАЗадаются + А′ E s значениями аh0и− a ′ и вычисляют рабочую M 1 = M + N 0 ; μα = ⋅ . M1 = M + N 2 ния bh h0 0= hE–b a. В зависимости2 от рассчитываемого сечения колонны определяют ее расчетные длины l0 для вычисления коэффициентов ηv и ηh. Проверяют условие l0 /h > 4, если условие выполняется, то необходимо учитывать прогиб колонны. Усилия от всех нагрузок равны M = Mv + Mh; N = Nv + Nh. При этом е0 = М/N. 1 h − a′ 2 0,0125 π2 D 3 0,175проходящей +оси, μα 0 Eb1lbhотносительно , Nмоменты ηv ( h ) Определяют = ;M1Dи= M cr = 2 ϕ ( 0,3 + δ e ) h l0 − N N cr через 1центр тяжести наименее сжатой (растянутой) арматуры, по формуле h − a′ h − a′ А + А′ E s . (6.6) M 1 = M + N 0 ; μα = ⋅ . M1 = M + N 0 ( ) bh0 Eb 2 2 По формуле (6.5) рассчитывают коэффициенты φℓ и δе. Для вычисления жесткостей в первом приближении задаются коэффициентом армирования μ = 0,008…0,012 и по формуле (6.4) вычисляют жесткость D. Затем находят критическую силу по формуле (6.3) и коэффициенты ηv и ηh по формуле (6.2) от вертикальной и горизонтальной нагрузок соответственно. – 98 – h0 − 2 Расчетный момент с учетом прогиба вычисляют по формуле (6.1). Сечение с симметричной арматурой Симметричное армирование используется в колоннах внутренних рядов. Требуемое количество симметричной арматуры определяется в зависимости от относительной величины продольной силы αn = N : Rb bh0 As = As′ = 1) при αn ≤ ξR Rb bh0 α m1 − αn (1 − α n / 2 ) ; ⋅ 1− δ Rs α n (1 − ξ R ) + 2α s ξ R R bh α − ξ(1 − ξ / 2 ) As = As′ = b N0 ⋅ m1 ) m1, − αn (1 − α (6.7) Rb,bh0ξ =α m1 − αn (1R− α n / 2α N 2α −=δA=s′ = n / 2) α n = Rs : A1s α ; ⋅ A = 1A−′ ξ=R +b bh 0s : ; ⋅ n s s Rb bh0 1 R − δ s R bh 1− δ R b 2) при αn > ξR N αn = : Rb bh0 0 s α (1 − ξ ) + 2α ξ R bh α − ξ(1 − ξ / 2 ) ξ R ) + 2α s ξ R As = As′ = b 0 ⋅ Am1= A′ = Rb bh0 ,⋅ α mξ1 =− ξ(n1 − ξ / 2R ) , ξ s= Rα ,n (1 −(6.8) , 1 / 2 − α ( ) RRbsbh0 αs m1 −1sα nδ n 1 2 − − ξ + α R s 1 − ξ R + 2α s Rs ; 1− δ ⋅ As = As′ = 1− δ Rs где ξ – относительная высота сжатой зоны, определяемая по формуле As = As′ = Rb bh0 α m1 − ξ(1 − ξ / 2 ) , ⋅ 1− δ Rs ξ= α n (1 − ξ R ) + 2α s ξ R , 1 − ξ R + 2α s (6.9) где значение αs допускается принимать равным αs = α m1 − ξ1 (1 − ξ1 / 2 ) 1− δ при ξ1 = (αn + ξR)/2, но не более 1,0. В формулах (6.7)–(6.10): Ne − α R Rb bh02 αs = α m1 − ξ1 (1 − ξ1 / 2 ) 1− δ As′ = α m1 = Rsc (h0 − a ′) M + N ( h0 − a′) / 2 Rb bh02 α m1 = M + N ( h(6.10) 0 − a ′) / 2 Rb bh02 , δ= a′ . h0 ξ R Rb bh0 − N + As′ , Rs a′ (6.11) , δ = .. h0 ; As = Далее вычисляют фактический коэффициент армирования µ и ξ R bh − N Ne − α R Rсbранее bh02 принятым, сравнивают значительная, то расAs′ , As′ = ; As = R b и0 если+ разница ′ Rs Rsc (h0 − a ) чет повторяют с новым значением µ. Сечение с несимметричной арматурой Несимметричное армирование используется в колоннах крайних M + N ( h0 − a′) / 2 α m1 − ξ1 (1 − ξ1 / 2 ) a′ рядов. Площади сечения сжатой и растянутой Sα арматуры, соот, δ= . α s = S′ m1 = 2 h 1− δ R bh 0 b 0 ветствующие минимуму их суммы, рассчитываются по формулам: As′ = Ne − α R Rb bh02 ; Rsc (h0 − a ′) – 99 – As = ξ R Rb bh0 − N (6.12) + As′ , Rs αs = α m1 − ξ1 (1 − ξ1 / 2 ) 1− δ As′ = Ne − α R Rb bh02 ; Rsc (h0 − a ′) α m1 = As = M + N ( h0 − a′) / 2 Rb bh02 , δ= a′ . h0 ξ R Rb bh0 − N + As′ , Rs (6.13) где αR и ξR – определяют по табл. 5 и принимают не более соответственно 0,4 и 0,55. Таблица 5 Значения ξR и αR в зависимости от класса арматуры Класс арматуры А240 А300 А400 А500 В500 Значение ξR 0,612 0,577 0,531 0,493 0,502 Значение αR 0,425 0,411 0,390 0,372 0,376 e = M/N + (h0 – a′)/2. При отрицательном значении As, вычисленном по формуле (6.13), площадь сечения арматуры S принимается минимальной по конструктивным требованиям (табл. 6), но не менее величины As , min = N (h0 − a ′ − e ) − Rbbh (h / 2 − a ′) . Rsc (h0 − a ′) (6.14) Таблица 6 (N − Rbba′)2 внецентренно As′ = ( Nпроцент − Rb ba′) −армирования − N ( N − 2 Rb bh0 + 2 Rb be) / Rsc ; Минимальный сжатых колонн N − Rb bh Условия µ ,% As′ = работы −арматуры As , min ξRb bh0 − N + Rsc As,s,min fact Rsc A = , Арматура во внецентренно сжатых элементах: s Rs 1) при l0 /i < 17 (для прямоугольных сечений – при l0 /h ≤ 5) 0,10 2) 17 < l0 /i ≤ 35 (5 < l0 /h ≤ 10) Ne − Rsc As,′ fact (h0 − a ′) ξ = 1 − 1 − 2α , . 3) 35 < l0 /i ≤ 83 (10 < l0 /h ≤ 25) m α m = R bh 2 4) l0 /i > 83 (l0 /h > 25) b 0 0,15 0,20 0,25 Примечание. Для внецентренно сжатых элементов при 17 < l0 /i < 83 зна- чение µs,min (%) можно также определять линейной интерполяцией между значениями 0,10 и 0,25 N (h0 − a ′ − e ) − Rbbh (h / 2 − a ′) As ,Площадь . сечения арматуры S′ определяется: min = Rsc (h0 − a ′) − при отрицательном значении As,min – по формуле As′ = ( N − Rb ba′) − ( N − Rb ba′)2 − N ( N − 2 Rb bh0 + 2 Rb be) / Rsc ; (6.15) − при положительном значении As,min – по формуле N − Rb bh As′ = − As , min ξRb bh0 − N + Rsc As, fact Rsc As = – 100 – , Rs As′ = ( N − Rb ba′) − As , min = (N − Rbba′)2 − N (N − 2 Rbbh0 + 2 Rbbe) )/ .2R−babh′) −Na(h′− N (h0 − a ′N−(eh)0 −− R − /R2bbh a ′b−bhe )(h As , min = .− A s , min . Rsc (h0 − Rasc′)(hA0 s′−=a ′) R (6.16) ξRb bh0 − N + Rsc As, fact As = Rs Если принятая площадь сечения сжатой арматуры As,min значи( N − R ba′) − ( N −2R ba′)2 − N ( N − 2 R bh + 2 Rbe) / R ; ′ =превышает ′ ′ b b b 0 b sc ( ) ( ) ( ) As′ = тельно N −AsR b a − N − R b a − N N − 2 R bh + 2 R be / R ; ее значение, вычисленное по формуле (6.12) (наb b b 0 b sc − a ′) Ne − Rscсечения As,′ fact (h0растяпример, при отрицательном его значении), площадь = 1 − 1 − 2α m , α m = . N − Rb bhможет ξбыть 2 нутой арматуры уменьшена исходя из формулы Rb bh0 N − RAbs′ bh = − As , min R bh − N + R A ξ As′ = −R Ascs , min b 0 sc s, fact ξRAbsbh =0 − N + Rsc As, fact , Rsc Rs (6.17) As = , Rs sc Ne − R A′ (h − a ′) 0 где ξ = 1 − 1 − 2α m ,Neα−m R= A′ sc(hs, fact . −2a ′) sc s, fact Rb0bh 0 ξ = 1 − 1 − 2α m , α m = . 2 Если сжатая арматураRотсутствует или не учитывается в расчете, b bh0 площадь сечения растянутой арматуры определяется всегда только по формуле (6.17), при этом должно выполняться условие αm < αR. Пример расчета В примере приведен расчет колонны только на вертикальную нагрузку. Колонна крайнего ряда и армирование несимметричное. Дано: колонна нижнего этажа рамного каркаса с сечением размерами b = 400 мм, h = 400 мм; a = a′ = 45 мм; бетон класса В30 (Eb = 32500 МПа, Rb = 17 МПа); арматура класса А400 (Rs = Rs′ = 355 МПа); продольная сила и изгибающие моменты в опорном сечении от вертикальных нагрузок: всех N = 1532,98 кН, M = 101,94 кН·м, постоянных и длительных Nl = 1319,98 кН, Ml = 86,19 кН·м; высота этажа l = 6,0 м. Поскольку рассматриваемое сечение опорное у консоли и колонна у этой опоры имеет податливую заделку и жесткую в заделке в фундамент, коэффициент ηv = 1,0 и увеличения изгибающего момента вследствие гибкости колонны не будет. Рабочая высота сечения h0 = h – a = 400 – 45 = 355 мм Рис. 6.1. Сечение колонны (рис. 6.1). – 101 – , Площади сечения сжатой и растянутой арматуры, соответствующие минимуму их суммы, находятся по формулам: As′ = Ne − α R Rb bh02 1532,98 ⋅ 10 3 ⋅ 221 − 0,39 ⋅ 17 ⋅ 400 ⋅ 355 = 3070 мм 2 , = Rsc (h0 − a ′) 355(355 − 45 ) где αR = 0,39 и ξR = 0,531 определяются по табл. 5; ξ R Rb bh0 − N 0,531 ⋅17 ⋅ 400 ⋅ 355 − 1532980 2 + As′ + = (h0 – a′)/2 = 101,94/1532,98 + 3070 e = M/N + = 2363 мм . 3 Rs R bh 2 1532,98 355 Ne − α ⋅ 10 ⋅ 221 − 0,39 ⋅ 17 ⋅ 400 ⋅ 355 R + b (0,355 0 As′ = = – 0,045)/2 = 0,221 м = 221 мм. = 3070 мм 2 , Rsc (h0 − a ′) 355(355 − 45 ) As = Принимаем 4 D 32 с A′s = 3217 мм2. As = ξ R Rb bh0 − N 0,531 ⋅17 ⋅ 400 ⋅ 355 − 1532980 + As′ = + 3070 = 2363 мм 2. Rs 355 Принимаем 4 D 28 с As = 2463 мм2. Процент армирования сечения μ = 3070 · 100/4002 = 1,92 %. Для колонн первого и второго этажей можно было назначить сечение размером b×h = 400×600 мм или принять класс бетона по прочности на сжатие В40. 6.3. Примеры конструирования типовых колонн Колонны выполняются по серии 1.420-35.90 «Конструкции многоэтажных производственных зданий с сетками колонн 6×6 и 9×6 м под нагрузки соответственно 2500 и 1500 кг/м2». В пособии приведены примеры конструирования колонн с обозначениями из типовых проектов. Опалубочные размеры колонн первого и второго этажей сечением 400×400 м при их высоте 4,8 м представлены на рис. 6.2 и 6.3. Опалубочные размеры колон первого и второго этажей сечением 400×600 м при их высоте 4,8 м приведены на рис. 6.4 и 6.5. Конструкция концевых участков колонн – на рис. 6.6. На рис. 6.7–6.9 представлен пространственный каркас колонны в сборе, на рис. 6.10 – армирование концевых участков колонн. – 102 – – 103 – Рис. 6.2. Опалубочные размеры средней колонны первого и второго этажей сечением 400×400 мм – 104 – Рис. 6.3. Опалубочные размеры крайней колонны первого и второго этажей сечением 400×400 мм – 105 – Рис. 6.4. Опалубочные размеры средней колонны первого и второго этажей сечением 400×600 мм – 106 – Рис. 6.5. Опалубочные размеры крайней колонны первого и второго этажей сечением 400×600 мм Рис. 6.6. Концевые участки колонн – 107 – Рис. 6.7. Пространственный каркас крайней колонны: 1 – рабочие угловые стержни продольной арматуры; 2 – рабочие промежуточные стержни продольной арматуры; 4 – хомуты; 6, 7 – каркасы с наклонной арматурой консоли; 8 – сетки косвенного армирования стыковой зоны колонны; 9 – сетки косвенного армирования концевого участка колонны; 11 – арматура консоли; 15 – крестовое соединение продольных стержней (см. рис. 6.10) для обеспечения положения стержней в момент бетонирования; 18 – центрирующая пластина – 108 – – 109 – Рис. 6.8. Армирование консолей крайних колонн: 1 – концевой; 2 – промежуточной; 4 – хомуты; 6, 7 – наклонная арматура консоли; 11 – закладная деталь консоли; 13 – арматура консоли; 17 – металлические пластины – 110 – Рис. 6.9. Армирование консолей средней колонны: 5 – концевой; 6 – промежуточной; 4 – хомуты; 6, 7 – наклонная арматура консоли; 11 – закладная деталь консоли – 111 – Рис. 6.10. Армирование концевых участков колонн 7. ПРОЕКТИРОВАНИЕ ФУНДАМЕНТОВ ПОД КОЛОННЫ 7.1. Общие положения Для проектирования фундамента необходимо знать состав грунтов под подошвой фундамента, их расчетное сопротивление R0, а также класс бетона по прочности на сжатие и класс арматуры и соответствующие им расчетные сопротивления Rb, Rbt, Rs (табл. П2 и П6 приложения). Расчет выполняют на возможные три расчетные сочетания усилий (Mmax, N, Q; Mmin, N, Q; Nmax, M, Q) в колонне в месте ее заделки в фундамент. Площадь подошвы фундамента определяют по нормативным усилиям, которые получают путем деления расчетных значений усилий на усредненный коэффициент надежности по нагрузке γf = 1,15. При этом к каждому сочетанию усилий необходимо добавлять усилия от фундаментных балок, стеновых панелей, фундаментных блоков в случае их наличия с коэффициентом надежности по нагрузке γf = 1,0. Фундаменты под колонны многоэтажных промышленных зданий возводят монолитными или сборными из бетонов класса В15…В20. Все размеры фундаментов принимают кратными 300 или 100 мм из условия изготовления с применением инвентарной щитовой опалубки. Общий вид монолитного фундамента со всеми размерами, которые необходимо определить в курсовом проекте, представлен на рис. 7.1. Высота фундамента h назначается с учетом глубины заложения и размеров подошвы. – 112 – 7.2. Определение геометрических размеров фундамента Определение размеров стакана Определение геометрических размеров фундамента начинают с установления размеров стакана под сборную колонну. Для этого вначале вычисляют максимальное значение эксцентриситета продольной силы е = М/N из трех комбинаций усилий. Глубина стакана dp принимается на 50 мм больше глубины заделки колонны dc, но не менее чем по условиям заделки рабочей арматуры колонн, указанной в табл. 7. В табл. 8 приведены унифицированные размеры подколонников под стаканы. ±0,000 d h 50 dc dp 75 45° 50 50 hpl h1 h2 h3 hcf 75 hc lcf l2 l1 l pmax b1 b bcf bc b2 pmin Рис. 7.1. Конструкция фундамента с эпюрой реактивного давления грунта – 113 – Таблица 7 Минимальная заделка рабочей арматуры колонн в стакан фундамента Глубина заделки рабочей арматуры d при проектном классе бетона В15 В20 Класс рабочей арматуры Колонна A400 Прямоугольного сечения 30d (18d) 25d (15d) A300 Прямоугольного сечения 25d (15d) 20d (10d) d – диаметр арматуры. Значения в скобках относятся к сжатой рабочей арматуре. Таблица 8 Типы и унифицированные размеры подколонников под колонны Тип Сечение Размеры подкоколонн сечения лонни(мм) (мм) ков 300×300 Размер стакана, мм Глубина (мм) понизу поверху Объем стакана, м 700 400×400 450×450 0,13 700 500×400 550×450 0,16 400×400 800, 900 500×500 550×550 0,22; 0,25 500×400 800 600×500 650×550 400×300 500×500 600×400 А Б 900×900 1200×1200 в плане, 1×b 0,26 800, 900 600×600 650×650 0,31; 0,35 800, 900 700×500 750×550 0,3; 0,34 600×500 800 700×600 750×650 0,36 700×400 950 800×500 850×550 0,41 900, 950 900×500 950×550 0,44; 0,46 900 900×600 950×650 800×400 800×500 В 1500×1200 0,52 Определение размеров подошвы и глубины заложения фундамента Согласно указаниям СП 22.13330.2011 «Основания зданий и сооружений» и СП 50-101–2004 «Проектирование и устройство оснований и фундаментов зданий и сооружений» основные размеры фундаментов мелкого заложения назначаются со следующими ограничениями. Давление на грунт у края подошвы внецентренно нагруженного фундамента (вычисленное в предположении линейного распре- – 114 – деления давления под подошвой фундамента при нагрузках, принимаемых для расчета оснований по деформациям), как правило, должно определяться с учетом заглубления фундамента в грунт и жесткости надфундаментных конструкций. Краевое давление при действии изгибающего момента вдоль каждой оси фундамента не должно превышать 1,2R и в угловой точке – 1,5R, а среднее давление pm = Nn /lb ≤ R (здесь R – расчетное сопротивление грунта основания, определяемое в соответствии с [9; 10]). При трапециевидной эпюре давлений с отношением краевых давлений pmin /pmax ≥ 0,25 эксцентриситет вертикальной нагрузки на фундамент равен e ≤ l/10, где l – размер подошвы фундамента в направлении действия момента. Краевые давления р, кПа, при относительном эксцентриситете e/l ≤ 1/6 вычисляют по формуле ([10] п. 5.5.28) p = N/A + γmt d ± M/W, (7.1) где N – сумма вертикальных нагрузок, действующих на основание, кроме веса фундамента и грунта на его обрезах, и определяемых для случая расчета основания по деформациям, кН; А – площадь подошвы фундамента, м2; γmt – средневзвешенное значение удельных весов тела фундамента, грунта и пола, расположенных над подошвой фундамента; принимают равным 20 кН/м3; d – глубина заложения фундамента, м; М – момент от равнодействующей всех нагрузок, действующих по подошве фундамента, найденных с учетом заглубления фундамента в грунте и перераспределяющего влияния верхних конструкций или без этого учета, кН·м; W – момент сопротивления площади подошвы фундамента, м3; е – эксцентриситет нагрузки по подошве фундамента, м, определяемый по формуле e = M/(N + γmtdlb). (7.2) Коэффициент надежности по нагрузке γf принимают при расчете оснований: − по первой группе предельных состояний (по несущей способности) – по СП 20.13330.2011; − по второй группе предельных состояний (по деформациям) – равным единице. – 115 – Глубина заложения фундаментов должна приниматься с учетом: − назначения и конструктивных особенностей проектируемого сооружения, нагрузок и воздействий на него; − существующего и проектируемого рельефа застраиваемой территории; − инженерно-геологических условий площадки строительства; − глубины сезонного промерзания грунтов. Минимальная глубина заложения подошвы фундамента dmin, исходя из условия минимальной высоты фундаментов зданий hmin = dp + 0,2 м, составляет dmin = h + 0,15 м. Здесь dp – глубина стакана; 0,2 – минимальная толщина плиты под стаканом; 0,15 – расстояние от обреза фундамента до пола первого этажа. При этом минимальную высоту фундамента желательно назначать кратной 300 мм. Размеры подошвы фундамента l × b при относительном эксцентриситете продольной силы e = l/10 назначают из условия (7.1), принимая pmax = 1,2R0,pmin = 0,25 pmax, A= N 0,75R0 − γ mt d A= ; N 0,6 R0 − γ mt d = 1,05 . A(7.3) при относительном эксцентриситете продольной силы e = l/6 размеры подошвы назначают из условия (7.1), принимая pmax = 1,2R0, pmin = 0, A= N 0,75R0 − γ mt d A= ; N 0,6 R0 − γ mt d . A = 1,05 N R0 − γ mt d , l= N 0,75R0 − γ mt d ; A= N 0,6 R0 − γ mt d . A = 1,05 N R0 − γ mt d , l= А 0,8 где R0 – расчетное сопротивление грунта, фиксированное для фундаментов шириной 1 м на глубине 2 м, принимаемое по результатам инженерно-геологических изысканий площадки строительства и по указаниям норм. Далее задаются соотношением размеров подошвы фундамента b/l = 0,8 и вычисляют ее размеры A= N 0,6 R0 − γ mt d . A = 1,05 N R0 − γ mt d , l= А 0,8 ; b = 0,8 l. – 116 – R0 − γ mt d А 0,8 При незначительном эксцентриситете продольной силы размеры подошвы можно назначать из условия A= N (7.4) , Полученные значения размеров подошвы фундамента округляют до стандартных размеров, кратных 300 или 100 мм. Окончательные размеры подошвы фундамента принимают после проверки несущей способности основания. Расчетное сопротивление грунта R вычисляют после определения размеров подошвы фундамента. 7.3. Проверка несущей способности фундамента Проверка несущей способности оснований производится по уточненным размерам фундамента и нормативным усилиям на уровне подошвы фундамента. Продольная сила на уровне подошвы фундамента Ninf = N + Adγmt, (7.5) где N – значение продольного усилия в колонне на уровне верхнего обреза фундамента с коэффициентом надежности по нагрузке γf = 1,0. Для фундаментов крайних рядов колонн к нему необходимо добавлять нормативное значение усилий, передаваемое с фундаментных балок и опирающихся на них стеновых панелей с коэффициентом надежности по нагрузке γf = 1,0; d – глубина заложения фундамента, d = h + 0,15 м; γm – средний объемный вес фундамента и грунта на его уступах, принимаемый равным 20 кН/м3. Изгибающий момент на уровне подошвы фундамента Minf = Mn + Qn h, (7.6) где Mn – значение изгибающего момента в колонне на уровне верхнего обреза фундамента с коэффициентом надежности по нагрузке γf = 1,0. Для фундаментов крайних рядов колонн к нему необходимо добавлять значение изгибающего момента от усилий, передаваемых с фундаментных балок с эксцентриситетом eф.б, равное Mф.б = Nф.б eф.б. Значение эксцентриситета eф.б определяется из условия опирания фундаментной балки на фундамент. Расчетное сопротивление грунта на глубине d при конкретной ширине фундамента b: при d ≤ 2 м R = R0 [I + k1(b – b0)/b0](d + d0)/2d0; – 117 – (7.7) при d > 2 м R = R0 [I + k1(b – b0)/b0] + γ k2(d – d0), (7.8) где R0 – расчетное давление грунта, фиксированное для фундаментов шириной 1 м на глубине 2 м, принимаемое по результатам инженерно-геологических изысканий площадки строительства и по указаниям норм; b и d – соответственно ширина и глубина заложения проектируемого фундамента, м; b0 = 1 м; d0 = 2 м; γ – нагрузка от 1 м3 грунта, расположенного выше подошвы фундамента, кН/м3; k1 = 0,125 – коэффициент, принимаемый для оснований, сложенных крупнообломочными и песчаными грунтами; k1 = 0,05 – то же, пылеватыми песками, супесями, суглинками и глинами; k2 = 0,25 – коэффициент, принимаемый для оснований, сложенных крупнообломочными и песчаными грунтами; k2 = 0,2 – то же, супесями и суглинками; k2 = 1,15 – то же, глинами. Напряжения под подошвой фундамента исчисляют по формуле N inf 6e M inf N M . pmax (7.9) = + 1 ± , e = A l N inf A W N inf 6e M inf N M = ± 1 , e = . p = + где max A l N inf A W При этом должны соблюдаться условия pmax ≤ 1,2R и pmin ≥ 0. Если условия выполняются, то размеры подошвы фундамента оставляют без изменения, если нет, то размеры подошвы фундамента увеличивают. Недопустим также большой запас несущей способности. Расчет на продавливание плитной части внецентренно нагруженных железобетонных фундаментов производится из условия прочности только одной наиболее нагруженной грани пирамиды продавливания по усилиям от расчетных нагрузок при γf ≥ 1 из условия p= F ≤ Rbt bm ho,pl, (7.10) где F – величина продавливающей силы, принимаемая равной F = A0 pmax, здесь А0 – часть площади основания фундамента, ограниченная нижним основанием рассматриваемой грани пирамиды продавливания и продолжением в плане соответствующих ребер, A0 = 0,5b(l – hсf – 2h0,pl) – 0,25(b – bсf – 2h0,pl)2, (7.11) при b – bсf – 2h0,pl ≤ 0 последний член в формуле не учитывается; bсf,hсf – ширина и высота сечения подколонника соответственно; – 118 – pmax – максимальное краевое давление на грунт от расчетной нагрузки с коэффициентом надежности по нагрузке γf = 1,0, приложенной на уровне верхнего обреза фундамента (без учета веса фундамента и грунта на его уступах), определяемое по формуле p= N inf 6e M inf N M (7.12) . pmax = + , 1 ± , e = A l N inf A W bm – средний размер проверяемой грани вычисляется по формулам: при b – bсf > 2h0,pl bm = bcf + h0,pl; (7.13) при b – bсf ≤ 2h0,pl bm = 0,5(b + bcf), где h0,pl – рабочая высота плиты (7.14) h0,pl = hpl – a, где a – расстояние от низа подошвы плиты до центра арматуры фундамента, принимаемое равным 50…80 мм в зависимости от наличия или отсутствия подготовки. 7.4. Определение сечений арматуры плитной части фундамента Плита фундамента под действием реактивного давления грунта снизу работает на изгиб. Армирование фундамента по подошве определяют расчетом на изгиб по нормальным сечениям, проходящим по боковым граням ступеней и подколонника. Изгибающие моменты в i-м сечении на расстоянии сi от наиболее нагруженного края фундамента на всю ширину фундамента при трапециевидной и треугольной эпюрах давления грунта (е ≤ l/6) в направлении действия момента Мх вычисляют по формуле Mi = Nci2(1 + 6ex /l – 4exci /l2)/2l. (7.15) Площадь арматуры определяют в следующей последовательности. Вычисляют коэффициент αm αm = M xi Rb γ b1bi h02,i – 119 – , ( ) As = Rb bh0 1 − 1 − α(7.16) m / Rs . где bi – ширина сжатой зоны (в верхней части) рассматриваемого сечения; h0i – рабочая высота рассматриваемого сечения; γb1 = 0,9 – коэффициент условий работы для бетонных и железобетонных конструкций при действии только постоянных и длительных нагрузок, вводимый к расчетным сопротивлениям Rb и Rbt. Требуемую площадь сечения растянутой арматуры находим по формуле M xi As = Rb bh0 1 − 1 − α m / Rs . , αm = (7.17) Rb γ b1bi h02,i Примеры армирования подошвы фундамента приведены на рис. 7.2. В случае когда меньшая из сторон подошвы фундамента имеет размер b ≤ 3 м, следует применять сетки с рабочей арматурой в двух направлениях (рис. 7.2, а). При b > 3 м применяются отдельные сетки с рабочей арматурой в одном направлении, укладываемые в двух плоскостях. При этом рабочая арматура, параллельная большей стороне подошвы l, укладывается снизу. Сетки в каждой из плоскостей укладываются без нахлестки с расстоянием между ними не более 200 мм (рис. 7.2, б). При больших размерах подошвы фундамента b > 3 м экономичнее применять вязаные сетки, в которых отсутствует монтажная арматура. Минимальный диаметр рабочей арматуры сеток подошвы принимается равным 10 мм вдоль стороны l ≤ 3 м и 12 мм при l > 3 м. Железобетонные подколонники армируют вертикальными сварными плоскими сетками, объединяемыми в пространственный каркас. Сетки рекомендуется ставить по четырем сторонам подколонника (рис. 7.3). При расчетном или конструктивном армировании подколонника диаметр продольных стержней вертикальной арматуры принимается не менее 12 мм. Горизонтальное армирование стаканной части подколонника осуществляется сварными плоскими сетками с расположением продольных стержней у наружных и внутренних поверхностей стенок стакана. Продольная вертикальная арматура должна размещаться внутри горизонтальных сеток. Диаметр стержней сеток принимается не менее 8 мм и не менее четверти диаметра продольной арматуры вертикального армирования подколонника. ( – 120 – ) 200 600 l 2 200 1 600 1 200 1 200 b <(=)3000 b >3000 1-1 l cf l cf 1 h pl h o,pl 2 f Lc 1 б) 0 5 0 5 а) f c b Рис. 7.2. Армирование подошвы фундамента: а – при b ≤ 3 м; б – при b > 3 м; 1 – нижние сетки; 2 – верхние сетки 5 2 p 1 d 1 f dc df f Lc 0 5 0 5 c b f 5 2 1 Рис. 7.3. Армирование5 железобетонного подколонника 2 пространственными каркасами, собираемыми из плоских сеток: p d 1 – арматурная сетка f dc df – 121 – Расположение сеток следует принимать по рис. 7.4. В пределах высоты стакана стенки армируют горизонтальными сетками в количестве пяти штук при глубине 700 мм и шести при большей глубине. Толщина защитного слоя бетона для рабочей арматуры подколонника должна быть не менее 30 мм, а для подошвы фундамента при условии устройства под ним бетонной подготовки принимается равной 35 мм. 0 5 0 5 1 1 f Lc f bc б) 1 1 0 50 0 5 0 1 г а ш 0 0 2 г а 5 ш 0 2 0 1 n х 0 0 1 1 1 а) 0 5 2 1 . . . 0 5 4 = p d 0 5 0 0 0 5 0 5 2 1 . . . г а 0 5 ш 0 0 4 2 г = а р ш d 5 0 2 0 1 n х 0 0 1 Рис. 7.4. Схема расположения горизонтальных сеток армирования подколонника: а – при еа > lc/2; б – при lc/6 < еа ≤ lc/2 Расчет подколонника в сечениях по стакану производят как внецентренно нагруженного элемента с расчетным двутавровым сечением без учета ηv, ηh и еа на продольную силу (N–Nc) и изгибающего момента в уровне заделанного конца колонны. Расчетное усилие Nc определяют по формуле Nc = αN, (7.18) где N – расчетное продольное усилие, передаваемое с колонны на фундамент; Nc – продольное усилие, передаваемое с колонны на плитную часть фундамента; α – коэффициент, учитывающий час- – 122 – тичную передачу продольной силы N на плитную часть фундамента через стенки стакана и принимаемый равным α = (1 – 0,4RbtAc/N), но не менее 0,85, (7.19) где Ac = 2(bc + hc)dc – площадь боковой поверхности колонны, заделанной в фундамент; Rbt – расчетное сопротивление бетона замоноличивания стакана с учетом коэффициентов условий работы γb1, γb2 по табл. 5.2 СП 52-101–2003. Для увеличения несущей способности подколонника по смятию бетона под торцом колонны ниже стакана устанавливают две горизонтальные сетки косвенного армирования (рис. 7.4, б). Бетонные столбики для опирания фундаментных балок, как правило, бетонируют после изготовления фундаментов, но могут бетонировать и одновременно. 7.5. Пример расчета фундамента Дано: продольная сила в колонне на уровне верхнего обреза фундамента N = 1532,96 кН; изгибающий момент М = 50,97 кН·м (из расчета колонны); поперечная сила определена по изгибающим моментам в колонне Q = –(MB + MH)/l = –(101,94 + 50,97)/6 = –25,5 кН; грунт – супесь, коэффициент пористости е = 0,7, IL = 0, R0 = 250 кПа; глубина промерзания – 1,6 м. Бетон фундамента В15, Rb = 8,5 МПа, Rbt = 0,75 МПа. Арматура плитной части фундамента класса А300 с Rs = 270 МПа. Принимаем типовой размер подколонника: сечение подколонника lcf × bcf = 900×900 мм; глубина стакана dp = 800 мм, размер стакана понизу – 500×500 мм, поверху – 550×550 мм. Определение размеров подошвы и глубины заложения фундамента Глубина заложения фундамента из условия промерзания грунта d = 1,75 м. Высота фундамента h = 1,75 – 0,15 = 1,60 м. Нормативные нагрузки на фундамент: Nn = 1532,96/1,15 = 1333,0 кН, Mn = 50,97/1,15 = 44,32 кН·м, Qn = –25,5/1,15 = –22,17 кН. Предварительно размер подошвы фундамента определяем из предположения, что относительный эксцентриситет равен e = l/10 – 123 – A= N 0,75R0 − γ mt d = 1333 = 8,68 м 2 . l = А 0,8 = 8,68 / 0,8 = 3,2 0,75 ⋅ 250 − 20 ⋅1,75 Далее задаемся соотношением размеров подошвы фундамента b/l = 0,8 и вычисляем ее размеры: 3 = 8,68 м 2 20 ⋅1,75 l = А 0,8 = 8,68 / 0,8 = 3,294 м; b = 0,8 l = 0,8 · 3,294 = 2,63 м. Назначаем размеры подошвы фундамента l×b = 3,3×2,7 м, А = 8,91 м2. Проверка несущей способности оснований Расчетное сопротивление грунта на глубине d при конкретной ширине фундамента b = 2,7 м, при d = 1,75 м R = R0[1 + k1(b – b0)/b0](d + d0)/2d0 = = 250[1 + 0,05(2,7 – 1,0)/1,0](1,75 + 2,0)/2 · 2 = 251 кПа. Продольная сила на уровне подошвы фундамента: Ninf = Nn + Adγmt = 1333 + 8,91 · 1,75 · 20 = 1635,94 кН. Изгибающий момент на уровне подошвы фундамента. Поперечная сила имеет знак, противоположный изгибающему моменту: Minf = Mn – Qn h = 44,32 – 22,17 · 1,6 = 6,63 кН·м. Напряжения под подошвой фундамента pmax и pmin: N inf N6e 1635 6 ⋅ 0,0041 ,94 ,94 = 184 ,=98 < ,198 ,2 R кПа;кПа; 1 + 1 + 6 ⋅ 0,0041 1=+ inf=1 + 6e = 1635 184 < 1=,2298 R = 298 pmax A lA 8l ,91 8,91 3,3 3,3 pmax = pmin = N inf N6infe 1635 6 ⋅0,0041 6 ⋅ 0,0041 6e ,941635 ,94 182кПа, ,24 кПа, pmin1=− 1=− = 1 − 1 − =,24 = 182 Al l8,91 A 8,91 3,3 3,3 6,63 inf M inf e = 6M,63 = 0,0041 м. Фундамент практически центрально e = где = N = =1635 0,0041 ,94 N inf 1635inf,94 нагружен. Размеры фундамента получились несколько завышенными. Принимаем размеры фундамента l × b = 3,0×2,4 м, А = 7,2 м2. Уточняем расчетное сопротивление грунта при ширине фундамента b = 2,4 м; R = 251 кПа. Вычисляем максимальное давление под подошвой фундамента: pmax = p min = N inf 6e 1635,94 6 ⋅ 0,0041 1 + = 229 кПа < 1,2 ⋅ 251 = 296,4 кПа. 1 + = A l 3,0 7,2 N inf A 0,0041 124–= 225 6e 1635,94 6 ⋅ – 1 − 1 − = l 7, 2 3,0 pmax = N inf A 6e 1635,94 6 ⋅ 0,0041 1 + = 229 кПа < 1,2 ⋅ 251 = 296,4 кПа. 1 + = l 3,0 7,2 Минимальное давление под подошвой фундамента: p min = N inf 6e 1635,94 6 ⋅ 0,0041 1 − = 225 кПа. 1 − = A l 7, 2 3,0 Среднее давление под подошвой фундамента: p max = N M 1532,96 6 ⋅ 50,97 + ==(229 + 225)/2 + = 227 2 кПа. m A pW 7, 2 2,4 ⋅ = 3,0227 Принимаем двухступенчатую подошву фундамента общей высотой hpl = 0,6 м (рис. 7.5). Размеры второй ступени l1 × b1 = 2,1×1,8 м. Рис. 7.5. Конструкция фундамента Расчет на продавливание плитной части Расчет на продавливание плитной части внецентренно нагруженного фундамента производят из условия прочности только одной наиболее нагруженной грани пирамиды продавливания по усилиям от расчетных нагрузок при γf > 1. Определяем максимальное краевое давление на грунт от расчетной нагрузки с коэффи- – 125 – pmax = N inf 6e 1635,94 6 ⋅ 0,0041 1 + = 229 кПа < 1,2 ⋅ 251 = 29 1 + = 3,0 7,2 A l циентом надежности γf >,94 1,0, на уровне N по 6e 1635 6 ⋅ 0,0041 приложенной нагрузке p min = inf 1 − = 1 − = 225 верхнего обреза фундамента и грунта A l (без 7учета ,2 веса фундамента 3,0 на его уступах): N M 1532,96 6 ⋅ 50,97 p max = + = + = 227 кПа. A W 7, 2 2,4 ⋅ 3,0 2 Продавливающая сила F = A0 pmax = 1,2 · 229 = 275 кН, где A0 = 0,5b(l – hcf – 2h0,pl) – 0,25(b – bсf – 2h0,pl)2 = = 0,5 · 2,4(3,0 – 0,9 – 2 · 0,53) – 0,25(2,4 – 0,9 – 2 · 0,53)2 = 1,2 м. Рабочая высота подошвы фундамента h0,pi = h – a = 0,6 – 0,07 = 0,53 м. Проверяем прочность наиболее нагруженной грани на продавливание: F = 275 < Rbt bm ho,pl = 0,75 · 1430 · 530 = 568425 Н = 568,425 кН, где bm = bcf + h0,pl = 0,9 + 0,53 = 1,43 м. Прочность наиболее нагруженной грани на продавливание обеспечена. Определение сечений арматуры плитной части фундамента Армирование фундамента по подошве определяют расчетом на изгиб по нормальным сечениям, проходящим по боковым граням ступеней и подколонника. Вычисляют изгибающий момент в сечении 1-1 на расстоянии с1 = 0,45 м от наиболее нагруженного края фундамента на всю ширину фундамента и в сечении 2-2 на расстоянии с2 = 1,05 м (рис. 7.5), е = M/N = 50,97/1532,96 = 0,033 м. M 1 = Nc12 (1 + 6e / l − 4ec1 / l 2 ) / 2l = 1532,96 ⋅ 0,452 (1 + 6 ⋅ 0,033 / 3,0 − 4 ⋅ 0,033 ⋅ 0,45 / 3,02 ) / 2 ⋅ 3,0 = 54,81 кНм; M 2 = Nc22 (1 + 6e / l − 4ec2 / l 2 ) / 2l = 1532,96 ⋅ 1,052 (1 + 6 ⋅ 0,033 / 3,0 − 4 ⋅ 0,033 ⋅ 1,05 / 3,02 ) / 2 ⋅ 3,0 = 295,93 кНм. – 126 – Подбор арматуры: − сечение 1 h0,1 = h1 − a = 300 − 70 = 230 мм; M1 54,81 ⋅ 10 6 = 0,05; = 2 Rb bh0,1 8,5 ⋅ 2400 ⋅ 230 2 αm = ξ = 1 − 1 − 2α m = 1 − 1 − 2 ⋅ 0,05 = 0,052; As1 = Rb bh0,1ξ = Rs 8,5 ⋅ 2400 ⋅ 230 ⋅ 0,052 = 906 мм 2; 270 − сечение 2 h0, 2 = h2 − a = 600 − 70 = 530 мм; αm = M2 Rb b1h02,2 = 295,93 ⋅106 = 0,069; 8,5 ⋅1800 ⋅ 5302 ξ = 1 − 1 − 2α m = 1 − 1 − 2 ⋅ 0,069 = 0,0716; As 2 = Rb bh0,2 ξ Rs = 8,5 ⋅1800 ⋅ 530 ⋅ 0,0716 = 2149,2 мм 2. 270 Принимаем 12 D 16 A300 c As = 2412 мм2. В перпендикулярном направлении плита фундамента работает как центрально нагруженная со средним давлением рm = 1532,96/7,2 = 212,9 кПа. Изгибающие моменты в сечениях 3−3 и 4−4: M 3 = 0,125 p m l (b − b1 )22 = 0,125 ⋅ 212,9 ⋅ 3,0( 2,4 − 1,8)22 = 51,1 M 3 = 0,125 p m l (b − b1 ) = 0,125 ⋅ 212,9 ⋅ 3,0( 2,4 − 1,8) = 51,1 кН·м; M 4 = 0,125 pm l (b − bcf )22 = 0,125 ⋅ 212,9 ⋅ 3,0(2,4 − 0,9)22 = 179,63 кН·м. M 4 = 0,125 pm l (b − bcf ) = 0,125 ⋅ 212,9 ⋅ 3,0(2,4 − 0,9) = 179,63 Подбор арматуры выполняют по моменту в сечениях 3−3 и 4−4: αm = M3 Rb bh02,1 = 51,1 ⋅10 6 = 0,0379; 8,5 ⋅ 3000 ⋅ 230 2 ξ = 1 − 1 − 2α m = 1 − 1 − 2 ⋅ 0,0379 = 0,0386; As 3 = Rb bh0,1ξ Rs αm = = 8,5 ⋅ 3000 ⋅ 230 ⋅ 0,0386 = 839,5 мм 2; 270 M4 179,63 ⋅ 10 6 = = 0,0358; Rb bh02, 2 8,5 ⋅ 2100 ⋅ 530 2 – 127 – ξ =1− 1 − 2 αm = 1 − 1 − 2 ⋅ 0 , 0358 = 0 , 0365 ; 88,,55⋅⋅3000 3000⋅⋅230 230⋅⋅00,,0386 0386 AAss33 == bb 00,1,1 == == 839 839,,55 мм мм22;; R R 270 270 R bh ξ 8,5 ⋅ 3000 ⋅ 230 ⋅ss0,0386 As 3 = b 0,1 = = 839,5 мм 2; Rs 270 M M44 179 179,,63 63⋅⋅10 1066 ααmm == = = == 00,,0358 0358;; bh0202,,22 88,,55⋅⋅2100 2100⋅⋅530 53022 M4 179,63 ⋅ 10RR6bbbh αm = = = 0,0358; 2 Rb bh02, 2 8ξξ,5==⋅ 12100 ⋅ 530 1 −− 11 −− 22α α == 11 −− 11 −− 22 ⋅⋅ 00,,0358 0358 == 00,,0365 0365 ;; m m ξ =1− As 4 1 − 2 αm = 1 − 1RR−bh 2 ⋅ 0ξξ, 0358 0 , 0365 bh 88,,55⋅⋅=2100 2100 ⋅⋅530 530; ⋅⋅00,,0365 0365 AAss44 == bb 00,,22 == ==1278 1278,,99 мм мм22.. R R 270 270 R bh ξ 8,5 ⋅ 2100 ⋅ 530 ⋅ss0,0365 = b 0, 2 = = 1278,9 мм 2 . Rs 270 Принимаем 15 D12 A300 c As = 1696 мм2. Подошву армируем вя85 85 16 16АА300 300 −− 200 200 заной сеткой 2370 2970 2970××2570 2570 . 85 85 12 12АА300 300 200 85 −− 200 16 А300 − 200 2970 × 2570 85 12 А300 − 200 – 128 – Библиографический список 1. Свод правил СП 20.13330.2011. Нагрузки и воздействия. Актуализированная редакция СНиП 2.01.07–85*. Свод правил нагрузки и воздействия. Минрегион России. – М. : ОАО «ЦПП», 2011. – 80 с. 2. Свод правил СП 63.13330.2012. Бетонные и железобетонные конструкции. Основные положения. Актуализированная редакция СНиП 52-01–2003. Минрегион России. – М. : ОАО «ЦПП», 2012. – 161 с. 3. ГОСТ Р 54257–2010. Надежность строительных конструкций и оснований. Основные положения и требования. Минрегион России. – М. : ОАО «ЦПП», 2011. – 29 с. 4. ГОСТ 21.503–80. Система проектной документации для строительства. Конструкции бетонные и железобетонные. Рабочие чертежи. – М. : Изд-во стандартов, 1981. – 18 с. 5. Свод правил СП 52-101–2003. Бетонные и железобетонные конструкции без предварительного напряжения арматуры. – М. : ФГУП ЦПП, 2004. – 54 с. 6. Свод правил СП 52-102–2004. Предварительно напряженные железобетонные конструкции. – М. : ФГУП ЦПП, 2004. – 36 с. 7. Пособие по проектированию бетонных и железобетонных конструкций из тяжелого бетона без предварительного напряжения арматуры (к СП 52-101–2003). – М. : ОАО ЦНИИПромзданий, 2005. – 212 с. 8. Пособие по проектированию предварительно напряженных железобетонных конструкций из тяжелого бетона (к СП 52-102– 2004). – М. : ОАО ЦНИИПромзданий, 2005. – 157 с. 9. Свод правил СП 22.13330.2011. Основания зданий и сооружений. Актуализированная редакция СНиП 2.02.01–83* Минрегион России. – М. : ОАО «ЦПП», 2012. – 48 с. 10. Свод правил СП 50-101–2004. Проектирование и устройство оснований и фундаментов зданий и сооружений. – М. : ФГУП ЦПП, 2004. – 130 с. 11. Пособие по проектированию фундаментов на естественном основании под колонны зданий и сооружений (к СНиП 2.03.01–84 и СНиП 2.02.01–83). – М. : ЦИТП Госстроя СССР, 1987. – 112 с. – 129 – 12. Типовые железобетонные конструкции зданий и сооружений для промышленного строительства / В.М. Спиридонов [и др.] ; под общ. ред. Г.И. Бердичевского. – 2-е изд., перераб. и доп. – М. : Стройиздат, 1981. – 488 с. – (Справочник проектировщика). 13. Ильяшев, А.С. Пособие по проектированию промышленных зданий : учеб. пособие для вузов по спец. «Промышленное и гражданское строительство»/А.С. Ильяшев, Ю.С. Тимянский, Ю.Н. Хромец ; под ред. Ю.Н. Хромца. – М. : Высш. шк., 1990. – 304 с. 14. Филиппов, В.А. Проектирование конструкций железобетонных одноэтажных производственных зданий : учеб. пособие / В.А. Филиппов. – Тольятти : ТГУ, 2007. – 193 с. – 130 – Приложение Таблица П1 Нормативные сопротивления бетона Нормативные сопротивления бетона R и Rbt,n и расчетные Вид со- сопротивления для предельных состоянийb,nвторой группы Rb,ser и против- R , МПа (кгс/см2), при классе бетона по прочности на сжатие bt,ser ления В10 В15 В20 В25 В30 В35 В40 В45 В50 В55 В60 Сжатие 7,5 11,0 15,0 18,5 22,0 25,5 29,0 32,0 36,0 39,5 43,0 осевое (8,7) (112) (153) (188) (224) (260) (296) 326 (367) (403) (438) Rbn, Rb,ser Растяже0,85 1,10 1,35 1,55 1,75 1,95 2,10 2,25 2,45 2,60 275 ние (8,7) (11,2) (13,8) (15,8) (17,8) (19,9) (21,4) (22,9) (25,0) (26,5) (28,0) Rbt,n Rbt,ser Таблица П2 Расчетные сопротивления бетона Вид сопротивления Расчетные сопротивления бетона для предельных состояний первой группы Rb и Rbt, МПа (кгс/см2), при классе бетона по прочности на сжатие В10 В15 В20 В25 В30 В35 В40 В45 В50 В55 В60 Сжатие 6,0 8,5 11,5 14,5 17,0 19,5 22,0 25 27,5 30,0 33,0 осевое (61,2) (86,5) (117) (148) (173) (199) (224) (255) (280) (306) (336) Rb Растяже0,56 0,75 0,90 1,05 1,15 1,30 1,40 1,50 1,60 1,70 1,8 ние (5,7) (7,6) (9,2) (10,7) (11,7) (13,3) (14,3) (15,3) (16,3) (17,3) (18,3) Rbt Таблица П3 Начальный модуль упругости бетона при сжатии и растяжении Значения начального модуля упругости бетона при сжатии и растяжении Eb⋅10-3, МПа (кгс/см2), при классе бетона по прочности на сжатие В10 В15 В20 В25 В30 В35 В55 В60 19,0 24 27 30 32,5 34,5 36 37 8,0 39,0 (194) (245) (280) (306) (331) (352) (367) (377) (387) (398) 39,5 (403) – 131 – В40 В45 В50 Таблица П4 Значение коэффициента φb,cr Значение коэффициента ползучести φb,cr Относительная при классе бетона на сжатие влажность воздуха окружающей В15 В20 В25 В30 В35 В40 В45 В50 В55 В60 среды, % выше 75 (повышенная) 2,4 2,0 1,8 1,6 1,5 1,4 1,3 1,2 1,1 1,0 40–75 (нормальная) 3,4 2,8 2,5 2,3 2,1 1,9 1,8 1,6 1,5 1,4 ниже 40 (пониженная) 4,8 4,0 3,6 3,2 3,0 2,8 2,6 2,4 2,2 2,0 Примечание. Относительную влажность воздуха окружающей среды принимают по СНиП 23-01–99 как среднюю месячную относительную влажность наиболее теплого месяца для района строительства. Таблица П5 Нормативные сопротивления стержневой арматуры A240 6–40 Нормативные значения сопротивления растяжению Rs,n и расчетные значения сопротивления растяжению для предельных состояний второй группы Rs,ser, МПа (кгс/см2) 240 (2450) A300 10–40 300 (3050) A400 6–40 400 (4050) A500 6–40 500 (5100) A540 20–40 540 (5500) A600 10–40 600 (6100) Арматура классов Номинальный диаметр арматуры, мм A800 10–40 800 (8150) А1000 10–40 1000 (1020) В500 3–12 500 (5100) Вр1200 8 1200(12200) Вр1300 7 1300 (13200) Вр1400 4; 5; 6 1400 (14300) Вр1500 3 1500 (15300) К1400(К-7) 15 1400 (14300) К1500(К-7) 6; 9; 12 1500 (15300) К1500(К-19) 14 1500 (15300) – 132 – Таблица П6 Расчетные сопротивления арматуры Расчетные значения Расчетные значения сосопротивления арматуры противления арматуры для предельных состодля предельных состояАрматура ний первой группы, МПа Арматура яний первой группы, классов классов МПа (кгс/см2) (кгс/см2) растяжению Rs сжатию Rsc A240 215 (2200) 215 (2200) В500 A300 270 (2750) 270 (2750) Вр1200 1000 (10200) 400 (4100) A400 355 (3600) 355 (3600) Вр1300 1070 (10900) 400 (4100) A500 435 (4450) 400 (4100) Вр1400 1170 (11900) 400 (4100) A540 450 (4600)* 200 (2000) Вр1500 1250 (12750) 400 (4100) A600 A800 520 (5300) 695 (7050) 400 (4100) 400 (4100) К1400 К1500 1170 (11900) 400 (4100) 1250 (12750) 400 (4100) А1000 830 (8450) 400 (4100) растяжению Rs сжатию Rsc 415 (4250) 360 (3650) * Если при упрочнении вытяжкой арматуры класса А540 контролируется удлинение и напряжение арматуры, расчетное сопротивление растяжению Rs допускается принимать равным 490 МПа (5000 кгс/см2). Таблица П7 Модуль упругости арматуры Класс арматуры Модуль упругости арматуры ES, МПа (кгс/см2) Класс арматуры Модуль упругости арматуры ES·10-4, МПа (кгс/см2) A240…А1000 2·105 (2·106) Bр1200…Bр1500 2·105 (2·106) В500 2·105 (2·106) К1400, K1500 18·105(1,8·106) Таблица П8 Расчетное сопротивление растяжению поперечной арматуры Класс арматуры Расчетное сопротивление поперечной арматуры Rsw, МПа (кгс/см2) А240 А300 А400 А500 В500 170 (1730) 215 (2190) 285 (2900) 300 (3060) 300 (3060) – 133 – Таблица П9 Значения ξR и αR Класс арматуры Значение ξR А240 А300 А400 А500 В500 0,612 0,577 0,531 0,493 0,502 Значение αR 0,425 0,411 0,390 0,372 0,376 Таблица П10 Значение ξR в предварительно напряженной арматуре ssp /Rs 1,2 1,1 1,0 0,99 0,8 0,7 0,6 0,5 Значение ξR при растянутой арматуре классов А540 А600 А800 А1000 Вр1200 Вр1300 Вр1400 Вр1500 К1400 К1500 0,93 0,86 0,80 0,75 0,70 0,66 0,62 0,59 0,56 0,53 0,51 0,49 0,47 0,45 0,43 0,41 0,58 0,54 0,51 0,48 0,45 0,43 0,41 0,39 0,60 0,55 0,51 0,47 0,44 0,42 0,39 0,37 0,62 0,56 0,51 0,47 0,43 0,40 0,37 0,35 0,63 0,53 0,51 0,46 0,43 0,39 0,37 0,34 0,65 0,57 0,51 0,46 0,42 0,39 0,36 0,33 0,66 0,57 0,51 0,46 0,41 0,38 0,35 0,32 0,63 0,55 0,49 0,44 0,40 0,36 0,34 0,31 0,65 0,56 0,49 0,44 0,39 0,36 0,33 0,30 Таблица П11 Значение коэффициента γ при различных формах поперечного сечения элемента Коэффициент γ 1. Тавровое с полкой, расположен1,3 ной в сжатой зоне Сечение 2. Двутавровое симметричное (коробчатое): а) при b′f /b = bf/b ≤ 2 б) при 2 < b′f /b = bf/b ≤ 6 в) при b′f /b = bf /b > 6 1,35 1,25 1,20 – 134 – Форма поперечного сечения Коэффициент γ Сечение 3. Двутавровое несимметричное, удовлетворяющее условию b′f /b ≤ 3: а) при bf /b ≤ 2 б) при 2 < bf /b ≤ 6 в) при bf /b > 6 Форма поперечного сечения 1,20 1,15 1,10 4. Двутавровое несимметричное, удовлетворяющее условию b′f /b < 3: а) при bf /b ≤ 4 независимо от отношения hf /h б) при bf /b > 4 и hf /h ≥ 0,2 в) при bf /b > 4 и hf /h < 0,2 1,25 5. Двутавровое несимметричное, удовлетворяющее условию b′f /b ≥ 8: а) при hf /h > 0,3 б) при hf /h ≤ 0,3 1,50 1,25 1,20 1,25 Примечание. Обозначения bf и hf соответствуют размерам полки, которая при расчете по образованию трещин является растянутой, а b′f и h′f – размерам полки, которая для этого случая расчета является сжатой. Таблица П12 Значение коэффициента ζ φf es /h0 0,7 0,8 0,9 0,0 1,0 1,1 ≥1,2 0,7 0,8 0,2 0,9 1,0 ≥1,2 Коэффициенты ζ = z/h0 при значениях µαsl, равных 0,02 0,70 0,77 0,82 0,84 0,85 0,85 0,70 0,79 0,85 0,87 0,88 0,03 0,69 0,76 0,80 0,82 0,83 0,83 0,70 0,79 0,84 0,86 0,87 0,05 0,69 0,74 0,77 0,78 0,79 0,79 0,70 0,78 0,82 0,84 0,85 0,07 0,69 0,73 0,76 0,77 0,77 0,77 0,70 0,77 0,81 0,83 0,83 0,10 0,68 0,72 0,74 0,74 0,74 0,74 0,70 0,77 0,80 0,81 0,81 0,15 0,68 0,70 0,71 0,71 0,71 0,70 0,70 0,76 0,78 0,79 0,79 – 135 – 0,20 0,68 0,69 0,70 0,69 0,68 0,67 0,70 0,75 0,77 0,77 0,77 0,25 0,30 0,40 0,50 0,67 0,67 0,67 0,67 0,68 0,68 0,67 0,66 0,68 0,67 0,66 0,64 0,67 0,66 0,64 0,62 0,66 0,65 0,62 0,60 0,65 0,63 0,60 0,58 0,70 0,70 0,70 0,70 0,75 0,74 0,74 0,73 0,76 0,75 0,74 0,73 0,76 0,75 0,74 0,72 0,75 0,74 0,72 0,70 φf es /h0 0,7 0,8 0,4 0,9 1,0 ≥1,2 0,8 0,9 0,6 1,0 ≥1,2 0,8 0,9 0,8 1,0 ≥1,2 Коэффициенты ζ = z/h0 при значениях µαsl, равных 0,02 0,03 0,05 0,07 0,10 0,15 0,20 0,25 0,70 0,80 0,87 0,89 0,88 0,80 0,87 0,89 0,90 0,80 0,89 0,89 0,90 0,70 0,70 0,70 0,70 0,79 0,77 0,77 0,77 0,80 0,79 0,78 0,77 0,80 0,79 0,78 0,77 0,80 0,79 0,77 0,76 0,79 0,79 0,79 0,79 0,82 0,81 0,80 0,80 0,83 0,82 0,81 0,80 0,82 0,81 0,80 0,79 0,80 0,80 0,80 0,80 0,83 0,83 0,82 0,82 0,84 0,83 0,83 0,82 0,84 0,83 0,82 0,81 ϕf = 0,70 0,79 0,86 0,88 0,87 0,80 0,87 0,88 0,88 0,80 0,87 0,89 0,88 0,70 0,79 0,84 0,86 0,86 0,80 0,86 0,87 0,87 0,80 0,86 0,88 0,87 0,70 0,79 0,83 0,85 0,85 0,80 0,85 0,87 0,86 0,80 0,86 0,87 0,87 0,70 0,79 0,82 0,84 0,84 0,80 0,84 086 0,85 0,80 0,85 0,87 0,86 (b′f − b) h′f + α s1 Asp′ + α s 2 As′ ; bh0 0,70 0,78 0,81 0,82 0,8 0,79 0,83 0,84 0,84 0,80 0,84 0,86 0,85 es = 0,70 0,78 0,80 0,81 0,81 0,79 0,82 0,83 0,83 0,80 0,84 0,85 0,84 0,30 0,40 0,50 α s1 Asp + α s1 As Ms . ; μα s1 = bh0 P Таблица П13 Значения коэффициента φс φf es /ho 0,0 0,2 0,4 0,7 Коэффициент φс при значениях μas2, равных 0,03 0,05 0,07 0,10 0,15 0,20 0,25 0,30 0,40 0,50 0,60 0,70 0,90 1,10 1,50 2,00 0,29 0,29 0,30 0,30 0,30 0,31 0,31 0,31 0,32 0,32 0,32 0,32 0,32 0,33 0,33 0,33 0,8 0,18 0,20 0,21 0,22 0,24 0,25 0,26 0,27 0,28 0,28 0,29 0,29 0,30 0,31 031 0,32 0,9 0,12 0,14 0,16 0,18 0,20 0,21 0,23 0,24 0,25 0,26 0,27 0,27 0,28 0,29 0,30 0,31 1,0 0,09 0,11 0,1З 0,15 0,18 0,19 0,20 0,21 0,23 0,24 0,25 0,26 0,27 0,28 0,29 0,30 1,1 0,07 0,09 0,11 0,13 0,16 0,17 0,19 0,20 0,22 0,23 0,24 0,25 0,26 0,28 0,28 0,29 1,2 0,06 0,08 0,10 0,12 0,14 0,16 0,18 0,19 0„21 0,22 0,23 0,24 0,26 0,27 0,28 0,29 1,3 0,05 0,07 0,09 0,11 0,13 0,15 0,17 0,18 0,20 0,21 0,23 0,23 0,25 0,26 0,27 0,29 0,8 0,31 0,33 0,34 0,35 0,37 0,38 0,39 0,40 0,41 0,42 0,43 0,43 0,44 0,45 0,45 0,46 0,9 0,18 0,21 0,23 0,26 0,29 0,31 0,33 0,34 0,36 0,38 0,39 0,40 0,41 0,42 0,43 0,444 1,0 0,12 0,15 0,18 0,21 0,24 0,27 0,29 0,30 0,33 0,34 0,36 0,37 0,39 0,40 0,42 0,43 1,1 0,09 0,12 0,15 0,17 0,21 0,24 0,26 0,28 0,30 0,32 0,34 0,35 0,37 039 0,40 0,43 1,2 0,07 0,10 0,13 0,15 0,19 0,22 0,24 0,26 0,28 0,30 0,32 0,33 0,36 038 039 0,41 1,3 0,07 0,09 0,11 0,14 0,17 0,20 0,22 0,24 0,27 0,29 0,31 0,32 0,35 037 0,38 0,40 0,8 0,46 0,47 0,48 0,50 0,51 0,53 0,54 0,54 0,56 0,57 0,57 0,58 0,59 0,59 0,60 0,60 0,9 0,23 0,27 0,30 0,34 0,38 0,41 0,43 0,44 0,47 0,49 0,50 0,52 0,53 0,55 0,56 0,58 1,0 0,14 0,18 0,22 0,25 0,30 0,33 0,36 0,38 0,41 0,44 0,46 0,47 0,50 0,52 0,54 0,55 1,1 0,10 0,14 0,17 0,21 0,25 0,29 0,32 0,34 0,38 0,40 0,42 0,44 0,47 0,50 0,52 0,54 – 136 – φf es /ho 1,2 Коэффициент φс при значениях μas2, равных 0,03 0,05 0,07 0,10 0,15 0,20 0,25 0,30 0,40 0,50 0,60 0,70 0,90 1,10 1,50 2,00 0,10 0,11 0,14 0,18 0,22 0,26 0,29 0,31 0,35 0,38 0,40 0,42 0,45 0,48 0,50 0,52 ≥1,3 0,11 0,10 0,13 0,16 0,20 0,24 0,27 0,29 0,33 0,36 0,38 0,40 0,43 0,46 0,49 0,51 0,6 0,8 1,0 0,8 0,61 0,63 0,64 0,65 0,67 0,68 0,69 0,69 0,71 0,71 0,72 0,73 0,73 0,74 0,75 0,75 0,9 0,28 0,33 0,37 0,41 0,46 0,50 0,52 0,54 0,58 0,60 0,62 0,63 0,62 0,68 0,69 0,71 1,0 0,16 0,21 0,25 0,29 0,35 0,39 0,43 0,45 0,50 0,53 0,55 0,57 0,60 0,63 0,65 0,68 1,1 0,13 0,15 0,19 0,23 0,29 0,33 0,37 0,40 0,44 0,48 0,51 0,53 0,56 0,60 0,62 0,65 1,2 0,14 0,12 0,16 0,20 0,25 0,29 0,33 0,36 0,41 0,44 0,47 0,50 0,53 0,57 0,60 0,63 1,3 0,15 0,13 0,14 0,17 0,23 0,27 0,30 0,33 0,38 0,42 0,45 0,47 0,41 0,45 0,58 0,62 0,8 0,79 0,80 0,80 0,81 0,83 0,84 0,85 0,85 0,86 0,87 0,87 0,88 0,88 0,89 0,90 0,90 0,9 0,33 0,38 0,43 0,48 0,54 0,58 0,62 0,64 0,68 0,71 0,73 0,75 0,78 0,80 0,82 0,84 1,0 0,17 0,23 0,27 0,33 0,40 0,45 0,49 0,52 0,57 0,61 0,64 0,66 0,70 0,74 0,77 0,80 1,1 0,16 0,16 0,20 0,25 0,32 0,37 0,41 0,45 0,50 0,45 0,58 0,61 0,65 0,70 0,73 0,76 1,2 0,17 0,16 0,17 0,21 0,27 0,32 0,36 0,40 0,46 0,50 0,54 0,57 0,61 0,66 0,70 0,74 1,3 0,19 0,17 0,15 0,19 0,24 0,29 0,33 0,37 0,42 0,47 0,50 0,54 0,58 0,64 0,67 0,72 0,8 0,97 0,98 0,98 0,99 1,0 1,01 1,01 1,02 1,02 1,03 1,03 1,04 1,04 1,04 1,05 1,05 0,9 0,37 0,44 0,49 0,55 0,62 0,67 0,71 0,74 0,78 0,82 0,84 0,86 0,89 0,93 0,95 0,97 1,0 0,18 0,24 0,29 036 0,44 0,50 0,54 0,58 0,64 0,69 0,72 0,75 0,80 0,85 0,88 0,91 1,1 0,19 0,18 0,22 0,27 0,34 0,40 0,46 0,49 0,56 0,61 0,65 0,69 0,73 0,79 0,83 0,87 1,2 0,21 0,19 0,18 0,22 0,29 0,35 0,37 0,43 0,50 0,55 0,59 0,63 0,69 0,75 0,79 0,84 1,3 0,23 0,21 0,19 0,20 0,26 0,31 0,36 0,39 0,46 0,51 0,56 0,59 0,65 0,71 0,76 0,81 ϕf = (b ' f ) ( ) − b h'f − A'sp + As a s1 bh0 ; μa s 2 = Asp + As bh0 ; es M s = . h0 Ph0 Таблица П14 в зависимости от схемы b'f − b h'f − A'sp + Asb'f a−s1b h'f − A'spAsp+ +AsAsa s1 es балки и загружения 5 1 1 a2 1 1 a 3 − a − 2 l 48 12 8 коэффициента 4 3 6l 8l Значения S ( ϕf = Схема загружения Коэффисвободно опертой балки циент b'f S− b ϕf = ( ( 5 48 ) 1 12 ) ) ( ( () ) ( ) M ϕf = ; μa s 2 = ; ; μ=a s 2 =s bh0 bh0 bh0 h0 Ph0 Схема загружения Коэффициконсольной ент ' ' h'f − A'sp + Aбалки b a b h A'spspS++ AAss a se1s M s Asp − s f s1 f − A a ϕ = ; μ = ; ; =μa s 2 =. 2 2 1 abh 1 f 15 a 1 −1a sa2 bh 1 bh 1 a 3h− a Ph b 3 − 0 0 0 0 0 − 8 ( 8l 2 () 4 () 348 6l12 ) ) ( 8l 8l 2 ( ) 4 ) 3 6l l ' b'f − b h'f − A2'sp + Asb'fa s−1 b h'f − AA a e A + As ++AA M sp 2 sp a s sp 1 s 1s ; s1a;sμ ϕ f = 5 1 1 − a ϕ f 1= 1 5 a ;13μ−aas12−=a ; s 2 = . 3=a−Ph 2 2 bh bh bh h bh0 l 0 48 12 8 80l 4 3 486l 12 l8 80l 40 3 6l0 5 48 1 12 1 a2 − 8 8l 2 1 1 5 a 1 3 − 1a a 2 − 8l 8l 2 4 348 6l12 – 137 – 1 1 4 3 a a 3 − l 6l – 138 – Сортамент арматуры Таблица П15 Таблица П16 Сортамент арматурных канатов Класс каната К-7 К-19 Класс каната К-7 К-19 Номиналь- Теоретичесный диа- кая масса метр, мм 1 м, кг 6 9 12 15 14 0,173 0,402 0,714 1,116 1,014 Номиналь- Теоретичесный диа- кая масса 1 м, кг метр, мм 6 9 12 15 14 0,173 0,402 0,714 1,116 1,014 Расчетная площадь поперечного сечения арматурных канатов (мм2) при их числе 1 2 3 4 5 22,7 45,4 68,1 90,8 113,5 51 102 153 204 255 90,6 181,2 271,8 362,4 453 141,6 283,2 424,8 566,4 708 128,7 257,4 386,1 514,8 643,5 Расчетная площадь поперечного сечения арматурных канатов (мм2) при их числе 136,2 306 543,6 849,6 772 158,9 357 634,2 991,2 900,9 181,6 408 724,8 1132,8 1029,6 204,3 459 815,4 1274,4 1158,3 227,0 510 906 1416 1287 Таблица П17 Таблица для расчета многоэтажных многопролетных рам Ригели рамы на крайних опорах, жестко соединенные с колоннами Схема загружения и эпюры моментов k Опорные моменты М12 М21 М23 М32 0,5 -0,072 -0,090 -0,083 -0,083 1 -0,063 -0,091 -0,085 -0,085 2 -0,054 -0,093 -0,087 -0,087 3 -0,046 -0,095 -0,088 -0,088 4 -0,039 -0,097 -0,089 -0,089 5 -0,033 -0,099 -0,090 -0,090 6 -0,027 -0,100 -0,091 -0,091 – 139 – Схема загружения и эпюры моментов k 0,5 Опорные моменты М12 М21 М23 М32 -0,077 -0,079 -0,006 -0,006 1 -0,070 -0,074 -0,012 -0,012 2 -0,062 -0,068 -0,018 -0,018 3 -0,055 -0,065 -0,022 -0,022 4 -0,048 -0,063 -0,026 -0,026 5 -0,042 -0,063 -0,028 -0,028 6 -0,036 -0,062 -0,030 -0,030 0,5 0,005 -0,011 -0,077 -0,077 1 0,007 -0,017 -0,073 -0,073 2 0,008 -0,025 -0,069 -0,069 3 0,009 -0,030 -0,066 -0,066 4 0,009 -0,034 -0,063 -0,063 5 0,009 -0,036 -0,062 -0,062 6 0,009 -0,038 -0,061 -0,061 0,5 -0,071 -0,092 -0,088 -0,072 1 -0,062 -0,095 -0,094 -0,066 2 -0,052 -0,101 -0,098 -0,059 3 -0,045 -0,107 -0,100 -0,054 4 -0,037 -0,112 -0,102 -0,050 5 -0,032 -0,115 -0,104 -0,046 6 -0,026 -0,117 -0,105 -0,043 – 140 –