Структура Механизмов 2446

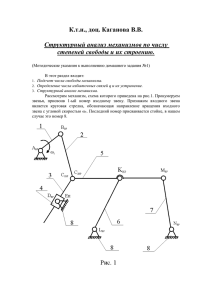
Украинской государственной академии
железнодорожного транспорта
Кафедра „ Высшая математика и физика ”
В. П. Шамота, А. Л. Фалько
Структура механизмов
Пособие по дисциплине «Теория механизмов і машин»
для студентов дневной и заочной форм обучения
специальности: 7.070501 «Локомотивы и локомотивное хозяйство»
Донецк - 2013
1
Методическое пособие по ТММ «Структура механизмов» рассмотрено и
рекомендовано к изданию и использованию в учебном процессе для студентов
специальности 7.070501 «Локомотивы и локомотивное хозяйство» на заседании
кафедры «Высшая математика и физика» 30 августа 2013 г., протокол № 1.
Составители:
Д.т.н., профессор
К.т.н., доцент
В. П. Шамота
А. Л. Фалько
Рецензенты:
Д.т.н., профессор
К.т.н., доцент
Заплетников И.Н. (ДонНУЭТ)
Тимохин Ю.В. (ДонИЖТ)
Председатель методической комиссии ДонИЖТ
К.т.н., доцент
Прилепский Ю.В.
2
1. Введение. Некоторые понятия ТММ
Теория механизмов и машин является общеинженерной дисциплиной,
которая вместе с курсами теоретической механики, сопротивления материалов и
деталей машин образует группу предметов, обеспечивающих фундамент
инженерного образования инженера – механика.
ТММ, используя законы теоретической механики, изучает методы
построения и исследования механизмов. Сведения, содержащиеся в курсе ТММ,
важны не только для конструкторов, но и для эксплуатационников, так как
грамотная эксплуатация возможна только при четком понимании принципов
работы и расчета машин.
ТММ решает 2 основные задачи: анализ и синтез механизмов и машин.
Анализ осуществляется при заданных размерах и массе звеньев, когда
необходимо определить: скорости, ускорения, действующие силы, напряжения в
звеньях и их деформации. В результате может быть произведен проверочный
расчет на прочность, выносливость и т.д.
Синтез осуществляется при заданных скоростях, ускорениях, действующих
силах, напряжениях или деформациях. При этом требуется определить
необходимые размеры звеньев, их форму и массу.
При синтезе часто решается задача оптимального проектирования
конструкции, когда требуется найти необходимые показатели работы машины при
наименьших затратах труда.
Само название курса указывает на то, что есть различие между понятиями
«механизм» и «машина». Содержание этих понятий изменялось в процессе
развития техники. К настоящему времени утвердились ниже следующие
определения.
Машина есть устройство, выполняющее механические движения для
преобразования энергии, материалов или информации с целью замены или
облегчения труда человека.
В состав каждой машины входит один или несколько механизмов.
Механизм – это система материальных тел, предназначенных для
преобразования движения одного или нескольких тел в требуемые движения
других тел.
В зависимости от того, в каком виде существуют тела передающие движение
– твердом, жидком или газообразном, механизмы принято делить на механизмы с
твердыми звеньями, гидравлические и пневматические. В курсе ТММ
рассматриваются только механизмы с твердыми звеньями, гидравлические и
пневматические механизмы подробно изучаются в специальных курсах.
Звеном называется одна или несколько жестко связанных между собой деталей.
Неподвижное звено называется стойкой или станиной. Движение остальных
звеньев механизма рассматривается относительно этого звена.
Входным звеном механизма называется звено, которому сообщается движение.
3
Выходным звеном называется звено, которое совершает движение, для которого
предназначен механизм.
Входное звено механизма соединено с двигателем, выходное – с рабочим органом
машины. Остальные звенья механизма называются промежуточными.
Кинематической парой называется соединение двух звеньев, допускающее их
относительное движение.
1. Виды кинематических пар
Из теоретической механики известно, что свободное твердое тело, находящееся в трехмерном пространстве, обладает 6-ю степенями свободы (Н=6), т.е.
может совершать 6 независимых движений: 3 поступательных вдоль выбранных
осей и 3 вращательных вокруг этих же осей. Если такое тело связать с другим
телом посредством кинематической пары, то это уменьшит его число степеней
свободы (Н) на число условий связи (S), налагаемых другим телом (Н=6-S). Число
условий связи (S) определяет класс пары (рs) и зависит от вида кинематической
пары (Рис. 1.1).
б)
а)
в)
S=2; H=4; p2
S=3; H=3; p3
S=1; H=5; p1
г)
S=4; H=2; p4
д) S=5; H=1; p5
Рис. 1.1
На рис. 1.1 стрелками указаны возможные направления вращательного или
поступательного перемещений, число которых соответствует числу степеней
свободы (Н). Помимо этого на рис. 1.1 а), б), в) стрелками показаны оси координат.
Следует отметить, что кинематические пары на рис. 1.1 а), б), в) имеют силовое
замыкание звеньев (силой гравитации), а на рис. 1.1 г), д) кинематические пары
имеют геометрическое замыкание звеньев (форма деталей мешает их выходу из
кинематической пары).
Примеры кинематических пар и их условные обозначения даны в табл. 1.1.
4
Табл. 1.1
Класс пары
(число условий,
связи S=6-H)
Число степеней Обозначение
свободы, Н
рs
(Н=6-S)
Принципиальная схема
Условное
обозначение
Шаровая опора
3
3
р3
4
2
р4
Вращательная пара
5
1
р5
Поступательная пара
5
1
р5
4
2
р4
Винтовая пара
5
1
р5
Кинематические пары также различают по числу степеней свободы на одно-,
двух-, трех-, четырех-, и пяти- подвижные. Подвижность (Н) и класс (рs) каждой
пары в сумме равны 6, т.е. числу степеней свободы свободного твердого тела.
Таким образом, класс и подвижность с разных сторон характеризуют одно и то же
свойство.
Наиболее распространены простейшие одноподвижные пары (5-й класс - р5):
поступательная и вращательная, которые накладывают 5 условий связей,
оставляя возможным только одно поступательное или одно вращательное
движение соответственно. Кинематические пары 5-го класса существуют в виде
поступательных, вращательных и винтовых. У винтовых пар вращательное и
поступательное движения связаны в одно движение по винтовой спирали, поэтому
эти пары также являются одноподвижными.
Кинематические пары по характеру движения делятся на плоские и
пространственные. В плоских парах (р5, р4) относительное движение звеньев
происходит в одной или в параллельных плоскостях.
Элементы кинематической пары – точки, линии, поверхности, по которым
происходит соприкосновение звеньев в кинематической паре.
По форме элементов кинематические пары делятся на низшие и высшие. В
низших парах (р5, иногда p4) элементами служат поверхности: плоскости,
цилиндрические и сферические поверхности (рис. 1.2 а). В высших парах
элементами являются точки и линии (рис. 1.2 б). Достоинство низших пар –
повышенная долговечность соединения (что сделало их наиболее широко
применимыми в технике), благодаря небольшим удельным нагрузкам на
5
а)
б)
Рис. 1.2
поверхность (большая площадь контакта). В
высших парах соприкосновение звеньев
происходит на небольших площадках, что
ведет
к
их
ускоренному
износу.
Посредством
низших
пар
можно
осуществлять
относительно
простые
движения, высшие пары представляют в
этом отношении большие возможности.
Например:
Дверные завесы – кинематическая пара: (р5), плоская,
низшая, вращательная,
условное изображение на чертеже схемы:
2. Кинематические цепи
Кинематическая цепь - это система звеньев, образующих между собой
кинематические пары.
Различают плоские и пространственные кинематические цепи. В плоской
кинематической цепи все звенья движутся в одной или параллельных плоскостях.
Кинематическая цепь, звенья которой образуют замкнутый контур,
называется
замкнутой, а если контур не замкнут, то цепь называется
незамкнутой или открытой. В традиционных механизмах обычно используются
замкнутые кинематические цепи, незамкнутые (открытые) цепи находят
применение только в манипуляторах.
Кинематические цепи делят на простые и сложные. В простой цепи
каждое звено входит в одну или в две кинематические пары, а в сложной цепи
имеются звенья, входящие в три и более кинематические пары.
Примеры схематичного изображения различных кинематических цепей даны
на рис. 2.1. Отрезками изображаются на схемах звенья, кружками – вращательные
кинематические пары 5-го класса (одноподвижные).
Рис. 2.1 Схемы плоских кинематических цепей:
а) простая незамкнутая (открытая) цепь;
б) простая замкнутая цепь;
в) сложная открытая цепь.
6
Механизм – это замкнутая кинематическая цепь, в которой есть стойка,
входные, промежуточные
и выходные звенья, совершающие заданные
движения.
Структурной
схемой
механизма (Рис. 2.2) называется
упрощенное
графическое
изображение
механизма,
на
котором звенья изображаются
условно
отрезками
прямых,
треугольниками,
прямоугольниками и обозначаются
арабскими цифрами, а кинематические пары также изображаются условно согласно
принятым правилам (например: окружностями) и обозначаются большими
латинскими буквами (например: А, В, С на рис. 2.2). Имеется соответствующий
стандарт, регламентирующий условные изображения звеньев и пар на схемах.
Кинематической схемой механизма называется структурная схема,
построенная с соблюдением относительных размеров звеньев в определенном
масштабе.
На рис. 2.2: звено 1 – кривошип – входное (ведущее, начальное) звено,
связано со стойкой, совершает вращательное движение с постоянной угловой
скоростью ω; звено 2 – шатун – совершает сложное (поступательное и
вращательное) движение, не связан со стойкой; звено 3 – ползун - совершает
поступательное движение по неподвижному звену; звено 4 – стойка –
неподвижное звено.
3. Степень подвижности механизма
Степень подвижности механизма – это число степеней свободы, т.е.
независимых между собой направлений поступательного или вращательного
движения, определяющих положение кинематической цепи механизма в
выбранном пространстве.
Пусть пространственная кинематическая цепь содержит n подвижных
звеньев. До того как они были соединены посредством кинематических пар,
система из n подвижных звеньев имела 6n степеней свободы. Каждая
кинематическая пара дает число связей относительно выбранной системы
координат равное своему классу (5p5, 4p4…). Разность между числом степеней
свободы звеньев до соединения в пары 6n и суммарным числом связей, налагаемых
каждой парой, дает число независимых координат всей цепи:
W= 6n - 5p5 - 4p4 - 3p3 - 2p2 - p1 - формула Сомова-Малышева,
где W – число степеней свободы механизма,
6 – число степеней свободы любого звена до вступления в пару
n – число подвижных звеньев механизма,
p5 – число пар 5-го класса (одноподвижных),
налагающих 5p5 связей,
7
р4 – число пар 4-го класса, налагающих 4p4 связей (двух- подвижных),
р3 – число пар 3-го класса, налагающих 3p3 связей (трех- подвижных).
…
Для плоских механизмов аналогичные рассуждения приводят к формуле
Чебышева:
W = 3n – 2p5 – p4 - формула Чебышева для плоских механизмов,
где W – число степеней свободы (степень подвижности) механизма;
3 – число степеней свободы любого звена в плоскости
до вступления в пару;
n – число подвижных звеньев механизма.
На рисунке 3.1 представлены примеры кинематических цепей с различными
степенями подвижности (пересчитайте самостоятельно по формуле Чебышева).
Рис 3.1
1
Рис.
Число степеней свободы механизма определяет число начальных (входных)
звеньев. Как правило, применяют механизмы с W = 1.
В механизмах с простой замкнутой кинематической цепью и
одноподвижными парами число подвижных звеньев на единицу меньше числа
кинематических пар (докажите это из формулы Чебышева).
Любой механизм имеет одно неподвижное звено (стойку) и «n» подвижных
звеньев.
Для
плоского
механизма
2
B
степень подвижности определяется
C
по формуле Чебышева.
Например,
1
кривошипно-ползунный
плоский
механизм (рис. 3.2), в котором есть
A
неподвижное звено - стойка (без
D
номера), соединенное через шарнир
3
Рис.7
Рис.
3.2
8
А с кривошипом 1, соединенным через шарнир В (шарнир – вращательная пара)
с шатуном 2, соединенным через шарнир С с ползуном 3, соединенным через
поступательную пару в точке D со стойкой. Подсчитаем: n=3; p5=4; p4=0, т.е.
W = 3n-2p5-p4 = 3·3 - 2·4 – 0 = 1.
Называют механизмы по подвижным начальному (входному) и конечному
(выходному) звеньям, например кривошипно-ползунный механизм (рис. 3.2,
рис. 2.2).
При
определении
W
необходимо
учитывать возможность наличия так называемых
избыточных (пассивных) звеньев и пар,
устранение которых не нарушает кинематики
анализируемого механизма. Так на рис. 3.3
шатун 4 и с ним две прилежащие
кинематические пары – избыточны, т.к. не
изменяют при их удалении законов движения
других звеньев. W = 3n-2p5-p4, т.е.:
Рис. 3.3
а) W=3·4-2·6-0=0 – с пассивным звеном 4,
б)
W=3·3-2·4-0=1
действительности), без учета избыточных звеньев и пар.
–
фактически
(в
4. Классификация плоских механизмов с низшими парами
Механизмы с низшими парами называют рычажными. Они находят
широкое применение в технике. Ограничимся изучением плоских рычажных
механизмов.
Основной принцип образования рычажных механизмов был сформулирован
в 1914 году профессором Л. В. Ассуром и заключается в следующем.
Схема любого механизма может быть составлена последовательным
присоединением к входным (начальным) звеньям и стойке кинематических цепей с
нулевой степенью подвижности. Такие кинематические цепи с W=0 называются
структурными группами Ассура.
Т.о механизм с W=1 рассматривают состоящим из механизма 1-го
класса (начальное звено и стойка) и присоединенных к нему структурных
групп с нулевой степенью подвижности (групп Ассура с W=0).
9
Механизмом 1-го класса 1-го порядка является начальное звено со
стойкой. Он имеет
W=1. (Рис. 4.1) Определение класса и порядка
кинематических цепей дано далее.
Рис. 4.1 Начальное звено и стойка: механизмы 1-го класса
На рисунке 4.1 а) указаны: 1- стойка, А – вращательная пара стойкакривошип, 2 – кривошип – звено, связанное со стойкой и совершающее
вращательное движение с постоянной угловой скоростью ω.
На рисунке 4.1 б) указаны: 1- стойка, С – поступательная пара стойкаползун, 3 – ползун – звено, совершающее поступательное движение по
неподвижному звену.
Структурной группой Ассура с W=0 называется такая группа звеньев,
которая, будучи присоединенной к стойке свободными концами, останется
неподвижной. Она не изменяет степени подвижности кинематической цепи, к
которой она присоединяется.
Выведем уравнение структурной группы Ассура с нулевой степенью
подвижности:
W= 3n – 2p5 - p4 = 0 , (p4=0), откуда p5 = 1.5n - уравнение структурной группы
Т.о., в структурной группе Ассура (W=0) число звеньев обязательно четное, а
число кинематических пар p5 в 1.5 раза больше числа звеньев. Задаваясь разным
n, можно получить бесконечно большое число структурных групп Ассура.
Практическое значение имеют только два первых решения. Им соответствует
двухповодковая группа (диада, n=2), и трехповодковая группа (трехповодок,
n=4). Диада содержит два звена (n=2) и три кинематические пары (p5=3).
Трехповодок содержит четыре звена (n=4) и шесть кинематических пар (p5=6)
(Табл. 4.1).
10
Табл. 4.1
n
p5
Группы звеньев Ассура (с W=0), имеющие практическое значение
Диады-группы 2 класса 2 порядка:
1 вида
2
2 вида
3 вида
4 вида
5 вида
3
Вид диады зависит от различных комбинаций расположения
поступательных и вращательных пар между двумя звеньями
Трехповодок: группа
3-го класса, 3-го порядка
4
Группа Ассура
4-го класса 2-го порядка
6
Если группу с нулевой степенью подвижности (группу Ассура) присоединить
свободными концами через кинематические пары к неподвижному звену, то такая
группа (с W=0) станет неподвижной.
По предложению академика И. И. Артоболевского группам и механизмам
присвоены классы.
Класс группы равен числу кинематических пар, входящих в замкнутый
контур, образованный внутренними парами.
Диаду принято считать группой 2-го класса 2го порядка, а трехповодок
является группой 3-го класса (3 порядка).
Порядок группы определяется числом элементов звеньев, которыми
группа присоединяется к механизму.
Класс всего механизма равен наибольшему классу входящей в него
группы.
11
5. Разновидности плоских рычажных механизмов
Последовательно присоединяя к механизму 1-го класса группу за группой
(Ассура с W=0), можно получить разные механизмы. Практическое применение
находят механизмы 2-го (с диадами) и реже – 3-го класса.
В технике наибольшее распространение получили плоские четырехзвенные
механизмы. Они образуются путем присоединения к механизму 1-го класса диады.
За счет разного сочетания вращательных и поступательных пар в диаде возникают
модификации групп Ассура.
Известно пять видов двухповодковых групп Ассура (диад), соответственно
этому имеются модификации четырехзвенных механизмов, представленные в
таблице 5.1
Табл. 5.1
Диады – группы звеньев 2-го класса, 2-го порядка
1-й вид.
2-й вид.
3-й вид.
4-й вид.
5-й вид.
Механизмы, образуемые присоединением диады к механизму 1-го класса: кривошипу и стойке
Шарнирный
четырехзвенник
Кривошипноползунный
механизм
Кулисный
механизм
Тангенциальный
Синусный
механизм
механизм
Механизм
Ольдгейма
а) кривошипнокоромысловый
б) двухкривошипный
Крестовая
муфта
в) двухкоромысловый
Механизм с диадой 1-го вида – шарнирный четырехзвенник. Он
применяется для изменения параметров вращательного движения или для
воспроизведения сложных траекторий. В зависимости от соотношения размеров
стойки и остальных звеньев возможны три разновидности шарнирного
12
четырехзвенника:
кривошипно-коромысловый
двухкривошипный механизм, двухкоромысловый.
механизм
(рис.
5.1),
Звеньям этих механизмов присвоены специальные названия (по рис. 5.1): 1 –
кривошип – звено, совершающее вращение на полный поворот с постоянной
угловой скоростью; 2 – шатун – звено, не образующее кинематических пар со
стойкой 4, совершающее сложное плоскопараллельное движение; 3 – коромысло
– звено, совершающее неполный поворот (качательное движение).
Правило Гросгоффа: условие проворачиваемости кривошипа в шарнирном
четырехзвеннике (по рис. 5.1). Кривошип может делать полный оборот, если
сумма длин двух других подвижных звеньев (b+c) больше суммы длин
кривошипа и стойки (a+d).
Механизм с диадой 2-го вида – кривошипно-ползунный (рис. 2.2, рис.
3.2). Он применяется для преобразования вращательного движения в
поступательное и обратно. Ползун – звено, образующее поступательную пару со
стойкой (направляющей ползуна).
Механизм с диадой
3-го вида – кулисный. Кулисные механизмы
предназначены для изменения параметров вращательного движения.
Кулиса ( рис. 5.2) – звено 3, связанное со стойкой,
2
совершающее качательное или вращательное движение,
3
образующее с другим подвижным звеном - кулисным
1
камнем 2, поступательную пару.
Кулисный камень – звено 2, совершающее
4 сложное движение: поступательное – вдоль кулисы в
Рис. 5.2
качестве подвижной направляющей и вращательное –
относительно неподвижного шарнира кулисы.
13
Механизм с диадой 4-го вида получил название тангенциального
механизма, т.к. перемещение ведомого звена представляет функцию tgφ.
Механизм с диадой 5-го вида – синусный
2
механизм (рис. 5.3), т.к. перемещение ведомого звена
реализует функцию sinφ. Присоединяя диаду 5-го вида к
1
механизму 1-го класса другим способом, можно получить
механизм Ольдгейма (крестовую муфту), который
находит применение для передачи движения при
4
несоосных валах.
3
Рис. 5.3
Список рекомендуемой литературы по дисциплине
“Теория механизмов и машин”
1. Артоболевский И. И. ТММ./учебник для вузов/.-4-е изд., перераб. и доп.-М.:
Наука, 1988.
2. Артоболевский И. И. Сборник задач по ТММ./для машин. Спец.вузов/2-е изд.,
стереотипное.-М.:Наука, 1975,1973.
4. Безвесельный Е. С. Курсовое проектирование по ТММ в примерах. -Харьков:
изд-во Харьк.ун-та, 1960.
5. Безвесельный Е. С. Вопросы и задачи по ТММ:-Киев, 1977.
6. Белоконев И. М. ТММ: Методы автоматизированного проектирования. Уч.
пособие для техн.вузов.-Киев:Выща школа, 1990.
7. Ковалев Н. А. ТММ и детали машин. Краткий курс/для немашин. спец.
вузов/изд-е 2-е, испр.-М.: Высш.шк., 1973.
8. Кореняко А. С. ТММ. Учебник для втузов. Изд.3-е, перераб.-Киев:Выща Щкола,
1976.
10. Курсовое проектирование по ТММ. Уч.пособие для механ. И машиностр. Спец.
вузов. Под ред. А. С. Кореняко-М.-Л.:Машин-е, 1964, 1970.
11. Левитская О. Н., Левитский Н. И. Курс ТММ./Уч.пособие для механ.спец.
вузов/ 2-е изд., перераб. и доп.-М.:Наука, 1990.
12. Машнев М. М. ТММ и детали машин./Уч.пособие для немашин.спец. вузов/2-е
изд., перераб. и доп., Л.: Машин-е,1980.
14
Шамота В.П.
Фалько А.Л.
Структура механизмов
Пособие по дисциплине «Теория механизмов и машин»
для студентов дневной и заочной форм обучения
специальности: 7.100501 «Локомотивы и локомотивное хозяйство»
15