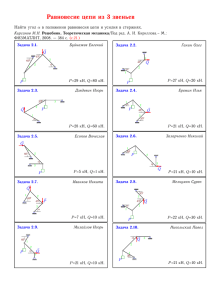
1 вариант 1. Студент может доехать до института либо автобусом, либо троллейбусом. Автобусы следуют с интервалом в 10 мин, троллейбусы – с интервалом в 7 мин. Найти вероятность того, что студент будет ждать автобус или троллейбус не более 4 мин. 2. Имеются две урны. В первой 3 белых и 4 черных шаров; во второй 5 белых и 3 черных шаров. Некто подходит наугад к одной из урн и вынимает из нее один шар. Шар оказался белым. Найти вероятность того, что этот шар был вынут из первой урны. 3. Мишень состоит из двух секторов. Вероятность попадания при одном выстреле в первый сектор равна 0,4; во второй – 0,3; вероятность непопадания в мишень равна 0,3. Найти вероятность того, что при пяти выстрелах будет по два попадания в первый и во второй секторы и один промах. 4. Вероятность попадания в цель при каждом выстреле равна 0,005. Найти вероятность попадания в цель не менее трех раз, если число выстрелов равно 800. 5. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва цепи в течение этого срока. p2 = p4 = p6 = 0.8 . p1 = p3 = p5 = p7 = 0.9 , 2 вариант 1. На десяти карточках написаны цифры от 0 до 9. Опыт состоит в случайном выборе (без возвращения) трех карточек и раскладывании их в порядке поступления в ряд слева направо. Найти вероятность того, что появится число, содержащее нечетные цифры. 2. Имеются три урны. В первой и второй урнах а белых и b черных шаров; а в третьей a белых и столько же черных. Некто подходит наугад к одной из урн и вынимает из нее два шара. Найти вероятность того, что оба шара белые (рассмотрите случаи: a = 1 , a 1 ). 3. Вероятность приема радиосигнала при каждой передаче равна 0,8. Найти вероятность того, что при пятикратной передаче сигнал будет принят менее 2 раз. 4. Аппаратура состоит из 1000 элементов, каждый из которых независимо от остальных выходит из строя за время t с вероятностью 5 10−4 . Найти вероятность того, что за время t откажет хотя бы один элемент. 5. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва цепи в течение этого срока. p2 = p4 = p6 = 0.8 . p1 = p3 = p5 = p7 = 0.9 , 3 вариант 1. На десяти карточках написаны цифры от 0 до 9. Опыт состоит в случайном выборе трех карточек (без возвращения) и раскладывании их в порядке поступления в ряд слева направо. Найти вероятность того, что появится число, содержащее хотя бы одну из цифр 4 или 5. 2. Имеются две урны. В первой 5 белых и 2 черных шаров; во второй 3 белых и 4 черных. Из первой урны во вторую перекладывают один шар. После этого из второй урны извлекают наугад один шар. Найти вероятность того, что он будет черным. 3. Вероятность приема радиосигнала при каждой передаче равна 0,8. Найти вероятность того, что при десятикратной передаче сигнал будет принят не менее трех раз. 4. Вероятность рождения мальчика равна 0,512. Считая применимым теоремы МуавраЛапласа, вычислить вероятность того, что среди 100 новорожденных больше мальчиков, чем девочек. 5. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва цепи в течение этого срока. p2 = p4 = p6 = 0.8 . p1 = p3 = p5 = p7 = 0.9 , 4 вариант 1. Из колоды в 36 карт наудачу вынимают без возвращения 8 карт. Найти вероятность того, что появятся 4 туза. 2. Прибор состоит из двух последовательно включенных узлов. Вероятность отказа первого узла равна 0.8, а второго – 0.7. Зав время испытаний прибора был зарегистрирован его отказ. Найти вероятность того, что отказал только первый узел. 3. В урне находится 10 белых и 5 черных шаров. Наудачу вынимаются с возвращением 10 шаров. Найти вероятность того, что будет вынуто не менее одного белого шара. 4. Вероятность того, что наугад взятое изделие окажется пригодным без доводки, равна 0,97. Контролер проверяет 400 изделий. Если среди них окажется 16 или более нуждающихся в доводке, вся партия возвращается на доработку. Найти вероятность того, что партия изделий будет принята. 5. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва цепи в течение этого срока. p2 = p4 = p6 = 0.8 . p1 = p3 = p5 = p7 = 0.9 , 5 вариант 1. Из колоды в 36 карт вынимают без возвращения 6 карт. Найти вероятность того, что ровно две карты тузы и две карты - короли. 2. Из урны содержащей 6 белых и 4 черных шаров наудачу отобрали (без возвращения) 3 шара. Шар, взятый наудачу из этих трех, оказался белым. Найти вероятность того, что два других шара тоже белые. 3. Опыт заключается в подбрасывании трех игральных костей. Найти вероятность того, что в шести независимых опытах комбинация "2 шестерки" появится не менее одного раза. 4. Вероятность выхода из строя одного элемента устройства, в течение t часов работы, равна 0,002. Найти вероятность того, что за время t из 1500 независимо работающих элементов выйдет из строя не более 2 элементов. 5. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва цепи в течение этого срока. p2 = p4 = p6 = 0.8 . p1 = p3 = p5 = p7 = 0.9 , 6 вариант 1. Брошено 10 игральных костей. Найти вероятность события: выпадет 4 шестерки и пять пятерок. 2. На елочный базар поступают елки с трех лесхозов, причем 1-ый лесхоз поставил 50 % елок, 2-й – 30 %, 3-й – 20 %. Среди елок 1-го лесхоза 10 % голубых, 2-го – 20 %, 3-го – 30 %. Куплена одна елка. Она оказалась голубой. Найти вероятность того, что она поставлена 2-м лесхозом. 3. В ячейку памяти ЭВМ записывается 8-разрядное двоичное число. Значения 0 и 1 в каждом разряде появляются с равной вероятностью. Найти вероятность того, что в двоичном числе количество единиц будет больше 4. 4. Телеграфная станция передает текст. В силу наличия помех каждый знак может быть неправильно принят с вероятностью 0,01. Найти вероятность того, что в принятом тексте, содержащем 1000 знаков, будет меньше 10 ошибок. 5. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва цепи в течение этого срока. p2 = p4 = p6 = 0.8 . p1 = p3 = p5 = p7 = 0.9 , 7 вариант 1. Из урны, содержащей 6 белых и 4 черных шара, вынимают без возвращения 4 шара. Найти вероятность того, что два шара белые и два – черные. 2. Из 1000 ламп 100 принадлежат 1-й партии, 250 – 2-й и остальные – 3-й партии. В 1-й партии 6 %, во 2-й – 5 %, в 3-й – 4 % бракованных ламп. Наудачу выбирается одна лампа. Найти вероятность того, что выбранная лампа бракованная. 3. В урне содержится 8 белых, 4 красных и 3 черных шара. Производится 5 извлечений с возвращением по одному шару. Найти вероятность того, что в результате извлечений появилось 3 белых шара и по одному остальных цветов. 4. Производятся независимые испытания, в каждом из которых событие А появляется с вероятностью 0,8. Найти вероятность того, что событие А произойдет в большинстве из 50 испытаний. 5. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва цепи в течение этого срока. p2 = p4 = p6 = 0.8 . p1 = p3 = p5 = p7 = 0.9 , 8 вариант 1. На отрезке [0,1] наудачу ставятся две точки. Найти вероятность события: расстояние между двумя точками меньше половины длины отрезка. 2. В магазин поступают одинаковые изделия с трех заводов, причем 1-й завод поставил 50 изделий, 2-й – 30, 3-й – 20 изделий. Среди изделий 1-го завода 70 % первосортных, а среди изделий 2-го – 80 %, 3-го – 90 % первосортных. Куплено одно изделие. Оно оказалось первосортным. Найти вероятность того, что это изделие выпущено 2-м заводом. 3. По каналу связи передается 20 знаков, каждый из которых, независимо от других, может быть искажен с вероятностью 0,01. Найти вероятность того, что будет искажено не более двух знаков. 4. Корректура в 500 страниц содержит 2000 опечаток. Найти наиболее вероятное число опечаток на одной странице и вероятность этого числа. 5. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва цепи в течение этого срока. p2 = p4 = p6 = 0.8 . p1 = p3 = p5 = p7 = 0.9 , 9 вариант 1. Бросаются одновременно две игральные кости. Найти вероятность того, что сумма выпавших очков равна 8. 2. Приборы одного вида изготавливаются тремя заводами: первый завод поставляет 1/3 всех изделий, второй – 1/4, оставшиеся изделия поставляются 3-им заводом. Надежность прибора, изготовленного первым заводом, равна 0,9; второго – 0,95; третьего – 0,85. Определить полную надежность прибора, поступающего на производство. 3. Что вероятнее выиграть у равносильного противника: три партии из четырех или пять из восьми? 4. Система, состоящая из 100 элементов, работает нормально, если за рассматриваемый период выйдет из строя не более трех элементов. Найти вероятность нормальной работы системы, если отказы элементов независимы и вероятности их отказов равны 0,02. 5. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва цепи в течение этого срока. p2 = p4 = p6 = 0.8 . p1 = p3 = p5 = p7 = 0.9 , 10 вариант 1. Из ящика, содержащего 20 теннисных мячей (12 новых и 8 старых), пятеро спортсменов взяли по одному мячу. Найти вероятность того, что среди отобранных мячей ровно два новых. 2. Имеются три урны. В первой 2 белых и 3 черных шаров; во второй 4 белых и 2 черных шаров; в третьей одни белые. Некто подходит наугад к одной из урн и вынимает из нее один шар. Шар оказался белым. Найти вероятность того, что этот шар был вынут из третьей урны. 3. Считая, что в среднем 15% открывающихся малых предприятий становятся в течение года банкротами, найти вероятность того, что из 10 новых малых предприятий за это время банкротами станут не более трех предприятий. 4. По каналу связи передано 100 символов. Искажение одного символа происходит с вероятностью 0,05. Найти вероятность того, что будет искажено менее двух символов. 5. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва цепи в течение этого срока. p2 = p4 = p6 = 0.8 . p1 = p3 = p5 = p7 = 0.9 , 11 вариант 1. Брошены две игральные кости. Найти вероятность того, что выпала хотя бы одна шестерка, при условии, что сумма очков равна 10. 2. Программа экзамена содержит 40 вопросов, из которых студент знает 30. Для успешной сдачи экзамена достаточно ответить на 3 вопроса или на два из них и на один дополнительный вопрос. Какова вероятность того, что студент успешно сдаст экзамен? 3. Вероятность отказа каждого прибора при испытании не зависит от отказов других приборов и равна 0,1. Испытано 9 приборов. Что вероятнее: откажет 3 или 5 приборов? 4. Известно, что левши в среднем составляют 1% населения. Используя формулы Пуассона и Муавра-Лапласа, найти вероятность того, что среди 100 человек не более пяти левшей. 5. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва цепи в течение этого срока. p1 = p3 = p5 = p7 = 0.9 , p2 = p4 = p6 = 0.8 . 12 вариант 1. В группе из 28 студентов четверть родились летом. Наудачу отобрали четырех студентов. Найти вероятность того, что среди отобранных двое родилось летом. 2. В коробке находится 8 новых и 4 игранных мячей. Для первой игры берут два мяча из коробки. Затем после игры их возвращают обратно. Найти вероятность того, что для второй игры будут вынуты два новых мяча. 3. Проведено 8 независимых испытаний, каждое из которых заключается в одновременном подбрасывании двух монет. Найти вероятность того, что в трех испытаниях из восьми появится по два герба. 4. По цели производится 100 независимых выстрелов. Вероятность попадания в цель при одном выстреле равна 0,04. Найти вероятность того, что в цель не попадет ни один снаряд. 5. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва цепи в течение этого срока. p1 = p3 = p5 = p7 = 0.9 , p2 = p4 = p6 = 0.8 . 13 вариант 1. Какова вероятность того, что в четырехзначном номере автомобиля в городе сумма первых двух цифр равна 7. 2. Вероятность обнаружения дефекта в дефектном изделии равна 0,8. Вероятность принять стандартное изделие за дефектное равна 0,05. Известно, что доля дефектных изделий равна 0,05. Найти условную вероятность того, что изделие удовлетворяет стандарту, если оно было признано дефектным. 3. Проведено 10 независимых испытаний, каждое из которых заключается в одновременном подбрасывании двух монет. Найти вероятность того, что не менее двух раз выпадет два герба. 4. Вероятность отказа датчика в течение месяца равна 0,1. Раз в месяц осматривают 1000 датчиков. Найти вероятность того, что откажет не более 122 датчиков. 5. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва цепи в течение этого срока. p1 = p3 = p5 = p7 = 0.9 , p2 = p4 = p6 = 0.8 . 14 вариант 1. Какова вероятность того, что четырехзначный номер автомобиля в городе имеет только две одинаковые цифры. 2. Среди четырех неразличимых по внешнему виду урн три урны имеют одинаковый состав шаров – два белых и один черный, а в четвертой урне – один белый и один черный шар. Из случайно выбранной урны наудачу извлекают один шар. Найти вероятность того, что этот шар – белый. 3. Найти вероятность того, что за десять подбрасываний пары игральных костей не менее двух раз выпадет сочетание «одна шестерка-одна пятерка». 4. Вероятность изготовления доброкачественного изделия равна 0,9. Найти вероятность того, что среди взятых наудачу 300 изделий не менее 99% окажется доброкачественных. 5. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва цепи в течение этого срока. p2 = p4 = p6 = 0.8 . p1 = p3 = p5 = p7 = 0.9 , 15 вариант 1. В урне содержится 3 белых и 4 черных шаров. Из нее последовательно вынимают два шара. Если первый шар оказывается черным, то в нее добавляют один белый шар. В противном случае состав шаров не меняют. Какова вероятность того, что один шар будет белым. 2. В ящике 6 билетов, среди которых два выигрышных. Найти вероятность того, что выбранный билет выигрышный. Решить эту же задачу, если перед извлечением один билет (неизвестно какой) был утерян. 3. На АТС могут поступать вызовы трех типов. Вероятности поступления вызовов 1-го, 2-го и 3-го типа соответственно равны 0,2; 0,3; 0,5. Поступило три вызова. Найти вероятность того, что все они разных типов. 4. Контрольную работу по теории вероятностей успешно выполняют в среднем 60% студентов. Какова вероятность того, что из 300 студентов работу успешно выполняют не менее 150 студентов. 5. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва цепи в течение этого срока. p2 = p4 = p6 = 0.8 . p1 = p3 = p5 = p7 = 0.9 , 16 вариант 1. Два парохода должны подойти к одному и тому же причалу. Время прихода обоих пароходов независимо и равновозможно в течение интервала времени 10 часов. Найти вероятность того, что первому пароходу придется ждать освобождения причала, если время стоянки первого парохода – 1 час, время стоянки второго – 2 часа. 2. Среди четырех неразличимых по внешнему виду урн три урны имеют одинаковый состав шаров – два белых и один черный, а в четвертой урне – один белый и один черный шар. Из случайно выбранной урны наудачу извлекают один шар. Найти вероятность того, что этот шар был из урны с составом шаров «два белых, один черный», если известно, что вынутый шар оказался белым. 3. Что вероятнее выиграть у равносильного противника: одну из двух партий или две из четырех? 4. Среднее число вызовов, поступающих на АТС в минуту, равно 120. Найти вероятность то, что за три секунды на АТС поступит не менее трех вызовов. 5. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва p2 = p4 = p6 = 0.9 . цепи в течение этого срока. p1 = p3 = p5 = p7 = 0.8 , 17 вариант 1. В телефонном номере три последние цифры стерлись. Считая, что все возможные значения стершихся цифр равновероятны, найти вероятность события: среди стершихся цифр хотя бы две различны. 2. В первой урне содержится 1 белый и 2 черных шаров, во второй урне – 4 белых и 1 черный. В третью урну кладут один шар, случайно выбранный из первой урны и один шар, случайно выбранный из второй. Найти вероятность извлечь белый шар из третьей урны. 3. На АТС могут поступать вызовы трех типов. Вероятности поступления вызовов 1-го, 2-го и 3-го типа соответственно равны 0,2; 0,3; 0,5. Поступило три вызова. Найти вероятность того, что среди них нет вызова 2-го типа. 4. Всхожесть семян данного сорта растений составляет 70%. Найти вероятность того, что из 700 посаженных семян число проросших будет больше 450. 5. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва цепи в течение этого срока. p2 = p4 = p6 = 0.9 . p1 = p3 = p5 = p7 = 0.8 , 18 вариант 1. Из 30 чисел 1, 2, …, 30 случайным образом без повторений отобрано 10 чисел. Найти вероятность того, что ровно 5 чисел делится на 3. 2. В пункте проката имеется 8 новых и 10 подержанных автомобилей. 2 машины взяли наудачу в прокат и спустя некоторое время вернули. После этого снова наудачу взяли два автомобиля. Какова вероятность того, что оба автомобиля новые. 3. По каналу связи передается 7 сообщений, каждое из которых, независимо от других, может быть искажено с вероятностью 0,15. Найти вероятность того, что будет правильно принято не менее двух сообщений. 4. Какова вероятность того, что из 2450 ламп, освещающих улицу, к концу года будет гореть от 1500 до 1600 ламп? Считать, что каждая лампа будет гореть в течение года с вероятностью 0,64. 5. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва p2 = p4 = p6 = 0.9 . цепи в течение этого срока. p1 = p3 = p5 = p7 = 0.8 , 19 вариант 1. 7 яблок, 3 апельсина и 5 лимонов раскладываются случайным образом в три пакета так, чтобы в каждом было одинаковое число фруктов. Какова вероятность, что все лимоны попали в один из пакетов. 2. В продажу поступила партия запасных деталей, произведенных на трех станках. Известно, что 50% продукции произведено на первом станке, а 20% – на втором. Среди деталей, произведенных на первом станке, 4% бракованных, среди деталей, произведенных на втором станке, 1% бракованных, и среди деталей, произведенных на третьем станке, 2% бракованных. Найти вероятность того, что купленная деталь оказалась бракованной. 3. Производится 5 независимых выстрелов по некоторой цели. Вероятность попадания при одном выстреле равна 0,8. Найти вероятность того, что будет хотя бы одно попадание. 4. Книга издана тиражом 10000 экземпляров. Вероятность того, что книга будет сброшюрована неправильно, равна 0,0002. Найти вероятность того, что тираж содержит менее 5 бракованных книг. 5. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва цепи в течение этого p2 = p4 = p6 = 0.9 . срока. p1 = p3 = p5 = p7 = 0.8 , 20 вариант 1. Из 30 чисел 1, 2, …, 30 случайным образом без повторений отобрано 10 чисел. Найти вероятность того, что все числа четные. 2. Перед посевом 80% всех семян было обработано ядохимикатами. Вероятность поражения растений, проросших из этих семян, вредителями равна 0,06, а растений, проросших из необработанных семян – 0,3. Какова вероятность того, что взятое наудачу растение окажется пораженным? Если оно пораженное, то какова вероятность того, что оно выращено из обработанного семени? 3. Вероятность выхода на линию каждого из 18 автобусов равна 0,9. Какова вероятность нормальной работы автобазы в течение дня, если для этого необходимо иметь на линии не менее 15 автобусов? 4. Стрелок сделал 80 выстрелов; вероятность попадания при каждом выстреле равна 0,7. Найти вероятность того, что число попаданий будет заключено между 50 и 60. 5. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва цепи в течение этого срока. p1 = p3 = p5 = p7 = 0.8 , p2 = p4 = p6 = 0.9 . 21 вариант 1. В урне содержится 3 белых и 2 черных шара. Из нее последовательно извлекают два шара. Если первый шар будет черным, то в урну добавляют один белый шар. В противном случае состав шаров не меняют. Найти вероятность того, что будут извлечены два черных шара. 2. На склад с оружием совершают налет четыре самолета. Вероятность поражения самолета системой ПВО равна 0,8. При прорыве k самолетов атакуемый объект (склад) будет уничтожен с вероятностью p k . Найти вероятность уничтожения склада. 3. Каждый из десяти аспирантов группы случайным образом и независимо от остальных выбирает один из четырех дней наступающей недели (понедельник, вторник, среда или четверг) для работы в библиотеке. Найти вероятность того, что в понедельник в библиотеку явится 3 аспиранта, а во вторник семь. 4. Всхожесть семян данного сорта растений составляет 70%. Найти вероятность того, что из 700 посаженных семян будет 500 проросших. 5. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва цепи в течение этого срока. p2 = p4 = p6 = 0.9 . p1 = p3 = p5 = p7 = 0.8 , 22 вариант 1. Среди кандидатов в студенческий совет факультета 3 первокурсника, 5 второкурсников и 7 третьекурсников. Из этого состава наудачу отбирают пять человек на предстоящую конференцию. Найти вероятность того, что не будет выбрано ни одного второкурсника. 2. Имеются две урны с шарами. В 1-й находится 3 белых и 4 черных шара, во второй – 2 белых и 3 черных. Из первой урны был утерян один шар, неизвестно какой. Затем из наудачу выбранной урны извлекли один шар. Найти вероятность того, что он белый. 3. Каждый из десяти аспирантов группы случайным образом и независимо от остальных выбирает один из четырех дней наступающей недели (понедельник, вторник, среда или четверг) для работы в библиотеке. Найти вероятность того, что в понедельник в библиотеку явится 1 аспирант, во вторник – 2, в среду 3, в четверг – 4. 4. Какова вероятность того, что среди 200 наудачу взятых изделий окажется не более 5 некачественных, если некачественные изделия составляют 2% всей продукции цеха. 5. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва p2 = p4 = p6 = 0.9 . цепи в течение этого срока. p1 = p3 = p5 = p7 = 0.8 , 23 вариант 1. Найти вероятность того, что в группе из 10 человек хотя бы два родились в один месяц. 2. Батарея из трех орудий произвела залп, причем два снаряда попали в цель. Найти вероятность того, что третье орудие попало, если вероятности попадания в цель 1-м, 2-м и 3м орудиями соответственно равны 0,5; 0,3; 0,4. 3. Опыт заключается в бросании трех игральных костей. Найти вероятность того, что в шести независимых опытах ровно 3 раза выпадет по три шестерки. 4. Какова вероятность того, что среди 200 наудачу взятых изделий окажется два или три некачественных изделия, если некачественные изделия составляют 2% всей продукции цеха. 5. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва цепи в течение этого срока. p2 = p4 = p6 = 0.9 . p1 = p3 = p5 = p7 = 0.8 , 24 вариант 1. Колода в 36 карт наудачу раздается двум игрокам. Найти вероятность того, что все карты пиковой масти достанутся одному игроку. 2. В первой урне содержится 3 белых и 2 черных шаров, а во второй урне – 4 белых и 1 черный. В пустую третью урну кладут 1 шар, случайно выбранный из первой урны, и 2 шара, случайно выбранных из второй. Найти вероятность того, что шар, вынутый из третьей урны, будет черным. 3. В семье 6 детей. Найти вероятность того, что в данной семье не менее двух мальчиков, но не более четырех. Считать вероятность рождения мальчика и девочки равными 0,5. 4. Из урны, содержащей 2 белых и 3 черных шара, по схеме выбора с возвращением вынимают 2400 шаров. Найти приближенную вероятность того, что число появлений белого шара заключено между 948 и 972. 5. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва p2 = p4 = p6 = 0.9 . цепи в течение этого срока. p1 = p3 = p5 = p7 = 0.8 , 25 вариант 6. На десяти карточках написаны цифры от 0 до 9. Опыт состоит в случайном выборе трех карточек (без возвращения) и раскладывании их в порядке поступления в ряд слева направо. Найти вероятность того, что появится число, содержащее хотя бы одну из цифр 4 или 5. 7. Имеются две урны. В первой 5 белых и 2 черных шаров; во второй 3 белых и 4 черных. Из первой урны во вторую перекладывают один шар. После этого из второй урны извлекают наугад один шар. Найти вероятность того, что он будет черным. 8. Вероятность приема радиосигнала при каждой передаче равна 0,8. Найти вероятность того, что при десятикратной передаче сигнал будет принят не менее трех раз. 9. Вероятность рождения мальчика равна 0,512. Считая применимым теоремы МуавраЛапласа, вычислить вероятность того, что среди 100 новорожденных больше мальчиков, чем девочек. 10. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва цепи в течение этого срока. p2 = p4 = p6 = 0.8 . p1 = p3 = p5 = p7 = 0.9 , 26 вариант 6. Из колоды в 36 карт наудачу вынимают без возвращения 8 карт. Найти вероятность того, что появятся 4 туза. 7. Прибор состоит из двух последовательно включенных узлов. Вероятность отказа первого узла равна 0.8, а второго – 0.7. Зав время испытаний прибора был зарегистрирован его отказ. Найти вероятность того, что отказал только первый узел. 8. В урне находится 10 белых и 5 черных шаров. Наудачу вынимаются с возвращением 10 шаров. Найти вероятность того, что будет вынуто не менее одного белого шара. 9. Вероятность того, что наугад взятое изделие окажется пригодным без доводки, равна 0,97. Контролер проверяет 400 изделий. Если среди них окажется 16 или более нуждающихся в доводке, вся партия возвращается на доработку. Найти вероятность того, что партия изделий будет принята. 10. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва цепи в течение этого срока. p2 = p4 = p6 = 0.8 . p1 = p3 = p5 = p7 = 0.9 , 27 вариант 6. Из колоды в 36 карт вынимают без возвращения 6 карт. Найти вероятность того, что ровно две карты тузы и две карты - короли. 7. Из урны содержащей 6 белых и 4 черных шаров наудачу отобрали (без возвращения) 3 шара. Шар, взятый наудачу из этих трех, оказался белым. Найти вероятность того, что два других шара тоже белые. 8. Опыт заключается в подбрасывании трех игральных костей. Найти вероятность того, что в шести независимых опытах комбинация "2 шестерки" появится не менее одного раза. 9. Вероятность выхода из строя одного элемента устройства, в течение t часов работы, равна 0,002. Найти вероятность того, что за время t из 1500 независимо работающих элементов выйдет из строя не более 2 элементов. 10. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва цепи в течение этого срока. p2 = p4 = p6 = 0.8 . p1 = p3 = p5 = p7 = 0.9 , 28 вариант 6. Брошено 10 игральных костей. Найти вероятность события: выпадет 4 шестерки и пять пятерок. 7. На елочный базар поступают елки с трех лесхозов, причем 1-ый лесхоз поставил 50 % елок, 2-й – 30 %, 3-й – 20 %. Среди елок 1-го лесхоза 10 % голубых, 2-го – 20 %, 3-го – 30 %. Куплена одна елка. Она оказалась голубой. Найти вероятность того, что она поставлена 2-м лесхозом. 8. В ячейку памяти ЭВМ записывается 8-разрядное двоичное число. Значения 0 и 1 в каждом разряде появляются с равной вероятностью. Найти вероятность того, что в двоичном числе количество единиц будет больше 4. 9. Телеграфная станция передает текст. В силу наличия помех каждый знак может быть неправильно принят с вероятностью 0,01. Найти вероятность того, что в принятом тексте, содержащем 1000 знаков, будет меньше 10 ошибок. 10. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва цепи в течение этого срока. p2 = p4 = p6 = 0.8 . p1 = p3 = p5 = p7 = 0.9 , 29 вариант 6. Из урны, содержащей 6 белых и 4 черных шара, вынимают без возвращения 4 шара. Найти вероятность того, что два шара белые и два – черные. 7. Из 1000 ламп 100 принадлежат 1-й партии, 250 – 2-й и остальные – 3-й партии. В 1-й партии 6 %, во 2-й – 5 %, в 3-й – 4 % бракованных ламп. Наудачу выбирается одна лампа. Найти вероятность того, что выбранная лампа бракованная. 8. В урне содержится 8 белых, 4 красных и 3 черных шара. Производится 5 извлечений с возвращением по одному шару. Найти вероятность того, что в результате извлечений появилось 3 белых шара и по одному остальных цветов. 9. Производятся независимые испытания, в каждом из которых событие А появляется с вероятностью 0,8. Найти вероятность того, что событие А произойдет в большинстве из 50 испытаний. 10. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва цепи в течение этого срока. p2 = p4 = p6 = 0.8 . p1 = p3 = p5 = p7 = 0.9 , 30 вариант 6. На отрезке [0,1] наудачу ставятся две точки. Найти вероятность события: расстояние между двумя точками меньше половины длины отрезка. 7. В магазин поступают одинаковые изделия с трех заводов, причем 1-й завод поставил 50 изделий, 2-й – 30, 3-й – 20 изделий. Среди изделий 1-го завода 70 % первосортных, а среди изделий 2-го – 80 %, 3-го – 90 % первосортных. Куплено одно изделие. Оно оказалось первосортным. Найти вероятность того, что это изделие выпущено 2-м заводом. 8. По каналу связи передается 20 знаков, каждый из которых, независимо от других, может быть искажен с вероятностью 0,01. Найти вероятность того, что будет искажено не более двух знаков. 9. Корректура в 500 страниц содержит 2000 опечаток. Найти наиболее вероятное число опечаток на одной странице и вероятность этого числа. 10. Даны вероятности безотказной работы в течение гарантийного срока отдельных элементов цепи pi . Отказы отдельных элементов цепи независимы. Определить вероятность обрыва цепи в течение этого срока. p2 = p4 = p6 = 0.8 . p1 = p3 = p5 = p7 = 0.9 ,