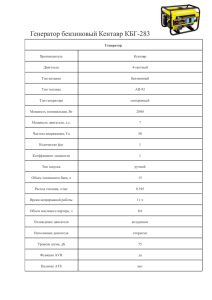
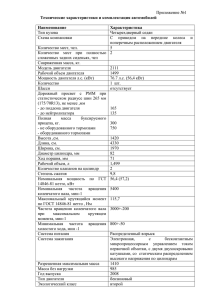
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ «МОГИЛЕВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ" Кафедра “Электропривод и АПУ” ЭП и АПУ ТАУ ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ПЕРЕДАТОЧНЫЕ ФУНКЦИИ АСИНХРОННЫХ ДВИГАТЕЛЕЙ Методические указания к лабораторно - практической работе 1 Двухфазный асинхронный двигатель Цель работы: составление уравнений и вывод передаточной функции двухфазного асинхронного двигателя 1 Краткие теоретические сведения Двухфазные асинхронные двигатели широко используются в автоматических системах. Наибольшее применение как исполнительные элементы они находят в маломощных следящих системах. Их достоинствами являются отсутствие щеток и коллектора, малый момент инерции ротора, простота и стабильность усиления сигнала с помощью усилителей переменного тока. Они не имеют коллектора и поэтому обладают высокой надежностью. В основном выпускаются двухфазные асинхронные двигатели двух типов: с полым немагнитным ротором из материала с хорошей электропроводностью (обычно из алюминия) и с ферромагнитным ротором, имеющим короткозамкнутую обмотку в виде беличьей клетки. Имея меньший к.п.д., двигатели первого типа отличаются малой инерцией ротора и лучшими регулировочными свойствами. Мощность указанных типов двигателей не превышает 100÷200 Вт. ∼Uу C2 iу C1 wу ωд ∼Uв Wв iв Рисунок 1 Схема двухфазного асинхронного двигателя На статоре двигателя располагаются обмотки возбуждения wв и управления wу, имеющие, как правило, одинаковое число витков. Оси обмоток сдвинуты в 90° пространстве на угол n (n – число пар полюсов одной обмотки). Обмотка возбуждения подключается к источнику переменного тока с фиксированным действующим напряжением Uв, а обмотка управления – к выходу усилителя переменного тока под напряжение Uу. Для нормальной работы двигателя фазы напряжений Uв и Uу должны быть сдвинуты на 90°. При 2 этом условии обмотки управления и возбуждения создают в статоре вращающееся магнитное поле, которое пересекая ротор, индуцирует в нем ток. Взаимодействие магнитного поля, наведенного током ротора, с вращающимся магнитным полем и создает вращающий момент двигателя. Конденсатор С1 включается в цепь возбуждения, когда обе обмотки питаются от однофазной сети, и служит для сдвига фаз между Uв и Uу на 90°. Конденсатор С2 может устанавливаться для компенсации индуктивного сопротивления в цепи обмотки управления, что позволяет понизить потери в выходном каскаде усилителя, обусловленные реактивной составляющей тока. Могут применяться и другие схемы включения обмоток. При одинаковых обмотках управления и возбуждения регулировочные характеристики двухфазного асинхронного двигателя без нагрузки имеют вид, представленный на рисунке 2. ω ω0 1 0.9 0.8 0.7 0.6 Мп 1 0.9 0.8 0.7 0.6 ω ω0 Мп 0.5 0.4 0.3 0.5 0.4 0.3 0.2 0.1 0.2 0.1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 Uу Uв Рисунок 2 Регулировочные характеристики двухфазного асинхронного двигателя Как видно из рисунка, максимальная скорость холостого Uу хода ω0 достигается при U =1. При этом вращающееся в магнитное поле является круговым. Дальнейшее увеличение этого соотношения ведет к появлению эллиптического вращающегося магнитного поля. Избыток величины магнитного поля по отношению к круговому создает лишь тормозящий 3 момент и скорость вращения холостого хода начинает падать. Механические характеристики нелинейные и зависят не только от собственных параметров асинхронного двигателя, но и от параметров выходного каскада усилителя а так же схемы включения обмоток. Поэтому механические характеристики, используемые в расчетах, должны соответствовать реальным условиям работы двигателя. Как правило, такие характеристики определяются экспериментально. В справочниках обычно приводятся технические данные двигателей для базовой схемы включения обмоток при управлении от источника с большой мощностью и малым внутренним сопротивлением. С помощью механических характеристик ω=f(Uу, М) (рисунок 3) можно найти управляющее напряжение при заданном статическом моменте на валу и напряжение трогания двигателя. ω ω0 1 ∆ω Uу4 0 ∆М Uу3 Uу2 Uу1 1 М* Рисунок 3 Механические характеристики асинхронного двигателя Механические характеристики реальных двухфазных асинхронных двигателей показаны на рисунке 3 сплошными линиями. Однако во многих случаях для предварительной оценки динамических свойств двигателя реальные механические характеристики заменяют прямыми (на рисунке пунктирные линии). Составим линейное уравнение динамики двигателя в отклонениях, проведя линеаризацию его механических характеристик. За входную величину примем напряжение на управляющей обмотке, а за выходную – угол поворота вала, 4 полагая момент сопротивления не зависящим от скорости вращения, что соответствует большинству применений двухфазных асинхронных двигателей. Механические характеристики двигателя следует линеаризовать в точке или области рабочего режима путем построения касательных к действительным характеристикам. Если по форме механические характеристики близки к линейным, то их можно заменить приближенными линейными характеристиками в виде параллельных прямых с наклоном, равным усредненному наклону прямых, соединяющих при заданных управляющих напряжениях точки пусковых моментов и холостого хода. Из дальнейшего рассмотрения исключим инерционность по цепи управления двигателя, так как эта величина практически очень мала. Проведя аналогию с двигателем постоянного тока при Lя=0, для асинхронного двигателя при постоянной амплитуде напряжения возбуждения и малых отклонениях переменных можно записать: 1 1 ωд=С Uу-С С Мд, е е м где ωд – скорость вращения двигателя; Uу – действующее значение напряжения на обмотке управления; Мд – момент двигателя; Се, См – постоянные двигателя, определяемые в области рабочего режима. При этом уравнение равновесия моментов имеет вид dωд Мд=JΣ dt +Мс. Решив уравнения электрического и механического равновесия совместно, получим уравнение двухфазного асинхронного двигателя в операторной форме записи (Тмр+1)Ωд(р)=kдUу(р)-kд вМс(р), 1 1 где kд=С ; kд в=С С - коэффициенты передачи двигателя е е м соответственно по управляющему и возмущающему воздействиям; JΣ Тм=С С - электромеханическая постоянная времени. е м Здесь JΣ=Jд+Jмех пр – суммарный момент инерции на валу двигателя; Jд – момент инерции ротора двигателя; Jмех пр – момент инерции 5 Постоянные Се и См могут быть найдены по механическим характеристикам при Мс=const и ωд=const: ∆Uу Се= ; ∆ωд ∆М . См= ∆Uу В случае приведения механических характеристик, как показано на рисунке 3: Uу Се= ; ωд0 Мп См=U , у где ωд0 и Мп – скорость при холостом ходе и пусковой момент при некотором напряжении управления Uу. При отсутствии механических характеристик постоянные двигателя можно определить приближенно по его номинальным данным. Если механическую характеристику двигателя на рабочем участке от номинальной скорости вращения ωд ном до ωд=0 при номинальном напряжении управления Uу ном считать линейной, то ∆Uу Мп-Мном Uу ном = М ⋅ ; Се= п ∆ωд ωд ном ∆М Мп =U , См= ∆Uу у ном Мном где ∆Uу=Uу ном-Uтр ном (здесь Uтр ном=Uу ном М - напряжение п трогания при номинальном моменте). В последнем случае коэффициенты уравнения двигателя запишутся как 1 Мп ωд ном kд=С =М -М ⋅U ; е п ном у ном ωд ном kд в=М -М ; п ном ωд ном Тм=JΣМ -М . п ном Передаточные функции двигателя на основании полученных соотношений имеют вид: Ωд(р) kд Wд(р)ωUд= U (р) =Т р+1; д м Ωд(р) -kд в Wд в(р)ωМс= М (р) =Т р+1. с м 6 Технические данные некоторых типов двухфазных асинхронных двигателей с полым ротором приведены в таблице 1. Пример Определить приближенную передаточную функцию двигателя АДП-262 по управляющему воздействию при Jмех пр=1,7⋅10-6 кг⋅м2. Для данного двигателя из таблицы 1 имеем следующие данные: Uу ном=125 В; ωд ном=194 рад/с; Мном=49⋅10-3 Н⋅м; Мп=88⋅10-3 Н⋅м; Jд=1,67⋅10-6 кг⋅м2. Определим суммарный момент инерции на валу двигателя: JΣ=Jмех пр+Jд=3,37⋅10-6 кг⋅м2. Используя номинальные данные двигателя, определим приближенные значения: Мп ωд ном 88⋅10-3 194 рад kд=М -М ⋅ U = ; -3 -3⋅125=3,5 п ном у ном 88⋅10 -49⋅10 В⋅с ωд ном 194 3 рад/с . kд в=М -М = -3 -3=4,97⋅10 п ном 88⋅10 -49⋅10 Н⋅м ωд ном 194 ≈0,017 с. Тэм=JΣМ -М =3,37⋅10-6 -3 п ном 88⋅10 -49⋅10-3 При найденных параметрах передаточные функции двигателя: Ωд(р) kд 3,5 Wд(р)ωUд= U (р) =Т р+1=0,017р+1; д м Ωд(р) -kд в -4,97⋅103 Wд в(р)ωМс= М (р) =Т р+1=0,017р+1. с м 2 Порядок выполнения работы 1) выбрать в таблице 1 двигатель и его параметры. 2) рассчитать неизвестные коэффициенты по данным из таблицы 1. 3) определить передаточную функцию двигателя. 7 3 Содержание отчета 1) цель работы; 2) схема подключения АД; 3) расчет коэффициентов; 4) вывод передаточной функции двигателя; 5) графики механических и регулировочных характеристик. Контрольные вопросы 8 Uмакс, В Iу, А Iу п, А Ру, Вт 28 16 26 38 42 53 65 105 23 45 88 0,25 0,3 0,5 1,38 49 ± 9,5 3,9 3,5 ± 0,35 6,6 11,5 ± 1,1 6,6 1,22 ± 0,12 14,4 2,4 ± 0,2 2,5 190 ± 15 6,5 36 ± 3,5 11,0 17 ± 1,5 110 120 110 165 270 120 240 240 125 120 160 0,18 0,18 0,22 0,37 0,51 1,2 0,65 0,9 0,58 0,65 0,73 0,42 0,56 1,7 0,92 1,25 0,6 0,75 1,15 8 9 12 38 42 55 68 76 26 25 35 - 10 ± 1,0 28 ± 2,0 3 ± 0,3 11 ± 1,0 5 ± 0,5 38 ± 3,5 21 ± 2,0 13 ± 1,3 5,9 9,8 14,2 39 44 56 73,5 98 49 93 196 9,8 13,7 16,7 58 64 69 83,4 118 88 167 343 0,29 0,29 0,29 1,18 1,18 2,0 2,0 4,3 0,8 1,3 2,2 № варианта rв, Ом 0,3 0,18 0,27 0,78 1,38 0,55 2,0 3,6 0,23 0,6 0,88 Jд⋅10-6 кг⋅м2 Св, мкФ 110 110 110 52 36 110 36 36 110 110 110 Мтр⋅10-3 Н⋅м Рв, Вт 5000 5000 7000 8800 8600 8600 8600 8600 2650 2650 2650 Мп⋅10-3 Н⋅м Iном в, А 4000 4000 6000 6000 6000 6000 6000 6000 1850 1950 2000 rу, Ом U в, В Обмотка управления n0, об/мин 2,4 400 4,1 8,9 24 500 27,8 35 500 46,4 70,5 9,5 50 19 41 Обмотка возбуждения nном, об/мин АДП-120 АДП-123 АДП-123Б АДП-263 АДП-263А АДП-363 АДП-363А АДП-563А АДП-262 АДП-362 АДП-562 Рном, Вт f, Гц Тип двигателя Мном⋅10-3 Н⋅м Таблица 1 Технические данные двухфазных асинхронных двигателей серии АДП 0,785 0,785 1,67 1,86 3,93 4,83 11,75 1,67 3,93 12,75 1 2 3 4 5 6 7 8 9 10 11 9 Трехфазный асинхронный двигатель Цель работы: составление уравнений и вывод передаточной функции трехфазного асинхронного двигателя 1 Краткие теоретические сведения Составим уравнение вращения ротора трехфазного электродвигателя d ωд Jд dt =Мд(t)-Mc(t). Момент движущих сил электродвигателя зависит от напряжения питания статора, угловой скорости вращения ротора ωд, как видно из рисунка 4, и характеризуется зависимостью Мд(t)=Мд(Uд, ωд), (кривая 1) а момент сопротивления изменяется по кривой 4 (рисунок 4) и определяется в виде Мс(t)=Мс(ωд). ω* 1.1 1 ωд0 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 4 1 2 A1 A A2 3 5 Б 0.1 0.2 0.3 0.4 Мд0=Мс0 0.8 0.9 1 Mд*,Мс* Рисунок 4 Характеристики двигательного момента и момента сопротивления трехфазного асинхронного электродвигателя Учитывая значительную нелинейность характеристик Мд(t) и Мс(t), линеаризуем их в относительно небольшом диапазоне изменения угловой скорости вращения электродвигателя ∆ωд (между точками А1 и А2). В точке А в установившемся режиме Мд0=Мс0. 10 Разлагая характеристики Мд(t) и Мс(t) в окрестности точки А в ряд Тейлора, получим 2 ∂М д 1 ∂ Мд ∆ωд + 2 ∆ω2д + ... Мд(t)=Мд0+ 1 ⋅ 2 ∂ω д 0 ∂ωд 0 2 1 ∂ Мд ∂М д ∆u 2 + ..., ... + ∆u + 2 1 ⋅ 2 ∂u 0 ∂u 0 где Мд0 – двигательный момент при ωд0 и U0; ∂М c 1 ∂ 2М c 2 ∆ ωд + Мс(t)=Мс0+ ∆ ω д + ... + 2 ∂ ω 1 ⋅ 2 ∂ ω д д 0 0 где Мс0 – момент сопротивления при ωд0. Возьмем первые два члена ряда, то есть ограничимся рассмотрением линейной части характеристик при Мд0=Мс0, и подставим полученные соотношения в уравнение движения: ∂М ∂М d∆ωд ∂М Jд dt =Мд0+ д ∆ωд + д ∆u -Мс0- c ∆ωд . ∂u 0 ∂ωд 0 ∂ωд 0 Учитывая равенство Мд0=Мс0 в точке А можно записать ∂М d∆ωд ∂М ∂М Jд dt + c − д ∆ωд = д ∆u . ∂u 0 ∂ωд 0 ∂ωд 0 Или, разделив все члены равенства на ωд0 d∆ωд ∂М ∂М ∆ωд u0 ∂М д ∆u ω Jд д0 + c − д = , ω ω ∂ u u ∂ ω ∂ ω 0 0 dt д0 д 0 д 0 д0 откуда получим dµ Тдdt+µ(t)=k⋅ρ(t), где Jд Тд= ; ∂М c ∂М д − ∂ω ∂ ω д 0 д 0 u0 ∂М д ωд0 ∂u 0 ; k= ∂М c ∂М д − ∂ω ∂ ω д 0 д 0 ∆ω µ= д ; ωд0 11 ∆u . u0 Применив к уравнению преобразование Лапласа, найдем передаточную функцию трехфазного асинхронного электродвигателя k µ(p) W(p)= =T p+1. ρ(p) д Относительно угла поворота якоря передаточную функцию асинхронного трехфазного электродвигателя можно записать в виде: k ϑд(p) W(p)= U(p) =р(T p+1). д ∂М В выбранной точке А наклон характеристики c ∂ωд 0 ∂М больше наклона характеристики д , поэтому в ∂ωд 0 k передаточных функциях апериодическое звено T p+1 является д устойчивым. Если вместо точка А рассмотреть точку Б (см. кривую 5 ∂М ∂М на рисунке 4), то c < д и передаточная функция ∂ωд 0 ∂ ωд 0 электродвигателя примет вид k µ(p) W(p)= =T p-1. ρ(p) д В этом случае апериодическое звено является неустойчивым; соответственно изменяется и передаточная функция относительно угла поворота ротора k ϑд(p) W(p)= U(p) =р(T p-1). д ρ= 2 Порядок выполнения работы 1) выбрать в таблице 2 двигатель и его параметры. 2) по данным из таблицы 2 построить механическую характеристику. 12 3) задавшись моментом сопротивления в виде α ω ω0 Мс(ω)=Мс0 e , рассчитать неизвестные коэффициенты передаточной функции. 3 Содержание отчета 1) 2) 3) 4) цель работы; расчет коэффициентов; вывод передаточной функции двигателя; график механической характеристики. Контрольные вопросы 13 Таблица 2 Технические данные трехфазных асинхронных двигателей Момент № варианта Тип Мощность Угловая Максимальный Критическое инерции скольжение ротора электродвигателя кВт скорость момент рад/с кг⋅м2 Н⋅м PНОМ sк Jд Ммакс ω0 4АА5ОА2У3 0,09 314,1 0,62 0,5 0,000025 1 4А80В2У3 2,2 314,1 19,1 0,38 0,0021 2 4А16ОМАУЗ 18,5 314,1 132 0,125 0,053 3 4А355М2У3 315 314,1 1960 0,075 3,2 4 4А71В4У3 0,75 157,1 11,4 0,4 0,0014 5 4А16ОS4У3 15,0 157,1 345 0,16 0,1 6 4А18ОМ6У3 18,5 104,5 362 0,135 0,22 7 4А315М6У3 132,0 104,5 2840 0,082 4,5 8 4А280S8У3 55,0 78,6 1436 0,08 3,2 9 4А355М10У3 110 62,8 3200 0,065 11,0 10 14