Физика

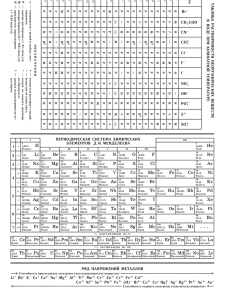
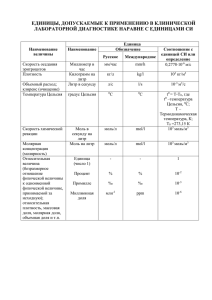
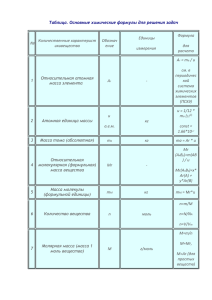
Задача 3
Дано:
Решение
R=0,8 м
Скорость это первая производная уравнения движения
ξ=At+Bt^3
V = ξ' = (At + Bt^3)’=A+3Bt^2
A=0,9 м/с
v = 9-3*0.1*3^2 = 6,3 м/с
B=-0,1 м/с^3
Ускорение это первая производная от скорости или вторая
производная от уравнения движения
t=3 с
a = v' = (3Bt^2)’=6Bt
a =-6*(-0,1)*3 = -1,8 м/с^2
V=?
a=?
ε=?
Угловое ускорение
ε = a/R
ε = -1,8 / 0,8 = - 2,25 рад/с^2
Ответ: V=6,3 м/с; a=-1,8 м/с^2; ε=-2,25 рад/с^2
Задача 6
Дано:
Решение
m1  60кг
m2  18т  60кг  17940кг
V1  480 м / с
  0,03
  30
S=?
Для определения скорости V2 воспользуемся законом сохранения
импульса
m1  V1  m2  V2
Спроектируем вектора импульсов на ось х
m1  V1  cos   m2  V2
V2 
m1  V1  cos  60  480  cos 30

 1,39 / c
m2
17940
По 2 закону Ньютона
Fтр  m2 a
Объект движется по горизонтальной поверхности
Fтр  т2 g
т2 g  m2 a
a  g
Определим расстояние
V22
V22
1,39 2
S


 0,03 м
2a 2g 2  0,03  9,81
Ответ: S=0,03 м
Задача 14
Дано:
Решение
m1  10г  0,01кг
Закон сохранения импульса
m 2  200г  0,2кг
k  25кН / м  25000 Н / м
m1  V1  m 2  V2
V  300 м / с
V2 
m1  V1 0,01  300

 15 м / с
m2
0,2
Кинетическая энергия затвора после выстрела
Δх=?
Ek 2 
m2  V22 m2  m12  V12 m12  V12


2
2  m2
2  m22
Эта энергия идет на деформацию пружины. Найдем энергию
деформированной пружины
1
k (x) 2
2
(m  V ) 2
1
k (x) 2  1 1
2
2  m2
W
Откуда искомая величина
x 
(m1  V ) 2

k  m2
Ответ: Δх=4,2 см
0,01 300
 0,042 м  4,2см
25000  0,2
Задача 17
Дано:
Решение
R=40см=0,4м
Запишем закон сохранения момента импульса относительно оси
вращения платформы
m=4 кг
J=8 кг*м^2
α=30°
F=500Н
t=1,5c
J 01  J 02
J0 – момент инерции колеса
Считаем, что после поворота колеса, его момент инерции
относительно оси вощения скамьи стал равным 0. Следовательно,
угловая скорость платформы после поворота
 2  1
n2=?
J0
J
Найдем угловую скорость колеса
Момент силы натяжения шнура
M=FR или M  J 0 
Для колеса J 0 

1
 FR 
mR 2 4  0,4 2

 0,32кг  м 2
2
2
mR 2 1
FRt  2 F  t  2

 1 


2
t
mRK
mR 2
t
500  1,5  1

 937,5c 1
4  0,4
0,32
 2  937,5 
 37,5c 1
8

37,5
 2  2n2  n2  2 
 5,97об / с
2 2  3,14
Ответ: n2=5,97 об/с
Задача 25
Дано
Решение
m  1,3кг
Механическая энергия это сумма кинетической и потенциальной
энергий. Кинетическая энергия это сумма кинетической энергии
l  1м
U  7м / с
mU 2
поступательного движения
и кинетической энергии
2
n  5c 1
вращательного движения
Е=?
mU 2 J 2
T

2
2
h  1,6 м
J 2
2
Момент инерции биты относительно оси вращения
J
1
1
ml 2   1,3  12  0,108кг  м 2
12
12
Угловая частота вращения
  2n  2  3,14  5  31,416 рад / с
Тогда полная кинетическая энергия
T
1,3  7 2 0,108  31,4162

 85,146 Дж
2
2
Потенциальная энергия тела равна
En  mgh  1,3  9,807  1,6  20,399 Дж
E  T  Eп  85,146  20,399  105,545 Дж
Ответ: Е=105,545 Дж
Задача 28
Дано:
Решение
l  1,5 м
  2,5
m1  1кг
Положение центра масс:
r1  1м
L  (m1  m 2 )  r1 m1  r2 m 2
r1  m1  r2  m 2 1  1  1,5  2

 1,333 м
m1  m 2
1 2
L
m 2  2кг


4
Оно равно расстоянию «а» от центра масс до точки подвеса.
Момент инерции:
l ?
J  m1  r12  m2  r22  1  12  2  1,5 2  5,5кг  м 2
Ek  ?
Полная масса:
E p ?
t ?
m  m1  m2  3кг
Приведённая длина:
l
J
5,5

 1,375 м
ma 3  1,333
Период колебаний маятника:
l
1,375
 2  3,14 
 2,35c
g
9,8
t  2
Уравнение колебаний:
 (t )  sin( 2t t )  0,0218  sin( 2,67t )
a
2
Скорость (угловая):

d
 0,0582 cos( 2,67t ) c 1
dt
Полная кинетическая энергия:
E k  0,5  J   2  0,5  5,5  0,0582 2  0,00931 Дж






  
 
 3,14 
1
  0,0582  cos
  0,0412 c
4
4


 3,14 
1
  0,0582 cos
  0,0412 c
4
 4 


E k      0,5  5,5  0,0412 2  0,00467 Дж
4

Потенциальная:




E p      E k  E k      0,00931  0,00467  0,00464 Дж
4
4


 E



E p     k  E k   
4 2
4


Для t:
2,67t 

4
t 
3,14 / 4
 0,294c
2,67
Или: t = T/8 = 2,35/8 = 0,29375 c = 0,294 c
Ответ: l=1,375м; Ек=0,00467 Дж; Еп=0,00464 Дж; t=0,294с
Задача 31
Дано:
Решение
V1  10 л  0,01м 3
Т.к. Т=const, то воспользуемся законом Бойля-Мариотта
P1  1,5МПа  1,5  10 6 Па
V2  22 л  0,022 м 2
P2  0,6 МПа  0,6  10 6 Па
Т  const
 в р 4,14  10  21 Дж
P1'
P2'
n1
n2
m1
m2
P1V1  P ' (V1  V 2 )  P' 
P1V1
V1  V 2
P '1 
1,5  10 6  0,01
 470000 Па  0,47 МПа
0,01  0,022
P' 2 
0,6  10 6  0,022
 410000 Па  0б 41МПа
0,01  0,022
Т.к. гелий одноатомный газ, то число степеней свободы у него 3,
следовательно, средняя кинетическая энергия вращательного движения
 в р  
i 3
33
kT 
kT  0 Дж
2
2
Кислород двухатомный i=5
 вр  
 вр  2
i 3
4,14 10 21  2
kT  T 

 300 К
2
k (i  3)
2 1,38 10  23
Найдем концентрацию молекул кислорода
P'1  n1kT  n1 
P'1
0,47 106

 1,14 1026 шт
23
kT 1,38 10  300
Найдем массу молекул кислорода
n1 
m1
m0
no1 
n1 
M1
32  10 3

 5,3  10 26 кг
23
N A 6,022  10
m1
 m1  n1mo1  1,14  10 26  5,3  10 26  5,96кг
m0
Найдем концентрацию гелия
P'2  n2 kT  n2 
P' 2
0,41106

 0,99 1026 шт
23
kT 1,38 10  300
Найдем массу молекул гелия
n2 
m2
 m2  n2 mo 2
m0
M2
4 10  3
m02 

 0,66 10  26 кг
23
N A 0,022 10
m2  0,99 10 26  0,66 10  26  0,65кг
Ответ:
P1'  0,47МПа; P2'  0,41МПа; n1  1,14 1026 шт;
n2  0,99 1026 шт; m1  5,96кг ; m2 0,65кг
Задача 39
Дано:
Решение
S=1 га= 10^4 м^2
Для определения градиента плотности углекислого газа
используем закон Фика
t=2 ч= 7,2*10^3 c
d
dx
m=6 кг
jm   D
D=0,04 см^2/c
d
j
 m
dx  D
= 4*10^(-6) м^2/с
tв=17°С=290 К
Плотность потока массы
m
6

 2,07  10 6
St 10000  290
d 2,07  10 6

 0,52
dx
4  10 6
jm 
d
?
dx
Dr
?
D
Влияние среды на интенсивность диффузии определяется
отношением коэффициентов диффузии, т. к. подразумевается
соотношение диффундирующих масс, имевших место при
одинаковых числовых значениях

, S , t . Следовательно,
х
ответом на второй вопрос задачи будет числовое значение
отношения
Dr
, где Dr — коэффициент диффузии углекислого
D
газа через газовую среду (воздух). Известно, что
1
Dr  l   (1)
3
где l  - средняя длина свободного пробега молекулы в
газовой среде (воздухе);
  - средняя арифметическая скорость молекулы CO2 .
0ценим значения l  ,   для случая диффузии углекислого газа
через воздух при температуре, равной средней
температур почвы
l  
1
(2)
2d 2 n
где d - эффективный диаметр молекулы диффундирующего
газа;
n - концентрация молекул газа, являющегося средой диффузии.
  
8 RT

(3)
где R - универсальная газовая постоянная;
Подставим 3 и 2 в 1, выразим отношение
Dr
2 RT

(4)
D 3Dd 2 n  3 
Выразим концентрацию молекул воздуха
n
N vN

(5)
V
V
где v - количество вещества;
Na - постоянная Авогадро;
V - объем.
По уравнению состояния идеального газа
pV  vRT
где р — давление воздуха, имеем
v
pV
(6)
RT
Подставив последовательно 6 в 5 и затем в 4, получим
Dr
2 R 3T 3
(7)

D 3Dd 2 pN A  3 
Учитывая, что p  10 3 Па (атмосферное давление), R=8,31
Дж/(моль*К) , Na=6,02*10^23 1/моль, d=3.5*10^(-10)м, μ=44*10^)-3)
кг/моль (молярная масса СО2), T  273  t n  290 K , сделаем
подстановку в 7 и вычисление:
2 8,313  290 3
Dr

 2,64
D 3  3,5  10 6 (3,5  10 10 ) 2  10 5  6,02  10 23 3,14 3  0,044
d
 0,52
dx
Ответ:
Dr
 2,62
D
Задача 43
Дано:
Решение
m1  5г  0,005кг
Показатель адиабаты это отношение молярных теплоемкостей
m2  2г  0,002кг

?
1

?
2
 
С p
C V
C V 
iR
молярная теплоемкость газа при постоянном объеме
2
С p 
(i  2) R
молярная теплоемкость газа при постоянном
2
давлении
Для гелия число степеней свободы i=3, для водорода i=5
Для молярной теплоемкости смеси при постоянном объеме можно
записать
( 1   2 )  С V   1C V 1   2 C V 2

(
m
M
m1 m2
m
m

)  С V  1 C V 1  2 C V 2
M1 M 2
M1
M2
Отсюда молярная теплоемкость смеси при постоянном объеме
C V
m1 i1 R m2 i2 R

M1 2 M 2 2

m1 m2

M1 M 2
Для молярной теплоемкости смеси при постоянном давлении
получим
М 1  4  10 3 кг / моль
М 2  2  10 3 кг / моль
0,005 (3  2)8,31 0,002 (5  2)  8,31

3
Дж
2
2
4

10
2  10 3
Сp 
 74,47
0,005
0,002
моль  К

3
3
4  10
2  10
0,005 3  8,31 0,002 5  8,31

3
Дж
2
2
2  10 3
СU  4  10
 16,17
0,005
0,002
моль  К

3
3
4  10
2  10
24,47
 
 1,51
16,17
(3  2)8,31
Дж
 20,78
2
моль  К
3  8,31
Дж
С v1 
 12,47
2
моль  К
(5  2)8,31
Дж
С p2 
 29,1
2
моль  К
5  8,31
Дж
Сv2 
 20,78
2
моль  К
20,78
1 
 1,67
12,47
29,1
2 
 1,4
20,78
 1,51

 0,9
 1 1,67
С p1 
 1,51

 1,1
 2 1,4
Ответ:


 0,9;
 1,1
1
2
Задача 46
Дано:
Решение
m  200 г  0,2кг
Формула КПД тепловой машины
Q2  14кДж  14000 Дж
A  6кДж  6000 Дж
Т 2  280 К
Q1  Q2
A

Q1
Q1

A  Q1  Q2
Q1  A  Q2  6000  14000  20000 Дж
Т1  ?
V1
?
V2
КПД можно выразить как

T1  T2
T
1 2
T1
T1
T2
T  Q1
280  20000
 2

 400 K
A Q1  A Q1  A 20000  6000
1
Q1
Q1
При изотермическом расширении работа численно равна
площади фигуры под изотермой
T1 
T2

1 
T2
A
V
V
m
AM
RT  ln 2  ln 2 
M
V1
V1 RTm

M O2   44  10 3 кг / моль
ln
V2 6  10 3  44  10 3
V

 0,57  2  e 0,57  1,77
V1
8,31  280  0,2
V1
Ответ: Т 1  400 К ;
V1
 1,77
V2
Задача 54
Дано:
Решение:
d=1мм=10^(-3)м
h=20мм=20*10^(-3)м
Поверхность жидкости в капилре принимает вогнутую
сферическую фрму, значит, внутреннее давление жидкости в
капиляре будет меньше, чем вне капиляра, на величину
избыточного давления под сферической поверхностью
α=?
p 
2
R
Жидкость в капиляре поднимается на такую высоту h, при
которой оказываемое ею давление станет равным
избыточному
h   g 
h
2
R
2
R   g
ρ=1260 кг/м^3 – плотность глицирина
Так как угол между радиусом r и R и краевой угол θ равны
между собой
r
cos 
2  cos 
h
rg
R
При условии полного смачивания θ=0° полуаем
h
2
rg
Отсюда коффициент поверхностного натяжения жидкости
hr    g
2
d  2r


h  d    g 20  10 3  1  10 3  1260  9,81

 0,062 Н / м
4
4
Ответ: α=0062 Н/м