6

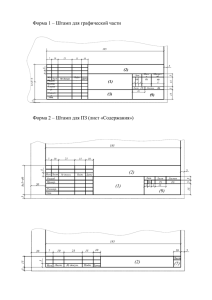
Практическая работа 6. Выбор типа регулятора и расчёт его настроек.
1.
1.1
1.2
Цель рабы:
Научиться выбирать тип регулятора для САУ;
Научиться вычислять настройки выбранного регулятора
2.
Теоретическая информация
Автоматическим
регулятором называется
устройство,
обеспечивающее в системах автоматического регулирования (АСР)
поддержание технологической величины объекта, характеризующей
протекание в нем процесса около заданного значения путем воздействия на
объект. Заданное значение может иметь постоянную величину (в системах
стабилизации) или изменяться по определенной программе (в системах
программного регулирования).
Структурная схема регулятора может быть представлена как
совокупность двух элементов: элемента сравнения 1 и элемента 2,
формирующего алгоритм (закон) регулирования.
Рисунок 1 – Классическая схема автоматического регулятора
На элемент сравнения 1 поступают два сигнала х и хзд,
пропорциональные, соответственно, текущему и заданному значениям
регулируемой
величины.
Сигнал х формируется
измерительным
преобразователем, а сигнал хзд – задатчиком или программным устройством.
Сигнал рассогласования ε = хзд – х поступает в элемент 2, который
вырабатывает
выходной
сигнал
регулятора,
направляемый
на
исполнительное устройство.
Регуляторы могут быть с прямой и обратной характеристикой. Если с
увеличением х относительно хзд выходная величина у увеличивается, то
регулятор имеет прямую характеристику, а если уменьшается, то –
обратную характеристику. Переход с прямой характеристики на обратную
и наоборот в регуляторах осуществляют при помощи специального
переключателя. Отрицательную обратную связь в замкнутом контуре АСР
формируют посредством применения регуляторов с прямой или обратной
характеристикой.
Законом регулирования называется зависимость между изменением
выходной
величины
регулятора у и
рассогласованием
текущего х и хзд значений
регулируемой
величины.
Все
законы
регулирования подразделяются на простейшие: пропорциональный (П),
интегральный
(И),
дифференциальный
(Д)
и
промышленные:
пропорционально-интегральный (ПИ), пропорционально-дифференциальный
(ПД), пропорционально-интегрально-дифференциальный (ПИД).
3. Пример.
Расчёт АСР ______________________________(см. Приложение А).
1.1 Построение кривой разгона объекта управления и определение
его динамических параметров.
1.1.1. Передаточная функция объекта управления (см. Приложение А):
W ( p) 
(1)
1.1.2. Характеристическое уравнение динамики ОР:
(2)
определим его корни:
р1, 2 
p1 
 в  в 2  4ас
2а
p2 
а1  р1
а2  р2
следовательно:
а1 
а2 
1.1.3. Из передаточной функции определяем коэффициент передачи
объекта:
м3
K 0 =[
ч ]
% ходаРО
1.1.4. Обозначим:
x(t)= Х вых
y(t)= Х в х
1.1.5. Переходную функцию математически можно записать формулой,
которая является решением дифференциального уравнения второго порядка:
Х вых  А1е  а1t  А2 е  а2t  K 0 Х вх
(3)
Определим А1 по формуле:
А1  K 0 Х вх
а2
а1  а2
(4)
Определим А2 по формуле:
А2   K 0 Х вх
а1
а1  а2
(5)
Лист
Изм. Лист
№ докум.
Подпись Дата
Подстави в в формулу (3), значения из формул (4) и (5), получим:
Х вых = K 0 Х вх (1+
а2
а1
е  а1t е  а2t )
а1  а2
а1  а 2
(6)
а2
=
а1  а 2
а1
=
а1  а2
Перепишем формулу (6), подставив свои значения:
Х вых =
(7)
1.1.6. Для расчёта параметров кривой объекта управления, задаём
значения времени от нуля до бесконечности, строим кривую разгона,
используя программу (рисунок 1).
1.1.7. Данные расчётов сводим в таблицу 1.
Таблица 1-Результаты вычислений.
t
е  a1t
е  a2t
Х вых
0
1
2
5
10
25
50
Кривая объекта управления, построенная по результатам вычислений из
таблицы 1 представлена на рисунке 1.
Лист
Изм. Лист
№ докум.
Подпись Дата
Рисунок 1-Кривая разгона с динамическими характеристиками объекта
управления
1.1.8. Находим координаты точки перегиба из условия, Х вых (t ) = 0, при
t=tп.
Х вых  А1е  а1t  А2 е  а2t  K 0 Х вх

X вых (t ) =  а1 А1е  а1t  а2 А2 е  а2t

2
2
Х вых (t ) =  а1 А1е  а1t  а 2 А2 е  а2t
 м3

ч

 , получаем формулу:
При условии, что Х вых =0
 % ходаРО 


2
2
 а1t
 а2t
а1 А1е
 - а2 А2 е
(8)
подставим в данное выражение значения, получим:
K 0 Х вх
а2
а1
2
2
а1 е  а1t = K 0 Х вх
а 2 е  а2t
а1  а2
а1  а 2
а1 е  а1t = а 2 е  а2t
2
2
а1е  а1t = а2 е  а2t
Разделив обе части уравнения на а2 , получим:
е  а2t =
а1  а1t
е
а2
 а2 t  ln
a1
 a1t
a2
 а2 t п  ln
a1
 a1t п
a2
Примем t= t n , тогда:
Время, соответствующее точке перегиба, находится по формуле:
tn 
ln a1  ln a2
a1  a2
(9)
подставив значения, получим:
tn 
Лист
Изм. Лист
№ докум.
Подпись Дата
tn =
С учётом того, что транспортное запаздывание равно:  тр  с. время,
соответствующее точке перегиба равно:
t n1 =
1.1.9. Для определения времени запаздывания  е , используем
зависимость:
X (t n )
 tg  X ' (t n )
tn   с
 с  tn 
X (t n )
X ' (t n )
(10)
 м3

ч


Из рисунка 1 находим, что X вых (t n ) =
 % ходаРО 


Производная от X вых (tn ) , будет иметь вид:

X вых (t п )  K 0 Х вх (- а1
а2
а1
е  а1t + а2
е  а2t )
а1  а 2
а1  а 2
(11)
Подставив значения, получим:

м3
X вых = [
ч
]
% ходаРО
Подставим числовые значения в формулу для расчёта (10):
 с=
с =
1.1.10. С учётом транспортного запаздывания полное время
запаздывания будет равно:
 з   с   тр
(12)
з =
з =
1.1.11. Постоянную времени объекта найдём по формуле:
Т 0  t n1  T1   з
(13)
T1 определим из подобия двух треугольников по графику кривой разгона
(рисунок 1):
Лист
Изм. Лист
№ докум.
Подпись Дата
X вых1 (t п ) t n1   з

X вых 2
Т1
где
Х
= К 0  X вых1 (t п )
вых2
выразим из этого выражения T1 :
T1 =
X вых2 (t n1   з )
X вых1 (t п )
T1 =
T1 =
Подставим значения в формулу (13) для нахождения Т 0 :
Т0 =
Т0 =
2.2. Выбор закона регулирования, определение параметров
настройки регулятора.
2.2.1. Динамические параметры объекта управления.
2.2.1.1. Максимальный, в условиях эксплуатации, коэффициент
передачи объекта управления:
м3
K0 =[
ч ]
% ходаРО
2.2.1.2. Постоянная времени объекта управления:
Т0 =
2.2.1.3. Запаздывание:
з =
2.2.1.4. Величина максимально возможного возмущения по нагрузке в
процессе эксплуатации объекта управления (см.Приложение А):
ув  %
2.2.2. Основные показатели качества переходного процесса.
2.2.2.1. Максимально допустимое динамическое отклонение
регулируемой величины (см.Приложение А):
Хд  м
3
ч
Лист
Изм. Лист
№ докум.
Подпись Дата
2.2.2.2. Максимально допустимое статическое отклонение регулируемой
величины (см.Приложение А):
Х ст  м
3
ч
2.2.2.3. Допустимое время регулирования (см.Приложение А):
t рег  с.
2.2.3. Порядок выбора закона регулирования.
2.2.3.1. Величину, обратную относительному времени запаздывания
находим по формуле:
1 з

z0 Т 0
(14)
подставив значения, получим:
2.2.3.2. Допустимое относительное время регулирования находим по
формуле:
t рег
з

(15)
доп
2.2.3.3. Допустимый динамический коэффициент регулирования
находим по формуле:
Rд 
Xд
=
К 0 ув
(16)
2.2.3.4. Допустимое остаточное отклонение регулируемой величины
находим по формуле:
( уост ) доп 
Х ст
К 0 ув
(17)
подставив в эту формулу значения, получим:
( уост ) доп 
выразим эту величину в процентах:
( уост ) доп  %
2.2.3.5. Большинство автоматизированных металлургических процессов
в САУ с регулятором непрерывного действия протекают успешно, если в
системе имеет место один из трёх типовых процессов регулирования:

Апериодический

С 20% перерегулированием

С min интегральной квадратичной ошибкой
По значению  з Т выбираем тип регулятора.
0
Лист
Изм. Лист
№ докум.
Подпись Дата
Значению
з
= соответсвует непрерывный тип регулятора. Так как показатель
Т0
колебательности М принадлежит промежутку 1<M<1,2, то выбираем
апериодический процесс (если показатель колебательности М принадлежит
промежутку 1,4<M<1,8, то выбираем процесс с 20% перерегулированием).
Пользуясь графиком зависимости Rд от  з Т (рисунок 2) при выбранном
0
оптимальном процессе, определяем, что Rд =, при
1
=
z0
могут обеспечить
??? – регуляторы (выберите, какие регуляторы подойдут).
Рисунок 2 - Динамический коэффициент регулирования на статических
объектах при различных процессах: а) апериодическом; б) с 20%-м
перерегулированием; в) с минимальной площадью квадратичного
отклонения; 1-И-регулятор; 2-П-регулятор; 3-ПИ-регулятор; 4-ПИДрегулятор.
Выбираю П – регулятор. По графику зависимости уост  f ( z 0 ) (рисунок
3) определим остаточное отклонение при установке П- регулятора.
Лист
Изм. Лист
№ докум.
Подпись Дата
Рисунок 3 - Статическая ошибка в АСР со статическим объектом и
непрерывным регулятором: 1) апериодическом; 2) с 20%-м
перерегулированием; 3) с минимальной площадью квадратичного
отклонения.
уост =
Выразим из формулы (17) Х ст :
Х ст = у ост К 0 ув
Подставив в эту формулу значение у ост , определённое по графику:
Х ст =
Х ст = ( м ч )
3
Так как допустимое значение Х ст < м ч , то П – регулятор не
может/может быть применён.
3
Выбираю ПИ – регулятор (если нужно).
Определим, каким будет время регулирования для ПИ – регулятора. Оно
должно быть меньше (t рег ) доп :
(t рег ) доп = с.
Для определения t р воспользуемся графиком зависимости
t рег

  f( t)
(рисунок 4) для процесса с 20% перерегулированием:
Рисунок 4 - Время регулирования на статических объектах при
процессах:
Лист
Изм. Лист
№ докум.
Подпись Дата
а) апериодическом; б) с 20%-м перерегулированием; в) с минимальной
площадью квадратичного отклонения; 1-И-регулятор; 2-П-регулятор; 3-ПИрегулятор; 4-ПИД-регулятор.
t рег 
t рег

* з
t рег 
t рег 
t рег ???(t рег )доп (меньше или больше) следовательно, апериодический
процесс не может/может быть реализован в САУ ПИ – регулятором.
2.2.4. Приближенное определение настроек регулятора произведём по
следующим формулам
2.2.4.1. Коэффициент усиления регулятора найдём по формуле:
Кр 
0,7
(18)

К0 * з
Т0
Кр =
% ходаИМ
м3
ч
2.2.4.2. Время удвоения (изодрома) найдём по формуле:
Т и  0,7Т 0
(19)
Т и  с.
Лист
Изм. Лист
№ докум.
Подпись Дата
4.
Ход работы:
4.1. изучите теоретическую часть методических указаний к
практической работе;
4.2 выполните задание к практической работе согласно своему варианту
(варианты представлены в Приложении А):
4.3 ответьте на контрольные вопросы;
4.4 сделайте вывод по работе;
4.5 приготовитесь к защите работы по темам в конспекте:
«Автоматические законы регулирования», «Типовые динамические звенья»
5.
Контрольные вопросы:
5.1 Что такое автоматический регулятор?
5.2 Что такое автоматический закон регулирования?
5.3 Какие два основные виды автоматического регулятора бывают?
Приложение А
Вариант 1: Расчёт АСР расхода кислорода на продувку конвертора
Вариант 2: Расчёт АСР расхода природного газа для отопления
секционной печи
Вариант
№
1
2
Передаточная
функция
ув, %
 1,5 p
0,5e
W ( p) 
1,9 p 2  3,05 p  1
 30 p
2,5e
60 p 2  100 p  1
W ( p) 
Хст <,
м3/ч
0,4
tрег, с
М
12
Хд <,
м3/ч
2,5
500
1,1
15
15
0,8
800
1,6