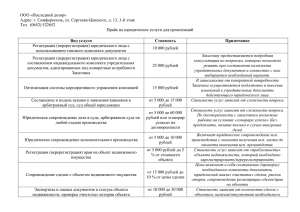
Контрольно-оценочные средства для проведения текущего контроля по ЕН.04 Математические методы в программировании (3 курс, 5 семестр 2018-2019 уч. г.) ПЗ №1 Имеются три поставщика однородного товара с объемами поставок: а1=100т, а2= 200т, а3=100т, и четыре потребителя с объемами потребления b1=80т,b2=120т,b3=150т,b4=50т. Определить оптимальное решение перевозок, обеспечивающее минимальные транспортные затраты. ПЗ №2 Фирма производит платья и костюмы, реализация которых зависит от состояния погоды. Затраты фирмы в течение апреля-мая на единицу продукции составят: платья – 5 ден. ед., костюмы – 25 ден. ед. Цена реализации составит 10 ден. ед. и 40 ден. ед. соответственно. По данным наблюдений за несколько предыдущих лет фирма может реализовать в условиях теплой погоды 1 220 платьев и 550 костюмов, при прохладной погоде – 410 платьев и 930 костюмов. В связи с возможными изменениями погоды определить стратегию фирмы в выпуске продукции, обеспечивающую ей максимальный доход. Задачу решить графическим методом и с использованием критерия Гурвица, приняв степень оптимизма 0,4 ПЗ №3 Имеется два способа производства некоторого продукта. Издержки производства при каждом способе зависят от произведенных x1 и у2 следующим образом: g(x1)= 9x1 + x12, g(x2)=6x2 + x22 . За месяц необходимо произвести 3×50 единиц продукции, распределив ее между двумя способами так, чтобы минимизировать общие издержки. ПЗ №4 Для двух предприятий выделено единиц средств. Как распределить все средства в течение 4 лет, чтобы доход был наибольшим, если известно, что доход от единиц средств, вложенных в первое предприятие, равен , а доход от единиц средств, вложенных во второе предприятие, равен . Остаток средств к концу года составляет для первого предприятия и для второго предприятия. Задачу решить методом динамического программирования. ПЗ №5 Решить задачу о коммивояжёре, т.е. найти гамильтонов цикл минимальной стоимости. Выберем один из точных алгоритмов, а именно, венгерский алгоритм. Условие: Значения элементов матрицы расстояний: a(1.1)= ∞ ; a(2.1)=53; a(3.1)=32; a(4.1)=21; a(5.1)=22 a(1.2)=25; a(2.2)= ∞; a(3.2)=72; a(4.2)=45; a(5.2)=43 a(1.3)=15; a(2.3)=34; a(3.3)= ∞; a(4.3)=29; a(5.3)=34 a(1.4)=18; a(2.4)=36; a(3.4)=18; a(4.4)= ∞; a(5.4)=46 a(1.5)=46; a(2.5)=75; a(3.5)=24; a(4.5)= 17; a(5.5)= ∞ ПЗ №6 Пусть для некоторого комплекса работ установлены оценки для каждой работы на уровне нормативных продолжительностей и срочного режима, а также даны стоимости. Информация представлена в таблице. Таблица 1. Нормативный режим Продолжительность, дни Срочный режим Стоимость, м/р Продолжительность, дни Стоимость, м/р (1,2) 3 6 2 11 (1,3) 5 8 3 12 (1,4) 4 7 8 9 (2,5) 10 25 8 30 (3,5) 8 20 6 24 (3,6) 15 26 12 30 (4,6) 13 24 10 30 (5,7) 3 15 6 25 (6,7) 4 10 3 15 Построить график данного комплекса работ. Требуется рассчитать: временные характеристики сетевого графика при нормальном режиме работ; найти критический путь; полные резервы времени; временные характеристики сетевого графика при срочном режиме работ; найти критический путь; полные резервы времени; определить стоимость работ. ПЗ №7 ПЗ №8 Пусть задан связный неориентированный граф G=(V,E)G=(V,E) с весами рёбер f(e)f(e) . Подграф, являющийся деревом и проходящий через все вершины GG , называется основным деревом. Остовное дерево называется минимальным, если суммарный вес его рёбер является минимальным среди всех остовных деревьев. ПЗ №9 В цехе предприятия решено установить дополнительное оборудование, для размещения которого выделено площади. На приобретение оборудования предприятие может израсходовать 10 тыс. руб., при этом оно может купить оборудование двух видов. Комплект оборудования I вида стоит 1000 руб., а II вида – 3000 руб. Приобретение одного комплекта оборудования I вида позволяет увеличить выпуск продукции в смену на 2 ед., а одного комплекта оборудования II вида – на 4 ед. Зная что для установки одного комплекта оборудования I вида требуется 2 м2 площади, а оборудования II вида – 1 м2 площади определить такой набор дополнительного оборудования, которых дает возможность максимально увеличить выпуск продукции ПЗ №10 На приобретение дополнительного оборудования фирма выделила 10 усл. ед., при этом она может купить оборудование двух видов. Приобретение 1–го комплекта оборудования 1–го вида стоит 1,0 усл. ед., 2–го вида — 3 усл. ед. Приобретение одного комплекта оборудования 1–го вида позволяет увеличить выпуск продукции в смену на 2 шт., а одного комплекта оборудования 2–го вида — на 4 шт. Зная, что для установки одного комплекта оборудования 1–го вида требуется 2м2 площади, а для оборудования 2–го вида — 1м2 площади, определить такой набор дополнительного оборудования, который дает возможность максимально увеличить выпуск продукции. ПЗ №11 Стоимость доставки единицы продукции от поставщика к потребителю располагается в правом нижнем углу ячейки. Потребитель Поставщик Запас B1 B2 B3 A1 5 3 1 10 A2 3 2 4 20 A3 4 1 2 30 Потребность 15 20 25 Требуется составить план перевозок, при котором общая стоимость доставки продукции будет наименьшей. ПЗ №12 1. Составить допустимый план транспортной задачи, используя метод минимальной стоимости или Мюллера-Мербаха для построения базисного плана с ограничением пропускной способности. 2. Найти оптимальный план транспортной задачи, используя метод потенциалов. Построенный допустимый и оптимальный план должен удовлетворять условиям постановки транспортной задачи. a. b. c. d. 0<=xij<=dij e. Целевая функция задачи 3. Рассчитать целевые функции каждого базисного плана перевозок. 4. Найти экономический эффект от оптимизации. Экономический эффект от оптимизации рассчитывается как разность между целевыми функциями базисного и оптимального планов. 5. Рассчитать матрицу показателей характеристик оптимального плана перевозок транспортной задачи. Характеристики клеток рассчитываются по формуле: Dij = cij – (vj – Uj) 6. Показать варианты альтернативных решений при одной и той же целевой функции и при минимальных от нее отклонениях ПЗ №13 Определим максимальное значение целевой функции F(X) = 3x1 +5x2 +4x3 при следующих условиях-ограничений. 0.1x1 + 0.2x2 + 0.4x3≤1100 0.05x1 + 0.02x2 + 0.02x3≤120 3x1 + x2 + 2x3≤8000 ПЗ №14 Матрица тарифов (здесь количество поставщиков равно 4, количество магазинов равно 6): 1 2 3 4 5 6 Запасы 1 3 20 8 13 4 100 80 2 4 4 18 14 3 0 60 3 10 4 18 8 6 0 30 4 7 19 17 10 1 100 60 30 40 50 70 30 Потребности 10 ПЗ №15 Компания изготавливает два вида продукции – П1 и П2. Для производства продукции используются два вида сырья – С1 и С2. Оптовые цены единицы продукции равна: 5 д.е. для П1 и 4 д.е. для П2. Расход сырья на единицу продукции вида П1 и вида П2 дан в таблице. Таблица - Расход сырья на производство продукции Сырье Расход сырья на 1 ед. продукции Максимальный запас сырья, ед. П1 П2 М1 6 4 24 М2 1 2 6 Установлены ограничения на спрос продукции: ежедневный объем производства продукции П2 не должен превышать ежедневный объем производства продукции П1 не более чем на 1 тонну; максимальный ежедневный объем производства П2 не должен превышать 2 т. Требуется определить: Какое количество продукции каждого вида должно производить предприятие, чтобы доход от реализации продукции был максимальным? 1. Сформулировать математическую модель задачи линейного программирования. 2. Решить задачу линейного программирования графическим способом (для двух переменных).