Вариант № 2794201 1. B 1 № 25005. Шоколадка стоит 40 рублей

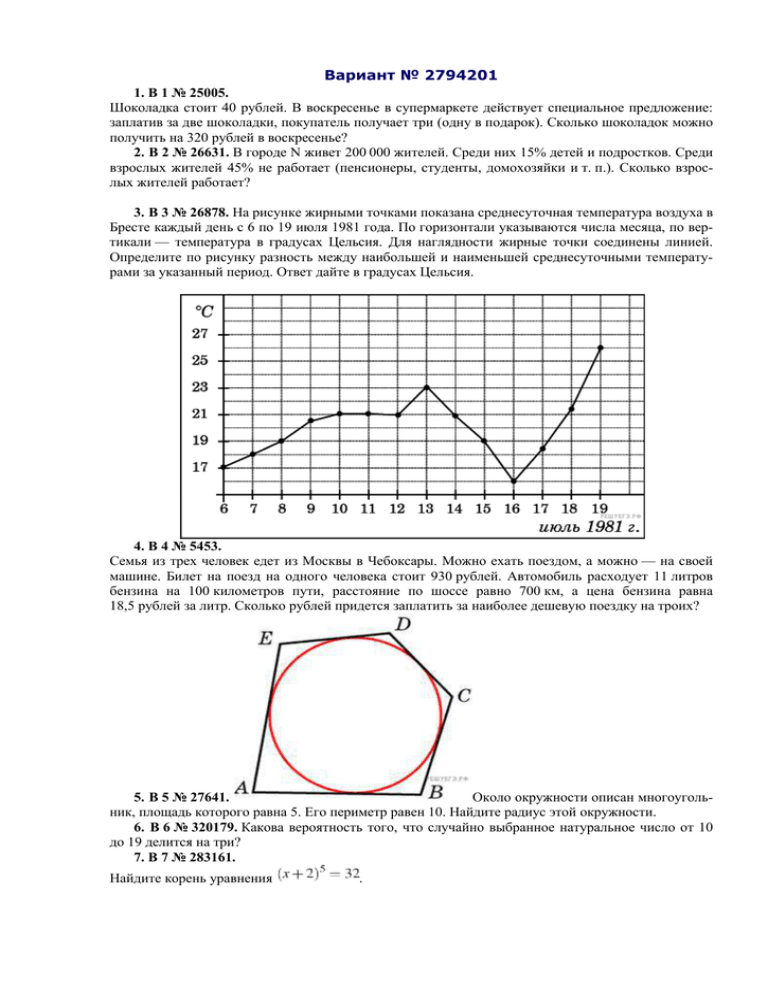
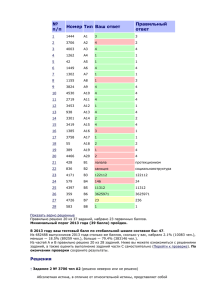
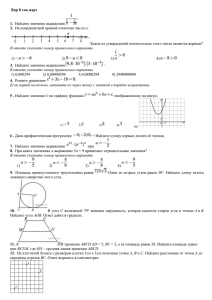
Вариант № 2794201
1. B 1 № 25005.
Шоколадка стоит 40 рублей. В воскресенье в супермаркете действует специальное предложение:
заплатив за две шоколадки, покупатель получает три (одну в подарок). Сколько шоколадок можно
получить на 320 рублей в воскресенье?
2. B 2 № 26631. В городе N живет 200 000 жителей. Среди них 15% детей и подростков. Среди
взрослых жителей 45% не работает (пенсионеры, студенты, домохозяйки и т. п.). Сколько взрослых жителей работает?
3. B 3 № 26878. На рисунке жирными точками показана среднесуточная температура воздуха в
Бресте каждый день с 6 по 19 июля 1981 года. По горизонтали указываются числа месяца, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки соединены линией.
Определите по рисунку разность между наибольшей и наименьшей среднесуточными температурами за указанный период. Ответ дайте в градусах Цельсия.
4. B 4 № 5453.
Семья из трех человек едет из Москвы в Чебоксары. Можно ехать поездом, а можно — на своей
машине. Билет на поезд на одного человека стоит 930 рублей. Автомобиль расходует 11 литров
бензина на 100 километров пути, расстояние по шоссе равно 700 км, а цена бензина равна
18,5 рублей за литр. Сколько рублей придется заплатить за наиболее дешевую поездку на троих?
5. B 5 № 27641.
Около окружности описан многоугольник, площадь которого равна 5. Его периметр равен 10. Найдите радиус этой окружности.
6. B 6 № 320179. Какова вероятность того, что случайно выбранное натуральное число от 10
до 19 делится на три?
7. B 7 № 283161.
Найдите корень уравнения
.
8. B 8 № 27409.
,
В треугольнике
. Найдите
угол
равен 90°, тангенс внешнего угла при вершине
равен
.
9. B 9 № 119975. Материальная точка движется прямолинейно по закону
(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 9 с.
10.
де
B 10 № 917.
В
известно, что
11. B 11 № 99467.
прямоугольном
параллелепипе-
Найдите длину ребра
.
Найдите
, если
.
12. B 12 № 27996. Водолазный колокол, содержащий в начальный момент времени
моля
воздуха объeмом
л, медленно опускают на дно водоeма. При этом происходит изотермическое сжатие воздуха до конечного объeма . Работа, совершаемая водой при сжатии воздуха,
определяется выражением
ратура воздуха. Какой объeм
вершена работа в 10350 Дж?
(Дж), где
– постоянная, а
– темпе(в литрах) станет занимать воздух, если при сжатии газа была со-
13. B 13 № 27048.
В сосуд, имеющий форму правильной
треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет нахо-
диться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4
раза больше, чем у первого? Ответ выразите в см.
14. B 14 № 99596. Два мотоциклиста стартуют одновременно в одном направлении из двух
диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
15. B 15 № 26713. Найдите точку максимума функции
16. C 1 № 485987.
.
а) Решите уравнение
б) Укажите корни уравнения, принадлежащие отрезку
17. C 2 № 484567. В правильной шестиугольной пирамиде SABCDEF стороны основания которой равны 1, а боковые ребра равны 2, найдите угол между прямыми SB и CD.
18. C 3 № 500817. Решите систему неравенств
19. C 4 № 485990. Дан треугольник
со сторонами
и
На стороне
взята точка
а на отрезке
— точка
причем
и
Окружность с
центром проходит через точку
Найдите расстояние от точки до точки пересечения этой
окружности с прямой
20. C 5 № 500004. Найдите все значения параметра a, при каждом из которых систе-
ма
имеет ровно два решения.
21. C 6 № 501694. Задумано несколько (не обязательно различных) натуральных чисел. Эти
числа и их все возможные суммы (по 2, по 3 и т. д.) выписывают на доску в порядке неубывания.
Если какое-то число n, выписанное на доску, повторяется несколько раз, то на доске оставляется
одно такое число n, а остальные числа, равные n, стираются. Например, если задуманы числа 1, 3,
3, 4, то на доске будет записан набор 1, 3, 4, 5, 6, 7, 8, 10, 11.
а) Приведите пример задуманных чисел, для которых на доске будет записан набор 2, 4, 6, 8,
10.
б) Существует ли пример таких задуманных чисел, для которых на доске будет записан набор
1, 3, 4, 5, 6, 8, 10, 11, 12, 13, 15, 17, 18, 19, 20, 22?
в) Приведите все примеры задуманных чисел, для которых на доске будет записан набор 7, 8,
10, 15, 16, 17, 18, 23, 24, 25, 26, 31, 33, 34, 41.
Решения
↑ Задание 1 № 25005 тип B1 (решено неверно или не решено)
Шоколадка стоит 40 рублей. В воскресенье в супермаркете действует специальное предложение:
заплатив за две шоколадки, покупатель получает три (одну в подарок). Сколько шоколадок можно
получить на 320 рублей в воскресенье?
Решение.
На 320 рублей можно купить 8 шоколадок по 40 рублей. Еще 4 будут даны в подарок. Всего
можно будет получить 12 шоколадок.
О т в е т : 12.
Ваш ответ: нет ответа. Правильный ответ: 12
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 2 № 26631 тип B2 (решено неверно или не решено)
В городе N живет 200 000 жителей. Среди них 15% детей и подростков. Среди взрослых жителей 45% не работает (пенсионеры, студенты, домохозяйки и т. п.). Сколько взрослых жителей работает?
Решение.
Численность детей в городе N составляет 200 000 0,15 = 30 000. Численность взрослого населения 200 000 − 30 000 = 170 000 человек. Из них не работает 170 000 0,45 = 76 500 человек. Значит, работает 170 000 − 76 500 = 93 500 человек.
О т в е т : 93 500.
Ваш ответ: нет ответа. Правильный ответ: 93500
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 3 № 26878 тип B3 (решено неверно или не решено)
На рисунке жирными точками показана среднесуточная температура воздуха в Бресте каждый
день с 6 по 19 июля 1981 года. По горизонтали указываются числа месяца, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку разность между наибольшей и наименьшей среднесуточными температурами за указанный
период. Ответ дайте в градусах Цельсия.
Решение.
Из графика видно, что наибольшая и наименьшая температура за указанный период составляла 26 °C и 16 °C соответственно (см. рисунок). Их разность равняется 10 °C.
О т в е т : 10.
Ваш ответ: нет ответа. Правильный ответ: 10
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 4 № 5453 тип B4 (решено неверно или не решено)
Семья из трех человек едет из Москвы в Чебоксары. Можно ехать поездом, а можно — на своей
машине. Билет на поезд на одного человека стоит 930 рублей. Автомобиль расходует 11 литров
бензина на 100 километров пути, расстояние по шоссе равно 700 км, а цена бензина равна
18,5 рублей за литр. Сколько рублей придется заплатить за наиболее дешевую поездку на троих?
Решение.
Стоимость поездки на поезде для троих человек будет составлять 930 3 = 2790 руб. Расход
бензина на 700 км пути составит 7 раз по 11 литров т. е. 77 литров. Его стоимость
77 18,5 = 1424,5 руб.
Стоимость самой дешевой поездки составляет 1424,5 рубля.
О т в е т : 1424,5.
Ваш ответ: нет ответа. Правильный ответ: 1424,5
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 5 № 27641 тип B5 (решено неверно или не решено)
торого
равна
5.
Его
периметр
Около окружности описан многоугольник, площадь коравен 10. Найдите радиус этой окружности.
Решение.
Радиус вписанной в многоугольник окружности равен отношению его площади к полупериметру. Пусть площадь равна S, периметр равен P, радиус окружности равен R. Тогда
.
О т в е т : 1.
Ваш ответ: нет ответа. Правильный ответ: 1
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 6 № 320179 тип B6 (решено неверно или не решено)
Какова вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на
три?
Решение.
Натуральных чисел от 10 до 19 десять, из них на три делятся три числа: 12, 15, 18. Следовательно, искомая вероятность равна 3:10 = 0,3.
О т в е т : 0,3.
Ваш ответ: нет ответа. Правильный ответ: 0,3
Гость 22.04.2013 18:35:
Требуется ли включать 19, если сказано до 19?
Константин Лавров (Санкт-Петербург):
Да. Требуется. Хотя бы потому, что в противном случае ответ нельзя будет записать в бланк ЕГЭ.
Обсудить ВКонтакте Сообщить об ошибке
↑ Задание 7 № 283161 тип B7 (решено неверно или не решено)
Найдите корень уравнения
.
Решение.
Извлекая корень пятой степени из обеих частей уравнения, получаем
, откуда
.
Ваш ответ: нет ответа. Правильный ответ: 0
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 8 № 27409 тип B8 (решено неверно или не решено)
В треугольнике
,
угол
равен 90°, тангенс внешнего угла при вершине
.
Найдите
Решение.
.
Ответ: 4.
Ваш ответ: нет ответа. Правильный ответ: 4
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 9 № 119975 тип B9 (решено неверно или не решено)
равен
.
Материальная точка движется прямолинейно по закону
(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее
скорость
(в
м/с)
в
момент
времени t = 9 с.
Решение.
Найдем закон изменения скорости:
.
При t = 9 c имеем:
м/с.
О т в е т : 60.
Ваш ответ: нет ответа. Правильный ответ: 60
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 10 № 917 тип B10 (решено неверно или не решено)
В прямоугольном параллелепипеде
вестно,
что
Найдите
Решение.
по теореме Пифагора
Тогда длина ребра
О т в е т : 2.
равна
длину
изребра
.
Ваш ответ: нет ответа. Правильный ответ: 2
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 11 № 99467 тип B11 (решено неверно или не решено)
Найдите
, если
.
Решение.
Выполним преобразования:
.
О т в е т : 71.
Ваш ответ: нет ответа. Правильный ответ: 71
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 12 № 27996 тип B12 (решено неверно или не решено)
Водолазный колокол, содержащий в начальный момент времени
моля воздуха
объeмом
л, медленно опускают на дно водоeма. При этом происходит изотермическое сжатие воздуха до конечного объeма . Работа, совершаемая водой при сжатии воздуха, определяется выражением
духа. Какой объeм
бота
(Дж), где
– постоянная, а
– температура воз(в литрах) станет занимать воздух, если при сжатии газа была совершена рав
10350
Дж?
Решение.
Задача сводится к решению уравнения
янной
, температуры воздуха
духа
л:
при заданных значениях постоК, количества воздуха
моль и объема воз-
л.
О т в е т : 2.
Ваш ответ: нет ответа. Правильный ответ: 2
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 13 № 27048 тип B13 (решено неверно или не решено)
В сосуд, имеющий форму правильной треугольной призмы,
налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды,
если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у
первого?
Ответ
выразите
в
см.
Решение.
Объем сосуда выражается через его высоту и сторону основания как
чении стороны основания
5 см.
в 4 раза уровень воды
. При увели-
уменьшится в 16 раз и будет равен
О т в е т : 5.
Ваш ответ: нет ответа. Правильный ответ: 5
Гость 02.06.2013 21:37:
Правильный
1/2ah*80=4*1/2ah*x
80=4x
x=20
Sтреугольника=1/2ah
Александр Иванов (Санкт-Петербург):
так
высота
треугольника
тоже
1/2ah*80=1/2*4a*4h*x
80=16x
x=5
Обсудить ВКонтакте Сообщить об ошибке
ответ:20
увеличится
в
4
раза:
↑ Задание 14 № 99596 тип B14 (решено неверно или не решено)
Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
Решение.
Пусть
км/ч — скорость первого мотоциклиста, тогда скорость второго мотоциклиста
равна
км/ч. Пусть первый раз мотоциклисты поравняются через часов. Для того, чтобы
мотоциклисты поравнялись, более быстрый должен преодолеть изначально разделяющее их расстояние, равное половине длины трассы. Поэтому
.
Таким образом, мотоциклисты поравняются через
часа или через 20 минут.
О т в е т : 20.
Приведём другое решение.
Быстрый мотоциклист движется относительно медленного со скоростью 21 км в час, и должен
преодолеть разделяющие их 7 км. Следовательно, на это ему потребуется одна треть часа.
Ваш ответ: нет ответа. Правильный ответ: 20
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 15 № 26713 тип B15 (решено неверно или не решено)
Найдите
точку
максимума
функции
.
Решение.
Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
Искомая точка максимума
О т в е т : −15.
.
Ваш ответ: нет ответа. Правильный ответ: -15
Гость 01.05.2012 08:49:
Объясните пожалуйста, откуда берется (-1)? Просто не вижу отличий между предыдущими
заданиями, а принцип решения разный. Спасибо.
Служба поддержки:
Мы вычисляем производную сложной функции, умножаем на коэффициент перед x.
Обсудить ВКонтакте Сообщить об ошибке
Проверка части С
Пожалуйста, оцените решения заданий части С самостоятельно, руководствуясь указанными
критериями.
Задание С1 № 485987
Критерии оценивания выполнения задания
Верно решено уравнение и произведен отбор корней
Баллы
2
Верно решено уравнение, но не произведен или не обоснован отбор корней, принадлежащих данному отрезку, или верно указаны все корни, принадлежащие данному
1
отрезку, но решение простейших тригонометрических уравнений не доведено до конца
Решение не соответствует ни одному из критериев, перечисленных выше
0
Максимальный балл
2
а) Решите уравнение
б) Укажите корни уравнения, принадлежащие отрезку
Решение.
а) Преобразуем уравнение:
Значит,
или
В первом случае
во втором случае
Первая серия решений входит во вторую.
б) Отметим решения на тригонометрической окружности.
Отрезку
принадлежат корни
и
О т в е т : а)
б)
Ваша оценка (баллов):
Виталий Сагалаев (Волжский) 16.08.2013 10:46:
В
первом
случае
Там
получается
,
Разве нет?
Константин Лавров (Санкт-Петербург):
А есть разница, если
Обсудить ВКонтакте Сообщить об ошибке
и
а
т.
не
д.
плюс.
Задание С2 № 484567
Критерии оценивания выполнения задания
Баллы
Обоснованно получен верный ответ
2
Решение содержит обоснованный переход к планиметрической задаче, но получен
неверный ответ или решение не закончено
1
Решение не соответствует ни одному из критериев, перечисленных выше
0
Максимальный балл
2
В правильной шестиугольной пирамиде SABCDEF стороны основания которой равны 1, а боковые ребра равны 2, найдите угол между прямыми SB и CD.
Решение.
Вместо прямой CD рассмотрим параллельную ей прямую BE. Искомый угол равен углу SBE.
Треугольник SBE равносторонний, поскольку большая диагональ правильного шестиугольника
вдвое больше его стороны:
Ответ:
.
. Следовательно,
.
Ваша оценка (баллов):
Обсудить ВКонтакте
Сообщить об ошибке
Задание С3 № 500817
Критерии оценивания выполнения задания
Обосновано получен верный ответ
Баллы
3
Для обоих неравенств системы обоснованно получены верные ответы, но не проведено
2
обоснованного сравнения значений конечных точек найденных промежутков
Для одного из двух неравенств системы обоснованно получен верный ответ
1
Решение не соответствует ни одному из критериев, перечисленных
0
Максимальный балл
3
Решите систему неравенств
Решение.
1.
но
ем
Неравенство
запишем
в
виде
Относитель-
неравенство
имеет
вид:
откуда
получаТогда
2. Второе неравенство системы определено на области, задаваемой системой неравенств
то есть при
и
При допустимых значениях переменной получаем:
С учетом области допустимых значений переменной получаем решение второго неравенства
системы:
Сравним
и
Так как
то
следовательно,
Решение системы неравенств:
Ответ:
Ваша оценка (баллов):
Обсудить ВКонтакте
Сообщить об ошибке
Задание С4 № 485990
Критерии оценивания выполнения задания
Обоснованно получен верный ответ
Баллы
3
Рассмотрена верная геометрическая конфигурация. Найдено одно верное значение ис2
комой величины
Рассмотрена верная геометрическая конфигурация. Найдено одно значение искомой
величины, неправильное из-за арифметической ошибки
1
Решение не соответствует ни одному из критериев, перечисленных выше
0
Максимальный балл
3
Дан треугольник
точка
а на отрезке
со сторонами
— точка
причем
и
и
На стороне
взята
Окружность с цен-
тром
проходит через точку
окружности с прямой
Найдите расстояние от точки
до точки пересечения этой
Решение.
Проведем через вершину прямую, параллельную
Пусть — точка ее пересечения с
прямой
а
— точка пересечения
и
Треугольник
подобен треугольнику
с коэффициентом
поэтому
Значит, треугольник
равен
треугольнику
по стороне и двум прилежащим к ней углам. Тогда
— середина стороны
Следовательно,
— медиана треугольника
Медиана прямоугольного треугольника, проведенная из прямого угла равна половине гипотенузы, значит
Через вершину
прямой
проведем прямую, параллельную
Треугольник
му
щим к ней углам. Поэтому
Окружность с центром
но,
точка
подобен треугольнику
Тогда треугольники
— середина
проходит через точку
Пусть
— точка ее пересечения с
с коэффициентом
и
равны по стороне и двум прилежа-
и при этом
— радиус этой окружности. Треугольник
прямоугольный,
— одна из точек пересечения прямой
и окружности.
Пусть — вторая точка пересечения окружности с прямой
ный и опирающийся на диаметр
так что
то есть
Отсюда
О т в е т : 7,5 или 7,2.
поэто-
Следовательа
Тогда угол
— вписан— высота треугольника
Ваша оценка (баллов):
Обсудить ВКонтакте
Сообщить об ошибке
Задание С5 № 500004
Критерии оценивания выполнения задания
Баллы
Обоснованно получен верный ответ
4
С помощью верного рассуждения получены искомые значения, возможно неверные,
из-за одной допущенной вычислительной ошибки (описки)
3
С помощью верного рассуждения получено одно значение параметра (возможно неверное из-за одной вычислительной ошибки), а второе значение потеряно в результате
2
ошибки (например «потеряны» модули)
Задача сведена к исследованию взаимного расположения графиков неравенства и
уравнения (приведен правильный рисунок)
1
Решение не соответствует ни одному из критериев, перечисленных выше
0
Максимальный балл
4
Найдите
ма
все
значения
параметра a,
при
каждом
из
которых
систе-
имеет ровно два решения.
Решение.
Неравенство (1) задает пару вертикальных углов
на координатной плоскости Oxy (см. рисунок). Графиком уравнения (2) является окружность радиуса
, центр которой ― точка
― лежит на прямой
. Поскольку оба
графика симметричны относительно прямой
, система будет иметь ровно два решения
тогда и только тогда, когда расстояние PK от центра окружности до прямой
будет равняться радиусу
дим:
зом,
, где
данной окружности. Из треугольника POK нахо― угловой коэффициент прямой
. Таким обра-
,
,
, откуда
.
Окончательно получаем:
Ответ:
или
,
,
или
.
.
Ваша оценка (баллов):
Обсудить ВКонтакте
Сообщить об ошибке
Задание С6 № 501694
Критерии оценивания выполнения задания
Баллы
Верно получены все перечисленные (см. критерий на 1 балл) результаты
4
Верно получены три из перечисленных (см. критерий на 1 балл) результатов
3
Верно получены два из перечисленных (см. критерий на 1 балл) результатов
2
Верно получен один из следующих результатов: — обоснованное решение п. а; —
обоснованное решение п. б; — обоснованная оценка количества задуманных чисел в
п. е; — оба набора задуманных чисел в п. в
1
Решение не соответствует ни одному из критериев, перечисленных выше
0
Максимальный балл
4
Задумано несколько (не обязательно различных) натуральных чисел. Эти числа и их все возможные суммы (по 2, по 3 и т. д.) выписывают на доску в порядке неубывания. Если какое-то
число n, выписанное на доску, повторяется несколько раз, то на доске оставляется одно такое
число n, а остальные числа, равные n, стираются. Например, если задуманы числа 1, 3, 3, 4, то на
доске будет записан набор 1, 3, 4, 5, 6, 7, 8, 10, 11.
а) Приведите пример задуманных чисел, для которых на доске будет записан набор 2, 4, 6, 8,
10.
б) Существует ли пример таких задуманных чисел, для которых на доске будет записан набор
1, 3, 4, 5, 6, 8, 10, 11, 12, 13, 15, 17, 18, 19, 20, 22?
в) Приведите все примеры задуманных чисел, для которых на доске будет записан набор 7, 8,
10, 15, 16, 17, 18, 23, 24, 25, 26, 31, 33, 34, 41.
Решение.
а) Задуманные числа 1, 1, 1, 1, 1, 1, 1 дают требуемый набор, записанный на доске.
б) Поскольку задуманные числа натуральные, то наименьшее число в наборе — это наименьшее из задуманных чисел, а наибольшее число в наборе — это сумма всех задуманных чисел.
Среди чисел записанного набора должна быть сумма всех чисел, кроме наименьшего, то есть
22 − 1 = 21. Но этого числа нет в наборе, поэтому не существует примера таких задуманных чисел,
для которого на доске будет выписан набор из условия.
в) Число 7 — наименьшее число в наборе — является наименьшим из задуманных чисел, а
наибольшее число в наборе — это сумма всех задуманных чисел. Поэтому количество задуманных
чисел не превосходит целой части —, то есть 5. Кроме того, числа 9 и 11 меньше, чем сумма двух
чисел 7, поэтому они также являются задуманными. Значит, сумма оставшихся задуманных чисел
равна 41 − 7 − 9 − 11 = 14. Таким образом, так как наименьшее задуманное число равно 7, оставшиеся задуманные числа — это 7 и 7 или 14. Для задуманных чисел 7, 7, 7, 9, 11 и 7, 9, 11, 14 на
доске будет записан набор, данный в условии.
О т в е т : а) 1, 1, 1, 1, 1, 1, 1; б) нет; в) 7, 7, 7, 9, 11 или 7, 9, 11, 14.
Ваша оценка (баллов):