Курсовая работа

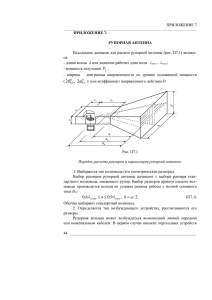
Министерство образования и науки Российской Федерации
ФГАОУ ВО «Северо-Восточный федеральный университет им. М.К.
Аммосова»
Физико-технический институт
Кафедра «Радиофизика»
Курсовая работа по дисциплине “Антенно-фидерные устройства”
Выполнил: студент 1
курса магистратуры
группы М-РТ-19 ФТИ
СВФУ
Ефремов Д.Д
Проверил;:
Федоров В.Н
Якутск 2019 г.
Содержание
Задание
Обоснование выбора методики расчета
Расчетная часть
1. Расчет параметров антенны
2. Выбор параметров облучателя
3. Расчет ДН облучателя
4. Расчет амплитудного распределения по раскрыву
5. Расчет ДН зеркальной антенны
Заключение
Список использованной литтературы
Задание
Спроектировать
параболическую
антенну
для
приема
линейно-поляризованного сигнала.
Исходные данные:
f 0  4 ГГц - рабочая частота;
K y  35 дБ - коэффициент усиления антенны;
1  19 дБ - допустимый уровень первых боковых лепестков.
1. Обоснование выбора методики расчета
Теоретические сведения
Параболические
антенны
являются
одним
из
наиболее
распространенных типов антенн, используемых в современных
радиотехнических системах различного назначения (радиорелейные
системы связи, радиолокация, спутниковые системы связи и вещания и
т.д.). Они применяются в различных диапазонах волн, от метровых до
миллиметровых. Наибольшее распространение получили антенны с
зеркалами в виде параболоида вращения, усеченного параболоида и
параболического цилиндра. Такие антенны обладают высоким КПД,
возможностью формирования разнообразных ДН при относительной
простоте конструкции, малой шумовой температурой.
Параболическая
антенна
состоит
из
двух
элементов:
металлического параболического профиля и облучателя, помещенного
в фокусе зеркала. Схема антенны с параболическим зеркалом
представлена на рис.1.
Рисунок 1. Схема параболической антенны
Принцип работы антенны основан на том, что сумма расстояний
от фокуса F до зеркала и от зеркала до апертуры является величиной
постоянной. Следовательно, если в фокусе расположен источник
сферической
преобразуется
волны,
в
то
после
плоскую,
и
отражения
от
излучающий
зеркала
раскрыв
волна
антенны
возбуждается синфазно. При равномерном облучении зеркала ДН
параболической антенны является иглообразной. При облучении
только части зеркала можно получить плоскую ДН.
Параболический профиль зеркала описывается в прямоугольной
системе координат уравнением:
у 2  4 fx , (1)
где f - фокусное расстояние.
Параболическая антенна характеризуется геометрическими
размерами R - радиусом раскрыва (апертуры), f - фокусным
расстоянием и  0 - углом раскрыва, которые связаны соотношением:
R  2  f  tg  0 2 . (2)
параболический антенна амплитудный сигнал
С точки зрения формирования поля излучения и диаграммы
направленности антенну с зеркалом в виде параболоида вращения
можно рассматривать как синфазно возбужденный круглый раскрыв,
амплитудное
распределение
возбуждающего
поля
на
котором
описывается некоторой функцией. Вид этой функции определяет
форму и параметры ДН антенны при заданном размере раскрыва.
Облучатели зеркальных антенн
Облучатель является важнейшим элементом параболической
антенны, определяющий её характеристики. В качестве облучателей
используются
слабонаправленные
антенны,
удовлетворяющие
следующим основным требованиям:
ДН
должна
обеспечивать
необходимое
амплитудное
распределение поля на излучающем раскрыве зеркала;
облучатель должен иметь фазовый центр, совмещенный с
фокусом зеркала;
рабочая полоса частот должна соответствовать заданной;
поперечные размеры облучателя должны быть минимальны для
уменьшения затенения зеркала.
Наиболее применимы на практике облучатели следующих типов:
вибраторные, волноводно-рупорные, щелевые.
Волноводно-рупорные облучатели находят широкое применение
в связи с простотой конструкции, возможностью формирования ДН
требуемой ширины в обеих плоскостях и хорошими диапазонными
свойствами.
Простейшим облучателем данного типа является открытый конец
волновода. Однако такая антенна обладает тем недостатком, что из-за
резкого изменения условий распространения при переходе волновода к
свободному пространству значительная часть электромагнитной волны
отражается от открытого
конца. Волновод оказывается плохо
согласованным с окружающим пространством. Избежать этого можно
плавным увеличением размеров поперечного сечения волновода, т.е.
придания ему формы рупора.
Существуют различные типы рупоров. Рупор, образованный
плавным увеличением поперечного сечения круглого волновода,
называется коническим. При плавном переходе от волновода к рупору
структура поля в нем напоминает структуру поля в волноводе.
Облучатель в виде конического рупора был выбран в данной курсовой
работе.
Диаграмма направленности круглого волновода по форме близка
к
параболоиду вращения, что позволяет получить достаточно
равномерное, относительно оси, облучение зеркала, необходимое для
создания «игольчатой» диаграммы направленности. Кроме того, при
этом значительно уменьшается перекрестная поляризация, поскольку
волна Н11, распространяющаяся в круглом волноводе, сама имеет
перекрестную составляющую, но направленную противоположно
перекрестной составляющей волны, отраженной от зеркала при
облучении его линейно-поляризованным полем.
При расчете конического рупорного облучателя необходимо
учитывать, что рупорная антенна имеет примерно квадратичное
фазовое распределение. Максимальный сдвиг фаз на краю раскрыва:
 max
  a 2ð

  L , (3)
где
ap
- радиус раскрыва рупора, L - длина рупора. Допустимый

фазовый сдвиг конического рупора доп  100 . Параметры рупора
необходимо выбирать удовлетворяющими условию.
Диаметр рупорной антенны рассчитывается по формуле:
d p  06    sin   0   cos   0  1  cos   0  
. (4)
Оптимальная длинна рупора определяется из уравнения:
Lопт 
0.3  cos( 0 )
1  cos( 0 ) . (5)
ДН конической рупорной антенны можно рассчитать по формуле
[2]:
В плоскости Е:
 d

2  J 1   p  sin   

 


Fe ( )  cos 2   
d
2
  p  sin  

, (6)
В плоскости Н:
 d

2  J 1'    p  sin   

 


Fh ( )  cos 2   
2
2
dp


J1( x)
'
1   0.543   sin   
J1 ( x)  J 0( x) 


 , (7)
x
где J1(x) - функция Бесселя первого рода, производная функции
Бесселя по аргументу.
Расчет ДН зеркальных антенн
Существуют два приближенных метода определения
направленных свойств параболической антенны: токовый и
апертурный. Токовый метод предлагает расчет ДН параболической
антенны по распределению токов на поверхности зеркала. Зная
распределение токов на поверхности зеркала можно определить
направленные свойства параболической антенны. Для этого
необходимо проинтегрировать по всей поверхности зеркала выражение
для напряженности поля, создаваемого элементом поверхности
зеркала, рассматривая его как элементарный электрический вибратор.
Токовый метод обеспечивает достаточно точные результаты в пределах
главного бокового лепестка антенны и прилегающих к нему боковых
лепестков. Однако недостатком метода является его сложность и
громоздкость. В данной работе расчет ведется по апертурному методу.
Рассмотрим в качестве излучающей плоскую поверхность
раскрыва. Можно определить напряженность поля в любой точке
пространства по распределению поля на поверхности раскрыва. Для
приближенного определения распределения поля на поверхности
раскрыва можно воспользоваться методом геометрической оптики,
согласно которому каждому лучу облучателя, падающему на
поверхность зеркала, соответствует луч, отраженный от этой
поверхности. Если облучатель расположен в фокусе параболоида, все
отраженные от поверхности антенны лучи оказываются
параллельными (плоская волна), и поэтому плотность энергии на пути
от поверхности параболоида до излучающей поверхности не меняется.
На пути от облучателя до поверхности параболоида амплитуда лучей
убывает обратно пропорционально расстоянию. Таким образом, если в
фокусе параболоида размещен облучатель с диаграммой
направленности Fобл  ,  , то распределение поля Е  ,  в раскрыве
антенны по методу геометрической оптики определится равенством
[1]:
 
Е ( , )  Fобл  ,   cos2  
 2  . (8)
Распределение напряжённости по апертуре антенны можно
аппроксимировать при помощи полинома:
2


Q( R ' )   a n  1  R '
n 0
R' 

n
, (9)

R ,  - координата апертуры антенна, R- радиус
где
раскрыва антенны.
ДН параболической антенны найдем по формуле:
F   
6a0 1 ( )  3a1 2 ( )  2a2  3 ( )
6a0  3a1  2a2
(10)
2. Расчетная часть
1. Расчет параметров антенны
Выберем КПД антенны   0.85 , коэффициент использования
поверхности антенны КИП=0.7.
Коэффициент направленного действия антенны:
D
Ky
 ; (11)
1585
D
 1865  32.7 дБ
0.85
.
С другой стороны:
D
4  S

2
 КИП
. (12)
Отсюда площадь раскрыва зеркала:
D  2
S
4  КИП ; (13)
1865  0.06 2
S
 0.76 м 2
4  0.7
.
Радиус раскрыва параболоида:
R
S
 ; (14)
R
0.76
 0.49
3.14
м.
Зная диаметр раскрыва зеркала D =0.98 м, выберем фокусное
расстояние, учитывая что f   0.35  0.5  D :
f  0.35  0.98  0.34 м .
Угол раскрыва параболоида:
R
2 f , (15)
0.49
 0  2  arctg
 71.5
2  0.34
.
 0  2  arctg
В итоге параметры антенны:
R  0.49 м
f  0.34 м
 0  71.5
  0.06 м
Профиль зеркала:
Рисунок 2. Профиль зеркала
2.2 Выбор параметров облучателя
В
качестве
облучателя
выбран
конический
рупор.
Для
обеспечения одномодового режима в круглом волноводе необходимо
выполнения условия:
2.61a    3.41a ,
где а - радиус волновода. Поскольку   0.06 м , диаметр
волновода находится в пределах:
0.034 м  2a  0.046 м .
Выберем волновод типа 1Б31ЕС-С56 с параметрами:
Таблица 11Б31ЕС-С56
Внутренний
диаметр,
мм
d
38.1
Толщина стенок,
мм
Затухание для медных
стенок
1.650
f, ГГц
5.534
, дБ/м
0.0473
Критическая частота,
ГГц
4.61
Определим параметры рупора.
Зная угол облучения рупором краёв малого зеркала, вычислим
радиус раскрыва облучателя, воспользовавшись формулой для ширины
диаграммы направленности конического рупора.

Зададимся шириной ДН рупора 0.5  143 .
60  
 0.5 ; (16)
60  0.06
ap 
 0.025
143
.
ap 
Зная диаметр рупора, вычислим его угол раскрыва по формуле:
d p  06    sin   0   cos   0  1  cos   0  
,
 0  50 .

Оптимальная длина рупора:
Lопт 
Lîïò
0.3   cos  0
1  cos  0
,
0.3  0.06  cos 50

 0.032
1  cos 50
м.
Исходя из геометрических размеров, выберем длину рупора:
L  0.05 м.
Максимальная фазовая ошибка на краю раскрыва:
 max
 max
  a 2p

L ,
3.14  0.0252

 0.65  37   100
0.06  0.05
Фазовая ошибка является допустимой.
2.3 Расчет ДН облучателя
В плоскости Е:
d


2  J 1   p  sin   

 


Fe ( )  cos 2   
d
2
  p  sin  

,
В плоскости Н:
 d

2  J 1'    p  sin   

 


Fh ( )  cos 2   
2
2
dp


1   0.543   sin   


 .
ДН в декартовой системе координат:
Рисунок 3. ДН рупора в декартовой системе координат
ДН в полярной системе координат:
Рисунок 4. ДН рупора в полярной системе координат
2.4 Расчет амплитудного распределения по раскрыву
Напряженность поля в раскрыве зеркала для Е и Н плоскостей:
 
Åe ( )  Fe    cos 2  
 2 ,
 
Åh ( )  Fh    cos 2  
 2 .
Нормированная координата в точке раскрыва [1]:
 
tg  

2
R'    
R
 
tg  0 
 2  (17)
Выразим угол  через координату раскрыва зеркала  :


   tg  0
 2
  2  arctg 
R







 . (18)
Тогда напряженность поля в раскрыве зеркала для Е и Н
плоскостей:




   
   


   tg  0   
   tg  0   

 2     cos2  arctg 
 2  
Åe (  )  Fe  2  arctg 





R
R



 

 












   tg  0


 2
Å h (  )  Fh  2  arctg 
R







  
   

   tg  0   

    cos 2  arctg 
 2  




R

 

 






(19)
График амплитудного распределения в раскрыве зеркала:
Рисунок 5. Амплитудное распределение напряженности в
раскрыве зеркала
2.5 Расчет ДН зеркальной антенны
Аппроксимируем фактическое распределение поля в раскрыве
параболоида интерполяционным полиномом [3]:
2


Q( R' )   a n  1  R '
n 0

n
Из графика амплитудного распределения в раскрыве находим
коэффициенты интерполяционного полинома по формулам:
a0  a1  a2  1
a0  a1 (1  0,5 2 )  a2 (1  0,5 2 ) 2  F (0.5)
,
где a 0 - значение относительной напряженности поля на краю
раскрыва, F (0.5) - значение относительной напряженности поля на
середине раскрыва. Для Е-плоскости:
ae0  0.73
F (0.5)  0.92
Из уравнений получаем коэффициенты полинома аппроксимации
для Е плоскости:
a e 0  0.73
a e1  0.2033
a e 2  0.0667
Для H-плоскости:
a h 0  0.79
F (0.5)  0.95
Из уравнений получаем коэффициенты полинома аппроксимации
для Е плоскости:
a h 0  0.79
a h1  0.223
a h 2  0.013
График полинома аппроксимации представлен на рис.6:
Рисунок 6. График амплитудного распределения по раскрыву и
аппроксимирующей функции.
Для определения диаграммы направленности антенны, найдем
2   первого, второго и третьего порядка.
лямбда-функции
u   
 sin  
1   

2  1
u  
1
 Jn 1 u   
2
2   
2  2
3   
2  3
где
u  
2
3
u  
u ( ) 
3
 Jn 2 u   
 Jn 3 u   
,
2    R  sin 

.
Диаграмма направленности зеркальной антенны для Е плоскости:
F2 e   
6a e 0  1 ( )  3a e1  2 ( )  2a e 2  3 ( )
6a e 0  3a e1  2a e 2
Диаграмма направленности зеркальной антенны для Н
плоскости:
F2 h   
6a h 0  1 ( )  3a h1  2 ( )  2a h 2  3 ( )
6a h 0  3a h1  2a h 2
Рисунок 7. ДН зеркальной антенны
По графику распределения определим ширину главного лепестка:
  2  1.14  2.29 
Нормированная логарифмическая ДН зеркальной антенны:
Рисунок 8. Нормированная ДН зеркальной антенны
Уровень первых боковых лепестков из графика:
  25 дБ.
Такой уровень соответствует значению коэффициента
использования поверхности  a  0.79 [1, табл.5.1].
Коэффициент направленного действия антенны:
D
4  S

2
 КИП 
4    0.76
 0.79  2094  33.2 дБ
0.062
. (20)
Заключение
В данном курсовом проекте был проведен расчет зеркальной
параболической антенны для приема линейно поляризованного
сигнала. В качестве облучателя антенны был выбран конический
рупор. Были определены КНД антенны, ширина ДН антенны, уровень
боковых лепестков и построена ДН антенны.
Антенна
имеет
относительно
удовлетворяет поставленной задаче.
хорошую
направленность,
СПИСОК ЛИТЕРАТУРЫ
1 В.Л.
Гончаров,
А.Л.
Патлах,
А.Р.
Склюев,
А.Х.
Хорош.
Малошумящие однозеркальные параболические антенны, Алматы
1998;
2 Д.И. Вознесенский. Антенны и устройства СВЧ. Проектирование
фазированных антенных решеток. М: Советское радио, 1994;
3 Д.М. Сазонов. Антенны и устройства СВЧ. - М.: Высшая школа,
1988
4 Г.М. Кочержевский, Г.А. Ерохин, Н.Д. Козырев. Антенно-фидерные
устройства.- М.: Радио и связь, 1989;
5 В.Ф. Хмель, А.Ф. Чаплин, И.И. Шумлянский. Антенны и устройства
СВЧ. - Киев.: Вища школа, 1990;
6 Марков Г.Т. Сазанов Д.М. «Антенны», М: Энергия, 1975;
7 Айзенберг Г.З. «Антенны ультракоротких волн», М: Связьиздат,
1957;