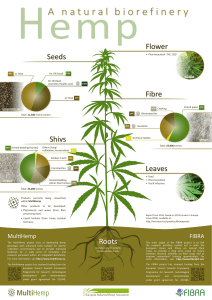
Fibre Volume Fraction and Laminate Thickness How much fibre…? How much reinforcement? Weight fraction Used in manufacture. May refer to fibre or resin - 'GRP' manufacturers will specify a glass content of (e.g.) 25 wt%; a prepreg supplier might give a resin content of 34 wt%. Volume fraction Used in design to calculate composite properties. Almost always refers to fibre content. Weight fraction volume fraction conversion For the special case of a two-component composite (eg fibre and matrix): Wf / f Vf Wf / f (1 Wf ) / m fVf Wf fVf m (1 Vf ) fibre volume fraction Volume fraction - weight fraction conversion (epoxy resin matrix) 1 0.8 glass 0.6 HS carbon 0.4 aramid 0.2 0 0 0.2 0.4 0.6 fibre weight fraction 0.8 1 Maximum fibre volume fraction Theoretically, a unidirectional fibre composite could have Vf ≈ 90%. In practice, fibres cannot be perfectly aligned. Maximum volume fraction depends both on the fibre form and method of manufacture for a unidirectional fibre composite: Vf ≈ 60-70%. Maximum fibre volume fraction For other forms of reinforcement, maximum volume fraction also depends on the detailed arrangement of the fibres. The following values are typical: stitched ‘non-crimp’ woven fabric random (chopped strand mat) 0.6 0.4 - 0.55 0.15 - 0.25 How much fibre? Commercial reinforcements are characterised by their areal weight (Aw). This is simply the weight (usually given in g) of 1 m2 of the reinforcement. Aw depends on many factors fibre density, tow or bundle size, weave style, etc. Aw may range from 50 g/m2 or less (for lightweight surfacing tissues), up to more than 2000 g/m2 for some heavyweight non-crimp fabrics. Laminate thickness Two laminates, both containing 5 plies of reinforcement: fibre matrix high matrix content low matrix content low fibre content high fibre content = thick laminate = thin laminate Laminate thickness Fibre volume fraction is thus inversely proportional to laminate thickness. If the fibre content and laminate thickness are defined, we can calculate the fibre volume fraction: nAw Vf f d If the fibre content and volume fraction are defined, we can calculate the laminate thickness: nAw d fVf Ply thickness vs fibre volume fraction (glass) ply thickness (mm) 3 Area weight 2.5 200 g/m2 2 300 g/m2 1.5 450 g/m2 1 600 g/m2 0.5 0 0.1 0.2 0.3 0.4 0.5 fibre volume fraction 0.6 0.7 Ply thickness vs fibre volume fraction (HS carbon) ply thickness (mm) 1.6 Area weight 1.4 1.2 100 g/m2 1 150 g/m2 0.8 0.6 200 g/m2 0.4 0.2 500 g/m2 300 g/m2 0 0.2 0.3 0.4 0.5 0.6 fibre volume fraction 0.7 0.8 Example calculations 1. What will be the thickness of a laminate consisting of 2 layers of 450 g/m2 chopped strand mat if a resin to glass ratio (by weight) of 2:1 is used? 2. What fibre volume fraction is achieved if 3 layers of 800 g/m2 glass woven roving are compression-moulded to a thickness of 2 mm? Rules of Mixture for Elastic Properties 'Rules of Mixtures' are mathematical expressions which give some property of the composite in terms of the properties, quantity and arrangement of its constituents. They may be based on a number of simplifying assumptions, and their use in design should tempered with extreme caution! Density For the special case of a fibre-reinforced matrix: Vf f Vmm Vf f (1 Vf )m Vf (f m ) m since Vf + Vm = 1 Rule of mixtures density for glass/epoxy composites 3000 f 2500 kg/m 3 2000 1500 m 1000 500 0 0 0.2 0.4 0.6 fibre volume fraction 0.8 1 Micromechanical models for stiffness Unidirectional ply - longitudinal tensile modulus E1 = Ef Vf + Em ( 1-Vf ) Note the similarity to the rules of mixture expression for density. In polymer composites, Ef >> Em, so E1 Ef Vf This rule of mixtures is a good fit to experimental data (source: Hull, Introduction to Composite Materials, CUP) Generalised rule of mixtures for tensile modulus E = hL ho Ef Vf + Em (1-Vf ) hL is a length correction factor. Typically, hL 1 for fibres longer than about 10 mm. ho corrects for non-unidirectional reinforcement: ho unidirectional biaxial biaxial at 45o random (in-plane) random (3D) 1.0 0.5 0.25 0.375 0.2 60 50 40 UD 30 biaxial 20 CSM 10 0 0 0.2 0.4 0.6 0.8 fibre volume fraction Rule of mixtures tensile modulus (T300 carbon fibre) tensile modulus (GPa) tensile modulus (GPa) Rule of mixtures tensile modulus (glass fibre/polyester) 200 150 UD 100 biaxial quasi-isotropic 50 0 0 0.2 0.4 fibre volume fraction 0.6 0.8 Rule of mixtures elastic modulus glass fibre / epoxy resin 60 50 GPa 40 UD biaxial random 30 20 10 0 0.1 0.3 0.5 fibre volume fraction 0.7 GPa Rule of mixtures elastic modulus HS carbon / epoxy resin 180 160 140 120 100 80 60 40 20 0 UD biaxial UD quasi-isotropic UD plain woven 0.4 0.5 0.6 fibre volume fraction 0.7