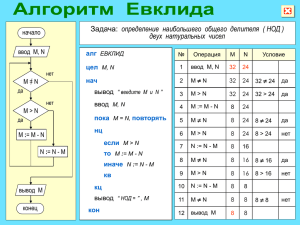
УПК 1г. 2четв КОНТРОЛЬНАЯ РАБОТА Тема ФОРМАТИРОВАНИЕ АБЗАЦА И ШРИФТЫ Вариант 1 Наберите текст и отформатируйте, как показано в образце используя элементы форматирования абзацев Задание 1 Элементы комбинаторики Размещения Размещениями из п элементов по к называются соединения, которые можно образовать из этих п элементов, собирая в каждое соединение по к элементов, при этом соединения могут отличаться друг от друга, как самими элементами, так и порядком их расположения. Например, из 3 элементов (а, b, с) по 2 можно образовать следующие размещения: ab, ас, ba, be, ca, cb. Число всех возможных размещений, которые можно образовать из п элементов по к, обозначается символом Akn и вычисляется по формуле: Akn = n(n-1)(n-2)...(n-k+1) Перестановки Перестановками из n элементов называются соединения, каждое из которых содержит все п элементов, отличающихся друг от друга только порядком расположения элементов. Например, из 3 элементов (а,Ь,с) можно образовать следующие перестановки: abc, hoc, cab, acb, bca, cba Число всех возможных перестановок, которые можно образовать из п элементов, обозначается символом Рn,и вычисляется по формуле: Рп=1*2*3*..*п = п! Сочетания Сочетаниями из п элементов по к называются соединения, которые можно образовать из этих n элементов, собирая в каждое соединение к элементов; при этом соединения отличаются друг от друга только самими элементами (различие порядка их расположения во внимание не принимается!. Например, из 3 элементов (а,b,с) по 2 можно образовать следующие сочетания: ab, ас, be. Число всех возможных сочетаний, которые молено образовать из п элементов по к, обозначается символом Сknи вычисляется по формуле: Сkn = Akn /Pk УПК 1г. 2четв Задание 2 КОНТРОЛЬНАЯ РАБОТА Тема ФОРМАТИРОВАНИЕ АБЗАЦА И ШРИФТЫ УЧЕБНЫЙ ЦЕНТР «СИРИУС» ул. Веселая, 15 г. Энский СВИДЕТЕЛЬСТВО Выдано Петрову Петру Петровичу в том, что в период с 1.09.10 по 30.10.10 он (а) проходил (а) обучение на компьютерных курсах в Учебном цитре «Сириус» и завершила изучение по следующим темам: -Операционная система WINDOWS XP – 4 (хорошо) -Текстовый редактор WORD 2007-5(отлично) -Табличный редактор EXEL 2007 – 4 (хорошо) Председатель квалификационной комиссии Рег. № 350 15.11.10 О.О. Дубов УПК 1г. 2четв КОНТРОЛЬНАЯ РАБОТА Тема ФОРМАТИРОВАНИЕ АБЗАЦА И ШРИФТЫ Вариант 2 Наберите текст и отформатируйте, как показано в образце используя элементы форматирования абзацев Задание 1 Происхождение слов «Алгебра» Мухаммад ибн Муса аль-Хорезми аль-Маджуси (787ок.850 гг.). Место рождения точно неизвестно. По одной из версий его предки, а возможно и он сам в юности, были магами, т.е. жрецами зороастрийской религии: «аль-Маджуси» означает «из рода магов (жрецов)». В зрелом возрасте попал в окружение калифа Ал-Ма`муна — сына калифа Харуна ар-Рашида. С 813 г. жил и работал в Багдаде. Краткая книга алмукабалы об исчислении алгебры и Эта книга заключает в себе название двух самых простых операций, необходимых для приведения уравнения к виду, когда в левой и правой частях стоят только положительные члены. (Ai-jabar) происходит от jabar обозначает исправление сломанного 11) сустава , т.е. перенесение отрицательного члена из одной части уравнения в другую. Название «алгебра и алмукабала» вскоре стало названием алгебры как науки. "Интерполяция" Interpolatio (лат.) — изменение, искажение; interpolo, interpolare (лат.) — 1) разглаживать, подновлять; 2) искажать, подделывать, фальсифицировать. Интерполяциями в римском праве назывались изменения, внесенные компиляторами при составлении Corpus juris civilis (529-534 гг.) в тексты различных авторов. Составители одни тексты пропускали, другие исправляли, нередко приписывая цитируемому юристу слова, которых он не мог сказать … Кстати, одна из статей кодекса называлась (О злодеях, математиках и прочих подобных) и предписывала: УПК 1г. 2четв КОНТРОЛЬНАЯ РАБОТА Тема ФОРМАТИРОВАНИЕ АБЗАЦА И ШРИФТЫ (Пусть изучение и упражнение в искусстве геометрии будет делом общественной важности) (Преступное же искусство математики безусловно воспрещается). Задание 2 Министерство общего и среднего образования 192281, Санкт-Петербург, Загребенский бульвар, 23 Тел: (812) 178-32-51 Факс: (812) 178-32-38 «___»_________________№__ ___на №___________от «___»_______ СПРАВКА Выдана _____________________________________________________ в том, что он (она) учится в ___________ классе Лицея информатики и компьютерной техники г. Санкт-Петербурга. Директор В. В. Курилов МП УПК 1г. 2четв КОНТРОЛЬНАЯ РАБОТА Тема ФОРМАТИРОВАНИЕ АБЗАЦА И ШРИФТЫ Вариант 3 Наберите текст и отформатируйте, как показано в образце используя элементы форматирования абзацев Задание 1 ИЗ ИСТОРИИ МАТЕМАТИКИ Евклид Евклид ( ) жил в III веке до н.э. в Александрии Египетской. Период правления Птолемея Сотера Основная заслуга Евклида состояла в систематизации знаний, полученных его предшественниками благодаря чрезвычайно логичному расположению выбранных предложений. В своей книге «Начала» ( в латинизированной форме — «Элементы») он изложил все, полученные к тому времени результаты планиметрии, стереометрии, теории чисел, исходя из немногих определений и аксиом. Однажды Птолемей спросил Евклида существует ли для изучения геометрии более краткий путь, чем его «Начала», на что получил ответ: В геометрии нет особых путей для государей. Наибольший общий делитель Наибольшим общим делителем (НОД) целых чисел a1, a2, …, an называется такой положительный общий делитель этих чисел, который делится на любой другой общий делитель этих чисел. Пример: НОД(21,15)=3; НОД(27,44)=1; НОД(120,66)=6. Алгоритм Евклида. Пусть и — положительные целые. Поделим B на A: , пусть остаток r1 не равен 0: . Поделим делитель на этот остаток: A=r1q2+ r2 , предположим, что остаток r2 A:B=Aq1+r1 не равен 0: . Снова разделим делитель на остаток и продолжим процесс далее до тех пор, пока на каком-то шаге не произойдет деление нацело, т.е. остаток будет равен нулю Пример: НОД(22, 8) = ? 22 = 8*2 + 6 (22, 8) = (8, 6) 8 = 6*1 + 2 (8, 6) = (6, 2) 6 = 2*2 + 2 (6, 2) = (2, 2) 2 = 2*1 + 0 УПК 1г. 2четв КОНТРОЛЬНАЯ РАБОТА Тема ФОРМАТИРОВАНИЕ АБЗАЦА И ШРИФТЫ Получили: НОД(22, 8) = 2. Задание 2 «БИЗНЕС-ЦЕНТР» 113244, г. Энск, Новая ул., 3 тел. 123-45-67 Заместителю директора ОДО «Веселый Роджер» Кулебякину В.Н. ул. Васина,11 22222, г. Эмск Уважаемый Василий Никифорович! Акционерное общество «Бизнес-Сервис» приглашает Вас 15 ноября 2008 г. В 20 часов на традиционное осеннее заседание Клуба энских джентльменов. Форма одежды - смокинг. Президент клуба А. М. Ростокин УПК 1г. 2четв КОНТРОЛЬНАЯ РАБОТА Тема ФОРМАТИРОВАНИЕ АБЗАЦА И ШРИФТЫ Вариант 4 Наберите текст и отформатируйте, как показано в образце используя элементы форматирования абзацев Задание 1 КОМБИНАТОРИКА Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Правила сложения и умножения в комбинаторике Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n+m способами. Пример 1. В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного? Решение Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек. По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами. Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n1 способами, второе действие n2 способами, третье – n3 способами и так до k-го действия, которое можно выполнить nk способами, то все k действий вместе могут быть выполнены: способами. Перестановки без повторений. Перестановки с повторениями Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предм етов на n различных местах? УПК 1г. 2четв КОНТРОЛЬНАЯ РАБОТА Тема ФОРМАТИРОВАНИЕ АБЗАЦА И ШРИФТЫ Задание 2 ОБЩЕСТВО С ДОПОЛНИТЕЛЬНОЙ ОТВЕТСТВЕННОСТЬЮ «КНИЖНЫЙ ДОМ» ул. Я. Коласа, 34, 220113, г. Минск тел./факс (017) 232 18 96 04.07.2006 № 4-9/131 на № _______ ад ____________ Директору ООО «Публицист» Перовичу В.Л. ул.Кропоткина, 57 220002, г.Минск-02 О проведении международной книжной выставки Уважаемый Вячеслав Леонидович! ОДО «Книжный дом» проводит 20-25 сентября 2019 г. в г.Минске традиционную международную выставку-продажу книг научного, учебного, методического, производственнопрактического и справочного характера. Так как Ваша фирма осуществляет выпуск литературы соответствующего профиля, приглашаем Вас принять участие в организуемой выставке. С уважением, Генеральный директор ОДО Г.М. Брегер УПК 1г. 2четв КОНТРОЛЬНАЯ РАБОТА Тема ФОРМАТИРОВАНИЕ АБЗАЦА И ШРИФТЫ УПК 1г. 2четв КОНТРОЛЬНАЯ РАБОТА Тема ФОРМАТИРОВАНИЕ АБЗАЦА И ШРИФТЫ Краткие теоретические сведения и примеры решения Наибольший общий делитель Наибольшим общим делителем (НОД) целых чисел a1, a2, …, an называется такой положительный общий делитель этих чисел, который делится на любой другой общий делитель этих чисел. Пример: НОД(21,15)=3; НОД(27,44)=1; НОД(120,66)=6. Алгоритм Евклида Используется для нахождения наибольшего общего делителя двух чисел. Идея: НОД(a, b) = НОД(b, r), где a = b·q + r. Пример: НОД(22, 8) = ? 22 = 8*2 + 6 (22, 8) = (8, 6) 8 = 6*1 + 2 (8, 6) = (6, 2) 6 = 2*2 + 2 (6, 2) = (2, 2) 2 = 2*1 + 0 Получили: НОД(22, 8) = 2. Простые числа Положительное целое не равное нулю число называется простым, если оно делится только на самого себя и на единицу. Примеры: 11 – простое; 29 – простое; 56 – составное (56 = 7 ∙ 4 ∙ 2). Два числа m и n называются взаимно простыми, если они не имеют общих делителей кроме единицы, то есть наибольший общий делитель НОД(m, n)=1. Функция Эйлера Функцией Эйлера ϕ(n ) ( n ≥1) называют число положительных целых чисел меньших n и взаимно простых с n. Если n – простое число, то ϕ(n)=n – 1. Пример: ϕ(31) =30. Если n=p·q, где p и q – простые числа, то ϕ(n)=(p–1)∙(q–1). Пример: ϕ(35) = ϕ(5) ∙ ϕ(7) = 4 ∙ 6 = 24. Обобщенный алгоритм вычисления функции Эйлера для произвольного числа n. Если n представить как произведение простых чисел в соответствующих степенях: n = p1a1 ⋅ p2a2 ⋅ p3a3 ⋅ ⋅ ⋅ prar (p1, p2, …, pr – простые), то ϕ(n)=n∙(1–1/ p1)∙(1–1/ p2)∙…∙(1–1/ pr). Пример: ϕ (2700) = ? 2700 можно представить как 22∙33∙52. УПК 1г. 2четв КОНТРОЛЬНАЯ РАБОТА Тема ФОРМАТИРОВАНИЕ АБЗАЦА И ШРИФТЫ Тогда ϕ(2700)=2700∙(1–1/2)∙(1–1/3)∙(1–1/5)=720. Теорема Эйлера Если n ≥ 0 – положительное целое число и (a, n)=1, где a – целое, то справедливо: aϕ(n)=1 mod n. Пример: 41126 = ? mod 127. НОД(41,127) = 1, ϕ (127) = 126, поэтому 41126 = 1 mod 127. Пример: 4336 = ? mod 377. НОД(336,377) = 1, 377 = 13∙29, 13 и 29 – простые числа, поэтому ϕ(377) = ϕ(13) ∙ ϕ(29) = 12∙28 = 336, поэтому 4336 = 1 mod 377. Взаимообратные числа Для числа n взаимообратным по модулю r называется такое число m, для которого выполняется: (n·m) mod r = 1, или n·m = 1 mod r. (1) Доказательство: по теореме Эйлера: nϕ(n)=1 mod r или 1 = nϕ(n) mod r. (2) Перемножив (1) и (2), получим: n·m = nϕ(n) mod r, разделив обе части на n, получим: m = nϕ(n)–1 mod r. Пример: Найти взаимообратное по модулю 7 для числа 4. 4∙m = 1 mod 7, m = 4ϕ(7)–1 mod 7= 45 mod 7 = 2. Проверка: 4∙2 mod 7 = 8 mod 7 =1. Принципы модулярной арифметики Модулярная арифметика основывается на следующем равенстве: (a*b) mod m = [(a mod m)*(b mod m)] mod m, (3) где * – любая из следующих операций: “+” (сложение); “–” (вычитание); “×” (умножение). Данное равенство говорит о том, что вычисление (a*b) mod m в мо-дулярной арифметике даёт тот же результат что и вычисление (a*b ) в обычной целочисленной арифметике с последующим взятием остатка от деления полученного результата на m (mod m). Пример: 7∙9 mod 5 =[(7 mod 5)∙(9 mod 5)] mod 5. Принципы модулярной арифметики также применимы к операции возведения в степень, поскольку возведение в степень эквивалентно многократному умножению. УПК 1г. 2четв КОНТРОЛЬНАЯ РАБОТА Тема ФОРМАТИРОВАНИЕ АБЗАЦА И ШРИФТЫ Пример: Рассмотрим выражение mod 7. Возведение 3 в степень 5 и затем взятие результата по модулю 7 может быть произведено следующим образом: 35 Поскольку 5 = 2 ∙ 2 + 1, то 35=32∙2+1=(32)2∙31. УПК 1г. 2четв КОНТРОЛЬНАЯ РАБОТА Тема ФОРМАТИРОВАНИЕ АБЗАЦА И ШРИФТЫ ЗАДАНИЕ 4 «БИЗНЕСЦЕНТР» 113244, Москва, Новая ул., 3 тел. 12345-67 Уважаемый Василий Никифорович! Акционерное общество «БизнесСервис» приглашает Вас 15 ноября 2008 г. В 20 часов на традиционное осеннее заседание Клуба московских джентльменов. Презид ент клуба А. М. Ростокин Задание 1 1 Войдите в редактор MS Word. Ознакомьтесь со стандартным окном редактора (строка главного меню и ее команды, панель инструментов и ее кнопки, служебные кнопки, функциональные клавиши). 2 Установите поля документа: верхнее – 2 см, нижнее – 1,5 см, левое – 2,5 см, правое – 1 см. 3 Введите предложенный текст. 4 Сохраните текст под своим оригинальным именем. УПК 1г. 2четв КОНТРОЛЬНАЯ РАБОТА Тема ФОРМАТИРОВАНИЕ АБЗАЦА И ШРИФТЫ 5 Закройте документ. 6 Откройте созданный текст для редактирования. 7 Визуально отредактируйте текст. 8 Сохраните отредактированный документ. 9 Закройте документ. Задание 2 1 Найдите в приведенном ниже тексте все случаи, когда пробелы были использованы не по назначению, и определите, какие настройки формата следовало бы здесь применить. 2 Наберите текст, исправляя неточности. 3 Сохраните текст под своим оригинальным именем. 4 Закройте документ. Задание 3 1 Наберите текст и отформатируйте, как показано в образце, исправляя ошибки. УПК 1г. 2четв КОНТРОЛЬНАЯ РАБОТА Тема ФОРМАТИРОВАНИЕ АБЗАЦА И ШРИФТЫ 2 Сохраните текст под своим оригинальным именем. 3 Закройте документ. 2 Выделите первый абзац и установите начертание букв полужирным, раз- мер букв – 16 пт, тип шрифта – Courier New. 3 Сделайте выравнивание текста по ширине. 4 Для красной строки установите отступ в 1,5 см. 5 Для каждого абзаца установите свой тип и цвет шрифта. 6 Перед и после второго абзаца сделайте интервалы в 24 пт. 7 Третий абзац уплотните 8 После третьего абзаца сделайте интервал в 18 пт. 9 Сохраните отформатированный документ. Задание 6 Создайте акт по приведенному ниже образцу. АКТ Проведения технического обслуживания и проверки внутренних пожарных кранов Комиссия в составе председателя________________________________________ и членов комиссии__________________________________________________________________ __________________________________________________________________________ ________________ УПК 1г. 2четв КОНТРОЛЬНАЯ РАБОТА Тема ФОРМАТИРОВАНИЕ АБЗАЦА И ШРИФТЫ в соответствии с п. 89 Правил пожарной безопасности в Российской Федерации ППБ 01-03 провела техническое обслуживание и проверку работоспособности внутренних пожарных кранов. Внутренние пожарные краны ПК-1-ПК-6 проверены на работоспособность путем пуска воды и признаны годными к дальнейшей эксплуатации. Пожарные рукава просушены, перекатаны на новую складку и присоединены к кранам и стволам. Председатель комиссии___________________________ Члены комиссии: __________________________ __________________________ __________________________ __________________________ __________________________ __________________________ __________________________ «___»_______________2014г. УПК 1г. 2четв КОНТРОЛЬНАЯ РАБОТА Тема ФОРМАТИРОВАНИЕ АБЗАЦА И ШРИФТЫ