KVOSP

Министерство Образования Республики Беларусь
Учреждение образования «Белорусский государственный
университет информатики и радиоэлектроники»
кафедра систем телекоммуникаций
Урядов В.Н., Лукашевич С.А.
ЭЛЕКТРОННЫЙ РЕСУРС УЧЕБНОЙ ДИСЦИПЛИНЫ
«КОМПОНЕНТЫ ВОЛОКОННО-ОПТИЧЕСКИХ
СИСТЕМ ПЕРЕДАЧИ»
Для студентов направлений специальности:
1-45 01 01-01 Инфокоммуникационные технологии (системы телекоммуникаций),
1-45 01 01-06 Инфокоммуникационные технологии (лазерные информационно-измерительные системы).
Минск БГУИР 2016
СОДЕРЖАНИЕ
СОКРАЩЕНИЯ И ОПРЕДЕЛЕНИЯ
АМ-ЧПБП – амплитудная модуляция с частичным подавлением боковой
полосы;
ВАХ – ватт-амперная характеристика;
ВОК – волоконно-оптический кабель;
ВОЛС – волоконно-оптическая линия связи;
ВОСП – волоконно-оптическая система передачи;
ИХ – импульсная характеристика;
КВОСП – компоненты волоконно-оптической системы передачи;
ЛД – лазерный диод;
ЛФД – лавинный фотодиод;
ОВ – оптическое волокно;
ОИС – оптическая интегральная схема;
ОКГ – оптический квантовый генератор;
ОУ – оптический узел;
ПАВ – поверхностно-акустическая волна;
ПХ – импульсная характеристика;
СИД – светоизлучающий диод;
ФД – фотодетектор;
ASE – Amplifier Spontaneous Emission – усиленная спонтанная эмиссия;
AWG – Array Wave Guides – массив волноводов;
EDFA – Erbium Doped Fiber Amplifier – оптический усилитель на волокне, легированном эрбием;
OT – Optical Transmitter – оптический передатчик;
xWDM – Wavelength Division Multiplexing – семейство технологий волнового (спектрального) мультиплексирования с разделением по длинам волн;
Делитель – элемент линейной сети, обеспечивающий деление энергии оптического сигнала на несколько направлений.
Затухание (а) – отношение мощностей (Р) оптического сигнала на входе
P1 или выходе P2 сети или ее элемента, выражаемое в децибелах и вычисляемое
по формуле
а=10lg Р1 /Р2.
Ответвитель (сплиттер) – элемент линейной сети, обеспечивающий ответвление части энергии оптического сигнала на одно или несколько направлений.
Оптический узел – совокупность технических средств и устройств, обеспечивающих сопряжение волоконно-оптических участков линейной сети.
Оптический усилитель – элемент линейной сети, обеспечивающий усиление оптических сигналов без демодуляции и регенерации.
4
ВВЕДЕНИЕ
В последние годы рост потребности в услугах связи для различных сфер
деятельности людей обусловил бурное развитие средств телекоммуникаций во
всех цивилизованных странах. Оптическое волокно (ОВ) оказалось именно той
средой передачи, которая смогла удовлетворить возрастающие потребности людей в обмене информацией. Оптическое волокно и волоконно-оптическая техника играют в современной связи определяющее значение, первое – как среда
для оптической цифровой передачи, вторая как набор средств, дающих возможность осуществления такой передачи.
Элементную базу современных волоконно-оптических линий связи
(ВОЛС) представляют волоконно-оптические кабели, передающие и приемные
оконечные устройства (модули), оптические соединители, разветвители, коммутаторы, изоляторы и пр. Именно из этих аппаратурных средств как из кубиков
создаются системы оптической связи с заданными параметрами. Но каждый из
названных элементов представляет собой сложное изделие оптики (оптоэлектронное или оптико-механическое изделие), являющееся частью волоконно-оптической системы передачи (ВОСП), которое может быть выделено как самостоятельное изделие с точки зрения требований к испытаниям, приемке, поставке и
эксплуатации, и предназначенное для выполнения одной или нескольких функций по формированию, передаче, распределению, преобразованию и обработке
оптического сигнал [1]. Специальным образом сформированная группа таких изделий и представляет собой компоненты волоконно-оптических систем передачи
(КВОСП).
В данном методическом пособии приведены базовые знания по оптическим элементам волоконно-оптических систем передачи. Основной целью является изучение фотодетекторов оптического излучения, пассивных компонентов
волоконно-оптических когерентных и некогерентных оптических систем, физических принципов работы модуляторов оптического излучения, оптических усилителей, применяемых в ВОСП.
5
1 ВОПРОСЫ ПОСТРОЕНИЯ ВОЛОКОННО-ОПТИЧЕСКИХ
СИСТЕМ ПЕРЕДАЧИ
1.1 Основные эффекты и законы теории света
Оптика – специальный раздел физики, которая занимается изучением природы света, закономерностей его испускания, распространения и взаимодействия с веществом. В физике все виды материи разделяётся по природе либо на
волны, либо на частицы. Обычно свет представляется в виде волн, а электроны
– в виде частиц. Однако современные физические исследования показали, что
чёткой границы между частицами и волнами не существует. Поведение, как частицы, так и волны может быть и корпускулярным, и волновым.
Частицы света называются фотонами. Фотоны представляют собой
квант, или пакет излучения, который является элементарной единицей излучения. Количество энергии, переносимое квантом, зависит от его частоты: большие
частоты соответствуют большему количеству энергии. Длинам волн фиолетового диапазона соответствует большее количество энергии, чем красному цвету,
так как фиолетовому диапазону соответствуют большие частоты. Энергия Е (в
ваттах), сосредоточенная в одном фотоне, равна:
E = hf,
(1.1)
где f – его частота и h – постоянная Планка, равная 6,63·10–34 Дж-сек (Джоуль-секунда). Из этого уравнения видно, что энергия фотона зависит только от
его частоты (или длины волны). Энергия фотона пропорциональна частоте.
Квант энергии света, заключённой в одном фотоне, равен hf.
Чем выше частота, тем большую энергию имеет квант.
Инфракрасный свет
(1013 Гц)
6,63  10–20 Дж-сек
Видимый свет
(1014 Гц)
6,63  10–19 Дж-сек
Ультрафиолетовый свет
(1015 Гц)
6,63  10–18 Дж-сек
Рентгеновские лучи
(1018 Гц)
6,63  10–15 Дж-сек
Видимая область спектра
300 км
1 кГц
30 м 3 м 30 см
Короткие
волны
Средние
волны
Длинные
СВЧ
волны
1 МГц
0,3 мм
3 мкм 0,3 мкм
Инфракрасный
диапазон
Микроволны
1 ГГц
1012 ГГц
Длина волны
в вакууме 0,3 нм
Ультрафиолетовый
диапазон
1015 ГГц
1018 ГГц
Рисунок 1.1 – Спектр электромагнитных колебаний
6
Фотон является частицей с нулевой массой покоя. Если он не движется, то
он не существует. В этом смысле фотон не является частицей, такой как материальный предмет. Он служит вместилищем энергии, но ведёт себя как частица.
В волоконной оптике свет рассматривают и как частицу, и как волну.
Обычно в зависимости от смысла используют либо одно, либо другое понятие.
Например, характеристики оптического волокна основаны на длине волны, и
свет рассматривается как волна. Для описания работы одномодового волокна
пригодна только волновая теория.
Поскольку корпускулы излучаются отдельными порциями (квантами),
здесь для описания работы многомодового волокна пригодна лучевая теория.
Кроме того, испускание света источником или его поглощение детектором также
лучше описываются теорией частиц.
Два гармонических колебания s1 и s 2 называются когерентными, если разd
Ф2 t   Ф1 t   0
ность их фаз не зависит от времени: dt
и Ф2 t   Ф1t   const .
Поскольку Ф2 t   Ф1t   2  1 t  2  1 , то циклические частоты ко-


герентных колебаний должны быть одинаковы, т. е. 2  1  . В любой момент
времени разность фаз когерентных колебаний равна разности их начальных фаз:
Ф2 t   Ф1t   2  1 . Соответственно результирующие колебания – гармонические с той же циклической частотой .
Источники когерентных волн называются когерентными источниками.
Синусоидальные волны, частоты которых одинаковы, когерентны всегда. Гармонические колебания, частоты которых различны (ω1 ≠ ω2) некогерентны.
Однако следует помнить, что два гармонических колебания с различными
циклическими частотами ω1 и ω2 можно приближённо считать когерентными
лишь в течение промежутка времени t , за который разность фаз этих колебаний изменяется незначительно (Δt << τког).
Время когерентности рассматриваемых колебаний рассчитывается по формуле:
 ког 
2
.
2  1
(1.2)
Интерференцией волн называется явление наложения волн, при котором
происходит устойчивое во времени их взаимное усиление в одних точках пространства и ослабление в других в зависимости от отношения между фазами этих
волн. Интерферировать могут только когерентные волны, которым соответствуют колебания, совершающиеся вдоль одного и того же или близких направлений.
Под дифракцией света понимают огибание светом встречных препятствий, т. е. отклонение от законов геометрической оптики.
7
Поглощением света называется явление уменьшения энергии световой
волны при её распространении в веществе, происходящее вследствие преобразования энергии волны во внутреннюю энергию вещества или в энергию вторичного излучения, имеющего другой спектральный состав и иные направления распространения (например, фотолюминесценция). Поглощение света может вызвать нагревание вещества, возбуждение и ионизацию атомов или молекул и др.
Поглощение света описывается законом Бугера – Ламберта (закон Бугера), согласно которому интенсивность I плоской волны монохроматического
света уменьшается по мере прохождения через поглощающую среду по экспоненциальному закону:
I  I 0 e ax.
(1.3)
Здесь I 0 и I – значения интенсивности света на входе и выходе из слоя
среды толщиной x, а a – натуральный показатель преломления среды, который
зависит от химической природы и состояния поглощающей среды и от длины
волны света λ.
Рассеянием света называется явление преобразования света веществом,
сопровождающееся изменением направления распространения света. Рассеяние
света происходит в оптически неоднородной среде, показатель преломления которой нерегулярно изменяется от точки к точке вследствие флуктуаций плотности среды (рэлеевское рассеяние) либо за счёт присутствия в среде инородных
малых частиц, т. к. во всех типах стёкол, как правило, имеются примеси (такие,
как окислы металлов, ионы переходного металла), размеры которых гораздо
меньше, чем длина волны. В первом случае рассеяние света называется молекулярным рассеянием, а во втором – рассеянием света в мутной среде.
Количество рассеиваемой энергии зависит от плотности расположения дефектов.
Молекулярное рассеяние света в чистых средах, не содержащих инородных
примесей, обусловлено неоднородностями, которые возникают в процессе беспорядочного теплового движения частиц среды. Эти неоднородности связаны с
флуктуациями плотности, а в средах с анизотропными (полярными) молекулами
– также с флуктуациями ориентации этих молекул. Среда называется изотропной, если её физические свойства, существенные в рассматриваемых задачах,
одинаковы во всех направлениях.
В соответствии с законом Рэлея интенсивность рассеяния обратно пропор-
 
4
циональна длине волны в четвёртой степени  . Поэтому она быстро уменьшается по мере роста длины волны.
Дисперсией света называется зависимость фазовой скорости vф света от
его частоты f. Существование дисперсии света в среде обусловлено тем, что её
показатель преломления n зависит то частоты f.
8
1.2 Распространение световых лучей в оптических волокнах
Как правило, гармоническая волна имеет неплоские волновые поверхности. На каждом малом участке волновую поверхность можно заменить частью
плоскости, касательную к ней в рассматриваемой точке.
grad S
n
Пучок локально
параллельных
световых лучей.
Рисунок 1.2 – Волновой фронт световых лучей
В результате приходим к теории световых лучей, направленных по нормали
к волновым поверхностям, то есть к геометрической оптике. Величиной grad S
определяется световой луч в каждой точке волновой поверхности.
Нужно хорошо усвоить, что физический смысл плоской волны и физический смысл световых лучей (иначе говоря, геометрической оптики) один и тот
же.
Законы геометрической оптики используются для описания и анализа процесса передачи оптических сигналов, когда длина волны излучения  значительно меньше размеров диаметра сердцевины оптического волокна, то есть 
<< 2R, где R – радиус сердцевины.
В геометрической оптике световые волны изображаются световыми лучами, которые распространяются в однородной среде прямолинейно.
При попадании на границу раздела двух сред с разными значениями показателей преломления световой луч изменяет своё направление и в общем случае появляется преломленный и отражённый лучи.
Показатель преломления, обозначаемый n, является безразмерной величиной, выражаемый через отношение скорости света в вакууме (с) к скорости света
а материале (v):
c
n 
v
(1.4)
Среда, у которой показатель преломления больше, называется оптически более плотной, в противном случае – менее плотной.
9
п
отр
пп
n1
п
п
n2
n1 n2
пр
кр
п - угол падения;
отр – угол отражения;
пр – угол преломления.
п = отр
пр  п
Свет отклоняется от перпендикуляра
кр- критический угол
n1
Луч не попадает во второй материал
n2
900
п
n1
n2
отр
п = отр. Угол падения равен углу
отражения.
Если угол падения больше критического, то свет будет отражён от границы
двух сред
Рисунок 1.3 – Законы преломления и отражения
Соотношения между углами падения п, отражения отр и преломления
пр определяются законом Снеллиуса:
п = отр и n1 Sin п = n2 Sin пр
(1.5)
Sinn n2
  n21,
Sin

n1
пр
или
если n1  n2, то пр  п.
Путём увеличения угла падения можно достичь состояния, при котором
преломленный луч будет скользить по границе раздела сред, не переходя в другую среду, т. е. пр= /2. Угол падения, при котором имеет место данный эффект,
называется критическим углом кр полного внутреннего отражения
кр  arc sin
n2
n1
(1.6)
Очевидно, что для всех углов падения, больших критического ( п  кр),
10
будут иметь место только отражения, а преломления будут отсутствовать. Это
явление называется полным внутренним отражением. На этом эффекте основан
принцип передачи оптического излучения по оптическим волноводам.
Даже когда свет проходит в более плотную среду, некоторая его часть отражается назад в исходную среду. Этот эффект получил название отражение
Френеля. Чем больше разница показателей преломления сред, тем больше доля
света отражается назад. Показатель Френелевского отражения F на границе с
воздухом равен:
2
 n 1
F 
.
 n  1
В децибелах потери переданного света составляют:
(1.7)
дБ = -10 log (1-F).
Для света, падающего из воздуха на границу стекла (n = 1,5 для стекла),
Френелевское отражение равно примерно 0,17 дБ. Поскольку такого рода потери
происходят как при вхождении света в стекло, так и при выходе из него, то потери на соединении двух стёкол составляют 0,34 дБ. Френелевское отражение не
зависит от направления прохождения двух сред.
1.3 Типовая конструкция оптического волокна
В общем случае оптическое волокно (ОВ) состоит из сердцевины
(рис. 1.4), по которой происходит распространение световых волн, и оболочки,
предназначенной, с одной стороны, для создания лучших условий отражения на
границе раздела "сердцевина – оболочка", а с другой – для снижения излучения
энергии в окружающее пространство. С целью повышения прочности и тем самым надежности волокна поверх оболочки, как правило, накладывается первичное защитное упрочняющее покрытие. Такая конструкция ОВ является типовой
и используется во многих ОВ в качестве базовой.
6
5
4
3
2 1
Рисунок 1.4 – Общий вид типового ОВ: 1-сердцевина, 2-оболочка, 3-силиконовое покрытие, 4-буферная оболочка, 5-упрачняющая оболочка, 6-внешняя оболочка
11
Рабочая оболочка предназначена:
а) для создания лучших условий отражения на границе раздела «сердцевина-оболочка;
б) для снижения излучения энергии в окружающее пространство.
Причём n1 > n2, где n1 – показатель преломления сердцевины и n2 – показатель преломления оболочки.
Для характеристики волокна используются соотношения, которые принято
называть разностью показателей преломления и относительной разностью показателей преломления.
Разность показателей преломления сердцевины n1 и оболочки n2 для многоволнового оптического волокна типовое значение порядка 0,01 и менее 0,004
для одномодового волокна. Обозначается Δn и вычисляется по формуле:
 n  n1  n2 .
Под относительной разностью показателей преломления Δ понимают величину, равную, отношению разности показателей преломления сердцевины и
2
2
2
оболочки к показателю преломления сердцевины:   n1  n2 2n1  n1  n2  n1 ,


2
3
и которое для большинства ОВ равно   10 ...10 .
Показатель преломления оболочки имеет постоянное значение, а показатель преломления сердцевины может быть либо постоянным, либо изменяться
вдоль радиуса по определённому закону. Характер изменения показателя преломления ОВ вдоль радиуса называется профилем (индексом) показателя преломления.
Показатель преломления оптической оболочки менее чем на один процент
меньше показателя преломления сердцевины. Характерные величины показателей преломления n1=1,47 и n2=1,46. Производители волокна строго контролируют разность показателей для получения нужных характеристик ОВ.
Например, показатель преломления сердцевины оптического волокна
фирмы Fujikura составляет n1 =1,465, фирмы Corning – n1 = 1,4681. Разность показателей преломления для многомодовых волокон Δ = n1 - n2 → 0,01; для одномодовых - Δ = n1 - n2 → 0,004.
Волокна, удовлетворяющие условию n1  n2 << n1 , относятся к слабо
направляющим волокнам.
Специфические особенности движения света вдоль волокна зависят от
многих факторов:
1. Размера волокна.
2. Состава волокна.
3. Процесса инжекции света внутрь волокна.
Волокна сами по себе имеют чрезвычайно малый диаметр. Наиболее распространённые типы волокон имеют следующие размеры:
Сердцевина (мкм)
Оболочка (мкм)
8
125
50
125
12
62,5
125
Оптические волокна характеризуются по двум параметрам.
Первый – по материалу, из которого сделано волокно:
 Стеклянные волокна имеют как стеклянную сердцевину, так и стеклянную оптическую оболочку. Стекло, используемое в данном типе волокна, состоит из сверхчистого сверхпрозрачного диоксида кремния или плавленого
кварца. В стекло добавляют примеси, чтобы получить требуемый показатель
преломления. Германий и фосфор увеличивают n, бор и фтор уменьшают его.
В стекле присутствуют другие примеси, не извлечённые в процессе
очистки. Из-за них увеличивается затухание, обусловленное рассеянием и поглощением света.
 Стеклянные волокна с пластмассовой оболочкой (PCS) имеют характеристики хуже, чем у полностью стеклянных.
 Пластические волокна имеют пластиковые сердцевину и оболочку.
Имеют повышенное затухание и более узкую полосу пропускания. Пластиковые
волокна самые дешёвые и обладают электромагнитной невосприимчивостью.
Второй – по индексу преломления сердцевины и модовой структуре света:
n2
- многомодовый ступенчатый индекс;
n1
n2
n2
- одномодовый ступенчатый индекс;
n1
n2
n2
- многомодовый градиентный индекс.
n(r)
n2
Существует два основных вида профиля: ступенчатый и сглаженный
(градиентный). В случае сглаженного профиля показатель преломления сердцевины не является однородным: показатель максимален в центре и постепенно
спадает вплоть до оптической оболочки. Показатель преломления сердцевины
меняется вдоль радиуса по закону показательной функции:

n(r )  n1 1  2(r / R)q

(1.8)
где r – текущий радиус; R – радиус сердцевины; n1 – показатель преломления в
центре сердцевины, равный примерно 1,5; q = {1,∞} – показатель степени, определяющий изменение n(r ) ;  =0.003 – 0.01.
При q = 2 – волокну с наиболее распространенным параболическим профилем показателя преломления, для которого
13

n(r )  n1 1  2(r / R)2

(1.9)
Очевидно, что при q = ∞ профиль показателя преломления определяется
как
 n при r  R;
n( r )   1
n2 при r  R;
(1.10)
и соответствует ступенчатому волокну. На рисунке 1.5 показан характер
изменения показателя преломления сердцевины при разных значениях q.
q=4
q=∞
q=2
n2
n(r)
n2
Рисунок 1.5 – Изменение показателя преломления
Выбор соотношения между n1 и n2 определяется различными факторами в
зависимости от назначения и области применения ОВ. Кроме того, ступенчатые
ОВ могут иметь и несколько отражающих оболочек, например, так называемое
волокно W – типа, с сердцевиной из материала с показателем преломления n1
окруженной двумя оболочками, первая из которых имеет показатель преломления n2 , а вторая n3 , причем n1 > n2 > n3 . Диаметр внутренней оболочки равен 2R
≈ 15 мкм.
1.4 Основы лучевой теории распространения света в ОВ
Как было отмечено выше, лучи света распространяются в ОВ при выполнении условий n1  n2 , в связи с чем для характеристики волокна используется
соотношение, которое принято характеризовать относительной разностью пока2
2
2
зателей преломления   (n1  n2 ) / 2n1 и, и которое для большинства ОВ равно
  102...103 .
Процесс распространения световых лучей в ОВ осуществляется в рамках
геометрической оптики (рис. 1.6).
14
СИ
n2
ΘA
2ΘA
Θпр
R
СВ
ΘКР
n1
А
φm
В
Вн
СВ
n2
С
n0=1
n1 > n2 > n0
Рисунок 1.6 – Распространение излучения по ступенчатому
и градиентному многомодовым и одномодовому ОВ
При попадании светового излучения на торец ОВ с радиусом R в нём могут
распространяться три типа световых лучей: направляющие, вытекающие (оболочечные) и излучаемые. Наличие и преобладание какого-либо лучей определяется
углом их падения на границу раздела "сердцевина – оболочка". Очевидно, что
при некотором угле падения лучей на торец волокна, угле ввода ΘВ оптического
излучения в ОВ и их дальнейшее попадание на границу раздела на ней может
иметь место полное внутреннее отражение. Те лучи, которые падают на границу
раздела под углом Θ ≥ ΘКР (лучи А, В) распространяются в ней, не претерпевая
преломления. Эти лучи называются направляемыми (ВН), и они являются основным типом лучей в сердцевине ОВ.
Лучи, падающие на границу раздела под углом Θ < ΘКР (луч С), носят
название вытекающих лучей (лучей оболочки) (СВ). Те лучи, которые излучаются из оболочки в окружающее пространство (лучи СИ), носят название излучаемых лучей. Они, естественно, не распространяются вдоль ОВ, а, как правило,
возникают в местах нерегулярностей волокна. При критическом угле падения
угол преломления Θпр=  /2, поэтому будем иметь равенство:
n1  Sinк  n2
(1.11)
При угле падения Θ > ΘКР имеет место явление полного внутреннего отражения. Для выполнения этого условия необходимо, чтобы угол наклона луча к
оптической оси волокна φ = π/2 – Θ был меньше φm = π/2 – ΘK, а угол падения ΘВ
луча на торец волокна был меньше некоторой величины ΘА. Для определения
углов ΘA и φm воспользуемся законом Снеллиуса, приняв n0=1 (показатель преломления воздуха).
SinВ  n1Sin  n1Cos.
(1.12)
15
При угле падения, равном критическому
Sin A  n1Sinm  n1CosКР .
(1.13)
Выразим Sin A через показатели преломления сердцевины и оболочки
n1Sin КР  n2 ,
Cos КР
n12  n22

.
n1
Sin A  n12  n22 .
(1.14)
(1.15)
Очевидно, что излучаемые и вытекающие волны – это паразитные волны,
приводящие к рассеиванию энергии и искажению информационного сигнала.
1.5 Апертура оптического волокна
Как следует из вышеизложенного, существует бесконечное множество лучей, которые, будучи введенными в ОВ под углом В   A , в дальнейшем, при
распространении по волокну, имеют n  кр . Следовательно, для обеспечения
условия полного внутреннего отражения при распространении световых лучей
необходимо обеспечить ввод излучения в торец ОВ под углом, меньшим или равным  A .
Угол  A между оптической осью и одной из образующих светового конуса
– лучей, падающих в торец ОВ (рис. 1.6), для которых в дальнейшем выполняется
условие полного внутреннего отражения, носит название апертура ОВ. Физически апертура характеризует эффективность ввода оптического излучения в ОВ,
а для ее числовой оценки используется понятие номинальной числовой апертуры
(Numerical Aperture), значение которой для ступенчатого оптического волокна
определяется выражением
NA  n0  sin  A ,
(1.16)
где n0 – показатель преломления окружающей среды, равный для воздуха
n0 =1.
В соответствии с законом Снеллиуса можно записать
n0 sin  A  n1 sin( / 2  КР ),
и, учитывая, что
16
(1.17)
КР  arcsin(n2 / n1 ),
(1.18)
выражение для номинальной числовой апертуры примет вид
NA  n1  n2 n1 2 .
2
2
(1.19)
Из последнего выражения видно, что с увеличением разности показателей
преломления сердцевины и оболочки значение NA возрастает и, следовательно,
улучшается эффективность ввода излучения в ОВ. Например, при n1 =1.51 и n2
=1.13 все меридианные лучи, падающие из воздуха на торец ОВ, входят в сердцевину (NA=1,  A   / 2 ).
Последнее выражение учитывает только меридианные лучи, в то время как
в ОВ в основном имеют место косые лучи с гораздо более сложной траекторией
распространения, расчет ввода которых гораздо сложнее. Поэтому получить простое выражение для числовой апертуры косых лучей не удается. Однако здесь
необходимо отметить, что апертура, полученная по данному выражению для меридианных лучей ступенчатого ОВ, меньше действительной апертуры, учитывающей все введенные лучи.
Для градиентных ОВ вводится понятие локальной числовой апертуры, равной
NA(r )  n1 (r )  n2 ,
2
2
(1.20)
которая показывает, что максимальный угол ввода оптического излучения
в этом случае определяется тем, в какой точке сердцевины волокна находится
вершина конуса, иными словами, захват волокном вводимого луча света зависит
от того, в какой точке сердцевины он вводится в градиентное волокно. Очевидно,
что при r = 0, т. е. при вводе излучения по оси волокна, локальная числовая апертура равна номинальной числовой апертуре. Для наиболее распространенного
градиентного ОВ с параболическим профилем показателя преломления числовая
апертура определяется выражением
NA 
1
2
2
n1  n2 .
2
(1.21)
Естественно, что определение числовой апертуры косых лучей градиентного волокна представляет еще более сложную задачу, нежели в случае ступенчатого.
В заключение следует отметить, что равенство числовых апертур источника и приемника излучения является одним из необходимых условий достижения малых потерь при их соединении.
17
1.6 Затухание в волоконных световодах
Затухание в волоконном световоде возникает вследствие поглощения, рассеяние и потерь связанных с микроизгибами. Типичная характеристика затухания кварцевого оптического волокна и ее эволюция с развитием технологии производства волокон представлена на рисунке 1.7.
Реальная характеристика
затухания
α, дБ/км
Восьмидесятые годы
с 2000г производство
волокон ZWP
10.0
Релеевское
рассеяние
потери ~ 1/λ4
0,1
0,8
1,0
Окно
прозрачности 3
ОН -
Окно
прозрачности 2
1.0
Окно прозрачности 1
Физические ограничения
оптического волокна
1,2
Инфракрасное
поглощение
1,4
1,6
1,8
λ, мкм
Рисунок 1.7 – Затухание оптического волокна в зависимости от длины
волны (показаны три окна прозрачности, используемые для ВОСП)
К фундаментальным факторам потерь относятся механизмы поглощения и
рассеяния. Основной вклад вносят потери за счет релеевского рассеяния и инфракрасного поглощения. До недавнего времени существенный вклад вносили потери, обусловленные поглощением на примесях – в основном на примесях гидроксильной группы ОН–. Эти потери носят резонансный характер. Дополнительные факторы потерь в оптических волокнах – это потери, вызванные микро- и
макроизгибами волокна, потери, обусловленные флюктуациями диаметра сердцевины волокна (границы сердцевина-оболочка). Эти потери нередко называют
кабельными.
Как показывает рисунке 1.7 в области малых длин волн затухание кварцевого оптического волокна уменьшается с увеличением длины волны в основном
по закону Релеевского рассеяния. Релеевское рассеяние обусловлено флюктуациями показателя преломления материала сердцевины вдоль и поперек оси волокна, что приводит к рассеянию света на случайных изменениях показателя преломления. Часть рассеянного светового потока образует поток обратного релеевского рассеяния, распространяющийся к источнику излучения, часть - попутный поток, направление распространения которого совпадает с направлением
18
распространения полезного сигнала, а часть уходит в оболочку. Потери за счет
релеевского рассеяния изменяются по закону
 PP 
CPP
4 ,
(1.22)
где  – длина волны, мкм; CPP – постоянная, которая зависит от состава
материала сердцевины волокна и лежит в пределах CPP=0,7…0,9 мкм4дБ/км.
В области длин волн более 1,7 – 1,8 мкм начинают проявляться потери изза инфракрасного поглощения в кварце, вызванного резонансами атомов в кристаллической решетке SiO2. Изменение затухания инфракрасного поглощения
описывается формулой:
 k

 ИКП  СИКП  exp  ИКП 
(1.23)
 ,

где СИКП и kИКП – постоянные коэффициенты, которые для чистого кварца
составляют порядка СИКП=0,9 дБ/км, kИКП=0,8 мкм.
Поглощения на примесях связаны с резонансами материала примеси. В
частности, поглощением на примеси гидроксильной группы OH–- определяются
пики потерь в областях длин волн 1383; 1240; 1130; 950; 875; 825 и 725 нм. Этот
тип потерь зависит от технологии изготовления волокна. С разработкой более
совершенных методов очистки материала кварцевого стекла от примесей и способов защиты от формирования примесей гидроксильной группы в стекле в дальнейшем были получены оптические волокна с пониженным водяным пиком
(LPW – low water peak) или, как их еще называют, волокна с нулевым водяным
пиком (ZWP –zero water peak). К волокнам этой группы относятся волокна AllWave (OFS) и SMF-28e (Corning). Потери для таких волокон на «водяном» пике
уменьшены до 0,31 дБ/км.
Фундаментальные механизмы потерь определяют область минимального
затухания и теоретический предел минимума потерь кварцевого волокна, который составляет около 0,15 дБ/км на длине волны 1550 нм. Однако достичь этого
предела не позволяют кабельные потери из-за микро- и макроизгибов волокна,
флюктуаций его геометрических характеристик.
Диапазон работы ВОСП выбирается в области минимального затухания
кварцевых оптических волокон и лежит в пределах 1260 -1675 нм. Выделяют
шесть спектральных диапазонов, данные которых сведены в таблице 1.1.
Таблица 1.1
Условное
обозначение
O
E
S
C
Наименование
Основной (original)
Расширенный (expanded)
Коротковолновый (short )
Стандартный (conventional)
Диапазон,
нм
1260–1360
1360–1460
1460–1530
1530–1565
19
L
U
Длинноволновый (long)
Сверх-длинноволновый (ultra-long)
1565–1625
1625–1675
Сегодня на местных сетях в основном работают в диапазоне O, а на магистральных в диапазонах C и L, где можно использовать оптические усилители на
легированных эрбием волокнах EDFA (erbium doped fiber amplifier). Однако в
последние годы с внедрением систем «грубого» спектрального уплотнения
(CWDM) начинают осваиваться все диапазоны.
1.7 Дисперсия оптического волокна
Другим важным параметром оптического волокна является дисперсия, которая определяет его пропускную способность для передачи информации.
Дисперсия – это рассеивание во времени спектральных или модовых составляющих оптического сигнала, которое приводит к увеличению длительности
импульса оптического излучения при распространении его по ОВ (рис. 1.8) и
определяется разностью квадратов длительностей импульсов на выходе и входе
ОВ [2]:
   в ых2   в х2 ,
(1.24)
где значения  в ых и  в х определяются на уровне половины амплитуды импульсов.
импульс
на входе
самый быстрый и медленный лучи
импульс
на выходе
n2
n1
n2
Ступенчатое многомодовое волокно
n2
n(r)
n2
Градиентное волокно
n2
n1
Одномодовое волокно
20
n2
Рисунок 1.8 – Распространение излучения по ступенчатому
и градиентному многомодовым и одномодовым ОВ
Дисперсия не только ограничивает частотный диапазон ОВ, но существенно снижает дальность передачи сигналов, так как чем длиннее линия, тем
больше увеличение длительности импульсов.
Дисперсия в общем случае определяется тремя основными факторами: различием скоростей распространения направляемых мод, направляющими свойствами оптического волокна и параметрами материала, из которого оно изготовлено. В связи с этим основными причинами возникновения дисперсии являются,
с одной стороны, большое число мод в ОВ (межмодовая дисперсия), а с другой
стороны – некогерентность источников излучения, реально работающих в спектре длин волн  (хроматическая дисперсия). Межмодовая дисперсия преобладает в многомодовых ОВ и обусловлена отличием времени прохождения мод по
ОВ от его входа до выхода. Для ОВ со ступенчатым профилем показателя преломления скорость распространения электромагнитных волн с длиной волны 
одинакова и равна v  c  l  n1, где c – скорость света, а l – длина волокна. Как
было показано выше, в этом случае все лучи, падающие на торец ОВ под углами
к его оси в пределах 0     A , достигают приемного устройства с некоторым
временным сдвигом, что, естественно, приводит к увеличению длительности
принимаемого импульса.
Межмодовая дисперсия градиентных ОВ, как правило, на порядок и более
ниже, чем у ступенчатых волокон. Это обусловлено тем, что за счет уменьшения
показателя преломления от оси ОВ к оболочке скорость распространения лучей
вдоль их траекторий изменяется – так, на траекториях, близких к оси, она
меньше, а удаленных – естественно, больше. Следовательно, лучи, распространяющиеся кратчайшими траекториями (ближе к оси), обладают меньшей скоростью, а лучи, распространяющиеся по более протяженным траекториям, имеют
большую скорость. В результате время распространения лучей выравнивается и
увеличение длительности импульса становится меньше. Так как межмодовая
дисперсия не зависит от характеристик источника излучения, для многомодовых
волокон ее оценивают по полосе пропускания ОВ ( МГц  км ).
Согласно геометрической интерпретации распространения оптических
лучей по ОВ, время распространения луча зависит от угла  n и, как было показано выше, определяется выражением
tg (n )  L  n1 / c  cosn .
Так как минимальное время распространения оптического луча имеет место при n  0 , а максимальное при n  КР , соответствующие им значения
времени распространения можно записать как
21
 м ин  L  n / c и t м акс  L  n1 / c  cosкр ,
откуда значение межмодовой дисперсии равно
L
c
 м м  t м акс  t м ин  n1
(n1  n2 ) n1

L
n1
c .
(1.25)
Из последнего выражения следует, что межмодовая дисперсия возрастает
с увеличением длины волокна. Однако это справедливо только для идеального
волокна, в котором взаимодействие между модами отсутствует. В реальных
условиях наличие неоднородностей, кручение и изгиб волокна приводят к постоянным переходам энергии из одних мод в другие – взаимодействию мод, в связи
с чем дисперсия становится пропорциональной L . Это явление проявляется не
сразу, а после определенного расстояния прохождения световой волны, которое
носит название длины установившейся связи мод. Это значение принимается
равным 5 - 7 км для ступенчатого волокна и 10 - 15 км – для градиентного и
установлено эмпирическим путем.
В градиентных многомодовых волокнах время распространения оптических лучей, как было показано выше, определяется законом изменения показателя преломления и при определенных условиях выравнивается, что, естественно, влечет к уменьшению дисперсии. Так, при параболическом профиле показателя преломления q=2 значение межмодовой дисперсии будет определяться
выражением
L 2
 мм 
n1
c 2 ,
(1.26)
а при qопт  2(1  2) она достигает минимального значения, равного
L 2
 мм 
n1
c 8 .
(1.27)
Отличие времени распространения каждой из направляемых мод, образующих сигнал, от частоты спектра источника оптического излучения приводит к
возникновению так называемой хроматической (частотной) дисперсии, которая,
в свою очередь, складывается из внутримодовой (волноводной) дисперсии и материальной дисперсии.
Первый тип дисперсии обусловлен направляющими свойствами сердцевины ОВ, а именно зависимостью групповой скорости моды от длины волны оптического излучения, что приводит к различию скоростей распространения частотных составляющих излучаемого спектра. Поэтому внутримодовая диспер-
22
сия в первую очередь определяется профилем показателя преломления ОВ и про ,
порциональна
ширине
спектра
излучения
источника
т.е.
 в    L  M ( ) ,
(1.28)
где M ( ) – удельная внутримодовая дисперсия.
Второй тип дисперсии вызван зависимостью показателя преломления
сердцевины от длины волны n1 ( ) , что, как и в предыдущем случае, приводит к
различным скоростям распространения спектральных составляющих источника
излучения. Возникающая при этом различная задержка частотных составляющих распространяющегося в ОВ излучения определяет дисперсию материала,
которая равна
L d 2n1 ( )
 м ат    L  M ( ) 

c
d2
.
(1.29)
Здесь следует отметить, что материальная дисперсия кварцевого ОВ при
определенной частоте имеет нулевое значение, так как при длине волны  =1,28
мкм она изменяет свой знак. Эта точка носит название точки нулевой материальной дисперсии. Очевидно, что, изменяя соотношение между модовой и материальной дисперсией, точку нулевой дисперсии можно перемещать в небольших
пределах (рис. 1.9). В общем виде дисперсия на участке волокна длиной  будет
равна
   м м2   хр 2   м м2  ( в   м ат)2 ,
(1.30)
где  м м и  хр   в   м ат – расширение импульса на выходе ОВ относительно импульса, поданного на его вход, имеющее место в результате межмодовой и
хроматической дисперсии соответственно.
23
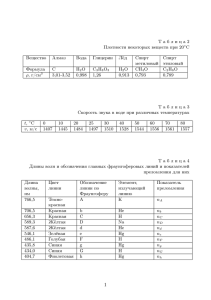
Рисунок 1.9 – Зависимость материальной, волноводной, результирующей дисперсии от длины волны
В нормальных условиях материальная дисперсия преобладает над волноводной, причем обе ее составляющие могут иметь противоположный знак и различаться характером зависимости от длины волны. В ряде случаев это позволяет
оптимизировать профиль показателя преломления волокна путем минимизации
суммарной дисперсии на определенной длине волны за счет взаимной компенсации материальной и волноводной дисперсии. Известно, что для кварцевых ОВ
минимум затухания соответствует длине волны 1,55 мкм и при больших скоростях передачи дальность связи на этой длине волны может ограничиваться дисперсией, поэтому для ее снижения осуществляется выбор соответствующего
профиля показателя преломления ОВ. Так как хроматическая дисперсия зависит
от длины световой волны и, следовательно, от ширины спектра источника оптического излучения, она нормируется в nc /(нм  км).
В качестве примера на рис. 1.10 представлены зависимости хроматической
дисперсии и ее составляющих от длины волны для различных типов профиля
показателя преломления одномодовых ОВ. Как следует из данного рисунка,
обычное одномодовое волокно не обеспечивает малой дисперсии для  =1,55
24
мкм, поэтому были разработаны ОВ со смещенной (Dispersion Shifted) или сглаженной (Dispersion Flattened) дисперсией, которые отличаются конфигурацией
профиля показателя преломления. В результате исследований волокон со смещенной дисперсией было показано, что наилучшие показатели обеспечивают волокна с треугольным профилем, так как они обладают самофокусирующими
свойствами и удерживают распространяющиеся лучи в небольшом объеме, прилегающем к оси ОВ.
25
Рисунок 1.10 – Зависимость дисперсии от длины волны оптического
излучения одномодовых ОВ
Так как оптические волокна со смещенной дисперсией обеспечивают минимальную дисперсию только на одной длине волны, это затрудняет применение
мультиплексирования для работы на нескольких оптических несущих в окне
прозрачности ОВ. Поэтому с целью минимизации дисперсии во всем окне прозрачности используют волокна со сглаженной дисперсией, которые также выполняются с различными профилями показателей преломления.
Существует множество типов профилей показателей преломления одномодовых оптических волокон, которые, помимо требуемой минимизации хроматической дисперсии, обеспечивают также необходимые механические характеристики, минимизацию рэлеевских потерь, технологичность производства и прокладки ОВ и т.д.
Сравнивая различные ОВ по их дисперсионным характеристикам, можно
отметить, что лучшими в этом плане являются одномодовые волокна и градиентные волокна с плавным законом изменения показателя преломления, хотя градиентные волокна имеют худшие характеристики по сравнению с одномодовыми.
1.8 Типичные характеристики волокон
Волокна в соответствии с их качеством могут быть расставлены в следующем порядке:
 Пластиковые PCS
 Стекло со ступенчатым индексом
 Волокно со сглаженным индексом
 Одномодовое волокно
 Чем меньше размер ядра, тем лучше качество.
26
 Стеклянное волокно лучше пластикового.
Отметим, что такого рода классификация ни в коей мере не исключает более детальной классификации и не претендует на исчерпывающее изложение
предмета. Волоконно-оптический кабель должен соответствовать конкретным
требованиям. При передаче только нескольких тысяч битов в секунду на несколько метров достаточно использовать пластиковый кабель. Пластиковое волокно дешевле, так же как и совместимые с ним компоненты: источники, детекторы и соединители. Использование одномодового волокна для таких задач походило бы на использование "Феррари" для поездки в соседний магазин. Выбор
волокон с заведомо худшими характеристиками определяется конкретной задачей. Каждое волокно хорошо по-своему.
Таблица 1.1 – Типичные характеристики волокон
Тип
волокна
Диаметр
Диаметр опядра
тической обо(мкм)1
лочки (мкм)
Одно-мо- 3.7
довое 5.0
9.3
6.1
Сглажен- 50
ный индекс 62.5
Ступенчатый
индекс
PCS
Пластик
NA
80 или 125
85 или 125
125
0.13
125
0.17
125
0.20
Максимальное затухание (дБ/км)
650
790
650
1300
1550
Максимальная полоса
пропускания (МГц/км)
10
2.3
2.4
0.4
0.5
0.6
125
0.275
3.0
0.7
85
125
0.26
2.8
0.7
100
140
0.29
3.5
1.5
200
300
380
440
0.27
0.27
6.0
6.0
200
485
735
980
350
500
750
1000
0.30
0.5
0.5
0.5
10
240
230
220
5000 при 850 нм
0.3 6 дисп./км2
0.25
0.5 600 при 850 нм
1500 при 1300 нм
0.3 200 при 850 нм
1000 при 1300 нм
0.4 200 при 850 нм
400 при 1300 нм
0.9 300 при 850 нм
500 при 1300 нм
6 при 850 нм
6 при 850 нм
20 при 790 нм
5 при 660 нм3
1.9 Кабели из оптических волокон
Волоконно-оптический кабель (ВОК) – кабельное изделие, содержащее
один или несколько оптических волокон, объединенных в единую конструкцию,
Диаметр моды приведен для одномодового волокна, реальный диаметр меньше.
Дисперсия на нанометр ширины источника.
3 Пластиковые волокна обычно используют на расстояния до 100 м, со скоростью передачи
50 Мбит/сек.
1
2
27
обеспечивающую их работоспособность в заданных условиях эксплуатации.
ВОК представляет собой сложную многокомпонентную систему, содержащую
не только оптические волокна – ключевой элемент ВОК, но и упрочняющие и
заполняющие элементы, разнообразные полимерные материалы, а в отдельных
случаях и металлические элементы.
ВОК применяется в оборудовании связи и устройствах с применением аналогичной техники в качестве направляющей системы передачи высокочастотных
электромагнитных излучений (света) и в особенности там, где требуется передавать огромное количество информации на большие расстояния.
Конструктивно ВОК состоит из скрученных по определенной системе оптических волокон, заключенных в общую защитную оболочку. Оптическое волокно 1 состоит из сердцевины и внешней оболочки с меньшим значением показателя преломления, выбранные для обеспечения полнового внутреннего отражения. На практике, как правило, оболочка волокна 2 покрыта слоем полимера
акрилата или полиимида. Эти покрытия защищают волокна от повреждений и не
влияют на оптические свойства волновода. При скручивании волокна группируются в пучки 3 или ленты и покрываются изолирующей оболочкой 4, полое пространство которых заливается герметизирующей смолой 5. Для снижения переходных влияний между волокнами используют специальные перегородки или
темные поглощающие волокна. При обеспечении требуемых механических и
эксплуатационных свойств В.-о.к. могут также содержать силовые (упрочняющие) элементы, например металлические тросы 6, изолированные в пластиковой
оболочке и демпфирующие оболочки 7. Если кабель прокладывается в грунте, то
вся конструкция покрывается броней 8. Для защиты оптических волокон от воздействий со стороны внешней среды (грунт, воздух, вода), кабельное изделие покрывают общей защитной оболочкой 9.
4
3
2
1
9
8
7
5
6
Рисунок 1.11 – Структура волоконно-оптического кабеля:
1 – оптическое волокно; 2 – покрывная оболочка; 3 – группа оптических волокон; 4 – изолирующая оболочка; 5 – герметизирующее заполнение (смола);
6 – силовой трос; 7 – демпфирующая оболочка; 8 – броня; 9 – общая защитная
оболочка
28
Для удобства подключения и отключения передающей и приемной аппаратуры связи в ВОК каждый конец оптического волокна оканчивается разъемным соединителем, который может быть изготовлен для одного или группы оптических волокон.
В зависимости от конструктивного исполнения ВОК делят на кабели внутренней и внешней прокладки, а также кабели для шнуров. По своему назначению
ВОК могут быть классифицированы на три группы: магистральные, зоновые и
городские. Магистральные ВОК предназначаются для передачи информации на
большие расстояния и значительное число каналов. Зоновые ВОК служат для организации многоканальной связи между областным центром и районами с дальностью связи до 250 км. Городские ВОК применяются в качестве соединительных линий между городскими АТС и узлами связи. Они рассчитаны на короткие
расстояния (до 10 км).
К настоящему моменту были предложены и испытаны многие типы кабелей.
Их можно разделить на три основные категории: 1) ленточная структура, 2) классическая структура, 3) цилиндрическая желобковая структура.
Разумеется, в конкретных случаях возможны комбинации разных структур.
Упомянем также о пучках волокон (жгутах), которые исторически были использованы первыми. Но вследствие их низких качеств при передаче оптических сигналов, а также низкой механической прочности теперь ими пользуются только для
освещения.
Волокно в защитной оболочке обладает механической прочностью, позволяющей применять обычные способы изготовления кабеля: волокна располагаются
вокруг центральной жилы при помощи специального сборочного механизма. Можно
разместить на одной центральной жиле один или несколько слоев волокон (рис.
1.12) или собрать кабель из нескольких многожильных элементов (рис. 1.13).
Рисунок 1.12 – «Классический» кабель Рисунок 1.13 – «Классический» каиз 6 оптических волокон
бель, образованный 6 «многожиль1 – полиэтиленовая оболочка; 2–алюми- ными» сборками из оптических волокон
ниевая трубка: 3 – медный несущий
стержень или стеклянное волокно с по- 1 – полиэтиленовая оболочка; 2 –
крытием; 4 – оптическое волокно с за- центральный металлический стерщитным покрытием.
29
жень; 3 – сборка из оптических волокон; 4 – оптическое волокно с защитным покрытием; 5 – алюминиевая трубка.
Наружная оболочка кабеля должна быть рассчитана на рабочие условия (проводка по трубе, прокладка в земле и т. п.), и ее материал следует выбирать, исходя
из предполагаемых внешних воздействий.
Основные преимущества кабелей такого типа: волокно хорошо защищено, повышенная механическая прочность на разрыв, на сжатие и т. д., хорошо известны технология изготовления и оборудование, довольно высокая температурная стабильность.
Из недостатков отметим следующие: громоздкость, поскольку упрочняется
каждое отдельное волокно; высокая стоимость производства ввиду малой длины
отрезков кабеля; необходимость предварительного удаления оболочки при индивидуальном соединении волокон.
Этот тип оптического кабеля, разработанный фирмой Bell Laboratories высокую, допускает весьма высокую плотность волокон в заданном поперечном сечении. Из волокон составляется матрица m×n.
Матрица подразделяется на строки-ленты, которые легко накладываются
друг на друга.
Лента состоит из уложенных параллельно n волокон, причем шаг между
волокнами равен нескольким сотням микрометров. Волокна располагаются
между двумя листами пластмассы, каждый из которых состоит из двух слоев:
Рисунок 1.14 – Ленточный кабель в разрезе
1 – слой полиэфирной пластмассы; 2 – граница двух слоев; 3 – полиэтиленовый слой; 4 – оптическое волокно.
слоя полиэтилена с низким модулем упругости, который при нагревании прилипает к волокнам, и слоя полиэфира с высоким модулем упругости, который обеспечивает жесткость всей сборки (рис.1.14).
Если наложить друг на друга т таких лент, то получим матрицу m×n , которую затем скручивают и вводят как спираль в крепкую оболочку, армированную кордом с высоким сопротивлением на разрыв, который воспринимает внешние нагрузки, сохраняя матрицу неизменной.
Преимущества подобной структуры таковы:
30
1) возможность повышенной плотности упаковки волокон (пример: описанный кабель содержит 12×12=144 волокна при общем диаметре 12 мм);
2) возможность одновременного присоединения всех m×n волокон;
3) меньшая стоимость, поскольку защита n волокон достигается одной
операцией.
Из недостатков следует отметить:
1) наличие риска ломки волокон при изготовлении;
2) плохое распределение нагрузки на волокна при разных воздействиях на
кабель: изменение затухания в волокне в этом случае будет сильно зависеть от
положения волокна в матрице;
3) влияние температуры на столь компактную и неоднородную структуру;
4) сложность одновременного соединения m×n волокон.
Иная разновидность ленточного кабеля (рис. 1.15), где лента образована
ячейками из алюминия, позволяет избавиться от этих недостатков.
В этом случае центральной часть кабеля является сердечник с желобами
(пазами) в виде винтовой спирали, в которых в ненатянутом состоянии располагаются волокна, предварительно покрытые защитной оболочкой.
Рисунок 1.15 – Разновидность ленточного кабеля.
1 – лента из полиана; 2 – канал; 3 –
оптическое волокно без второго защитного покрытия; 4 – алюминиевая трубка;
5 – полиэтиленовая оболочка.
Рисунок 1.16 – Кабель цилиндрической желобковой структуры в
разрезе.
1 – защитная лента; 2 – защитная оболочка; 3 – оптическое волокно без второго защитного покрытия; 4 – центральный несущий стержень; 5 – пластмассовый сердечник.
Желобковая цилиндрическая структура кабеля (рис. 1.16) сочетает преимущества двух описанных выше: меньшая громоздкость, ограниченное число
манипуляций с волокнами в процессе изготовления; возможность обеспечить одновременную защиту многим волокнам, что снижает стоимость. Преимуществом также является то обстоятельство, что волокно легко поддается фиксации
в структуре, а также относительная легкость соединения сразу всех волокон каж-
31
дого сердечника. Следует, однако, напомнить о необходимости производить операции с волокном без вторичного покрытия, о хрупкости волокон, ближайших к
внешней оболочке кабеля, о необходимости располагать специальными сборочными механизмами.
Основными контролируемыми характеристиками ВОК при прокладке являются целостность волокон, их коэффициент затухания, наличие дефектов волокна с указанием их месторасположения, частотная характеристика, апертура,
профиль коэффициента преломления по сечению волокна, геометрические размеры. В соответствии с этими параметрами определяется и перечень измерительной аппаратуры, необходимой для проведения их испытаний.
Современные ВОК могут содержать до тысячи волокон в одном кабеле, с
потенциальной пропускной способностью до одного терабайта в секунду. По некоторым оценкам это составляет не более 1% от тех возможностей оптического
волокна, которые задействованы существующим оборудованием.
32
2 ИСТОЧНИКИ ОПТИЧЕСКОГО ИЗЛУЧЕНИЯ И УСИЛИТЕЛИ СВЕТА
2.1 Основные элементы оптического квантового генератора и оптиче-
ского усилителя
Квантовую электронику можно определить как раздел электроники, в котором фундаментальную роль играют явления квантового характера. Настоящая
книга посвящена рассмотрению частного аспекта квантовой электроники, а
именно описанию физических принципов действия лазеров и их характеристик.
Прежде чем заняться детальным обсуждением предмета, целесообразно уделить
некоторое внимание элементарному рассмотрению идей, на которых основаны
лазеры.
В лазере используются три фундаментальных явления, происходящих при
взаимодействии электромагнитных волн с веществом, а именно процессы спонтанного и вынужденного излучения и процесс поглощения.
Спонтанное излучение (рис. 2.1,а)
Рассмотрим в некоторой среде два энергетических уровня 1 и 2 с
энергиями E 1 и Е 2 (E 1 < Е 2 ). В последующем рассмотрении это могут быть
любые два уровня из неограниченного набора уровней, свойственных данной среде. Однако удобно принять уровень 1 за основной. Предположим,
что атом (или молекула) вещества находится первоначально в состоянии,
соответствующем уровню 2. Поскольку Е 2 > Е 1 атом будет стремиться перейти на уровень 1. Следовательно, из атома должна выделиться соответствующая разность энергий Е 2 – Е 1 . Когда эта энергия высвобождается в
виде электромагнитной волны, процесс называют спонтанным излучением.
При этом частота ν излученной волны определяется формулой (полученной
Планком)
ν =(Е 2 -Е 1 )/h
(2.1)
где h – постоянная Планка. Таким образом, спонтанное излучение характеризуется испусканием фотона с энергией hv = Е 2 – Е 1 при переходе
атома с уровня 2 на уровень 1 (рис. 2.1, а). Заметим, что спонтанное излучение только один из двух возможных путей перехода атома из одного состояния в другое. Переход может происходить также и безызлучательным
путем. В этом случае избыток энергии Е 2 – Е 1 выделяется в какой-либо
иной форме (например, разность энергии может перейти в кинетическую
энергию окружающих молекул).
33
Вероятность спонтанного излучения можно определить следующим
образом. Предположим, что в момент времени t на уровне 2 находятся N 2
атомов (в единице объема). Скорость перехода (dN2 /dt) спонт этих атомов
вследствие спонтанного излучения на нижний уровень, очевидно, пропорциональна N 2 . Следовательно, можно написать
(dN 2 /dt) спонт = - AN 2
(2.2)
Множитель А представляет собой вероятность спонтанного излучения и называется коэффициентом Эйнштейна А (выражение для А впервые
было получено Энштейном из термодинамических соображений). Величину τ спонт = 1 / А называют спонтанным временем жизни. Численное значение величины А (и τ спонт ) зависит от конкретного перехода, участвующего в излучении.
а
б
в
Рисунок 2.1 – Схематическое представление трех процессов,
а – спонтанное излучение; б – вынужденное излучение; в – поглощение.
Вынужденное излучение (рис. 2.1,б)
Предположим снова, что атом первоначально находится на верхнем
уровне 2 и на вещество падает электромагнитная волна с частотой ν, определяемой выражением (2.1) (т. е. с частотой, равной частоте спонтанно испущенной волны). Поскольку частоты падающей волны и излучения, связанного с атомным переходом, равны друг другу, имеется конечная вероятность того, что падающая волна вызовет переход (2→1) атома с уровня
2 на уровень 1. При этом разность энергий Е 2 – E 1 , выделится в виде электромагнитной волны, которая добавится к падающей. Это и есть явление
вынужденного излучения. Между процессами спонтанного и вынужденного излучения имеется существенное отличие. В случае спонтанного излучения атом испускает электромагнитную волну, фаза которой не имеет опре-
34
деленной связи с фазой волны, излученной другим атомом. Более того, испущенная волна может иметь любое направление распространения. В случае же вынужденного излучения, поскольку процесс инициируется падающей волной, излучение любого атома добавляется к этой волне в той же фазе. Падающая волна
определяет также направление распространения испущенной волны.
Процесс вынужденного излучения можно описать с помощью уравнения
(dN 2 /dt) вын = -W21 N 2 ,
(2.3)
где (dN 2 /dt)вын – скорость перехода 2→1 за счет вынужденного излучения,
a W21 – вероятность вынужденного перехода. Как и коэффициент А, определяемый выражением (1.2), величина W2l имеет также размерность (время)-1. Однако
в отличие от А вероятность W21 зависит не только от конкретного перехода, но и
от интенсивности падающей электромагнитной волны. Для плоской волны
можно написать
W2, = σ21F
(2.4)
здесь F – плотность потока фотонов в падающей волне, а σ21 – величина,
имеющая размерность площади (она называется сечением вынужденного излучения) и зависящая от характеристик данного перехода.
Поглощение (рис. 2.1, в)
Предположим теперь, что атом первоначально находится на уровне 1. Если
это основной уровень, то атом будет оставаться на нем до тех пор, пока на него
не подействует какое-либо внешнее возмущение. Пусть на вещество падает электромагнитная волна с частотой ν, определяемой выражением (2.1). В таком случае существует конечная вероятность того, что атом перейдет на верхний уровень 2. Разность энергий (Е 2 – Е 1 ) необходимая для того, чтобы атом совершил
переход, берется из энергии падающей электромагнитной волны. В этом заключается процесс поглощения.
По аналогии с (2.3) вероятность поглощения W12 определяется уравнением
dNJdt = – W12 N 1 ,
(2.5)
где N 1– число атомов в единице объема, которые в данный момент времени
находятся на уровне 1. Кроме того, так же, как и в выражении (1.4), можно написать
Wl2 = σ21F
(2.6)
здесь σ21 – некоторая характерная площадь (сечение поглощения), которая
зависит только от конкретного перехода.
35
В предыдущих разделах были даны основные понятия процессов спонтанного и вынужденного излучений, а также поглощения. На языке фотонов эти
процессы можно описать следующим образом (рис. 2.1):
1) в процессе спонтанного излучения атом, испуская фотон, переходит с
уровня 2 на уровень 1;
2) в процессе вынужденного излучения падающий фотон вызывает переход 2→1, в результате чего мы получаем два фотона (падающий плюс испущенный);
3) в процессе поглощения падающий фотон поглощается, вызывая переход
1→2. Следует отметить, что σ12= σ21, как показал Эйнштейн еще в начале XX в.
Это означает, что вероятности вынужденного излучения и поглощения равны
друг другу. Поэтому в дальнейшем мы будем писать σ12= σ21= σ, понимая под σ
сечение данного перехода. Число атомов в единице объема, находящихся на данном энергетическом уровне, будем называть населенностью этого уровня.
2.2 Требования к источникам излучения
Источник оптического излучения преобразует электрическую энергию
возбуждения в энергию оптического излучения заданного спектрального состава
и пространственного распределения.
Основные требования:
1 Совместимость с оптической средой передачи, т. е. длина волны
излучения должна соответствовать окнам прозрачности ОВ.
2 Высокая мощность излучения и эффективный ввод излучения в волокно.
3 Узкая спектральная полоса излучения и высокое быстродействие при
модуляции.
4 Длительный срок службы (не менее 105 часов).
5 Устойчивость источника к перегрузкам и изменению параметров окружающей среды.
6 Высокая технологичность производства и миниатюрность исполнения.
Указанным требованиям удовлетворяют полупроводниковые источники
излучения.
2.3 Характеристики полупроводниковых материалов
При рассмотрении процесса излучения света источником либо его поглощения фотодиодом свет рассматривается с квантовой точки зрения. Частицы
света называются фотонами.
Ранее была отмечена связь энергии фотона Еф и параметров световой
волны: Еф= h*f , где h=6,626*10-34 Дж*с – постоянная Планка, f – частота волны.
Через связь длины световой волны и частоты энергия фотона:
36
f 
c

 Eф 
hc
 ,
(2.7)
где с=3*108 м/с – скорость света.
 - длина волны - пространственный интервал при прохождении, которого
электромагнитная волна меняет свою фазу на 2  .
Собственными полупроводниками или полупроводниками типа i (от английского intrinsic - собственный) называются чистые полупроводники, не содержащие примесей.
Собственные полупроводники имеют кристаллическую структуру, характеризующуюся периодическим расположением атомов в узлах пространственной кристаллической решетки. В такой решетке каждый атом взаимно связан с
четырьмя соседними атомами ковалентными связями (рисунок 2.2).
Рисунок 2.2 –Кристаллическая решетка полупроводника типа i
При температуре абсолютного нуля (T=0° K) все валентные электроны
находятся в ковалентных связях, следовательно, свободные носители заряда отсутствуют, и полупроводник подобен диэлектрику. При повышении температуры или при облучении полупроводника лучистой энергией валентный электрон может выйти из ковалентной связи и стать свободным носителем электрического заряда (рисунок 2.3). При этом ковалентная связь становится дефектной,
в ней образуется свободное (вакантное) место, которое может занять один из валентных электронов соседней связи, в результате чего вакантное место переместится к другой паре атомов. Перемещение вакантного места внутри кристаллической решетки можно рассматривать как перемещение некоторого фиктивного
(виртуального) положительного заряда, величина которого равна заряду электрона. Такой положительный заряд принято называть дыркой.
37
Рисунок 2.3 –Кристаллическая решетка полупроводника типа i
с валентными электронами
Процесс возникновения свободных электронов и дырок, обусловленный
разрывом ковалентных связей, называется тепловой генерацией носителей заряда.
Возникшие в результате генерации электроны и дырки, находясь в состоянии хаотического теплового движения, спустя некоторое время, среднее значение которого называется временем жизни носителей заряда, встречаются друг с
другом, в результате чего происходит восстановление ковалентных связей. Этот
процесс называется рекомбинацией носителей заряда.
Электронным полупроводником или полупроводником типа n (от латинского negative - отрицательный) называется полупроводник, в кристаллической
решетке которого (рисунок 2.4) помимо основных (четырехвалентных) атомов
содержатся примесные пятивалентные атомы, называемые донорами. В такой
кристаллической решетке четыре валентных электрона примесного атома заняты
в ковалентных связях, а пятый (“лишний”) электрон не может вступить в нормальную ковалентную связь и легко отделяется от примесного атома, становясь
свободным носителем заряда.
Электроны в этом случае являются основными носителями заряда, а дырки
- неосновными.
Рисунок 2.4 –Кристаллическая решетка полупроводника типа n
Дырочным полупроводником или полупроводником типа p (от латинского
positive - положительный) называется полупроводник, в кристаллической решетке которого (рисунок 2.5) содержатся примесные трехвалентные атомы,
называемые акцепторами. В такой кристаллической решетке одна из ковалентных связей остается незаполненной. Свободную связь примесного атома может
заполнить электрон, покинувший одну из соседних связей.
38
Рисунок 2.5 –Кристаллическая решетка полупроводника типа p
Согласно представлениям квантовой физики электроны в атоме могут принимать строго определенные значения энергии или, как говорят, занимать определенные энергетические уровни.
Твердое тело, каковым является полупроводниковый кристалл, состоит из
множества атомов, сильно взаимодействующих друг с другом, благодаря малым
межатомным расстояниям. Поэтому вместо совокупности разрешенных дискретных энергетических уровней, свойственных отдельному атому, твердое тело характеризуется совокупностью разрешенных энергетических зон, состоящих из
большого числа близко расположенных энергетических уровней.
Заполненная электронами разрешенная зона называется валентной зоной
(ВЗ), а следующая за ней незаполненная зона называется зоной проводимости
(ЗП). У полупроводников валентная зона и зона проводимости разделены запрещенной зоной (ЗЗ).
Зона проводимости
Ес – энергия ЗП
Запрещенная
зона
Еg - энергия ЗЗ
Еv – энергия ВЗ
Рисунок 2.6 – Энергетическая модель материала
Электрон, обладающий энергией валентной зоны, связан с атомами кристаллической решетки и пространственно локализован. Если же электрон занимает место в зоне проводимости, он свободен от валентной связи и имеет возможность перемещаться в молекулярной структуре материала. Изменение энергии электрона представляет собой квантовый переход.
Так как EC  EV , то для перехода электрона в ЗП необходимо сообщить дополнительную энергию, например, в виде кванта E g  EC  EV  EФ , при этом
наблюдается поглощение фотона с образованием носителей заряда.
При переходе электрона из ЗП в ВЗ могут наблюдаться явления спонтанного или стимулированного излучения фотонов при рекомбинации носителей заряда.
39
Спонтанное излучение возникает при переходе любого электрона с произвольного уровня в зоне проводимости на любой уровень валентной зоны. Возбужденное состояние является нестабильным и через короткий промежуток времени без какого-либо внешнего воздействия атом переходит в основное состояние, испуская фотон.
Под стимулированным излучением понимается излучение возбужденных
электронов под действием падающего на них света. В рамках квантовой теории
вынужденное излучение означает переход электрона из высшего энергетического состояния в низшее, но не произвольно, а под влиянием фотона. Возникающая при излучении световая волна не отличается от падающей на атом волны
частотой, фазой, поляризацией и направлением распространения.
Длина волны излучения зависит от ширины ЗЗ материала и определяется

hc
hc

( Ec  Ev ) Eg .
Рисунок 2.7 –Квантовые переходы
Исходя из используемых в ВОСП спектральных диапазонов волн  =
0,8…1,6 мкм определено, что им соответствуют энергии запрещенной зоны
E g  0,1...5 эВ , которыми обладают полупроводники
III, IV, V групп таблицы
Менделеева.
Полупроводниковые материалы разделяются на прямозонные и непрямозонные. В прямозонных материалах процессы переходов носителей с уровня на
уровень происходят без задержки и сопровождаются высокой квантовой эффективностью.
Наибольшее применение в технике оптической связи получили примесные
полупроводниковые материалы, в которых внутри ЗЗ могут создаваться дискретные энергетические уровни. Примесные полупроводники образуют разные виды
проводимости электрического тока – электронную и дырочную.
40
Рисунок 2.8 –Энергетические диаграммы полупроводниковых материалов
Базовыми материалами для изготовления источников являются следующие прямозонные материалы: арсенид галлия GaAs и фосфид индия InP, трех и
четырехкомпонентные соединения на их основе – GaAlAs (арсенид галлия и алюминия), GaInAsP (фосфид галлия индия и арсенида), InGaAs (арсенид индия и
галия). Материалы пригодны для массового изготовления источников и безопасны при работе с ними.
На рисунке 2.9 изображена классификация источников ВОСП.
ИСТОЧНИКИ ИЗЛУЧЕНИЯ ВОСП
Светоизлучающие диоды
(СИД)
Лазерные диоды (ЛД)
Поверхностный СИД
ЛД с резонатором
Фабри-Перо (ФП-лазер)
Торцевой СИД
ЛД с распределенной
обратной связью
(РОС-лазер)
Суперлюминесцентный
СИД
ЛД с распределенным
брэгговским отражением
(РБО-лазер)
ЛД с поверхностным
излучением и
вертикальным
резонатором
Рисунок 2.9 – Классификация источников излучения ВОСП
41
2.4 Светодиоды
Принцип действия светоизлучающих диодов (СИД) основан на явлении
электролюминесценции, то есть излучения света материалами под действием
электрического поля. Излучение фотонов обеспечивается инжекционной электролюминесценцией. При протекании тока через p-n переход в прямом направлении наблюдается излучательная рекомбинация инжектированных не основных
носителей. Наибольшее применение получили гетеропереходы.
Гетеропереход – переход, образованный между материалами со сходной
кристаллической структурой, но обладающими разной шириной запрещенной
зоны и показателями преломления.
СИД имеет трехслойную структуру: пассивные слои (1) и активный слой
(2). В n-области свободные электроны занимают разрешенные уровни в зоне проводимости, а в p-области дырки занимают соответствующие уровни в валентной
зоне (рисунок 2.9).
Структура СИД
Диаграмма прямо смещенного перехода
Рисунок 2.10 – Распределение показателей преломления
В плоскости контакта p-n перехода возникает разность потенциалов – потенциальный барьер, препятствующий диффузии электронов в р-область и дырок n-область. При приложении прямого смещения наблюдается односторонняя
инжекция электронов и дырок в активный слой. Высокая концентрация носителей в активном слое обеспечивается скачком потенциала Е на границе гетероперехода. В активном слое наблюдается рекомендация носителей с выделением
избыточной энергии в виде фотонов света. СИД функционирует на основе спонтанного излучения и формирует некогерентные волны с
42

hc
Еg 2 .
Соотношение показателей преломления активного и пассивного слоев
n2>n1 обеспечивает волноводный эффект и повышает КПД источника.
При разработке конструкций СИД необходимо уменьшать поглощение фотонов полупроводником и обеспечить эффективный ввод излучения в волокно.
Различают две структуры СИД: поверхностный СИД (рисунок 2.11) торцевой СИД (рисунок 2.12).
В поверхностном СИД – излучение выводится с поверхности активного
слоя в перпендикулярной ему плоскости. Оптическое волокно («пиглейл») присоединяется к поверхности источника через специальную выемку в полупроводниковой подложке, что обеспечивает эффективный ввод мощности спонтанного
излучения в световод.
Рисунок 2.11 – Конструкция поверхностного СИД
В торцевом СИД – излучение выводится с одного торца активного слоя в
параллельной к нему плоскости. Другой торец активного слоя выполняется в
виде зеркала. Излучающий торец согласуется с ОВ линзовой системой.
43
Рисунок 2.12 – Конструкция торцевого СИД
В суперлюминесцентных диодах (СЛД) последовательно действуют два
процесса генерации света: первичное излучение возникает в результате спонтанной рекомбинации электронно-дырочных пар и вторичное - вынужденное излучение – является основой механизма усиления спонтанного излучения в активной среде. Активная среда в СЛД обладает высоким оптическим коэффициентом
усиления, оптический резонатор в СЛД отсутствует и такой излучатель, в целом,
можно рассматривать как однопроходный усилитель света. По конструкции СЛД
соответствует торцевому СИД, но работает при более высоких токах инжекции
от 50 до 100 мА.
2.5 Резонаторы лазеров
Лазер – термин обозначает усиление света путем вынужденной (индуцированной, стимулированной) эмиссии излучения (light amplitication by stimulated
emission of radiation). Аббревиатурой английских слов называется устройство,
обладающее удивительными свойствами, позволяющими использовать его в различных областях науки и техники: медицине, связи, обработке материалов, в записи информации, ее обработке и т.д. Началом лазерного эры считают 1960 год
– год создания первого лазера (Л.) на рубине.
Однако, интересно отметить, что слово «лазер» известно с 6 века до нашей
эры – так называлось растение, обладающее не менее замечательными свойствами, за которые его считали божьим даром. Оно произрастало около города
Кирены (современная Ливия) и применялось для лечения простуды, различных
эпидемических заболеваний и как противоядие. Примерно во втором веке до
44
нашей эры это растение исчезло, а слово приобрело новое значение, определяющее современный предмет, о котором также можно сказать: «Лазер – один из
чудеснейших даров природы, имеющий множество применений» (Плиний Старший, «Естественная история», ХХII; 49; 1 в. н.э.).
Принцип работы Л. основан на соединении двух основных элементов: усилителя света (активной среды) и резонатора, обеспечивающего положительную
обратную связь и селекцию частоты генерации. Их сочетание образует оптический квантовый генератор, подобный многим известным в физике генераторам
(электрическим, механическим).
Зеркала резонатора Фабри-Перо
a)
z
б)
Рисунок 2.13 – Схема лазера и физические процессы спонтанного
и индуктивного излучения, проходящие в активной среде а), конструкция
лазера с резонатором Фабри-Перо б)
На рис. 2.13, а показана схема лазера с резонатором в виде плоскопараллельных зеркал (резонатор Фабри-Перо). В активной среде возбужденный атом
может вернуться в свое основное состояние случайным образом, при этом испускается фотон. Частота, фаза, направление распространения случайны и не зависят от переходов других атомов, так называемый спонтанный переход. Возбужденный атом также может вернуться в основное состояние под действием внешнего электромагнитного поля. Конструкция лазера с резонатором Фабри-Перо
приведена рис. 2.13, б. При этом энергия первичного поля удваивается, так как
частота, фаза, направление распространения вторичного электромагнитного
45
поля совпадает с первичным. На рис. 2.14 это иллюстрируется возникновением
двух фотонов. В этом случае говорят об индуцированном (вынужденном или
стимулированном) излучении, которое используется для оптического усиления.
Безизлучательный
переход
Энергия
E3
Переход в
возбуждённое
состояние
E2
E1
Спонтанный или индуцированный переход
Рисунок 2.14 – Энергетическая диаграмма
Активного вещества с тремя уровнями
На рис. 2.14 показана энергетическая диаграмма активного вещества, имеющего три энергетических уровня. Энергия возбуждения, подводимая к активному веществу лазера, переводит атомы с основного энергетического уровня с
энергией Е1 на третий энергетический уровень (Е3). Атомы очень быстро переходят спонтанно на второй уровень с энергией Е2. Разность энергии Е3 - Е2 идет
на нагрев кристаллической решетки активного вещества. Со второго уровня (Е2)
частицы спонтанно переходят на основной уровень. С излучением фотона с энергией hν= Е2-Е1, где ν – частота излучения.
При разности энергии Е2-Е1=1÷3[эВ] излучение будет происходить на оптической частоте. Если увеличивать энергию возбуждения, то число частиц на
уровне Е2 будет больше чем на основном. Это явление называется «инверсной
населенностью», и первоначальное спонтанное излучение стимулирует индуцированные переходы, т.е. среда становится усиливающей.
В результате генерируется относительно узкая спектральная полоса когерентного излучения. Наличие зеркал приводит к отражению этого излучения обратно в активную среду. Таким образом происходит усиление первичного излучения путем его многократного прохождения через активную среду. Часть энергии при этом выводится из резонатора Л. для использования. Частота генерации
определяется частотой стимулированного перехода и резонансной частотой резонатора лазера. Спектральный интервал возможных частот генерации расширяется вследствие теплового движения атомов вещества их столкновения, расщепления уровня Е2 в сильном электрическом поле, некачественности зеркал и т.д.
Используя разные материалы, резонаторы и разные квантовые переходы можно
изготавливать Л. для многих применений и различных типов: твердотельные Л.,
газовые Л., Л. на красителях, химические Л., полупроводниковые Л., Л. на центрах окраски, Л. на свободных электронах, Л. на нелинейных эффектах.
46
В системах оптической связи широко применяются полупроводниковые
Л., так как их массогабаритные и технические характеристики наиболее полно
соответствуют требованиям этих систем.
Работа полупроводникового лазера на кристалле из арсенида-галия (GaAs)
впервые наблюдалась в 1962 г. Это был гомолазер, изготовленный при помощи
диффузии акцепторной примеси в кристалле GaAs. Если к pn-переходу полупроводника приложить прямое напряжение (напряжение в прямом направлении), то
в р-область будет происходить инжекция электронов, а в n-область – инжекция
дырок. Эти инжектированные неосновные носители, встречаясь с основными носителями, будут рекомбинировать, излучая свет длиной волны, соответствующей энергетической ширине запрещенной зоны Еg. Так как в этом случае концентрация неосновных носителей уменьшается при удалении от pn-перехода по
экспоненциальному закону, то ширина области светового излучения достигает
порядка диффузионной длины, т. е. нескольких микрометров. Поскольку диффузионная длина электрона много больше диффузионной длины дырки, то световое
излучение возникает в основном в р-области. В этой конструкции инжектированные носители занимают область ограниченную диффузионной длиной, малую по сравнению с областью распространения светоизлучения в кристалле.
Вследствие чего эффективное взаимодействие со светом затрудняется. Пороговое значение плотности тока оказывается высоким (более 50 кА/см2), и из-за
выделения тепла на постоянном токе при комнатной температуре лазерная генерация не возникает. Такой лазер обычно работает только в импульсном режиме
с большой скважностью.
Практическая реализация непрерывного режима работы полупроводникового лазера при комнатной температуре впервые была достигнута в 1970 г. (Ж.
И. Алферов, И. Хаяси и М. Б. Паниш). Был изготовлен лазер на двойной гетероетруктуре из материалов с различной шириной запрещенной зоны, что позволило уменьшить пороговую плотность тока при комнатной температуре до 1,6
кА/см2. Снижение порогового тока в гетеролазерах достигается за счет удержания инжектированных носителей в узкой области, ограниченной потенциальными барьерами гетероструктуры, а также за счет канализирования оптического
излучения в этой же области под действием волнового эффекта, возникающего
из-за различия в показателях преломления материалов гетероструктуры.
На рис. 2.15 показана структура энергетических зон. Так как на поверхности гетероперехода возникает гетеробарьер с энергией E , равной разности
энергетической ширины запрещенных зон, то этот гетеропереход будет препятствовать проникновению инжектированных носителей в слой покрытия. Это явление называется эффектом удержания носителей.
Обычно коэффициент преломления полупроводников для света с энергией, меньшей энергетической ширины запрещенной зоны, монотонно уменьшается с увеличением длины волны. Поэтому, если рассматривать длины волн излучения лазера, коэффициент преломления в слое покрытия с большой шириной
запрещенной зоны оказывается меньше коэффициента преломления активного
47
слоя и на границах гетероперехода возникает разность n в коэффициенте преломления (рис. 2.15, б). Так как свет концентрируется в месте с более высоким
коэффициентом преломления, то, как видно из рис. 2.15, в, он будет заключен
внутри активного слоя. Это явление называется эффектом удержания света.
48
Рисунок 2.15 – Структура энергетических зон гетероперехода:
49
а – инжекция электронов и дырок в активный слой; б–распределение коэффициента преломления; в – распределение светового излучения;
Поскольку при использовании двойной гетероструктуры свет и носители
удерживаются в активном слое и эффективно взаимодействуют, то оказывается
возможным получение полупроводникового лазера с низким пороговым значением тока. Уменьшение порогового тока достигается также сужением ширины
активной области. Для этого используются различные технологические приемы,
которые исключают растекание тока в боковом направлении, и, таким образом,
ограничивают ширину активной области. Это, так называемые полосковые лазеры с двойной гетероструктурой (ДГС лазеры) излучающие одну поперечную
моду.
Дальнейшее улучшение свойств активной среды основано на использовании кванторазмерных структур (КРС). Активная область в этом случае состоит
из слоев, толщина которых сравнима с длиной волны де Бройля для электронов
или дырок ( Б  h / p , где h - постоянная Планка, p - импульс электрона). В 80-х
гг. разработаны утонченные методы эпитаксии, позволяющие получать высокосовершенные структуры с толщиной слоев менее 10 нм. В таких слоях возникают
ограничения для движения электронов и дырок в направлении, перпендикулярном к поверхности слоя, что сопровождается изменением квантомеханических а
также оптических и электрических свойств слоя: увеличивается ширина запрещенной зоны, уменьшается спектр излучения, порог генерации КРС значительно
слабее, чем в массивных образцах, увеличивается с ростом температуры, что позволяет улучшить характеристики полупроводниковых лазеров.
Полосковые лазеры с резонатором Фабри-Перо широко применяются в системах телекоммуникаций. Однако для таких лазеров характерен широкий
спектр излучения (до 4 нм), смещение средней длинны волны при прямой модуляции (динамическая нестабильность) Л.. Для улучшения спектральных характеристик (ширина спектра излучения, средняя длина волны излучения) и обеспечения их стабильности предложено использовать резонатор с решеткой Брэгга,
которая формируется технологически с малым шагом и обеспечивает селекцию
одной продольной моды.
На рис. 2.16, а представлен лазер с распределенным отражением (DBR-лазер), представляющий собой конструкцию, в которой к внешнему световоду с
малыми потерями, связанному с активной областью, присоединена решетка,
формирующая избирательность коэффициента усиления в зависимости от длины
волны. В конструкции, показанной на рис. 2.16, б, оказывается возможным осуществлять необходимую для генерации лазера оптическую обратную связь даже
при формировании решетки внутри активного слоя. Эта конструкция носит
название лазера с распределенной обратной связью (DFB-лазер). На рис. 2.16, в
представлена конструкция двухрезонаторного лазера, в которой соединены два
50
лазерных резонатора различной длины. В этих конструкциях добротность резонатора различна для разных мод и может быть повышена для нужной резонансной моды.
Рисунок 2.16 – Виды динамических одномодовых лазеров:
а – DBR-лазер с распределенным отражением; б– DFB-лазер с распределенной обратной связью; в – двухрезонаторный лазер
Из-за разности в значении добротности выбранной моды с соседними резонансными модами даже при резком изменении усиления при непосредственной модуляции поддерживается устойчивая одномодовая генерация.
51
Л. с распределенной обратной связью имеют узкий (<0,1 нм) спектр излучения, высокую мощность излучения, но имеют более высокую стоимость и угловую расходимость излучения (пространственную характеристику) которая к
тому же несимметрична. Поэтому были разработаны лазеры с вертикальным резонатором и поверхностным излучением (Vertical Cavity Surface Emitting Laser –
VCSEL) структура которого приведена на рис. 2.17. Особенностью лазера является излучение в направлении перпендикулярном плоскости pn-перехода. В этом
же направлении формируется и Брэгговский резонатор. VCSEL имеют симметричную и очень узкую (менее 5◦) пространственную характеристику, технологичны в изготовлении, недороги и, хотя излучают меньшую среднюю мощность,
широко применяются в оптических системах.
Рисунок 2.17 – Схема структуры VCSEL-лазера
2.6 Оптические усилители
52
Рассмотрим в какой-либо среде два произвольных энергетических уровня
1 и 2 с соответствующими населенностями N 1 и N 2 . Пусть в этой среде в направлении оси z распространяется плоская волна с интенсивностью, соответствующей плотности потока фотонов F. Тогда в соответствии с выражениями (1.3) –
(1.6) изменение плотности потока dF, обусловленное как процессами вынужденного излучения, так и процессами поглощения, в слое dz (заштрихованная область на рис. 2.18) определяется уравнением
dF = σF{N 2 -N l )dz.
(2.7)
Из уравнения (2.7) следует, что в случае N 2 > N 1 среда ведет себя как усиливающая (т. е. dF/dz > 0), а в случае N 2 < N 1 – как поглощающая. Известно, что
при термодинамическом равновесии населенности энергетических уровней описываются статистикой Больцмана. Так, если N 1 е и N 2 е – населенности двух уровней при термодинамическом равновесии, то мы имеем
Ne2/ N 1 е = exp[-(E 2-E 1 )/kT],
где k – постоянная Больцмана, а Т –абсолютная температура среды. Таким образом, мы видим, что в случае термодинамического равновесия N 2 < N 1 . В соответствии с (2.7) среда поглощает излучение на частоте υ, что обычно и происходит. Однако если удастся достигнуть неравновесного состояния, для которого N 2
> N 1 , то среда будет действовать как усилитель. В этом случае будем говорить,
что в среде существует инверсия населенностей, имея в виду, что разность населенностей ( N 2 – N 1 > 0) противоположна по знаку той, которая существует в
обычных условиях ( Ne2 – N 1 е < 0). Среду, в которой осуществлена инверсия населенностей, будем называть активной средой.
53
Рисунок 2.18 – Изменение плотности потока фотонов dF при прохождении плоской электромагнитной волны через слой вещества толщиной dz
Если частота перехода υ = ( Е 2 – E 1 ) / h попадает в СВЧ - диапазон, то соответствующий усилитель называется мазером. Слово мазер (англ. maser) образовано из начальных букв слов следующей фразы: microwave amplification by
stimulated emission of radiation –усиление микроволн вынужденным испусканием
излучения. Если же частота перехода υ соответствует оптическому диапазону, то
усилитель называется лазером.
Для того чтобы усилитель превратить в генератор, необходимо ввести подходящую положительную обратную связь. В СВЧ - диапазоне это достигается
тем, что активную среду помещают в объемный резонатор, имеющий резонанс
при частоте υ. В лазере обратную связь обычно получают размещением активной
среды между двумя зеркалами с высоким коэффициентом отражения). В этом
случае плоская электромагнитная волна, распространяющаяся в направлении,
перпендикулярном зеркалам, будет поочередно отражаться от них, усиливаясь
при каждом прохождении через активную среду. Если одно из двух зеркал сделано частично прозрачным, то на выходе системы можно выделить пучок полезного излучения. Однако как в мазерах, так и в лазерах генерация возможна лишь
при выполнении некоторого порогового условия. Например, в лазере генерация
начинается тогда, когда усиление активной среды компенсирует потери в нем
(скажем, потери, обусловленные частичным выходом излучения из резонатора
через зеркало). В соответствии с выражением (2.7) усиление излучения за один
проход в активной среде (т. е. отношение выходной и входной плотностей потока
фотонов) равно exp[2σ (N2 – N 1 ) l ] , где l – длина активной среды. Если потери в
резонаторе определяются только пропусканием зеркал, то порог генерации будет
достигнут при выполнении условия R 1 R 2 e x p [ 2 e ( N 2 – N 1 ) l ] =1, где R1 и R2 –
коэффициенты отражения зеркал по интенсивности. Это условие показывает, что
порог достигается тогда, когда инверсия населенностей приближается к некоторому критическому значению ( N 2 – N1)кр, называемому критической инверсией
и определяемому соотношением
(N2-N1)KP = -ln(RlR2)/2σ l.
(2.9)
Как только достигнута критическая инверсия, генерация разовьется из
спонтанного излучения. Действительно, фотоны, которые спонтанно испускаются вдоль оси резонатора, будут усиливаться. Этот механизм и лежит в основе
лазерного генератора, называемого обычно просто лазером. Однако теперь слово
лазер широко применяется к любому устройству, испускающему вынужденное
излучение – будь то в дальнем или ближнем ИК-, УФ- и даже в рентгеновском
диапазонах. В таких случаях мы будем говорить соответственно об инфракрасных, ультрафиолетовых и рентгеновских лазерах. Заметим также, что названия
твердотельный, жидкостный и газовый лазер определяются агрегатным состоянием активной среды.
54
Рассмотрим задачу о том, каким образом в данной среде можно получить
инверсию населенностей. На первый взгляд может показаться, что инверсию
можно было бы создать при взаимодействии среды с достаточно сильной электромагнитной волной частоты υ, определяемой выражением (2.1). Поскольку при термодинамическом равновесии уровень 1 заселен больше,
чем уровень 2, поглощение преобладает над вынужденным излучением, т.
е. под действием падающей волны происходит больше переходов 1→2, чем
переходов 2→1, и можно надеяться осуществить таким путем инверсию
населенностей. Однако нетрудно заметить, что такой механизм работать не
будет (по крайней мере в стационарных условиях). Когда наступят условия, при которых населенности уровней окажутся одинаковыми ( N 2 = N 1 ) ,
процессы вынужденного излучения и поглощения начнут компенсировать
друг друга и в соответствии с (2.7) среда станет прозрачной. В такой ситуации обычно говорят о двухуровневом насыщении.
Рисунок 2.19 – Трехуровневая (а) и четырехуровневая ( б ) схемы лазера
Таким образом, используя только два уровня, невозможно получить
инверсию населенностей. Естественно, возникает вопрос: можно ли это
осуществить с использованием более чем двух уровней из неограниченного набора состояний данной атомной системы? Мы увидим, что в этом
случае ответ будет утвердительным и можно будет соответственно говорить о трех- и четырехуровневых лазерах в зависимости от числа рабочих
уровней (рис. 2.19). В трехуровневом лазере (рис. 2.19, а) атомы какимлибо способом переводятся с основного уровня 1 на уровень 2. Если выбрана среда, в которой атом, оказавшийся в возбужденном состоянии на
уровне 3, быстро переходит на уровень 2, то в такой среде можно получить
инверсию населенностей между уровнями 2 и 1. В четырехуровневом лазере (рис. 2.19, б) атомы также переводятся с основного уровня (для удобства будем называть его нулевым) на уровень 2. Если после этого атомы
55
быстро переходят на уровень 2, то между уровнями 2 и 1 может быть получена инверсия населенностей. Когда в таком четырехуровневом лазере
возникает генерация, атомы в процессе вынужденного излучения переходят с уровня 2 на уровень 1. Поэтому для непрерывной работы четырехуровневого лазера необходимо, чтобы частицы, оказавшиеся на уров не 1,
очень быстро переходили на нулевой уровень.
Мы показали, каким образом можно использовать три или четыре
энергетических уровня какой-либо системы для получения инверсии населенностей. Будет ли система работать по трех- или четырехуровневой
схеме (и будет ли она работать вообще!), зависит от того, насколько выполняются рассмотренные выше условия. Может возникнуть вопрос: зачем
использовать четырехуровневую схему, если уже трехуровневая ока зывается весьма эффективной для получения инверсии населенностей? Однако
дело в том, что в четырехуровневом лазере инверсию получить гораздо
легче. Чтобы убедиться в этом, прежде всего заметим, что разности энергий между рабочими уровнями лазера (рис. 2.19) обычно много больше,
чем kT, и в соответствии со статистикой Больцмана почти все атомы при
термодинамическом равновесии находятся в основном состоянии. Если мы
теперь обозначим число атомов в единице объема среды как N t , то в случае
трехуровневой системы эти атомы первоначально будут находиться на
уровне 1. Переведем теперь атомы с уровня 1 на уровень 2. Тогда с этого
уровня атомы будут релаксировать с переходом на более низкий уровень
2. Если такая релаксация происходит достаточно быстро, то уровень 3 остается практически незаселенным. В этом случае, для того чтобы населенности уровней 1 и 2 сделать одинаковыми, на уровень 2 нужно перевести половину атомов N t , расположенных первоначально на основном уровне. Инверсию населенностей будет создавать любой атом, переведенный на верхний уровень сверх этой половины от общего числа атомов. Однако в четырехуровневом лазере, поскольку уровень 1 первоначально был также незаселенным, любой атом, оказавшийся в возбужденном состоянии, будет да вать вклад в инверсию населенностей. Эти простые рассуждения показывают, что по возможности следует искать активные среды, работающие по
четырехуровневой схеме. Для получения инверсии населенностей возможно, разумеется, использование и большего числа энергетических уровней.
Процесс, под действием которого атомы переводятся с уровня 1 на уровень 3 (в трехуровневой схеме лазера) или с уровня О на уровень 3 (в четырехуровневой схеме), называется накачкой. Имеется несколько способов, с помощью которых можно реализовать этот процесс на практике, например при помощи некоторых видов ламп, дающих достаточно интенсивную световую волну,
или посредством электрического разряда в активной среде. Более подробное обсуждение процессов накачки читатель найдет в гл. 2. Однако следует заметить,
что если верхний уровень накачки пуст, то скорость, с которой верхний лазерный
56
уровень 2 станет заселяться с помощью накачки (dN2/dt)p, в общем случае можно
записать в виде
(dN2/dt)p = W p N g .
(2.10)
Здесь Ng – населенность основного уровня (т. е. уровня 1 или 0 соответственно на рис. 2.19, а и б), a Wp – коэффициент, который называется скоростью
накачки. Для того чтобы достигнуть пороговых условий, скорость накачки
должна превысить некоторое пороговое или критическое значение.
2.7 Полупроводниковые лазеры
Основные характеристики полупроводниковых лазеров приведены на рис.
2.20, 2.21, 2.22. Ватт-амперная характеристика (зависимость мощности излучения от тока накачки) у всех лазеров имеет характерный излом (рис.2.20) при пороговом значении тока накачки, вызванный тем, что лазерная генерация начинается при этом значении тока. Необходимо отметить, что пороговый ток накачки
увеличивается с ростом температуры. Это явление, обусловленное температурной зависимостью коэффициента усиления активной среды.
Рисунок 2.20 – ВтАХ полупроводникового лазера при изменении температуры
57
а)
1000
б)
2000
Рисунок 2.21 – Переходная (а) характеристика и характеристика
прямой модуляции полупроводникового лазера
58
Рисунок 2.22 – Диаграмма направленности излучения полупроводникового
лазера:
а - ширина диаграммы направленности, измеряется по уровню половинной мощности:
б- зависимость излучаемой мощности от угла во взаимно перпендикулярных направлениях
Ох и Оу
Самый простой метод модуляции излучения П.л состоит в изменении тока
инжекции I (прямая модуляция интенсивности излучения), при этом скорость
модуляции в импульсном режиме может достигать 10 Гбит/с и определяется временем нарастания фронта на переходной характеристики (Рис. 2.21, а), а полоса
модулирующих частот в аналоговых сигналах до 2 ГГц (определяется характеристикой прямой модуляции). (Рис. 2.21, б).
Поскольку электрческие и оптические явления в П.л. взаимосвязаны, при
высоких частотах модуляции наблюдается резонанс между инжектируемыми носителями заряда и электрическим полем, т.е. появляются затухающие колебания
интенсивности излучения около их стационарных значении (рис. 2.21,б).
Пространственные характеристики излучения П.л. (Рис. 2.22) определяются поперечным распределением поля в резонаторе и размерами излучающей
59
площадки. Диаграмма направленности излучения П.л. вследствие того, что у
большинства конструкций толщина активного слоя dx в несколько раз меньше
его ширины dy (dx <0,2мкм, dy <5 мкм), несимметрична: в плоскости, перпендикулярной р-n-переходу, 30 0 ...60 0 , в плоскости, параллельной ему - 5 0 ...10 0 (рис.
2.22.б).
Порог генерации и КПД полупроводникового лазера
Выведем формулы для порога генерации и КПД полупроводникового лазера. Так как активный слой представляет собой диэлектрический световод,
Рисунок 2.23 – Резонатор полупроводникового лазера
то толщина активного слоя d, при которой имеет место распространение
только одной поперечно» моды, должна удовлетворять условию
d
60

2 2  n1
,
(2.11)
где Δ – относительная разность коэффициентов преломления Δ=(n12–
Значение d, при которой имеет место только одна поперечная мода, в
случае λ= 1,55 мкм, n1= 3,54, Δ=0,1 оказывается менее 0,5 мкм.
Условие возникновения генерации оптического лазера является условием
равенства оптического усиления потерям энергии, при однократном прохождении света туда и обратно между двумя отражающими гранями резонатора (рис.
2.6) и представляется в виде
n22)/(2n12).
1
1
g th      ln
,
l
R1R2
(2.12)
где gth – коэффициент усиления активного слоя, необходимый для лазерной генерации,  – коэффициент удержания света, представляющий собой отношение энергии, заключенной внутри активного слоя, к оптическому выходу
g 
поперечной моды. Произведение th
называется коэффициентом усиления
моды. l – длина резонатора, R1 и R2 – коэффициенты отражения or граней резонатора, а – потери на поглощение внутри резонатора. (1 / l ) ln R1R2 называются
потерями на отражение и соответствуют величине оптического выхода лазера во
внешнее пространство. Используя коэффициент поглощения  ас активного слоя
и коэффициент поглощения  ех слоя покрытия, получаем следующее значение
для потерь моды:
   ас     ех (1   ).
(2.13)
Коэффициент усиления g возрастает пропорционально концентрации носителей N в активном слое и, если коэффициент пропорциональности обозначить через А0, имеет вид
g  A0 ( N  N g )  A0 N  in ,
(2.14)
где Ng – концентрация носителей, при которой гасится поглощение между
зонами и возникает усиление. В данном случае она входит в состав  in .
Если время жизни носителей обозначить через  s , то концентрация носителей N в активном слое будет выражаться следующей формулой:
N
s
ed
J,
(2.15)
61
где Ј – плотность тока инжекции, а е – заряд электрона.
В соответствии с изложенным ранее  s обратно пропорционально N, а
именно  s = (BeffN)-1. Принимая это во внимание, на основании формул (2.14) и
(2.15) получаем следующее выражение:
g
A0
eBeff
J
  in ,
d
(2.16)
представляющее собой зависимость между коэффициентом усиления и
плотностью тока инжекции. Beff называется эффективным коэффициентом рекомбинации.
Так как плотность тока при g=gth становится равной пороговой плотности
тока Јth, то на основании формул (2.12) и (2.16) для пороговой плотности тока
получаем следующее выражение:
2
eBeff d 
1
1 
J th 




_
ln
 .
2
2  in
l
R1R2 
A0  
(2.17)
Пороговая плотность тока Јth, как видно из формулы (2.17), падает с уменьшением толщины d активного слоя. Это объясняется тем, что, как видно из формулы (2.16), коэффициент усиления связан с объемной плотностью J/d тока. Однако, как показывает пример расчета, показанный на рис. 2.24, при толщине активного слоя d менее 0,1 мкм имеет место резкое возрастание пороговой плотности тока Јth. Причина этого заключается в том, что с уменьшением толщины активного слоя уменьшается эффект удержания света, распределение энергии поперечной моды распространяется на слой покрытия, коэффициент усиления поперечной моды падает. Это уменьшение коэффициента удержания света становится особенно заметным при толщине активного слоя d менее 0,1 мкм.
62
Рисунок 2.24 – Зависимость пороговой плотности тока Јth, от толщины активного слоя d GaInAsP/InP-лазера (λ=1,3 мкм) при комнатной температуре
(контакт по всей поверхности)
Минимальная пороговая плотность тока Јth имеет место при значениях d =
0,l – 0,15 мкм, поэтому толщину активного слоя полупроводникового лазера
обычно выбирают в этих пределах. Поскольку Јth меняется в зависимости от d,
то для оценки возможностей лазера во многих случаях используют отношение Јth
/d. Если это значение порядка 2...5 кА/см2/мкм, то лазер считается хорошего качества.
Другим важным параметром, характеризующим качество полупроводникового лазера, является дифференциальный квантовый выход. Дифференциальный квантовый выход ηd задается крутизной линейной части ватт амперной характеристики (L – I) и определяется формулой
d 
L / 
,
I / e
(2.18)
где ΔI/е – число носителей, инжектированных в единицу времени в активную область, a ΔL/ħω – число фотонов, излучаемых лазерным резонатором в единицу времени.
Если ηd выразить через параметры резонатора, то получаем
63
1
1
ln
l
R1R2
 stim(1  R1 )
d 

,
(1  R1/ R2 )(1  R1/ R2 )   1 ln 1
l
R1R2
(2.19)
Здесь оптический выход рассматривается со стороны R1. Обычно ηstim=l.
Из формулы (2.19) видно, что Если ηd с уменьшением R1 возрастает. Поскольку энергия излучается с обоих торцов резонатора, то при R1=R2 может быть
использована половина оптического выхода, другими словами, максимальное
значение ηd составляет 50%. В реальных лазерах это значение лежит в пределах
30–45%. Однако если поддерживать постоянным произведение R1R2 и увеличивать коэффициент отражения с одной стороны, делая конструкцию асимметричной, то при неизменном пороговом значении оказывается возможным повысить
ηd. Это ясно видно из формул (2.17) и (2.19). В последнее время начата разработка лазеров такой конструкции.
Полупроводниковый лазер представляет собой «пороговый прибор», поэтому даже при неизменном токе смещения изменение температуры окружающей среды может привести к изменению порогового значения, а вместе с тем к
изменению оптического выхода лазера. Эти изменения особенно заметны в приборах с высоким дифференциальным квантовым выходом. Следовательно, при
использовании этих приборов в системах оптической связи, к ним необходимо
добавить схему автоматической регулировки мощности, которая обеспечивала
бы постоянство оптического выхода. Оптический выход с одной стороны используется в качестве монитора. Температурная зависимость порогового значения приближенно выражается следующей формулой:
T 
I  I 0 exp ,
 T0 
(2.20)
где Т0 – характеристическая температура, которая у AlGaAs/ /GaAs-лазера
лежит в пределах 130–180 К, а у GalnAsP/InP-лазера – при комнатной температуре лежит в пределах 50– 70 К.
64
65
Рисунок 2.25 – Спектр генерации лазера с управляемым коэффициентом
преломления
В спектре лазера с управляемым коэффициентом преломления в окрестности порогового тока, как видно на рис. 2.25 появляются многочисленные продольные моды, однако при оптическом выходе свыше 1–2 мВт возрастает интенсивность только одной продольной моды и возникает генерация только одной
продольной моды, т. е. происходит сужение спектра.
Если увеличивать ток инжекции, то, как видно из спектра, приведенного
на рис. 2.25, мода генерации совершает последовательный перескок на продольную моду с большей длиной волны. Это обусловлено тем, что при повышении
температуры активного слоя кривая усиления сдвигается в сторону более длинных волн. На рис. 2.26 показана температурная характеристика длин волн излучения лазера. Длина волны излучения при изменении температуры окружающей
среды периодически перескакивает на несколько десятых долей нанометра в
направлении более длинных волн. Усредненное изменение длины
Рисунок 2.26 – Температурная зависимость длины волны λ, излучения лазера
волны для AlGaAs-лазеров составляет 0,3 нм/°С, а для GaInAsP-лазеров – 0,4-0,5
нм/°С. Даже в области отсутствия перескока моды длина волны излучения лазера
66
понемногу смещается в сторону более длинных волн. Это зависит от температурного коэффициента показателя преломления и составляет приблизительно 0,1
нм/°С. Длина волны продольной моды определяется условием резонанса лазерного резонатора, которое представляется в виде
  l  m ( m  целое число),
(2.21)
где β – постоянная распространения, равная (2π/λ)-neq,
neq – эквивалентный коэффициент преломления.
Таким образом, величина скачка продольной моды составляет
 
2
2neff l
,
(2.22)
где neff – эффективный коэффициент преломления, который, если принять
во внимание дисперсию показателя преломления в зависимости от длины волны,
будет представляться следующим выражением: (neq – λ·dneq/dλ). Можно считать,
что для AlGaAs-лазера neff = 4,2, а для GaInAsP-лазера neff = 2.8.
При осуществлении импульсной модуляции путем инжекции импульса
тока в полупроводниковом лазере на форму выходного сигнала лазера, как показано на рис. 2.21, а, накладываются затухающие колебания с частотой порядка
нескольких ГГц. Это связано с возникновением фазового запаздывания при взаимодействии света и носителей. Такие релаксационные колебания очень сильно
ограничивают область модуляции полупроводникового лазера и представляют
на практике большую проблему. Следует отметить, что эта проблема существовала только на начальном этапе разработки полупроводниковых лазеров. Благодаря использованию узкополосковых лазеров удалось подавить эти релаксационные колебания, так что в настоящее время почти нет никаких проблем, связанных с ними. В данном разделе кратко рассматриваются основные моменты, связанные с непосредственной модуляцией.
Частотный отклик промодулированного света полупроводникового лазера
при слабом сигнале имеет вид
S m ( )

S m (0)
1
2
  
   1

  i

1  
  ГО р 
  ГО 
  ГО   ГО s

,
(2.23)
67
Рисунок 2.27 – Пример расчета частотной зависимости модуляционной

чувствительности (Sm(ω)/Sm(0)) ( р =1 пс,т8=3 нс,  s =2-108 см-3, ξ = 0,5, A0 =5-1017 см2)
где
 1  I b

  1,
 ГО 2  (1   p N g A0 c)


  s p  I th 
(2.24)
т. е. имеет такой же вид, как у LCR-резонансного контура электрической
цепи, где τs и τр – соответственно время жизни носителей и фотонов, с – скорость
света.
На рис. 2.27 приведены примеры расчета частотной характеристики модуляционной чувствительности |Sm(ω)/Sm(0) |. Явление резонанса наблюдается, когда модуляционная чувствительность принимает максимальное значение
на
68
частоте fr, fr называется резонансной частотой. При f>fr модуляционная чувствительность резко падает. Это значение fr становится критерием верхней частоты
непосредственной модуляции полупроводникового лазера. Fp называют резонансным пиком. Частота релаксационных колебаний, показанная на рис. 2.28, а,
почти совпадает с частотой fr. Это связано с тем, что релаксационные колебания
возникают под влиянием лазерного резонанса. Высокая модуляционная чувствительность относительно составляющей частоты fr, заключенной в импульсном
токе, приводит к выделению составляющей fr в промодулированном свете. Следовательно, если окажется возможным уменьшить Fp, то тем самым будут подавляться релаксационные колебания. Так как обычно ωr0τp<<1, ωr0τs>>1, то из формулы (2.23) получаем следующее приближенное выражение:
 1  1
f r  1   p N g A0 c  
 2   s p
Ib
 1.
I th
(2.25)
Рисунок 2.28 – Зависимость резонансной частоты fr от тока смещения
Для удобства первое подкоренное выражение в вышеприведенной формуле полагают равным единице, хотя в полупроводниковых лазерах обычно не
выполняется условие ξτpNgA0c<<1. Поэтому будем использовать вышеприведенную формулу (2.16) в неизменном виде.
На рис. 2.22 приведен пример расчета резонансной частоты. Поскольку
значение  ы з составляет порядка 0,05 нc, т. е. невелико, то частота
нескольким гигагерцам и возрастает с увеличением тока смещения.
равна
69
Шумы в полупроводниковых лазерах
В полупроводниковых лазерах различают следующие шумы: 1) квантовый
шум, 2) шум токораспределения, 3) шум, обусловленный перескоком моды, 4)
шум, обусловленный отраженным светом. Квантовый шум обусловлен статистическими колебаниями в процессе случайного спонтанного излучения, имеет пик
при пороговом значении тока и периодически принимает максимальные значения на резонансных частотах. В лазерах, генерирующих большое число продольных мод, как и в лазерах с управляемым усилением, возникает модуляция интенсивности света, основанная на конкуренции одной моды с отдельными генерирующими модами. Эти шумы называются шумами токораспределения. Шумы,
обусловленные перескоком моды, возникают в моменты, когда продольная мода
перескакивает на следующую моду, что обусловливает обмен энергией между
двумя модами при перескоке. На рис. 2.19 показана характеристика интенсивности шума при неизменном смещении и изменении температуры в полупроводниковом лазере. Относительная интенсивность шума определяется следующим образом:
RIN 
где
(P) 2 1
 ,
P2 B
(2.26)
RIN – относительная интенсивность шума,
Р – средний оптический выход,
ΔР – флуктуации оптического выхода,
В – измеренная ширина полосы.
Нижняя граница шума, приведенного на рис. 2.18, представляет собой
квантовый шум, а пикообразные всплески – шум, обусловленный перескоком генерирующей моды при изменении температуры.
Если с повышением когерентности излучения полупроводникового лазера,
как показано на рис. 2.29, свет, отраженный от внешней точки, возвращается
внутрь лазера, то возникает сильный шум, обусловленный флуктуацией фазы.
Он называется шумом, вызванным отраженным светом. Доля света, вернувшегося после отражения от торца, по отношению к оптическому выходу лазера (коэффициент оптической обратной связи) оказывается высокой, лежащей в пределах 0,01–1%. Возникает сильный шум, достигающий RIN = 10-11. При значении
выше 1% уровень этого шума становится на порядок выше квантового шума,
стабилизируется и никаких шумовых пиков не возникает.
70
Рисунок 2.29 – Шум, обусловленный перескоком моды в полупроводниковом лазере (при отсутствии отраженного света)
Это связано с тем, что при увеличении отраженного света возникает многомодовая генерация и когерентность ухудшается. На практике подавление
шума, обусловленного отраженным светом, осуществляют путем 1) использования развязывающего устройства, 2) использования лазеров с управляемым усилением и осуществления высокоскоростной модуляции.
2.8 Соединение источников с волокном
С учетом различия апертур источника излучения и световода разработан
ряд элементов ввода – вывода излучения. Они выполняют функцию оптического
согласования угловых апертур активных элементов (светодиодов и лазеров) и
световодов. Показатели преломления полупроводниковых материалов, из которых изготавливаются СИД и ППЛ, имеют размерность около 3,5 (ППЛ  3,5), а
стекловолокно – около 1,5. Еще больше проблем с выводом/вводом излучения
через воздушный зазор, так как показатель преломления воздуха мало отличается от единицы (nв = 1,001). Условие полного внутреннего отражения при распространении света на границе раздела сред полупроводник–воздух имеет вид:
71
,
(2.27)
 КР = критический угол вывода (рисунок 2.30)
Рисунок 2.30 – Вывод излучения из световода
При этом доля излучаемой мощности составит:
(2.28)
Вместе с тем лучи, достигшие поверхности раздела сред в пределах КР
испытывают некоторое отражение на неоднородностях поверхностей (полупроводника и стекловолокна). Коэффициент, учитывающий это рассеяние, вычисляется:
(2.29)
Эффективность вывода излучения
(2.30)
где Р0 – излученная мощность в активном слое.
72
Эффективность составит
(2.31)
Для повышения эффективности ввода излучения в стекловолокно используются различные линзы, позволяющие сконцентрировать световой луч, что эквивалентно увеличению апертуры.
На рисунках 2.31 – 2.34 представлены различные линзовые соединители,
которые согласуют световоды и излучатели.
Рисунок 2.31 – Согласование микролинзой
Рисунок 2.32 – Согласование линзой на световоде
Рисунок 2.33 – Согласование линзой на излучателе
73
Рисунок 2.34 – Согласование градановой линзой
74
3 КОМПОНЕНТЫ МОДУЛЯЦИИ ОПТИЧЕСКОГО ИЗЛУЧЕНИЯ
Для передачи информации по оптическому волокну необходимо изменение параметров оптической несущей в зависимости от изменений исходного сигнала. Этот процесс называется модуляцией.
Модуляция излучения – это изменение параметров оптической несущей по
закону информационного колебания.
В ВОСП используют прямую (непосредственную) и внешнюю модуляцию
электромагнитных излучений оптического диапазона.
3.1 Модуляция оптического излучения
Наиболее простым с точки зрения реализации видом модуляции является
прямая модуляция оптической несущей по интенсивности на основе полупроводникового источника излучения. Интенсивность излучения – средняя мощность, переносимая волной за одну секунду через волновую поверхность площадью один квадратный метр.
Выходное излучение полупроводникового светодиода или лазера можно
непосредственно модулировать изменением характеристик активного слоя (тока
накачки/инжекции, объема резонатора лазера) так, чтобы получить модуляцию
мощности излучения. Чаще всего при прямой модуляции изменяется выходная
мощность за счет изменения величины силы тока накачки/инжекции, в зависимости от изменений информационного сигнала.
Резонатор
t
Активная среда
Модулятор
t
Накачка
Рисунок 3.1 – Принцип прямой модуляции
Если в качестве модулирующего сигнала используется электрический цифровой сигнал, то на выходе источника формируется оптический сигнал с двумя
дискретными значениями мощности Pmax и Pmin.
Pmax – соответствует "1" информационного сигнала.
Pmin – соответствует "0" информационного сигнала.
При модуляции интенсивности выбирается линейный участок ватт-амперной характеристики излучателя.
Сигнал на выходе источника определяется выражением:
75
Ps  Po(1  M * S (t )),
(3.1)
где Ро – постоянная мощность излучения, соответствующая току смещения
m – параметр глубины модуляции
m
P max  P min
P max
(3.2)
S(t) - модулирующий сигнал.
Pизл
Pизл
Pmax
Pmin
Iсм
t
Iн
Рисунок 3.2 – Модуляция цифровым сигналом мощности источника излучения
Достижимой является величина параметра глубины модуляции m до 0,9
(90%), однако при этом начинают проявляться нелинейные искажения. Нелинейные искажения приводят при модуляции к искажению формы сигнала и изменению его спектра. В спектре кроме частоты основного сигнала ω, появляется
также вторая и третья гармоники с частотами 2ω и 3ω. В спектре после демодуляции кроме 2ω и 3ω, появляется комбинационные продукты, которые полностью перекрывают полезный сигнал, и если амплитуда такой помехи будет соизмерима с амплитудой сигнала, то выделить такой сигнал крайне сложно. Поэтому на искажения введены показатели для оценки нелинейности: затухание нелинейности по второй и третьей гармоникам
a H 2  10 * lg
P1
 55дБ
P2
a H 3  10 * lg
P1
 60дБ
P3
Математическое описание работы модулятора
76
(3.3)
Pи 
Е
 е где – τе- время жизни элекМощность излучения определяется
трона, Е  Е М  COS t    - оптическая несущая представлена вектором
напряженности.
Чем меньше τе, тем больше Е.
РИ   е
Е
NФ 
ЕФ

ЕФ
отсюда:
  Nе  h  f
N  ЕФ
I
h f
I S
РИ  Ф
 кв
 кв  Н 
 Н
е
t
q
е
е
где S – крутизна ВтАХ.
Приложим в точку IН0 сигнал i  I m  COS   t 
PИ 
IН  S
е

S
е
 I Н 0  i  
S
е
 IН0 
РИ
S
е
 I m  COS   t   P0  Pm  COS   t 
а/
а
IН
Рисунок 3.3 - Ватт-амперная характеристка ЛД
Модулирующий однополярный сигнал подается в точку «а», для получения максимальной амплитуды на выходе источника излучения.
Участок аа/ является квазилинейным, он характеризуется слабо
выраженной нелинейностью. Данный участок аа/ описывается степенным рядом:
Р  a1  i 1  a 2  i 2  a3  i 3  ... 
(3.4)
где а1,а2,а3 – характеризуют нелинейность участка аа , i – информационный
сигнал, который подается в рабочую точку ВтАХ.
/
i  I m  COS   t   a1  I m  COS   t   a2  I m  COS 2   t   a3  I m  COS 3   t  
2
 a1  I m  COS   t  
COS 2t 
COS 3t 
3
a
a2
2
3
 I m  SIN 2  t   3  I m  SIN 3  t *
2
4
1
1  SIN 2  t 
2
1
3SIN   t   SIN 3  t 
4
77
Из выражения (*) видно, что в спектре кроме частоты основного сигнала
ω, появляется также 2 и 3 гармоники с частотами 2ω и 3ω.
Определим из соотношения (*) амплитуды 1-ой,2-ой, 3-ой гармоник:
Im
Iн  S
m
; Pи 
I0
е
аН2, аН3 показывают на сколько уровень полезного сигнала больше, чем уровень
2-ой и 3-ей гармонических составляющих.
Р1Г  а1 
Im
2
 a1 
I0  m
2

a1  P0   e  m
2S
Р2 Г
- амплитуда первой гармоники;
а2  I m 
а2
а2 P0   2 e  m 2
2
2
 
   I0  m  
2  2
4
4
S2
- амплитуда второй гармо2
2
ники;
а3  I m 
а3
а3 P0   3 e  m 3
3
3
 
 I0  m 

 
4  2 8 2
S3
8 2
- амплитуда третьей
3
Р3 Г
3
гармоники.
Прямая модуляция применима не только к СД и полупроводниковым лазерам. В принципе её можно использовать и для других типов лазеров. Если для
модуляции полупроводникового лазера управляют инжекционным током, то у
лазеров с оптической накачкой изменяют излучение накачки, а при других способах возбуждения лазеров управляют соответствующим возбудителем. Можно
регулировать также добротность или резонансную частоту оптического резонатора, что приводит к модуляции выходного излучения по интенсивности либо
частоте. Для безынерционной модуляции без искажений с малой глубиной по
лупроводникового лазера частота модуляции должна быть
1
 p
I
1
In
, где
I n - пороговый ток. В полупроводниковых лазерах электроны имеют короткое
рекомбинационное время жизни   10 9 c , а потери в оптическом резонаторе
настолько велики, что фотоны затухают еще быстрее с  p  10 c . При этих значениях времени жизни возможна прямая модуляция полупроводникового лазера
с достаточно высокой частотой.
Для твердотельных лазеров с оптической накачкой и газовых лазеров ве12
8
личины  и  p намного больше, а именно у Nd-YAG-лазера   10 3 c и  p  10 c
, а у He-Ne-лазера   10 7 c и  p  10 c . Такие большие времена жизни ограничивают прямую модуляцию этих лазеров столь низкими частотами, что она теряет
9
78
практическое значение. Медленно протекают и переходные процессы при включении и выключении твердотельных лазеров.
Обычно излучение твердотельных лазеров с оптической накачкой и газовых лазеров модулируется внешними модуляторами, отделенными от лазеров.
В этих модуляторах используются материалы, у которых либо показатель преломления, либо поглощение световой волны изменяется модулирующим сигналом. Управление показателем преломления основывается либо на электрооптическом эффекте (на величину п влияет электрическое поле), либо на магнитооптическом эффекте (на величину п действует магнитное поле), либо на пьезооптических эффектах (на величину п влияют пьезоэлектрические изменения плотности). В модуляторах для оптической связи используется преимущественно
электрооптический эффект. Материалы с выраженным магнитооптическим эффектом непрозрачны для света. Пьезооптические модуляторы получаются сложнее, чем электрооптические, и более громоздки.
Поглощение материала на световых волнах изменяется благодаря эффекту Франца — Келдыша. Речь идет о смещении границы поглощения полупроводника в электрическом поле, благодаря чему на частотах, примыкающих к
этой границе, поглощение меняется очень сильно. Итак, наиболее подходящим
для внешней модуляции света является электрооптический эффект и эффект
Франца-Келдыша, на которых работает электроабсорбционные модуляторы. Поэтому данные эффекты и основные на них модуляторы будут рассмотрены подробно.
Амплитуда 1,2,3 гармоник зависит от коэффициента модуляции m, крутизны ВтАХ – S, времени жизни электрона τе и среднего значения мощности –
Р0. Для того чтобы получить номинальные значения затухания нелинейности,
необходимо уменьшить коэффициент m, выбирать материалы с малым τе, работать при малом значении мощности. Но последнее условие противоречит получению максимального значения амплитуды выходного сигнала. Поэтому управлять необходимо либо m, либо τе.
Для достижения указанных ранее значений ан2 и ан3 могут применяться различные методы уменьшения нелинейных искажений: предискажение, использование отрицательной обратной связи, фазовая компенсация и другие. На рисунке
3.4 показана схема применения ООС.
79
Ус
βоос
Si(t)
ФД
ОВ
Uпит
Ус
R
Рисунок 3.4 – Схема оптического модулятора с ООС
Для того чтобы увеличить затухание нелинейности в схеме модулятора создается петля ООС. То есть часть излучения снимается и подается на ФД. Далее
сигнал уже в электрическом виде усиливается и подается на вход оптического
модулятора. Применение ООС позволяет увеличить затухание нелинейности на
величину 10-15 дБ.
Основные характеристики прямой модуляции
Частотная характеристика модуляции с СИД.
Для модулятора с СИД справедливо:
Р
IН  S
1  4 2  F 2   e2
(3.5)
Рабочая полоса частот модулятора с СИД ограничивается частотой Fmax,
на которой мощность уменьшается в 2 раз (рисунок3.5). Так как
Fmax 
1
2   e
(3.6)
для того, чтобы увеличить широкополосность модулятора, необходимо выбирать материалы с малым τе (единицы нс). Реальная полоса частот модуляции
СИД не превышает 100 МГц.
80
Р
Fmax f,Гц
Рисунок 3.5 –Частотная харктеристика модуляции с СИД
Частотная характеристика модуляции с ЛД. Все явления, которые характерны для модулятора с СИД, относятся и модуляции на ППЛ. Но модулятор с
ППЛ содержит резонатор Фабри-Перо, где помимо СПИ, присутствует СТИ.
Причем СПИ считается не информационным. Поэтому требуется некоторое
время для образования стимулированного фотона. При этом на некоторой частоте происходит одновременное образование и СТИ и СПИ. При этом Ризл
резко возрастает.
Частотная характеристика, (рисунок 3.6) обусловлена следующими явлениями:
- Сложением амплитуд СПФ и СТФ, при условии, что колебание происходит в одинаковой фазе;
- Временем создания инверсной населенности;
- Временем жизни фотонов в РФП.
Время жизни фотона - период времени с момента образования фотона до
момента времени, когда фотон попадет в ОВ. f0 – частота, на которой мощность
на выходе модулятора максимальна.
f0 
1
2
 I см 

 1
I

 порог 
е ф
(3.7)
τф – время жизни фотона (ед. пс – 5пс – стандартное значение для ППЛ);
τе – время жизни электрона, т.е. период времени, когда электрон попадает в область p-n перехода и до момента времени, когда начнется рекомбинация (ед.нс –
3 нс).
81
РиВт
Iсм1
Iсм2
Iсм3
F,Гц
Fгр
f0
Рисунок 3.6 – Частотная характеристика модуляции с ППЛ
По сравнению с СИД, рабочая полоса модулятора с ППЛ – шире.
f  0  Fгр - рабочая полоса ОМ с ППЛ, то есть это диапазон частот, где Р на
выходе модулятора остается постоянной.
Fгр  0.9  0.95  f гр для того, чтобы
F
увеличить значение гр , а именно приблизить его к f0, необходимо выбирать
сложные соединения для ППЛ; технологически совершенствовать всю конструкцию.
Обычно f0 для ППЛ с резонатором Фабри-Перо составляет 1 ГГц.
При этом:
 
I cм
I порог если β=1.02, то f = 183 МГц; β=1.1, то f = 410 МГц;
0
0
 
I cм
I порог . Но
β=1.2, то f0= 581 МГц. Это означает, брать больше отношение
при увеличении значения Iсм, амплитуда оптического импульса будет уменьшаться. Поэтому Iсм=(0.8-1.2)*Iпорог.
Другой проблемой прямой модуляции ФП-лазера стало динамическое
уширение спектра. Если лазер работает в режиме постоянного тока, то легко возникает одна продольная мода. Однако если осуществить непосредственную модуляцию, то число генерируемых продольных мод возрастает. Это связано с тем,
что одновременно с модуляцией происходит резкое изменение усиления в активном слое, и при большом числе продольных мод усиление постепенно превышает потери в резонаторе. Перераспределение мощности в модах, которое приводит к динамическому уширению спектра ЛД ФП Δλ до 10 нм при частоте модуляции 1 ГГц.
Динамическое уширение спектра зависит от частоты модуляции и затрудняет процесс передачи информационных сигналов по волоконно-оптическим линиям связи из-за хроматической дисперсии импульсов оптической мощности.
82
Данный недостаток затрудняет использование Фабри-Перо лазера на скоростях
передачи выше 622 Мбит/с.
Развитие систем передачи на основе одномодовых оптических волокон вызвало необходимость создания лазеров с распределённой обратной связью типа
DFB (Distributed Feedback Laser) с прямой модуляцией излучения и с внешней
модуляцией. В передатчиках с прямой модуляцией в соответствии с информационной последовательностью m(k) модулируется ток накачки. Например, информационная
последовательность,
рассматриваемая на
рисунке
1.11
m(k):00100110. T = 1/B.
При изменении тока через полупроводниковый диод (прямая модуляция)
меняется не только коэффициент усиления диода, но и показатель преломления
p/n перехода. Следовательно, меняется частота излучения лазера, то есть импульсы приобретают чирпинг (рисунок 3.7,а). Иными словами, проявляется паразитная частотная модуляция. При скоростях модуляции выше 1 ГГц этот чирпинг имеет положительный знак. Поэтому при использовании лазеров с прямой
модуляцией и скорости передачи в 2,5 Гбит/с (STM-16) паразитная частотная модуляция приводит к увеличению искажений, связанных с хроматической дисперсией. Поэтому по дальности передачи информации и спектральной эффективности системы связи с такими передатчиками далеки от оптимальных.
Из практических результатов использования можно отметить, что лазеры
с непосредственной модуляцией обладают эффективностью уширения спектра
того же порядка, как и SPM эффекты в ОВ и могут использоваться для трансляции цифровых сигналов со скоростями до 2,5 Гбит /с на расстояниях до 170…200
км при использовании волокна SMF-28. Для более протяженных магистралей
или при использовании более высоких скоростей передачи, потребуются уже лазеры с внешней модуляцией. Существенное улучшение технических параметров
системы связи удаётся достичь путём использования передатчиков на основе полупроводниковых лазеров с непрерывной накачкой и внешней модуляцией. Оптическая схема такого передатчика показана на рисунке 3.7,б. При применении
лазеров с внешней модуляцией импульс чирпинга не имеет. Следует отметить,
что ширина импульсов обоих лазеров одинакова, но импульс, полученный при
прямой модуляции лазера, обладает чирпингом и у него спектр шире. Для РОСлазера с модификацией резонатора максимальная частота модуляции 2,5 ГГц
ограничивается временем жизни фотонов в резонаторе.
83
а)
б)
Р
Р
t
0
T
2T
4T 5T 6T
8T
Излучение лазера
I
t
0
T
2T
T 2T
4T 5T 6T
8T
Излучение лазера
I
t
0
4T 5T 6T
t
8T
0
Накачка
T 2T
4T 5T 6T
8T
Накачка
Модулятор
P
t
0
T
2T
4T 5T 6T
8T
Модулированное излучение
лазера
Рисунок 3.7 – Модулированное излучение лазера с прямой (а)
и внешней модуляцией (б)
Временная характеристика модуляции с СИД. Пусть сигнал на входе модулятора (рисунок 3.8) поступает в импульсном виде (1).
Ic
Uд
t
(1)
t
(2)
t
(3)
0.9
0.1
Uд
τЗ1
0.9
0.1
τЗ2
Рисунок 3.8 – Определение времени включения СИД
На диаграмме (2) показано, как заряжается емкость диода. При этом так
как Uд не меняется скачками, то преобразованный сигнал задерживается на
84
время задержки τЗ1. пока Uд не достигнет своего максимума – 0.9Umax, не происходит рекомбинации носителей зарядов. Образование квантов энергии начинается спустя время τЗ2 . Поэтому отработанный оптический импульс на выходе
модулятора появляется спустя τвкл= τЗ1 + τЗ2. Скорость следования импульсов поступающего потока ограничена параметрами и характеристиками источника излучения, который располагается в передающем оптическом модуле.
Временная характеристика модуляции с ЛД. При частотах модуляции
больших, чем Fгр, модулятор с ППЛ не успевает отрабатывать эти импульсы,
поэтому возникают искажения (рисунок 3.9). Такие искажения, когда наблюдается максимальный провал мощности, называется звоном лазера. Это явление
объясняется тем, что в лазере выполняется условие инверсной населенности.
Мощность на выходе источника резко возрастает, затем, когда большая часть
электронов перейдет с уровня ЗП на уровень ВЗ. При этом подпитка другими
носителями заряда еще не осуществлена, она резко уменьшается. Такой режим
не является рабочим, так как такой сигнал в точке приема восстановить невозможно.
Ic
t,c
Pи
t, c
Рисунок 3.9 – Временная характеристика прямой модуляции на ППЛ
Кроме указанных недостатков при модуляции тока накачки лазера вносятся
шумы:
1. Шумы спонтанного излучения.
Информационным является СТИ, при этом этот вид излучения возникает на
фоне СПИ. Но так как СПИ – шум, то на выходе излучателя появляется смесь
полезного сигнала и помехи. Корректировать СПИ невозможно, поэтому уменьшить влияние этой составляющей невозможно.
2. Шумы изменения температуры и тока накачки – обусловлены изменением смещения из-за изменения температуры и модулирующих составляющих
85
тока накачки. Изменение температуры на 10С приводит к тому, что потери со-
р 
50 мкВт
10 С . Кроме того, что изменяется мощность на выходе из-
ставляют:
лучателя, так же изменяется значение Iпорог.
 T  Tmax
I порог  I по  exp 
 T0

,

(3.8)
где Т0 – температура, которая зависит от вида материла ППЛ;
Tmax - заданная температура;
Т – температура, которая показывает закон изменения окружающей среды.
I порог - значение порогового тока, при оптимальном значении температуры
окружающей среды.
3. Шумы отражения оптического сигнала от стыка с поверхностью световода связаны с возвратом отраженного света, который имеет произвольную фазу.
При этом изменяются условия генерации, которые приводят к изменению резонансной длины волны, числа генерируемых мод, изменению формы ватт-амперной характеристики.
Отраженная волна сообщает дополнительную долю энергии носителям заряда, которые не способны преодолеть ширину ЗЗ. В результате возникают новые кванты энергии, которые не несут полезной информации. При влиянии отраженной волны появляются изломы на ВтАХ. Это приводит к резкому увеличению нелинейных искажений. При этом уменьшается затухание нелинейности.
При попадании отраженной волны в ППЛ уменьшается мощность основной
моды, увеличивается ширина спектра Δλ.
Ри
Pиmax
λ
Δλ
P<Pmax
λ
Δλотр
Рисунок 3.10 – Спектральная характеристика ППЛ при отраженной волне
86
Для борьбы с шумами отражения используется оптический изолятор (вентель), который пропускает излучение в одном направлении и гасит его в обратном.
4. Шумы перескока моды возникают из-за малого спектрального расстояния между модами. При ширине спектра моды около 1-2 нм расстояние между
модами составляет около 0,8 нм. По этой причине и недостаточно высокой добротности резонатора в процессе модуляции возникают возможности генерации
лазера на соседних модах. Перескок моды приводит к значительным колебаниям
мощности излучения лазера. Для устранения шумов перескока применяется режим с высоким смещением (около или выше порогового тока).
Pи
Ри
λ
λ
Рисунок 3.11 - Переход мод
3.2 Внешняя модуляция
Внешняя модуляция основана на изменении параметров излучения при
прохождении светового луча через какую-либо среду.
Резонатор
t
Активная среда
Модулятор
t
t
Накачка
Рисунок 3.12 – Принцип внешней модуляции
В ряде материалов пропускающих оптические волны, существует возможность изменения параметров волновых процессов. Изменение достигается внешними по отношению к материалу воздействиями: изменением напряженности
электрического или магнитного поля, механическим или акустическим давлением. Все эти воздействия могут сопровождаться изменением параметров оптических волн (длины волны, интенсивности, поляризации, направления распространения). Среди эффектов внешней модуляции оптических волн наибольшее
87
применение в технике оптической связи получили электрооптический и акустооптический эффект.
3.2.1 Акустооптический эффект. Эффект Франца–Келдыша
Акустооптический эффект - это явление дифракции, преломления, отражения и рассеяния света на периодических неоднородностях среды, вызванных
упругими деформациями при прохождении акустической волны.
Акустические волны возбуждаются в веществе с помощью пъезокристалла, на который подается сигнал от генератора модулирующего сигнала с
большой акустической мощностью. Схема АОМ приведена на рисунке 3.13. При
изготовлении акустооптических модуляторов (АОМ) используются кристаллы
ТеО2 (диоксид теллура), PbMoO4 (молибдонат свинца), LiNbO3 (ниобат лития).
Поглотитель
Акусто-Оптический
Модулятор
2

лазер
Л
а
з
е
Пьезокристалл
р
Генератор
данных
Д
Рисунок 3.13 – Схема АОМ
Для описания взаимодействия света с звуковой волной в прозрачных средах необходимо знать изменение эллипса показателей преломления. В результате распространения акустической волны образуются периодические слои изменения показателя преломления, перемещающиеся со скоростью звука. Так как
скорость звука намного меньше скорости света, то в первом приближении для
задачи дифракции света можно считать слои показателей преломления неподвижными и квазистационарными, то есть за время прохода света они не успевают существенно сместиться.
Горизонтально ориентированные линии с одинаковым показателем преломления образуют дифракционную решетку. При падении на дифракционную
88
решетку световая волна будет отклоняться, если выполнены условия дифракции.
Входной и выходной лучи имеют один и тот же угол наклона к поверхности, новое направление луча имеет место только при углах Брэгга:
(3.9)
где  - длина волны света внутри АОМ, зв = v/fS, v – скорость звуковой волны
в веществе, fs – частота модулирующего сигнала.
Луч света направляется под углом Брэгга к нормали интенсивностью I0 на
входе модулятора в отсутствии дифракции, и интенсивностью Im в дифракционных максимумах при дифракции. В случае дифракции Брэгга исчезают все максимумы дифракции, кроме первого, причем в данном случае максимум первого
порядка является выходным каналам. Интенсивности световых пятен дифракции
Брэгга зависят от мощности акустических волн. Изменяя шаг решетки и ее глубину путем изменения частоты и амплитуды акустической волны, возможно,
осуществлять модуляцию света.
Из-за сложности конструкции и ограниченного спектра модулирующих
сигналов (не выше 1 ГГц) АОМ редко используются в ВОСП.
Электрооптический эффект заключается в изменении оптических
свойств некоторых материалов (например, ниобата лития LiNbO3) под действием электрического поля, создаваемого источником модулирующего сигнала.
Электрооптическая модуляция может происходить на основе линейного
эффекта Поккельса и нелинейного эффекта Керра.
Электрооптический эффект Поккельса заключается в повороте плоскости
поляризации световой волны под действием электрического поля. Нелинейный
эффект Керра появляется в зависимости показателя преломления материала от
напряженности электрического поля. Общим для указанных эффектов является
то, что внешние воздействия приводят к изменению симметрии кристалла, следствием чего является изменение его свойств. Оптически изотропные кристаллы
становятся анизотропными.
В электро-оптических модуляторах (ЭОМ) на эффекте Поккельса под воздействием модулирующего напряжения в электрооптическом кристалле ниобата
лития LiNbO3 возникает искусственная анизотропия, проявляющаяся в двулучепреломлении (рисунок 3.14).
U
Поляризатор
ЭОМ
Анализатор
ППЛ
89
Рисунок 3.14 – ЭОМ на эффекте Поккельса
Свет, распространяющийся в среде, показатели преломления которой
вдоль двух направлений различны, разделяется на обыкновенную горизонтально
поляризованную волну и необыкновенную вертикально поляризованную волну.
В результате деформации показателей преломления в различных плоскостях
кристалла между этими волнами создается набег фаз, а при интерференции двух
волн, наблюдается поворот плоскости поляризации. При максимальном модулирующем напряжении плоскость поляризации поворачивается на 90о и на выходе
ЭОМ возникает модулированное излучение.
Недостатки ЭОМ на эффекте Поккельса:
1.
Требует приложение высоких модулирующих напряжений (160-180
В).
2. Зависимость разности показателей преломления в материале от температуры.
В современных ВОСП чаще используется электрооптический модулятор
на интерферометре Маха-Цендера. Он представляет собой два встречно включенных Y – разветвителя, соединенных отрезками отдельно управляемых волноводов.
В модуляторе лазер используется только как источник света. Модуляция
происходит в одном волноводном канале, совмещенном с Y – разветвителями и
расположенном на электрооптической подложке. Электрический сигнал, подаваемый через усилитель, вызывает изменение показателя преломления волноc
n
v ПЛ . При этом в другом канале изменений нет.
водного канала
Рисунок 3.15 – ЭОМ на интерферометре Маха-Цендера
90
Оптические волны в этих каналах распространяются с разной скоростью и
приобретают разные набеги фаз, что при их сложении на выходе вызывает интерференционное уменьшение мощности. Для обеспечения высокой линейности
модуляции в схеме применяется смещение постоянным напряжением. Величина
напряжения соответствует полуволновому набегу фазы . Разность фаз обусловлена зависимостью скорости распространения волн от показателя преломления. В зависимости от  в результате интерференции двух волн во втором ответвителе формируется сигнал "1" или нуля.
При разработке интерферометра необходимо учитывать, что длина волны
на выходе интерферометра определяется по формуле:

l
 N ,
m
(3.10)
где l- длина плеча интерферометра
m – модовое число или номер моды
N – разница показателей преломления в плечах интерферометра.
ЭОМ модуляторы отличаются высоким быстродействием и получили применение в высокоскоростных системах передачи (от 2,5 Гбит/с до 40 Гбит/с).
Интегральные модуляторы на основе электрооптического эффекта реализуются в соответствии со схемой интерферометра Маха-Цендера (ИМЦ). Они состоят из двух идентичных плеч интерферометра (см. рис. 3.15а). Распространяющиеся по этим плечам моды, в зависимости от величины приложенного к электродам напряжения V длины волновода L в зоне взаимодействия полей, приобретают
*
сдвиг фаз   k m nm L , пропорциональный амплитуде изменения эффективного по-
казателя преломления моды nm  nm rE / 2 , где r - электрооптический коэффициент
рабочей оптической среды, кт - волновой вектор моды. На выходе ИМЦ происходит модуляция входного светового потока по интенсивности ввиду интерференции
достигших его мод.
*
3
91
Рисунок 3.15а – Схема электрооптического модулятора
типа интерферометра Маха-Цендера
На схеме рис. 3.15а показаны два типа электродов: электроды для создания
бегущей волны модулирующего электрического поля и статического электрического поля смещения рабочей точки на передаточной функции такого модулятора
(см. рис. 3.15б). Модулирующие электроды протяженны для создания эффективного распределенного (на длине L) взаимодействия полей электрической и оптической волн. Такое взаимодействие позволяет достичь определенного коэффициента ослабления сигнала - КОС {extinction ratio - ER) на выходе модулятора,
характеризующего достижимую глубину модуляции (порядка 20 дБ). Модулирующее напряжение приложено так, чтобы замедлить движение оптической несущей в одном плече и ускорить его в другом, что позволяет уменьшить его амплитуду V , требуемую для достижения    ; до уровня, пригодного для ИС.
92
Рисунок 3.15б – Передаточная характеристика модулятора типа ИМЦ
Передаточная функция ИМЦ представлет собой синусоиду, из которой
для управления процессом модуляции выбирают одну из полуволн, задавая определенное напряжение смещения с помощью другой системы электродов {электродов смещения). Это напряжение может быть выбрано как для работы в линейной, так и в квадратичной области передаточной функции (см. рис. 3.8).
Оптимальное конструирование и достижения интегральной оптической
технологии сделали такой тип модулятора наиболее широко используемым в
различных приложениях, и прежде всего в системах SDH и WDM. Параметры,
характерные для таких модуляторов, приведены в табл. 3.1 на примере модуляторов компании Laser2000.
Таблица 3.1. Характеристики высокоскоростных модуляторов интенсивности
типа ИМЦ
93
3.2.2 Электрооптический эффект
Если к кристаллу приложено электрическое поле, его оптические свойства
меняются. При электрооптическом эффекте наблюдается как прямое влияние
электрического поля на поляризованность кристалла, так и посредством деформации решетки. Оптические свойства кристалла без электрического поля описываются полностью тремя показателями преломления — n x , n y , n z , которые соответственно справедливы для света, поляризованного в направлении осей кристалла a  x, b  y, c  z . Чтобы установить, как ведёт себя в кристалле свет с определённым направлением распространения и поляризацией, используют эллипсоид показателей преломления с полуосями n x , n y и n z , показанный на рис. 3.16/
( x / nx ) 2  ( y / n y ) 2  ( z / nz ) 2  1
(3.11)
Рисунок 3.16 – Эллипсоид показателей преломления с эллиптическим
свечением для волновой нормали s; полуоси эллипса n1 и n1
94
Из плоскости, проходящей через начало координат, перпендикулярно направлению распространения света s, эллипсоид вырезает эллипс с полуосями n1 и
n1 . На компоненту световой волны, поляризованную линейно в направлении n1 ,
действует показатель преломления n1 , а на компоненту, поляризованную в направлении n1 действует показатель преломления n2 . Волновое число одной комk1  n1
2
k 2  n2
2
 , а другой
 . Материал преломляет свет с поляризапоненты
цией в направлении одной оси секущего эллипса, иначе чем свет с поляризацией
вдоль другой оси. Поэтому он считается двоякопреломляющим, а явление в целом называют двойным лучепреломлением.
Под действием электрического поля эллипсоид показателей преломления меняет ориентацию и величину своих полуосей. Ограничимся здесь линейным электрическим эффектом, так как практически все электрооптические модуляторы, используемые в оптической связи, работают на его основе. При линейном эффекте эллипсоид показателей преломления в электрическом поле с
компонентами E x  E1 , E y  E2 и E z  E3 получается из уравнения
( x / n x ) 2  ( y / n y ) 2  ( z / n z ) 2  k 1 (r1k x 2  r2k y 2  r3k z 2  2r4k yz  2r5k xz  2r6k xy ) Ek  1
3
.(3.12)
Коэффициенты r jk линейно зависящих от Е дополнительных членов называют электрооптическими модулями. В силу симметрии кристалла большинство
этих коэффициентов исчезает для определенного кристалла. Ненулевые коэффициенты сильно зависят от температуры и незначительно от длины волны. В табл.
3.2 даны электрооптические модули (коэффициенты) для важнейших модуляторных кристаллов при комнатной температуре на волне   1 мкм1.
Кристаллы CuCl, ZnS, GaAs и ZnTe являются кубическими, т. е. изотропными при отсутствии электрического поля с одинаковыми показателями преломления n0 для всех поляризаций. Тетрагональные кристаллы KDP, ADP и ВаТiO3,
так же как и тригональные кристаллы LiTaO3 и LiNb03, вне электрического поля
одноосны, т. е. для световых волн, распространяющихся в направлении оптической оси, они имеют не зависящий от поляризации показатель преломления п0 и
при этом отсутствует двойное лучепреломление. Во всех других направлениях
распространения показатель преломления зависит от поляризации волны. При
распространении перпендикулярно оптической оси и поляризации в направлении оси показатель преломления равен ne . Эти простейшие кристаллы имеют эллипсоид показателей преломления, симметричный относительно оптической оси
( c  z ):
( x 2  y 2 ) / n0  z 2 / ne  1.
2
2
(3.13)
95
Если кристаллы KDP и ADP модулируются электрическим полем напряженностью E z  E3 в направлении оптической оси, то эллипсоид показателей преломления преобразуется согласно
( x ' ) 2 /( n0  n) 2  ( y ' ) 2 /( n0  n) 2  z 2 / ne  1.
(3.14)
причем оси х’ и у’ повернуты относительно осей х и у на 45° в плоскости
ху. Показатели преломления для поляризаций вдоль х' и y’ больше или меньше
по сравнению с n0 на
n  n0 r63 E3 / 2.
3
Таблица 3.2. Свойства электрооптических кристаллов
96
(3.15)
97
На рис. 3.17 показано два сечения эллипсоида показателей преломления:
при наличии и отсутствии поля E3 . Для кубических кристаллов электрическое
поле в направлении оси с превращает сферическую поверхность показателей
преломления в эллипсоид вращения согласно (3.14) и (3.15); только показатель
преломления для поляризации в направлении с остается в этом случае равным n0
.
Рисунок 3.17 – Сечения эллипсоида показателей преломления для:
а) KDP, ADP; б) LiTaO3;
– – – – электрическое поле отсутствует; – – – – с электрическим полем
E z  E3
Для LiTaO3 или LiNbO3 поле напряженностью E3 , направленное вдоль оптической оси ( z  c ) , преобразует эллипсоид показателей преломления согласно
x 2 /( n0  n0 ) 2  y 2 /( n0  n0 ) 2  z 2 /( ne  ne ) 2  1,
98
(3.16)
причем n0  n 0 r13 E3 / 2, ne  ne r33 E3 / 2.
Сечения этого эллипсоида плоскостями ху и xz также показаны на рис.
3.17. Если вектор E3 направлен по оптической оси, то кристаллы LiTaO3 и
LiNbO3 остаются одноосными; для света, распространяющегося вдоль оптической оси, двойное лучепреломление отсутствует. Кристаллы KDP и ADP, наоборот, благодаря электрическому полю E3 становятся двоякопреломляющими для
волн, идущих в направлении z. На свет, поляризованный в направлении х', действует показатель преломления n0  n , а в направлении у' — показатель преломления n0  n .
3
3
3.3 Фазовая модуляция
Изменяя показатель преломления в электрическом поле, можно непосредственно модулировать фазу света. В зависимости от того, идет свет в направлении приложенного поля или перпендикулярно к нему, различают продольный и
поперечный электрооптические эффекты. Чтобы использовать продольный эффект, электроды наносят на торцевые плоскости модуляторного кристалла перпендикулярно оси с. Поскольку электроды должны быть прозрачными для света,
то их выполняют либо очень тонкими, либо в них делаются отверстия достаточной величины для светового луча, как показано на рис. 3.18, а.
При фазовой модуляции с использованием продольного эффекта в KDP
или ADP свет поляризуют в направлении одной из новых основных осей х' или
99
у'. При длине пробега L света в кристалле и продольном напряжении U  E3 L получаем сдвиг фаз
  n0 r63U /  ,
3
(3.17)
который не зависит более от длины L.
Для использования поперечного эффекта плоские электроды помещают
перпендикулярно оси с на боковых сторонах кристалла, как показано на рис.
3.18, б свет распространяется параллельно этим электродам. Фазовая модуляция
при поперечном эффекте в KDP или ADP реализуется при поляризации света
перпендикулярно оси с. Если толщина модулятора d, а поперечное напряжение
U  E3 L , то фазовый сдвиг
  n0 r63UL /( d ).
3
(3.18)
Можно увеличить сдвиг фаз при заданном напряжении, увеличив отношение сторон L/d.
В тригональных кристаллах LiNbO3 и LiTaO3 знаки величин n0 и ne одинаковы и ne  n0 . Поэтому с этими кристаллами применим только поперечный
эффект и свет должен быть поляризован в направлении электрического управляющего поля. Фазовый сдвиг в данном случае
  ne r33UL /( d ).
3
(3.19)
Коэффициент r33 для LiNbO3 и LiTaO3 в 3-4 раза больше, чем r63 для KDP
и ADP. Поэтому LiNbO3 и LiTaO3 являются наиболее эффективными модуляционными кристаллами.
3.4 Модуляторы по интенсивности
Продольный и поперечный эффекты позволяют модулировать по амплитуде
световые волны с линейной либо круговой поляризацией. Для использования продольного эффекта в KDP или ADP свет в соответствии с рис. 3.19а поляризуется
линейно в направлении х или у с помощью поляризатора. Тогда ортогональные
компоненты световых волн, направленные по осям x` и y` , движутся с разными
фазовыми скоростями. После прохождения через кристалл они оказываются свинутыми по фазе, и их суперпозиция образует эллиптически поляризованную
волну. Она попадает в анализатор, который повернут на 90° по отношению к поляризатору и пропускает поэтому только поляризацию, ортогональную исходной. Коэффициент передачи – отношение мощностей света на выходе и входе –
в таком устройстве зависит от произведения Ln следующим образом:
100
T  (1 / 2)[1  cos(4Ln /  )].
(3.20)
Рисунок 3.19 – Электрооптическая модуляция интенсивности при линейно
поляризованном свете на входе: а) модулятор (М) с поляризатором (Р) и скрещенным с ним анализатором (А); б) модуляционная характеристика при синусоидальном управлении
На рис. 3.19, б показана характеристика управления — зависимость коэффициента передачи от напряжения, определяющая при синусоидальном управляющем сигнале глубину модуляции света по интенсивности. Для малых напряжений U ~ Ln коэффициент передачи пропорционален квадрату напряжения.
101
Рисунок 3.20 – Электрооптическая модуляция по интенсивности при круговой поляризации света на входе:
а) модулятор (М) с  /4 — пластиной и анализатором (А); б) модуляционная характеристика при синусоидальном управлении
Линейную характеристику управления для малых напряжений получают,
помещая согласно рис. 3.20а между входным поляризатором и модуляционным
кристаллом четвертьволновую пластину. Благодаря своим неизменным двоякопреломляющим свойствам пластина сдвигает взаимно на 90° обе ортогональные компоненты линейно поляризованной входной волны, что превращает линейную поляризацию в круговую. Коэффициент передачи при использовании
четвертьволновой пластины
T  (1 / 2)[1  sin(4Ln /  )].
102
(3.21)
Благодаря пропорциональности Ln ~ U этот модулятор имеет характеристику управления, показанную на рис. 3.20, б. В случае малых напряжений интенсивность света меняется пропорционально управляющему напряжению. Однако при приближении глубины модуляции к 100% характеристика управления
все более отклоняется от начальной линейной зависимости. При синусоидальном
внешнем управлении вида
4Ln /   KU m sin t
(3.22)
выходная мощность света изменяется следующим образом:
P  ( P0 / 2)[1  sin( KU m sin t )].
(3.23)
Если эту функцию мощности от времени разложить по спектральным компонентам, то получаем
P  P0 / 2  P0 [ J1 ( KU m ) sin t  J 3 ( KU m ) sin 3t  ...].
(3.24)
Модулированная по интенсивности мощность помимо основного колебания с глубиной модуляции m  2 J1 ( KU m ) содержит гармоники, амплитуды которых являются бесселевыми функциями от аргумента KU m с порядком соответствующей гармоники.
Чтобы управлять передачей в пределах от 0 до 1, т. е. обеспечить 100%ную модуляцию, напряжение должно меняться на
U    /( 2n0 r63 ).
3
(3.25)
Это напряжение называют полуволновым, поскольку оно сдвигает на
180° друг относительно друга волны со взаимно ортогональными поляризциями. Полуволновое напряжение является характеристической величиной
модулятора и должно быть возможно малым для эффективной модуляции.
Если для модуляции по амплитуде или интенсивности используют поперечный эффект в KDP или ADP, то падающая волна должна быть поляризована
в плоскости x`z линейно под углом 45° к оси z либо иметь круговую поляризацию
в этой же плоскости. Мешающий сдвиг фаз, сопровождающий естественное
двойное лучепреломление благодаря ne  n0 , можно уничтожить, включив последовательно два одинаковых кристалла, оси которых повернуты взаимно на 90°, а
управляющие напряжения, определенные в положительных направлениях
осей с, находятся в противофазе.
103
Для компенсации естественного двойного лучепреломления можно установить полуволновую пластину между двумя одинаково ориентироваными кристаллами и изменять оба напряжения в противофазе. Полуволновое напряжение
при поперечных AM и МИ равно
U    (d / L) /( n0 r63 ).
3
(3.26)
При d=L оно в 2 раза больше, чем для продольной модуляции, однако может быть понижено уменьшением d/L.
При AM либо МИ с использованием поперечного эффекта в LiNbO3 или
LiTaO3 падающая волна должна быть поляризована под углом 45° к оси с. Тогда полуволновое напряжение
U    (d / L)(ne r33  n0 r13 ).
3
3
(3.27)
Разность фаз между волнами двух поляризаций в направлении оси с и перпендикулярно ему зависит только от разности ne — n0 . Несмотря на это, полуволновые напряжения для LiNbO3 и LiTaO3 намного меньше, чем для KDP и
ADP, так как определяющий модуляцию электрооптический модуль намного
больше.
3.5 Параметры, полоса и мощность модуляции
Если не учитывать диэлектрические потери и потери на утечку в модуляторных кристаллах, то электрооптические модуляторы, изображенные на рис.
3.18, 3.19 и 3.20, не потребляют модуляционной мощности. Однако энергия
накапливается и в их электрических полях, что приводит к возникновению реактивной мощности. Объёмная плотность энергии равна E 2 / 2 , поэтому запас
энергии и реактивная мощность тем больше, чем выше диэлектрическая проницаемость модуляционного кристалла. В таблице 3.1 приведены значения диэлектрических проницаемостей кристаллов в двух направлениях: параллельно и перпендикулярно оси c. Для оценки их пригодности для модуляторов сравним
между собой полуволновые напряжения кристаллов и запасы энергии при этих
напряжениях. Ограничимся при этом поперечными модуляторами и отнесём U 
к отношению сторон d/L, т.е. рассчитаем приведенное полуволновое напряжение
u  U  ( L / d ).
(3.28)
В качестве характеристики запасенной энергии используем
   U  ( L / d ).
Оба этих параметра приведены в табл. 3.1 для  = 1 мкм.
104
(3.29)
Чтобы сделать низким полуволновое напряжение при модуляции с применением поперечного эффекта, отношение сторон d/L должно быть минимально
возможным. Нижняя граница этого отношения устанавливается поперечным
расширением световой волны. При свободных лучевых волнах по возможности
используют только гауссовы пучки; их фокусируют на модуляторе таким образом, чтобы длина L модулятора в точности равнялась отрезку между линзами в
конфокальной линзовой линии. При этих условиях можно выбрать
d 2 / L  s 2 4 /(n),
(3.30)
где s — коэффициент запаса, определяющий отношение d к радиусу пятна w лучевой волны. Практически для уменьшения дифракционных потерь и легкой юстировки выбирают s>2.
Ширина полосы модуляции ограничивается оптической длиной nL модулятора и его реактивной проводимостью C . Если время пробега волны t 0  nL / c
не мало по сравнению с периодом T  2 /  высшей частоты модуляции, модуляционный сдвиг уменьшается пропорционально коэффициенту зазора
(sin / 2) /( / 2), где   2t 0 / T – угол пролёта модулятора. Лишь при   2 на
световой пучок действует примерно одинаковое модуляционное напряжение за
всё время пробега. При   2 обе полуволны модуляционного колебания в точности компенсируются и модуляция отсутствует. Коэффициент зазора уменьшается до 1 / 2 , когда частота модуляции доходит до
t  2,8c /( nL);
(3.31)
назовём её граничной частотой модуляции вследствие конечного времени пробега.
Ограничение полосы модуляции реактивной проводимостью C определяем по электрической эквивалентной схеме, приведенной на рис. 3.21. Напряжение U модуляционного генератора с внутренним сопротивлением нужно
трансформировать в требуемое для модулятора напряжение uU. Для низких модуляционных частот можно считать, что параллельно модулятору включено сопротивление u 2 R . Из-за параллельной ёмкости напряжение модуляции падает с
ростом частоты.
105
Рисунок 3.21 – Эквивалентная электрическая схема
электрооптического модулятора
При
c  2 /(u 2 RC )
(3.32)
оно составляет только 1 / 2 часть своего значения на низших частотах.
Уравнение (3.22) определяет граничную частоту модуляции при шунтировании
емкостью. При заданной величине С можно повысить c , снижая u 2 R , однако в
той же мере возрастет мощность
Pm  U m /( 2u 2 R)  cCU m / 4,
2
2
(3.33)
которую нужно затратить для получения определённой амплитуды модуляции U m . Для модуляции интенсивности света согласно рис. 4.11 от 0 до полной
интенсивности нужно, чтобы U m  U  / 2 . При квадратном сечении модуляционного кристалла и размерах, соответствующих (3.30), мощность модуляции
Pm / f c  s 2  /( 2n).
(3.34)
Мощность модуляции, отнесенная к полосе модуляции, непосредственно
определяется параметром  для запасенной энергии. Значение такой нормированной мощности модуляции, вычисленные для s  4 и   1 мкм, приведены в
табл. 4.2.
3.6 Электроабсорбционные модуляторы
Последний тип модуляторов света по интенсивности в последнее время
находит все большее применение. Связно это, во-первых, с малыми величинами
напряжений, необходимых для осуществления почти 100% модуляции, во-вторых,
такой модулятор легко интегрируется в одной конструкции вместе с лазерным кристаллом, оптическим изолятором и остальными элементами волоконной оптики. На
106
рис. 3.22 приведена схема устройства этого лазера. На лазерный волноводный кристалл. 1 нанесена дифракционная решетка Брэгга 2. Непосредственно к нему примыкает входная грань электроабсорбционного модулятора 3. На верхней грани устройства нанесен электропроводящий слой (электрод) 3 для подвода электрического тока
к лазерному кристаллу.
Рисунок 3.22 – Схема полупроводникового лазера с решеткой Брэгга
и внешним модулятором:
1 - лазерный волноводный слой (MQW); 2 - решетка Брэгга; 3 - электрод;
4 - полупроводниковый изолятор РР; 5 - электрод для внешнего модулятора;
6 - волноводный электроабсорбционный модулятор; 7 - выходное окно
с антиотражающим покрытием; 8 - период решетки Брэгга; 9 - подложка;
I íàê  - постоянный ток накачки лазера; U - модулирующее напряжение
мод
Для подключения модулирующего электрического сигнала к ЕА (электроабсорбционный модулятор) в правой части (над ЕА) также нанесен электропроводящий слой 5. Электроды 3 и 5 изолированы друг от друга полупроводниковым
изолятором 4 из InP. Модулированное по интенсивности излучение выходит че-
107
рез окно 7, поверхность которого покрыта антиотражающим слоем. Перечисленные элементы размещены на подложке 9, выполненной из материала n - InP.
Лазерный кристалл выполнен из химического соединения InP/ InGaAsP. Лазер
предназначен для работы в ЗОП в диапазоне 1530... 1565 нм. Благодаря примененной структуре и температурной стабилизации долгосрочная стабильность
длины волны составляет 0,01 нм (в течение 20 лет).
Работа лазера возможно также в L-диапазоне 1560…1620 нм. Величина
порогового тока Iпор = 10 мА, средний уровень выходной мощности Pâûõ  3
дБм. Для получения модуляции с коэффициентом экстинкции (коэффициент модуляции), равным 8,2 дБ (стандартная величина), требуется напряжение с двойной амплитудой 2 В (или амплитудой импульса). В данном типе модулятор почти полностью прозрачен при U ìîä  0 . Данный ЕА допускает частоту модуляции
более 12,5 ГГц, но в ближайшем будущем она будет повышена до 50 ГГц.
108
4 КОМПОНЕНТЫ ДЕТЕКТИРОВАНИЯ ОПТИЧЕСКОГО ИЗЛУЧЕНИЯ
4.1 P-i-n фотодетекторы
В ВОСП в качестве приемных устройств используются полупроводниковые фотодиоды (ФД). Фотодиод преобразует оптическую энергию в электрическую. ФД в наибольшей степени удовлетворяют предъявляемым требованиям к
фотоприемным устройствам оптических систем.
Наибольшее применение в ВОСП получили p-i-n фотодиоды (PIN), лавинные фотодиоды (ЛФД, APD). В быстродействующих фотоприемниках с полосой
частот до нескольких гигагерц применяются фотодиоды (ФД) с pin-структурой и
лавинные фотодиоды (ЛФД).
Требования к фотоприемным устройствам ВОСП:
1. Для получения эффективного оптоэлектронного преобразования спектральные характеристики фотоприемника и источника должны быть согласованы.
2. При преобразовании фотоприемник должен вносить минимально возможные шумы и искажения, то есть иметь низкий уровень шумов, обладать требуемой чувствительностью, быстродействием и динамическим диапазоном.
3. Конструкция фотоприемника должна обеспечивать надежное соединение с оптическим волокном.
4. Длительный срок службы и возможность использования в интегральных схемах.
4.2 Принцип действия фотодиодов
Принцип действия любого фотодиода основан на внутреннем фотоэффекте, который заключается в увеличении электропроводности вещества при
его освещении. В фотопреобразовательном режиме последовательно с ФД включается внешний источник энергии, смещающий диод в обратном направлении.
Р-i-n фотодиод имеет трехслойную структуру: высоколегированные области p+, n+ с большой концентрацией свободных носителей (дырок и электронов)
и сравнительно протяженный обедненный носителями (слабо легированный) i–
слой. Легирование примесями по заданному профилю обеспечивает характерное
распределение потенциалов, при котором все прикладываемое к ФД напряжение
сосредоточено в i-слое. для повышения эффективности преобразования фотонэлектрон необходимо, чтобы фотоны попадали в i-слой.
Если на фотодиод не воздействуют фотоны, то в его структуре протекает
слабый темновой ток, обусловленный тепловыми движениями зарядов. Темновой ток ограничивает уровень минимально детектируемой мощности сигнала.
109
При падении фотонов на i-слой происходит генерация свободных носителей (электронов и дырок), так как кванты света выбивают электроны из валентных связей полупроводника. Время жизни носителей, образованных в i-слое,
намного превышает их время жизни в p- и n- слоях (где они быстро рекомбинируют). Носители, под воздействием высокого напряжения обратного смещения,
быстро смещаются к границам обедненной зоны, при этом замыкается цепь и
начинает протекать фототок.
Рисунок 4.1 – Структура p-i-n фотодиода
Фототок Iф0, если ЕфЕg. Оптический сигнал считается преобразованным
в электрический, если выполняется соотношение ргр, где р - рабочий диапа гр 
hc
Е g - определяет длинноволновую границу чувствительно-
зон длин волн,
сти фотодиода.
гр – длина волны, до которой оптический сигнал может быть преобразован
в электрический, так как при превышении пороговой длины волны энергии фотона
ЕФ 
hc
 не достаточно для возникновения фотоэффекта.
Структура ЛФД дополнительно содержит слаболегированный слой p-. К
ЛФД подводится высоковольтное питающее напряжение, близкое к напряжению
пробоя. Профиль примесей обеспечивает условия, при которых напряжение максимально сосредоточено в р- слое. При возникновении носителей в i-слое, электроны в р- слое с высоким ускоряющим напряжением, соударяются с узлами кристаллической решетки и в результате ударной ионизации выбивают дополнительные электроны. (Носители в сильном электрическом поле приобретают избыточную энергию, достаточную для создания новых пар носителей зарядов за
110
счет ударной ионизации). В результате в переходе вблизи пика напряженности
поля происходит умножение носителей. Поскольку вновь появившиеся носители
в свою очередь способствуют ударной ионизации, то число носителей лавинообразно увеличивается, что вызывает усиление фототока.
Коэффициент умножения фототока определяется из соотношения:
М
1
V 
1   
 VB 
m
,
( 4.1)
где VB – напряжение пробоя ЛФД;
V – напряжение смещения, подаваемое на ФД;
М – характеризует чистоту полупроводника.
Коэффициентом М трудно управлять, так как он зависит от температуры и
напряжения . Поэтому эти параметры необходимо жестко стабилизировать.
Рисунок 4.2 – Структура ЛФД
4.3 Основные характеристики фотодиодов
111
1. Токовая чувствительность SТЧ определяется отношением фототока к
оптической мощности
I  А 
SТЧ  Ф 
Р( )  Вт 
Для p-i-n фотодиода SТЧ=0,50,9 А/Вт
Для ЛФД SТЧ=2060 А/Вт
SТЧ задается на длине волны, соответствующей максимуму чувствительности для определенного окна прозрачности волокна.
2. Внутренняя квантовая эффективность вн – это безразмерная величина, определяющая соотношение числа электронов и фотонов в фотодиоде.
N
 ВН  Э 1
Nф
При расчете вн не учитываются отраженные фотоны, а для ЛФД дополнительно не учитываются электроны, возникающие при ударной ионизации.
Для pin ФД вн=0,30,5
Для ЛФД вн= 0,60,8
Фототок определяется как:
IФ  NФ *в н * е ,
19
где е  1,6 *10 Кл - заряд электрона.
Темновой ток – это ток, протекающий через нагрузку обратно смещенного
фотодиода в отсутствии светового потока. Этот ток вызывается электронами, перешедшими под влиянием температурных изменений из валентной зоны в зону
проводимости. Поэтому, чем меньше величина энергии запрещенной зоны, тем
больше величина Iт.
Для pin ФД IТ=0,110 нА
Для ЛФД IТ=30100 нА.
Uпит
Рисунок 4.3 – Вольт-амперные характеристики p-i-n фотодиода
3. Быстродействие фотодиода определяется временем нарастания электрического сигнала Н.
Будем считать, что в идеале поступает оптический импульс прямоугольной
формы. Импульс считается отработанным, когда его амплитуда увеличиться от
112
0.1 Iф/Iфmax до 0.9Iф/Iфmax (рисунок 4.4).
Для pin ФД Н=0,1-5 нс
Для ЛФД Н=0,01-1 нс.
Рисунок 4.4 – Характеристика быстродействия ФД
4. Широкополосность определяется на уровне 0,707 от максимальной
спектральной чувствительности.
Рисунок 4.5 – Спектральная характеристика ФД
Неравномерность характеристики на коротких длинах волн обусловлена
шунтирующим действием барьерной емкости р-n перехода, а в длинноволновом
диапазоне граничной длиной волны.
113
Спектральная чувствительность фотодиодов определяется типом полупроводниковой структуры, при этом красная граница фотоэффекта составляет:
- для Si –ФД Р=800-1100 нм
- для Ge – ФД Р=1100-1700нм
5. Напряжение смещения Uд– напряжение подаваемое на ФД.
Для pin ФД Uд=10-30 В.
Для ЛФД Uд=100-400 В.
4.4 Лавинные фотодиоды
ФД с pin-структурой состоит из п+-подложки, слаболегированного слоя (iслоя) и тонкого Р+-СЛОЯ толщиной до 0,3 мкм. При приложении обратного
смещения обедненный слой распространяется на весь i-слой собственной проводимости. В результате уменьшается емкость перехода, расширяется область поглощения света и повышается чувствительность ФД. Падающий свет,
затухая по экспоненциальному закону в зависимости от значения коэффициента
поглощения α, вызывает появление фотовозбужденных носителей заряда. Фотовозбужденные носители, появившиеся в обедненном слое, ускоряются электрическим полем обедненного слоя (≥103В/см) до скорости насыщения дрейфа
(~107 см/с). Эту область называют областью дрейфа. Так как фотовозбужденные
носители за пределами обедненного слоя в р+- и п+-слоях движутся за счет диффузии, то их скорость движения, равная ≈104 см/с, оказываетя на три порядка
ниже скорости дрейфа. Этот диффузионный ток является причиной ухудшения
быстродействия ФД, которое проявляется в виде «хвоста» импульсной
характеристики. Поскольку эти фотовозбужденные носители перемещаются на
расстояние порядка диффузионной длины и рекомбинируют, то тем самым
уменьшается квантовый выход. Чтобы одновременно удовлетворить требованиям быстродействия и высокого квантового выхода, необходимо, чтобы область поглощения света находилась в обедненном слое. Для этого при проектировании фотодиода делают р+-слой как можно тоньше, а толщину i-слоя выбирают большей длины поглощения света (величина 1/α). При этом, как показано
на рис. 4.6, длина поглощения для кремния на длине волны 0,8 мкм составляет
10–20 мкм, а величина рабочего напряжения, необходимая для получения
достаточно широкого обедненного слоя, оказывается сравнительно низкой –
порядка 10–20 В.
В ЛФД обедненный слой, возникающий при приложении обратного
напряжения, также необходимо рассматривать как область поглощения света;
однако для создания ударной ионизации с помощью фотовозбужденных носителей рядом с рn-переходом создают область с высоким значением напряженности
электрического поля (более 105 В/см), которую рассматривают как область лавинного умножения. Если фотовозбужденные носители, возникшие в результате
114
поглощения света в области дрейфа, инжектировать в область лавинного умножения, то под действием непрерывной ударной ионизации возникнет лавинное
умножение фотовозбужденных носителей. Обычно ЛФД, благодаря эффекту лавинного умножения, обладают большей чувствительностью по сравнению с
обычными ФД. Если напряжение смещения обозначить через V, а напряжение
пробоя – через VB. то коэффициент умножения М приближенно может быть
представлен эмпирической формулой Миллера (см. формулу (4.1)).
Рисунок 4.6 – Зависимости коэффициента поглощения и длины поглощения
от длины волны
Он принимает различные значения в зависимости от напряжения смещения. При V≈VB с повышением напряжения происходит резкое увеличение коэффициента умножения, который может принимать высокие значения порядка
115
M=1000. С другой стороны, коэффициент умножения сильно изменяется при изменении напряжения и температуры, что является недостатком. При этом температурный коэффициент изменений напряжения пробоя составляет ≈0,2%/°С. В
схеме смещения ЛФД необходимо предусмотреть меры, которые бы устраняли
влияние этих изменений.
На рис. 4.7 приведены конструкции ЛФД и pin-ФД. Эти конструкции могут
изменяться в зависимости от свойств материалов. Для предотвращения отражения света от поверхности все ФД покрываются просветляющей пленкой. Защитное кольцо по периметру pn-перехода служит для повышения напряжения пробоя, предупреждения локального лавинного пробоя (микроплазмы) и осуществления равномерного лавинного усиления. В кремниевом ЛФД из-за расширения
обедненного слоя до 20 мкм и более рабочее напряжение падает. Поэтому область обедненного слоя формируют в виде р-(π)-слоя низкой концентрации, а лавинную область, требующую большой напряженности электрического поля, –
как р-слой с высокой концентрацией носителей. На рис. 4.2, а приведена конструкция ЛФД со структурой n+πpπp+ и n+pπp+. В первом случае умеренным сдерживанием напряженности электрического поля в области лавинного умножения
оказывается возможным получить широкий обедненный слой с высоким квантовым выходом.
116
Рисунок 4.7 – Конструкция ЛФД и pin-ФД: а –кремниевый ЛФД; б –
GaInAs-ЛФД; в – германиевый ЛФД; г – р/п-ФД. 1 – просветляющая пленка; 2 –
электрод (омический контакт); 3 – защитное кольцо; 4 – изоляция
При этом напряжение пробоя оказывается низким, а быстродействие – высоким. Например, при VB=100–150 В быстродействие оказывается равным приблизительно 300 пс. В Ge, как видно из рис. 4.6, на длинах волн, меньших 1,5
117
мкм, значение α оказывается высоким и равным 104 см-1, а длина поглощения
становится ниже нескольких микрометров. Поэтому в Ge ЛФД не требуется широкого обедненного слоя, как в Si ЛФД, и он может быть выполнен в виде простой р+n-структуры, как показано на рис. 4.7, в. Однако на длинах волн, близких
к 1,55 мкм, α уменьшается и возникает необходимость в расширении обедненного слоя, поэтому ФД изготавливают в виде р+nπn-структуры. Напряжение пробоя при этом составляет порядка 30 В, а быстродействие – порядка 200– 250 пс.
В GalnAs ЛФД рn-переход отделен от области погло щения света и сформирован
внутри слоя InP-диафрагмы. Лавинное умножение осуществляют внутри InP.
Это связано с тем, что в pn-переходе в GalnAs легко возникает туннельный пробой. Диапазон воспринимаемых длин волн лежит в пределах 0,95–1,65 мкм, а
квантовый выход составляет 70–80%.
Рисунок 4.8 – Характеристика спектральной чувствительности фотоприемника.
118
4.5 Характеристика спектральной чувствительности
Если мощность оптического излучения обозначить через р0 то число падающих фотонов будет равно p0/hv, а число носителей, возбужденных этими квантами света, составит IР0, где IРо – фототек. Следовательно, если квантовый выход
обозначить через η, то
(4.2)
Квантовый выход η представляется в виде следующего простого выражения:
(4.3)
где La – ширина области поглощения света.
По мере уменьшения коэффициента отражения от поверхности кристалла
и увеличения ширины области поглощения света по сравнению с длиной поглощения повышается квантовый выход. На рис. 4.3 приведен пример спектральной
чувствительности фотоприемника. Граница чувствительности в области больших длин волн определяется шириной запрещенной зоны материала Еg, a падение чувствительности в области коротких волн объясняется уменьшением длины
поглощения, поглощением света вблизи поверхности и возрастанием потерь за
счет поверхностной рекомбинации фотовозбужденных носителей. При наличии
слоя диафрагмы с большим значением ширины запрещенной зоны, как, например, в GalnAs ЛФД, можно получить почти постоянную чувствительность
вплоть до края поглощения в слое диафрагмы.
4.6 Быстродействие
Быстродействие ограничено временем пробега фотовозбужденных носителей и постоянной времени RC-цепочки. В области дрейфа скорость дрейфа достигает ~ 107 см/с, так что время пробега при ширине обедненного слоя 100 мкм
оказывается небольшим, около 1 нc. При ширине несколько десятков микрометров и ниже получается быстродействие порядка нескольких ГГц. Электростатическая емкость определяется суммой паразитной емкости корпуса и емкости перехода, зависящей от диаметра фотоприемной части и обедненного слоя. Она составляет 1–2 пФ. Следовательно, если сопротивление нагрузки положить равным
50 Ом, то постоянная времени RС-цепочки будет составлять 50–100 пс. Однако
при увеличении сопротивления нагрузки с целью повышения отношения сигнал/шум происходит снижение быстродействия.
В дополнение к этому следует заметить, что в ЛФД быстродействие ограничивается также временем пробега в области лавинного пробоя τeff и коэффициент умножения M(f) принимает вид
119
(4.4)
где Mo – коэффициент умножения при постоянном токе.
Ширина полосы fс, при которой M2(f)=M20/2, равняется
(4.5)
и уменьшается обратно пропорционально коэффициенту умножения. В
кремниевом ЛФД при M=100 fc оказывается порядка 1,5 ГГц. Произведение
teitMo можно рассматривать как время нарастания коэффициента умножения,
необходимое для достижения им значения М0 в результате повторяющейся ударной ионизации.
120
Рисунок 4.9 – Темновой ток фотоприемников (площадь фотоприемной части
4•10-5 см2) в зависимости от ширины запрещенной зоны Еg, эВ
4.7 Темновой ток и шум лавинного умножения
Ток, протекающий в фотоприемнике независимо от фототока, называется
темновым током. Темновой ток представляет собой сумму обратного тока I d,
протекающего через переход, и тока поверхностной утечки ISL. Так как темновой
ток вызывает дробовой шум и тем самым ухудшает отношение сигнал/шум, то
желательно, чтобы он был возможно меньшим. На рис. 4.9 приведены зависимо-
121
сти измеренных значений темнового тока от ширины запрещенной зоны материала в области поглощения, полученные для различных фотоприемников. Из рисунка видно, что при увеличении ширины запрещенной зоны уменьшается составляющая Id, и поэтому темновой ток резко падает.
Дробовой шум возникает при образовании фотоносителей за счет поглощения квантов света, а также в процессе лавинного умножения в ЛФД. Поэтому
среднеквадратичное значение полного тока фотоприемника, обусловленного
дробовым шумом, будет представляться в виде
(4.6, 4.7)
где F(M) – коэффициент шума лавинного умножения (коэффициент избыточного
шума), Bf – ширина полосы пропускания усилителя, k – отношение коэффициентов ионизации электронов и дырок; знаменатель представляет собой коэффициент ионизации носителей, инжектированных в область лавинного умножения. В
случае фотодиода в вышеприведенной формуле можно положить М= 1.
122
Рисунок 4.10 – Зависимость коэффициента шума лавинного умножения F(M)
от коэффициента умножения М
123
124
Рисунок 4.11 – Зависимость коэффициента ионизации электронов α, коэффициента ионизации дырок β и их отношения k от напряженности электрического поля.
Так как в процессе лавинного умножения число столкновений ограниченно, то коэффициент лавинного умножения достигает некоторого предельного
значения, а статистический разброс числа столкновений проявляется в виде дробового шума (шума лавинного умножения). Величина шума лавинного умножения определяется F(M). На рис. 4.10 приведены характеристики F(M), вычисленные по формуле (4.7), из которых видно, что F(M) возрастает с увеличением коэффициента лавинного умножения, но в целом имеет более низкий уровень в материалах с меньшим значением отношения коэффициентов ионизации. Поэтому
для уменьшения шума необходимо, чтобы разность между коэффициентом
ионизации электронов α и коэффициентом ионизации дырок β была по возможности большей и чтобы носители, инжектированные в область лавинного умножения, обладали большим коэффициентом ионизации. На рис. 4.11 приведены
зависимости коэффициентов ионизации а, β и отношения k – коэффициентов
ионизации носителей, инжектированных в Si, Ge и InP, от напряженности электрического поля. В кремнии область лавинного умножения формируется инжекцией электронов в р-область при α>β Коэффициенты ионизации α, β сильно зависят от напряженности электрического поля. Кроме того, по мере снижения
напряженности разность между α и β возрастет. Поэтому для уменьшения шума
желательно иметь умеренно низкую напряженность электрического поля области лавинного умножения.
В кремнии темновой ток небольшой, порядка 10-12 А, и при k в пределах
0,05–0,1 шум лавинного умножения тоже невелик. Ge ЛФД в области больших
длин волн характеризуется большим значением темнового тока, значением k,
близким к единице, а также большим шумом лавинного умножения. Все это
ограничивает возможность уменьшения уровня шума. Поэтому в настоящее
время ведется разработка GalnAs ЛФД, в которых значение k примерно такое,
как у InP.
125
5 КОМПОНЕНТЫ ВОЛОКОННО-ОПТИЧЕСКИХ ТРАКТОВ
5.1 Диэлектрический пленочный волновод
Начнем с рассмотрения диэлектрического пленочного волновода,
анализ которого относительно прост, а многие свойства одинаковы с другими оптическими волноводами. Такие волноводы применяются в компонентах и схемах оптических систем связи. Как показано на рис. 5.1, они
состоят из тонкой пленки 1 с малым оптическим поглощением и показателем преломления
, которая лежит на прозрачной подложке 2 с меньшим
показателем преломления . Над пленкой находится среда 0, обычно свободное
пространство, с показателем преломления =1.
Смотря по тому, испытывает ли однородная плоская волна преломление
либо полное отражение, что зависит от угла наклона луча , различают три вида
волн.
Пространственная волна может приходить из пространства 0. Так как
> > , то она не отражается полностью ни на одной из граничных поверхностей. Такие пространственные волны могут также приходить из подложки или
от любого источника, находящегося в пленке; для них характерен только угол
падения
превышающий граничный угол полного отражения на границе
пленки и внешнего пространства.
Рисунок 5.1 – Пленка на подложке с траекторией лучей
различных видов волн
Волны подложки могут приходить из подложки; после преломления в
пленке их угол падения настолько мал, что на границе со свободным пространством они полностью отражаются. Однако эти волны могут быть также возбуждены источниками в пленке.
126
Для волн пленки угол настолько мал, что они полностью отражаются от
обеих границ. Только эти волны связаны с пленкой, и их поля уменьшаются экспоненциально как в подложке, так еще сильнее во внешнем пространстве. В отличие от них, волны подложки излучаются через подложку, а пространственные
волны – как во внешнее пространство, так и в подложку. Полезны и важны
только волны пленки. Волны подложки и пространственные волны являются паразитными, создающими нежелательные и мешающие поля излучения, которых,
однако, часто нельзя избежать при возбуждении волн пленки; они образуются
также на неоднородностях при распространении волн пленки и вызывают потери
и интерференционные помехи.
Пространственная волна и волна подложки могут иметь любой угол
в
соответствующем им диапазоне углов. В этом смысле они образуют континуум
– непрерывное множество волн. Волны пленки, наоборот, могут иметь в области
<arccos( ) только конечное число дискретных значений. Рисунок 5.2 поясняет происхождение этих дискретных значений.
Волна пленки состоит из однородной плоской полны, которая полностью отражается от границ под углом
и движется по зигзагу. На рис. 5.2
показаны типичная траектория луча ABCD и фазовые фронты (штрихпунктиром), принадлежащие однородной
B
F
D
Рисунок 5.2 – Зигзагообразный путь и фазовые фронты волны пленки
плоской волне, движущейся от A до В и от С до D. Чтобы получилось
самоподдерживающееся распределение поля для волны пленки, однородная плоская волна после двух полных отражений должна совпасть по фазе
с первоначальной. Фазовый фронт BE на пути E F должен перейти в тот же
фазовый фронт FC, как и по окольному пути ВС с двумя отражениями – в
B и С. Поэтому разность фаз между этими путями может быть только 2тπ
(при целом m). Обозначив через Ф n и Ф c сдвиг фаз при отражениях в точках
В и С, запишем это условие:
k 1 (EF–ВС)+ Фв + Фс= -2тπ,
(5.1)
где BC=d/sin ; EF=BFcos ; BF=d/tg -dtg ,; d – толщина пленки.
Уравнение (5.1) называется характеристическим или уравнением собственных значений для волн пленки тех значениях углов , которые являются его решениями, однородные плоские волны движутся по зигзагообразному пути в пленке; их наложение образует волну пленки. Из-за фазо-
127
вых углов Ф в и Ф c в (5.1) однородные плоские волны различных поляризаций должны различаться. Волны пленки, образующиеся при сложении волн
с магнитным полем в плоскости падения, называются Н-волнами, так как
только магнитное поле имеет компоненту в направлении распространения.
Подставляя Ф  , вместо Ф в и Ф c в (5.1), получим характеристическое уравнение для этих волн:
arctg ( V / U ) + arctg ( W / U ) = U - тπ,
(5.2)
где поперечные компоненты векторов k обозначены следующим образом:
(5.3)
Характеристическое уравнение может быть упрощено, если отказаться от учета числа целых периодов в разности фаз и определить тангенсы от обеих частей (5.2):
(5.4)
Другая поляризация элементарных волн с электрическим полем, лежащим в плоскости падения, приводит к волнам пленки, называемым Еволнами, так как только электрическое поле имеет компоненту в направлении распространения. Чтобы получить их характеристическое уравнение,
следует конкретизировать Ф в и Ф c с помощью Ф || ; это приводит к
2
2
2
2 2 2
4
tg U= n1 U (n0V  n2W ) /(n0 n2U  n1 VW ) ,
(5.5)
Одно из характеристических уравнений совместно с тремя соотношениями (5.3) между поперечными постоянными фазы или затухания, U, V,
W, и коэффициентом фазы β в направлении распространения образует систему из четырех уравнений, решение которой для каждого числа т соответствует определенной волне пленки. Эти волны различаются числом т и
обозначаются соответствующими индексами Н т - или E m -волны. Система
уравнений трансцендентна и поэтому в общем случае решается только численно.
Рассмотрим решение указанной системы уравнений для имеющего
практическое значение случая, когда показатели преломления п 1 и п 2
пленки и подложки различаются лишь незначительно, в то же время они
значительно больше, чем показатель преломления п 0 верхнего полупространства. Такие соотношения выполняются, например, в случае, когда на
128
стеклянную подложку осаждают стеклянную пленку, оптически лишь несколько более плотную, а пространство снаружи оставляют свободным.
При этих условиях граничный угол
полного отражения между пленкой
и подложкой очень мал; величина U по (5.3) также остается очень малой
для всевозможных значений <, поэтому β только незначительно отличается от
и . Очевидно, что V очень мало, в то время как W очень велико
по сравнению с U и V . Тогда оба характеристических уравнения упрощаются и приводятся к виду не содержащему ни W , ни показателей преломления.
(5.6)
Рисунок 5.3 – Графическое решение характеристического
уравнения для слабо направляющей пленки
На рис. 5.3 дан график V как функции от U в соответствии с (5.6). Представляет интерес только первый квадрант, так как волны пленки имеют только
положительные вещественные значения U и V. Из (5.3) следует соотношение для
суммы квадратов
, соответствующее на плоскости U-V
кругу радиусом
R=2π
d/λ.
(5.7)
Точки пересечений ветвей кривой с этим кругом являются решениями системы уравнений и соответствуют волнам пленки.
Наряду с поперечными постоянными волны U и V , описывающими
распределения ее поля в пленке и подложке, важно определить коэффициент фазы  как меру продольного распространения волны пленки. Удобно
представить  с помощью нормированного коэффициента фазы
129
(5.8)
Учитывая, что B=V 2 /R 2 согласно (5.3), его можно представить как
функцию параметра R. Для слабонаправляющей пленки с п 1 п 2 величина
В равна разности между β и волновым числом подложки, деленной на разность волновых чисел пленки и подложки:
B
,
(5.9)
На рис. 5.4 нормированный коэффициент фазы В показан в функции
от параметра R для различных волн пленки. Радиус R зависит от длины
волны λ либо частоты света, а также от всех существенных параметров слабонаправляющей пленки, а именно толщины пленки d и показателей преломления п 1 , п 2 пленки и подложки соответственно.
Рисунок 5.4 – Нормированный коэффициент фазы
слабонаправляемых волн пленки
При R<π/2 волн пленки не существует. Только когда частота или Разность показателей преломления становится настолько большой, что R>π/2,
круг радиусом R впервые пересекает ветвь кривой. Это решение ур-ния
(5.1) для т = 0; оно описывает H 0 - и E 0 -волны. На граничной частоте либо
при граничной толщине, соответствующих R = π/2, нормированный коэффициент фазы β вначале равен волновому числу подложки; с увеличением
R он приближается к волновому числу пленки. На граничной частоте R =
π/2) U = π /2 и V = 0, при этом поперечное распределение электрического
поля для H 0 -волны или магнитного поля E 0 -волны внутри пленки имеет
форму четверти синусоидальной волны с максимумом на границе с подложкой. Поля в подложке при V = 0 постоянны и простираются произвольно далеко, что соответствует границе полного отражения. С ростом
частоты (R>π/2) согласно рис. 5.3 увеличиваются также U и V , однако V
130
стремится к бесконечности, a U – к π. При этом поля все меньше проникают в подложку и при высоких частотах полностью концентрируются в
пленке, где их распределение принимает форму полуволны.
На рис. 5.5 а показано поперечное распределение поля H 0 (E 0 )-волны
для средних значений R>π/5. На рис. 5.5 б и в показаны поперечные распределения полей Н 1 ( Е 1 ) - и Н 2 ( Е 2 ) -волн. Эти волны пленки высших порядков появляются, когда R>3π/2 или R>5π/2 и круг на рис. 5.3 пересечет
следующие ветви кривой. В уравнении (5.1) этим решениям соответствует
m = 1 или m = 5.
Рисунок 5.5 – Поперечные распределения полей E(H)
слабонаправляемых Em(Hm)-волн пленки
Порядок m волны пленки равен, таким образом, числу нулей в поперечном
распределении поля. Распределение поля в подложке и коэффициент фазы высших волн пленки изменяются в промежутке от их граничных частот до весьма
высоких частот так же, как у H 0 (E 0 ) волны. Сразу за граничной частотой поле
очень далеко проникает в оболочку, и коэффициент фазы равен волновому
числу подложки. Далеко за граничной частотой поле полностью концентрируется в пленке, и коэффициент фазы приближается к волновому числу пленки.
Угол
наклона однородных плоских волн изменяется от граничного угла полного отражения при граничной частоте до нуля при очень высоких частотах. На
определенной частоте (например, соответствующей R= 3π) существует только
ограниченное число волн пленки (для R= 3π все волны вплоть до Н 2 и Е 2 ), углы
которых увеличиваются с возрастанием т.
До сих пор предполагалось, что материалы пленки и подложки полностью
однородны, поглощение в них отсутствует, а границы идеально плоские. В этом
случае волны пленки распространяются без затухания. На практике эти материалы вызывают потери, преимущественно из-за примесей и микроскопических
неоднородностей, рассеивающих свет. Кроме того, поскольку границы не совсем
плоские, то однородные плоские волны при полном отражении частично рассеиваются.
Затухание волн пленки можно представить суммой трех компонентов.
Первые два определяются поглощением и объемным рассеянием, причем они
131
лишь ненамного больше, чем для однородных плоских волн в таком же материале. Угол для всех волн пленки мал, особенно при малой разности показателей
преломления пленки и оболочки, поэтому путь элементарных волн по зигзагу
чуть длиннее, чем прямой путь.
Затухание воли пленки из-за излучения на нерегулярностях граничной поверхности зависит от параметров пленки. Чем тоньше пленка и чем
больше угол , тем чаще отражаются элементарные волны от граничных
поверхностей. Только волны низших порядков при достаточно толстой
пленке испытывают малое затухание за счет излучения на границе. Эта
компонента затухания сильно увеличивается с порядком волны.
Выбор и подготовка материалов пленки и подложки, метод нанесения
пленки должны обеспечивать получение однородной структуры с малыми
поглощением и рассеянием. Для пленок, работающих только в качестве
пассивных волноводов и не выполняющих никаких активных функций,
например усиления либо модуляции, нужно только малое затухание, обеспечиваемое выбором материала и конструкции. Такие пленки с малыми потерями изготавливают обычно из аморфных материалов, а именно стекла
или таких синтетических материалов, как полиуретан, полиэфирный эпоксид и органические полимеры. Малые потери имеют также аморфные
пленки из Та 2 O 5 . В качестве подложки, как правило, применяют стекло,
если интегральное устройство не требует другого материала. Пленки с малыми потерями из этих материалов толщиной от 1 до 10 мкм чаще всего
наносят электронно-лучевым распылением. Затухание пленки для волн
низших порядков в красном и инфракрасном диапазонах составляет около
1 дБ/см.
5.2 Оптические волокна и кабели
Волны ступенчатого оптического волокна состоят из исходного конечного числа волн сердцевины с дискретными значениями  nm  1c . Характеристические уравнения для Н т - или E т -волн при учете только меридиальных лучей получаются из (5.4) или (5.5) при подстановке п 0 = п 2 ; при этом
W = V. Для упрощения уравнения tg U выражают через tg (U/2) и приходят
к квадратному уравнению, решения которого для H-волн
tg(U/2) = V/U;
(5.10)
ctg(U/2) =-V/U;
(5.11)
и для E-волн
;
(5.12)
,
132
(5.13)
Уравнения (5.10) – (5.13) отражают симметрию пленки, приводящей к симметричным и антисимметричным относительно плоскости симметрии распределениям полей ее волн. Характеристическое ур-ние (5.10) соответствует H-волнам
с симметричным распределением поперечных полей, т. е. симметричным Н-волнам; другие уравнения описывают: (5.11) – антисимметричные Н-волны, (5.12)
– симметричные Е-волны и (5.13) – антисимметричные E-волны.
Уравнение (5.11) соответствует приближенной форме характеристического ур-ния (5.6) для всех волн в пленке толщиной d/2 на «мягкой» подложке
. Подставив указанную толщину пленки в формулу для параметра R,
можно с помощью рис. 5.3 и 5.4 определить поперечные постоянные фазы U,
затухания V и нормированный коэффициент фазы  для антисимметричной Нволны симметричной пленки. Это справедливо также для антисимметричной Еволны в слабонаправляющей симметричной пленке.
Характеристические ур-ния (5.10) и (5.12) для симметричных волн пленки
могут быть решены графически точно так же, как ур-ние (5.6) на рис. 5.3 для
пленки на «мягкой» подложке. На рис. 5.6 показано решение ур-ния (5.10); круг
радиуса R соответствует (5.7). Первая ветвь кривой начинается с нуля, так что
H0-волна ступенчатого световода, как и Е0-волна, существует при произвольно
малых значениях
, либо частоты. Следует отметить, что при малых значениях R поперечная постоянная затухания еще намного меньше, чем U, и протяженность поля снаружи чрезвычайно велика. Только когда R делается сравнимым с π/2, параметр V принимает значения, сопоставимые с U, и световод в действительности начинает направлять H0- и Е0-волны.
Рисунок 5.6 – Графическое решение
характеристического уравнения для симметричной H-волны в симметричной
пленке
Рисунок 5.7 – Нормированный коэффициент фазы для H-волн симметричной пленки; при слабонаправляющей симметричной пленке кривые справедливы
также для Em-волн того же порядка m
На рис. 5.7 показан в функции от R нормированный коэффициент фазы
всех Hm-волн, включая антисимметричные, вплоть до порядка m=4.
Для слабонаправляющих оптических волокон с
можно в ур-ниях
(5.12) и (5.13) принять отношение
. В этом случае рис. 5.7 справедлив для
133
Еm -волн. Все же при
для определенного R значения V и  для Hm -волны
всегда больше, чем соответствующей Еm -волны.
5.3 Распространение света и межмодовая дисперсия в градиентных
волокнах
Распространение света в градиентном волокне легко рассмотреть, однако
строгое рассмотрение приводит к значительным математическим трудностям.
Как видно из рис. 5.8, на котором изображено градиентное волокно, осевые лучи
проходят через волокно кратчайшим путем, но они преодолевают участок с
наибольшим значением показателя преломления, и следовательно, распространяются с наименьшей скоростью. Наклонные лучи, наоборот, проходят по более
длинным траекториям, однако большая часть их пути находится в среде с более
низким показателем преломления, в силу чего они распространяются быстрее.
Таким образом, можно представить себе, что при надлежащем выборе профиля
показателя преломления все лучи, сходящиеся в одну точку, могут быть сфокусированы вновь, образовав периодическую последовательность точек фокуса
вдоль волокна.
Траектория луча, распространяющегося в неоднородной среде (с изменяющимся показателем преломления), описывается выражением
d  dr 
 n   n
ds  ds 
.
(5.14)
где r – вектор положения точки на пути луча, ds – элементарное расстояние, измеряемое вдоль траектории.
Рисунок 5.8 – Градиентное волокно
Применим (5.14) к частному случаю цилиндрического волокна, в котором
показатель преломления радиально симметричен. Ограничимся рассмотрением
134
меридиональных лучей, и, кроме того, лишь тех из них, которые всегда остаются
почти параллельными оптической оси волокна. Это так называемое параксиальное лучевое приближение, которое позволяет нам аппроксимировать ds расстоянием вдоль оси dz. Тогда (5.14) принимает вид
d 2 r 1 dn

dz 2 n dr ,
(5.15)
где теперь r - расстояние луча от оптической оси, а z – расстояние, измеряемое вдоль оси. Легко показать, что параболический профиль показателя преломления обеспечивает синусоидальный закон изменения r от z. Пусть, например,


 n0 1  ' r / a 2 при r  a,
n( r )  
n0 (1  ' )  n(a) при r  a,
(5.16)
где п0 – показатель преломления на оси; а – радиус сердцевины волокна, а
'  n0  n(a)/ n0
(5.17)
полное относительное изменение показателя преломления сердцевины.
Дифференцирование (5.16) приводит к выражению
2n r
dn
  20 '
dr
a
.
(5.18)
Ограничившись в дальнейшем рассмотрением только лучей, расположенных близко к оси, можно предположить, что n0 / n1 ~ 1 . Тогда уравнение (5.15)
принимает вид
d 2r
2r
  2 '
2
dz
a
,
(5.19)
Если теперь рассмотреть лучи, которые вводятся в волокно таким образом,
что r  r0 , а dr / dz  r0 в точке z = 0, то интегрирование уравнения (5.19) даст следующее уравнение траектории луча:
r  r0 cos(2' )1 / 2
z
a
z
 r0'
sin(2' )1/ 2
1/ 2
a
a,
( 2 ' )
(5.20)
На рис. 5.9 приведены траектории двух групп таких лучей при r0 = 0 и r0' =
0. Все они не имеют дисперсии (не диспергируют).
Если попытаться ослабить условия параксиального приближения, то это
приведет к значительному усложнению уравнений. Можно, однако, показать,
что все меридиональные лучи не испытывают разбежки, если профиль показателя преломления имеет вид
135
5
 1

n(r )  n0 sch(r )  n0 1   2 r 2   4 r 4  ...
24
 2
.
(5.21)
Приведенное выше разложение профиля показателя преломления в ряд показывает, что параболический закон является первым приближением к требуе2
мому, если принять '  (a) / 2 . В случае косых лучей не существует такого закона изменения профиля показателя преломления, который бы устранил их взаимную дисперсию (независимо от места и угла ввода), а также дисперсию по отношению к меридиональным лучам.
Рисунок 5.9 – Траектории меридиональных лучей в волокне
с параболическим профилем показателя преломления:
Предполагается, что профиль показателя преломления имеет вид


n(r )  n0 1  ' (r / a) 2 , а все изображенные на рисунке траектории лучей заключены
в сердцевине. Имеется в виду, что траектории обладают круговой симметрией
относительно горизонтальных осей.
В заключении отметим, что для градиентных ОВ вводится понятие локальной числовой апертуры,
NA(r )  n12 (r )  n22 ,
которая показывает, что максимальный угол ввода оптического излучения
в этом случае определяется точкой сердцевины волокна, в которой находится
вершина конуса.
Числовая апертура характеризует лучи, которые захватываются ОВ,
однако, не все эти лучи будут распространяться, так как в ОВ распространяются
только лучи (моды) удовлетворяющие уравнению собственных волн ОВ Таким
136
образом, в волокне передается дискретный континуум лучей из их бесконечного
количества попавших в числовую апертуру.
5.4 Затухание в волноводах
Если рассматривать распространение света в установившемся состоянии,
то можно увидеть, что мощность P направляемого света уменьшается экспоненциально по мере увеличения длины L ОВ.
P( L)  P(0) 10

 L
10
,
(5.22)
где P(0) - мощность на входе ОВ,
 - киллометрическое (погонное) затухание (дБ/км).
Затухание за счет поглощения связано с потерями на диэлектрическую поляризацию, зависит от свойств материала и обратно пропорционально длине
волны
 п
где
n1
 tg  8,6 10 3

дБ/км,
(5.23)
n1  показатель преломления;
  длина волны;
tg  тангенс угла диэлектрических потерь.
Рассеяние обусловлено неоднородностями материала ВС, размеры которых меньше длины волны. Это рассеяние носит название релеевского
α р  K р /λ 4
,
(5.24)
где K р – коэффициент рассеяния и для кварца Кр=0,8...1,5 мкм4 дБ/км.
Собственное затухание определяется выражением
α α п α р
.
(5.25)
5.5 Дисперсионные искажения волоконно-оптического кабеля
В предельном идеализированном случае по волоконному световоду возможна организация огромного числа каналов на большие расстояния, но фактически имеются значительные ограничения. Это связано с тем, что сигнал на вход
приемного устройства приходит искаженным, и чем длиннее линия, тем более
искажается передаваемый сигнал. Данное явление носит название дисперсии.
Дисперсия – это рассеивание во времени спектральных или модовых составляющих оптического сигнала, которое приводит к увеличению длительности
импульса оптического излучения при распространении его по ОВ и определяется
137
разностью квадратов длительностей импульсов на выходе и входе ОВ Дисперсия
не только ограничивает частотный диапазон ОВ, но существенно снижает дальность передачи сигналов, так как чем длиннее линия, тем больше увеличивается
длительность импульсов.
Дисперсия в общем случае определяется четырьмя основными факторами:
различием скоростей распространения направляемых мод, направляющими
свойствами волокна, параметрами материала, из которого оно изготовлено и его
анизотропией. В связи с этим основными причинами возникновения дисперсии
являются, с одной стороны, большое число мод в ОВ (межмодовая дисперсия),
а с другой стороны – некогерентность источников излучения, реально работающих в спектре длин волн  (хроматическая дисперсия), анизотропия приводит
к возникновению поляризационной дисперсии. Межмодовая дисперсия преобладает в многомодовых ОВ и обусловлена отличием времени прохождения мод по
ОВ от его входа до выхода. Для ОВ со ступенчатым профилем показателя преломления скорость распространения электромагнитных волн с длиной волны 
одинакова и равна v  c / n1 , где c – скорость света. В этом случае все лучи, падающие на торец ОВ под углами к его оси в пределах 0     m , достигают приемного устройства с некоторым временным сдвигом, что, естественно, приводит к
увеличению длительности принимаемого импульса.
Межмодовая дисперсия градиентных ОВ, как правило, на порядок и более
ниже, чем у ступенчатых волокон. Это обусловлено тем, что за счет уменьшения
показателя преломления от оси ОВ к оболочке скорость распространения лучей
вдоль их траекторий изменяется – так, на траекториях, близких к оси, она
меньше, а удаленных – естественно, больше. Следовательно, лучи, распространяющиеся кратчайшими траекториями (ближе к оси), обладают меньшей скоростью, а лучи, распространяющиеся по более протяженным траекториям, имеют
большую скорость. В результате время распространения лучей выравнивается и
увеличение длительности импульса становится меньше. Так как межмодовая
дисперсия не зависит от характеристик источника излучения, для многомодовых
волокон ее оценивают по полосе пропускания ОВ ( МГц  км ).
Отличие времени распространения каждой из направляемых мод, образующих сигнал, от частоты спектра источника оптического излучения приводит к
возникновению так называемой хроматической дисперсии, которая, в свою очередь, складывается из волноводной дисперсии и материальной дисперсии.
Первый тип дисперсии обусловлен направляющими свойствами сердцевины ОВ, а именно зависимостью групповой скорости моды от длины волны оптического излучения, что приводит к различию скоростей распространения частотных составляющих излучаемого спектра. Поэтому волноводная дисперсия в
первую очередь определяется профилем показателя преломления ОВ и пропорциональна ширине спектра излучения источника  , т.е.
 в    L  M 1 ( ) ,
138
(5.26)
где M 1 ( ) – коэффициент волноводной дисперсии (пс/нм  км).
Второй тип дисперсии вызван зависимостью показателя преломления
сердцевины от длины волны n1 ( ) , что, как и в предыдущем случае, приводит к
различным скоростям распространения спектральных составляющих источника
излучения. Возникающая при этом различная задержка частотных составляющих распространяющегося в ОВ излучения определяет дисперсию материала,
которая равна
 мат    L  M 0 ( ) ,
(5.27)
где M 0 ( ) – коэффициент материальной дисперсии (пс/нм  км).
Здесь следует отметить, что материальная дисперсия кварцевого ОВ при
определенной частоте имеет нулевое значение, так как при длине волны  =1,28
мкм она изменяет свой знак. Эта точка носит название точки нулевой материальной дисперсии. Очевидно, что, изменяя соотношение между волноводной и материальной дисперсией, точку нулевой дисперсии можно перемещать в небольших пределах, что используется в волокнах со смещённой дисперсией, в которых
нуль хроматической дисперсии сдвинут в область третьего окна прозрачности,
где затухание минимально.
Анизотропия, возникающая в ОВ вследствие неидеальности их геометрии
и механических нагрузок приводит к появлению эффекта двулучепреломления.
Поэтому монохроматический свет с данным состоянием поляризации делится
ОВ на две световые волны с ортогональными поляризациями, распространяющиеся с различными скоростями.
Для оценки дисперсии, возникающей вследствие задержки распространения ортогонально поляризованных световых волн, используется понятие поляризационной модовой дисперсии:
   k L ,
(5.28)
где k – коэффициент удельной поляризационной дисперсии, который нормируется в расчете на 1 км и имеет размерность nc / км .
Поляризационная модовая дисперсия проявляется исключительно в одномодовых волокнах с нециркулярной (эллиптической) сердцевиной и при определенных условиях становится соизмеримой с хроматической дисперсией. Поэтому результирующая дисперсия одномодового волокна должна определяться в
соответствии с выражением
   мм 2  ( в   мат ) 2    2
.
(5.29)
Дисперсия приводит к уменьшению пропускной способности ОВ или к сокращению длины оптического тракта между пунктами восстановления параметров оптического сигнала.
139
5.6 Затухание в основных элементах волоконно-оптического тракта
Основными элементами оптического тракта являются: устройства ввода
оптического сигнала от источников излучения, разъемные и неразъемные соединения, устройства согласования ВС и приемного оптического модуля.
В последние годы в современных ВОСП широко используются различного
типа ответвители, оптические фильтры и т.д. Студент должен изучить принцип
работы этих устройств и уметь определить затухание и их другие характеристики.
Затухание в соединениях определяется следующим выражением:
 l  Ф   а   Na   d   D   И   q
где
a
 Na
d
D
И
.
(5.30)
 Ф - затухание из-за френелевского отражения;
- затухание из-за различия радиусов соединяемых ВС;
- затухание из-за различия в значениях числовых апертур;
- затухание из-за несоосности соединяемых ОВ;
- затухание из-за зазора между 0В;
- затухание из-за углового смещения;
 q - затухание из-за различного профиля волокна.
Соединение может быть разъемным и неразъемным (сварным).
Неразъемные оптические соединения обеспечивают минимальный уровень оптических потерь в пределах 0,1.... 0,5 дБ в зависимости от типа волокна и технологии изготовления соединения. В этом случае затухание вследствие френелевского отражения и из-за зазора между волокнами равно нулю.
Затухание из-за зазора между соединяемыми волокнами за малостью
можно не учитывать также и в разъемных соединениях. Затухание за счет френелевского рассеяния
2

 n1  n0  
 
 Ф  10 lg 1  2

 n1  n0  
,
(5.31)
где n1 , n0 - показатели преломления сердцевины ВС и заполнения между
торцами соединяемых волокон.
В зависимости от типа волоконного световода потери на соединениях
определяются различными выражениями. Для многомодовых волокон затухания, определяемые разными факторами, равны соответственно
140
 a  10lgа 1/а 2 2 , при a 1  a 2 ;
(5.32)
 Na  10 lg NA1(O)/NA2(O)2 , при NA1(O)  NA2(O) .
(5.33)

 q  10lg q1 /q 2

q1  2 

q2  2  , для q2  q1 ;
(5.34)
2
d

 d  10lg1  0,64 
a  , для ступенчатого ВС;

(5.35)
2
d

 d  10lg1  0,85 
a  , для градиентного ВС;


 И  10 lg 1 


n1n0
(5.36)


2  ,
(5.37)
где n1 - показатель преломления сердцевины;
n0 - показатель преломления среды между соединяемыми волокнами;
а - радиус ВС;
d - осевое смещение.
Распределение поля на торце одномодового световода может быть с хорошей точностью аппроксимировано гауссовой функцией


E (2)  A exp  r 2 / w02 , при 0  r  a ,
(5.38)
где w0 - полуширина на уровне, где напряженность поля равна 1/е.
Поэтому затухание определяется следующими формулами:
2
 2w  w 
 w  10lg 201 022 
 w01  w02  ,
(5.39)
 d  10lgexp - d 2 / w02  ,
(5.40)
   n2  w0   




2
 И  10lgexp - 
где
 - длина волны;
(5.41)
w01, w02 - полуширины соединяемых волокон.
Затухание при возбуждении ВС от источника излучения
1
2
 И-ВС  10lg NA 2 (G  1)
(5.42)
где G – параметр, характеризующий направленность излучения проводникового лазера (G=l для светодиодов);
NA - числовая апертура 0 В.
141
6 ПАССИВНЫЕ КОМПОНЕНТЫ ВОЛОКОННО-ОПТИЧЕСКИХ
СИСТЕМ ПЕРЕДАЧИ
6.1 Пассивные оптические элементы
Цель этой главы – описать различные пассивные устройства, используемые в волоконно-оптических сетях. Существует пять основных типов волоконно-оптических сетей:
1 Глобальные сети (с большой длиной пролета) общего или частного пользования.
2 Офисные сети и сети масштаба предприятия, называемые также внутриобъектными сетями.
3 Местные распределительные сети, включающие сети кабельного телевидения (КТВ), в частности, сети, использующие гибридные (с медными и оптическими жилами) кабели.
4 Региональные сети (класса «Метро», MAN), осуществляющие передачу
данных аналогично тому, как это делается в сетях масштаба предприятия: сети
либо доставляют данные локально, либо передают потоки данных по всему региону.
5 Сети специального назначения, обычно передающие сигнал на очень короткие расстояния.
Каждый тип сети требует использования определенного числа как общих,
так и специальных типов пассивных устройств. Например, кабельные телевизионные сети широко используют разветвители.
WDM/DWDM сети используют широкую номенклатуру специальных пассивных устройств. Мы опишем их в соответствующей главе о WDM.
В этой главе мы в первую очередь опишем волоконно-оптические соединители (оптические разъемы) и неразъемные соединения (сростки). Также будут
рассмотрены следующие пассивные устройства:
 оптические разветвители, расщепители сигнала (сплиттеры), элементы
разветвления потока;
 оптические изоляторы;
 волоконно-оптические фильтры;
 оптические аттенюаторы;
 оптические (пассивные) коммутаторы;
 пассивные компенсаторы (хроматической) дисперсии;
 оконечные (терминирующие) элементы.
Каждое устройство, используемое в схеме передачи светового сигнала, является источником вносимых потерь. Оно также будет источником отражений,
обычно характеризуемых потерями на отражение. Эти потери обычно измеряются в децибелах. За исключением аттенюаторов, хотелось бы иметь как можно
более низкие вносимые потери и как можно более высокие потери на отражение
142
(возвратные потери). Например, хочется иметь сростки с уровнем вносимых потерь меньше, чем 0,1 дБ, но с уровнем возвратных потерь больше, чем 40 дБ.
6.2 Основные определения
6.6.1. Элемент, ответвляющий поток (неселективный по отношению к
длине волны)
Ответвителем является неселективный пассивный элемент, обладающий
тремя или более портами и распределяющий мощность между ними в определенном соотношении без какого-либо усиления, переключения или какой-то модуляции.
6.6.6. Оптический разветвитель (сплиттер – комбайнер)
Термин разветвитель используется как синоним элемента ответвляющего
поток. Он используется также для определения структуры, распределяющей оптическую мощность между двумя оптическими волокнами или между активным
устройством и волокном.
6.6.3. Аттенюатор
Аттенюатор – пассивный элемент, осуществляющий управляемое ослабление сигнала в волоконно-оптической линии передачи (ВОЛП).
6.6.4. Волоконно-оптический фильтр
Фильтр – пассивный элемент, используемый для модификации проходящего через него оптического излучения, как правило, за счет изменения спектрального распределения мощности. В частности, волоконно-оптические фильтры обычно используют для отсечения или поглощения оптического излучения
в определенных областях длин волн и пропускания излучения на других длинах
волн.
6.6.5. Волоконно-оптический изолятор
Изолятор – оптическое устройство, не обладающее свойством взаимности, предназначенное для подавления обратного отражения в ВОЛП и имеющее минимальные
вносимые потери в прямом направлении.
6.6.6. Волоконно-оптический терминатор
Терминатор (оконечный элемент) – элемент, используемый для терминирования
оптоволокна (оконцованного или нет) с целью подавления отражения.
6.6.7. Волоконно-оптический переключатель (коммутатор)
Переключатель (коммутатор) – пассивный элемент, имеющий один или больше
портов, которые передают, блокируют или перенаправляют оптическую мощность в
одно из волокон ВОЛП.
6.6.8. Пассивный компенсатор (хроматической) дисперсии
Компенсатор – пассивный элемент, используемый для компенсации хроматической дисперсии одного из оптических трактов.
6.6.9. Волоконно-оптический соединитель(оптический разъем)
143
Оптический разъем – элемент, прикрепленный к одному из оптических кабелей
или отдельной части оборудования для осуществления частых соединений/разъединений оптических волокон или кабелей.
6.6.10. Сращивание оптических волокон
Сращивание – постоянное (неразъемное) или полупостоянное (разбираемое, с
технологическим зазором) соединение между двумя оптическими волокнами, осуществляемое для объединения их оптических потоков. Различают:
 сварное соединение: сращивание, при котором концы волокна соединяются
в постоянное непрерывное соединение с помощью сварки;
 механическое соединение: сращивание, при котором концы волокна соединяются в постоянное соединение без помощи сварки.
6.3 Определение функциональных параметров
6.3.1. Вносимые потери (IL)
Вносимые потери – уменьшение оптической мощности между входным и
выходным портами пассивного элемента в дБ, определяемое как
IL  10 log( P1 / P0 ),
(6.1)
где P0 – оптическая мощность, вводимая во входной порт, а P1 , – оптическая мощность, полученная из выходного порта.
Замечание 1. Для волоконно-оптического элемента ветвления они соответствуют элементу
a ij
(где i  j ) логарифмической матрицы передачи.
a ij
Замечание 6. Для устройства WDM они соответствуют элементу
(где
i  j ) логарифмической матрицы передачи и должны быть определены для каждой рабочей длины волны.
Замечание 3. Для волоконно-оптического переключателя (коммутатора)
a ij
они соответствуют элементу (где i  j ) логарифмической матрицы передачи и
зависят от состояния переключателя (коммутатора).
Замечание 4. Для волоконно-оптического фильтра они должны быть определены для каждого рабочего диапазона длин волн.
Вносимые потери являются отношением оптической мощности, подаваемой на входной порт соответствующего оптического устройства, к оптической
мощности, излучаемой из любого выходного порта, выраженной в дБ. Вносимые
потери включают такие параметры, как потери на разветвление, в случае разветвителей, для других устройств ветвления мы используем понятие дополнительные потери. Эти потери являются наиболее полезными параметрами при проектировании систем. Максимальные и минимальные вносимые потери являются
144
соответственно верхним и нижним пределами вносимых потерь рассматриваемого устройства и применяются во всем диапазоне длин волн, определенном для
данного фильтра. Под типичными вносимыми потерями понимается ожидаемое
значение вносимых потерь, измеренное для определенной центральной длины
волны. Институт IEEE определяет вносимые потери, как «полные потери оптической мощности, вызванные внесением/наличием такого оптического элемента,
как оптический разъем, сросток или разветвитель».
6.3.6. Возвратные потери (RL)
Возвратные потери – часть входной мощности, которая возвращается из
входного порта пассивного элемента. Они определяются, как
RL  10 log( Pr / Pi ) ,
(6.2)
где Pi – оптическая мощность, вводимая во входной порт, а Pr – оптическая
мощность, полученная обратно из того же порта.
Замечание. Для определенности, величина возвратных потерь для волоконно-оптических устройств не учитывает вклад от возвратных потерь оптических разъемов, этот вклад рассматривается отдельно.
6.3.3. Отражательная способность
Отражательная способность – отношение R отраженной мощности Pr к падающей мощности Pi , определенное для данного порта пассивного элемента при
заданных условиях спектрального распределения, поляризации и геометрического распределения, выраженное в дБ, а именно:
R  10 log( Pr / Pi ).
(6.3)
При рассмотрении мощности, отраженной от отдельного элемента, отражательная способность является более предпочтительным параметром по сравнению с возвратными потерями. Для определенности, величина отражательной
способности волоконно-оптического устройства не включает вклад отражательной способности оптических разъемов, этот вклад рассматривается отдельно.
6.3.4. Предварительное
обсуждение
направленности,
возвратных потерь и отражательной способности
Направленность – отношение оптической мощности, вводимой во входной
порт, к оптической мощности, возвращаемой от любого другого порта. Направленность рассматривается как характеристика изоляции, или перекрестной помехи, на ближнем конце. Возвратные потери являются отношением оптической
мощности, вводимой во входной порт, к оптической мощности, которая возвращается из того же порта. Как направленность, так и возвратные потери, выражаются в дБ (они рассматриваются как положительные значения) и измеряются при
условии оптического терминирования всех других портов. Отражательная спо-
145
собность фактически является возвратными потерями, взятыми с обратным знаком. Во многих случаях эти два понятия используются как синонимы. Минимальные направленность и возвратные потери являются теми нижними пределами, которые применяются во всем диапазоне длин волн, определенном для полосового фильтра.
6.3.5. Рабочий диапазон длин волн
Это диапазон длин волн от i min до r max в пределах, задаваемых от номинального  j , внутри которого пассивные элементы должны работать с определенными показателями ошибок.
Замечание 1. Для волоконно-оптических элементов ветвления, использующих
более одного рабочего диапазона длин волн, соответствующие диапазоны длин волн
не обязательно одинаковы.
Замечание 6. Элементы, такие как аттенюаторы, терминаторы, оптические
разъемы и сростки, могут работать с определенными (или приемлемыми) показателями ошибок даже за пределами определенной для них области применения.
6.3.6. Потери, зависящие от поляризации (PDL)
Эти потери соответствуют максимальной вариации вносимых потерь, вызванной вариацией состояния поляризации, рассматриваемой на множестве всех возможных состояний поляризации.
6.3.7. Зависимость отражательной способности от поляризации
Эти потери соответствуют максимальной вариации отражательной способности, вызванной вариацией состояния поляризации, рассматриваемой на множестве
всех возможных состояний поляризации.
6.3.8. Обратные потери (степень изоляции) волоконно-оптических изоляторов
Обратные потери – мера уменьшения оптической мощности (в дБ), распространяющейся в обратном направлении, в результате установки изолятора. Излучающим портом здесь является выходной порт изолятора, а приемным портом – входной порт изолятора. Потери определяются следующей формулой:
BL  10 log( Pob / Pib ),
(6.4)
где Pob - оптическая мощность, измеренная на входном порте изолятора, когда
мощность Pib излучается в рабочий порт. При нормальной работе Pib – оптическая мощность, отраженная от устройств, установленных на удаленном конце оптической линии, и направленная обратно так, что попадает в выходной порт изолятора, потери
которого и измеряются.
6.3.9. Направленность
Для волоконно-оптических элементов ветвления, направленность представлена
значением а – элемента логарифмической матрицы передачи между двумя изолированными портами.
6.3.10.
Однородность
146
Логарифмическая матрица передачи элементов ветвления может содержать
определенный набор коэффициентов, который конечен и одинаков. В этом случае
диапазон изменения этих коэффициентов aij (выраженный в дБ) именуется однородностью элементов ветвления.
6.3.11.
Оптический порт
Портом является вход оптического волокна или оптического разъема (присоединенного к оптическому элементу), используемый для ввода оптической мощности.
6.3.16.
Матрица
передачи
волоконно-оптических
устройств
ветвления и WDM-устройств
Оптические свойства волоконно-оптических устройств ветвления могут быть
определены в терминах матрицы коэффициентов п х п, где п - число портов, а коэффициенты представляют часть мощности, передаваемой между назначенными портами. В общем случае матрица передачи T имеет вид:
где t ij – отношение оптической мощности Pij , передаваемой из порта j, к оптической мощности Pi , подаваемой на порт i. То есть,
t ij  Pij / Pi .
Замечание. В общем случае t ij может зависеть от длины волны.
6.3.13.
Коэффициент передачи волоконно-оптических устройств ветвления и WDM-устройств
Коэффициентом передачи является элемент t ij матрицы передачи.
6.3.14.
Логарифмический коэффициент матрицы передачи волоконно-оптических устройств ветвления и WDM-устройств
В общем случае логарифмическая матрица передачи имеет вид
где aij – коэффициент уменьшения оптической мощности (в дБ), выходящей
из порта j, при единичной мощности, приложенной к порту i, то есть,
aij  10 log( t ij ),
147
где t ij – коэффициент матрицы передачи.
6.3.15.
Матрица передачи волоконно-оптических коммутаторов
Оптические свойства волоконно-оптического коммутатора могут быть определены матрицей коэффициентов т х п (где п – число портов). Матрица Т отображает
пути передачи в состоянии включено (передача в расчете на худший случай), а матрица T o – пути передачи в состоянии выключено (изоляция в расчете на худший случай).
6.3.16.
Коэффициенты передачи волоконно-оптических коммутаторов
Коэффициентом передачи является элемент t ij или t
o
ij
матрицы передачи. Каж-
дый коэффициент t ij определяет минимальную (в расчете на худший случай) часть
мощности, переданную от порта i к порту j, для любого состояния, при условии,
o
что путь ij включен. Каждый коэффициент t ij определяет максимальную (в расчете
на худший случай) часть мощности, переданную от порта i к порту j, для любого состояния, при условии, что путь ij выключен.
6.3.17.
Логарифмическая матрица передачи волоконно-оптических коммутаторов
В общем случае логарифмическая матрица передачи имеет вид:
где aij – коэффициент уменьшения оптической мощности (в дБ), выходящей
из порта j, при единичной мощности, приложенной к порту i, то есть,
aij  10 log( t ij ),
148
где t ij – коэффициент матрицы передачи.
Аналогично, для состояния выключено, имеем a ij  10 log( t ij ),
6.3. 18. Избыточные потери волоконно-оптических устройств ветвления
Избыточные потери – это общая мощность, потерянная в устройствах ветвления,
когда оптический сигнал подается в порт i. Они определяются как
0
0
ELi  10 log  j t ij ,
где суммирование осуществляется только по тем значениям j, для которых i и j
– проводящие порты. Для устройства ветвления с N входными портами будет существовать массив из N значений избыточных потерь, по одному значению для каждого входного порта i.
6.3.19.
Коэффициент связи
Для заданного входного порта i коэффициент связи является отношением светового потока на заданном выходном порту k к общему световому потоку со всех выходных портов. Он определяется так:
CRik  t ik /  j t ij ,
где индексом j обозначены все функционирующие выходные порты.
6.3.20.
Рабочая длина волны
Это номинальная длина волны  , на которой пассивный элемент должен (по
проекту) работать с надлежащими показателями.
6.3.21.
Матрица времен переключений волоконно-оптического коммутатора
Матрица S является матрицей таких коэффициентов, что каждый элемент S ij
характеризует максимальное время переключения, требуемое для того, чтобы пере-
вести путь ij из любого состояния в состояние включено или выключено.
6.4 Разъемные и неразъемные соединения
Оптические разъемы и неразъемное соединение (сращивание) волокон используются для соединения секций волокна (кабеля). Волоконно-оптический кабель (ВОК) доставляется производителю работ на катушках с намотанным кабе-
149
лем длиной 1-25 км. Для систем дальней связи, в отличие от сетей в офисе клиента, катушки состоят из сегментов кабеля (строительных длин), которые
должны быть соединены вместе для создания рабочей системы. Для этой цели
используются либо оптические разъемы, либо сращивание волокон.
Промышленная практика диктует (в хорошем смысле) использование оптических разъемов на обоих концах кабеля и сращивание для промежуточных
секций. Причины такой практики в следующем:
 Сростки дают вносимые потери минимально на уровне 0,04 дБ на один
сросток, тогда как оптические разъемы имеют большие вносимые потери. Кроме
того, сростки обеспечивают определенное постоянство.
 Это вынуждает использовать оптические разъемы в тех местах, где мы
ожидаем несколько или много соединений/разъединений, например, в коммутационных панелях или соединительных кроссах. Многие оптические разъемы сделаны для осуществления легкого сочленения (соединения/разъединения).
Возможность использования оптических разъемов должно рассматриваться там, где волокно стыкуется либо с пассивным, либо с активным устройством. Если мы хотим заменить устройство, то это значительно удобнее сделать
при наличии оптического разъема, чем сростка.
6.4.1. Оптические разъемы
На рынке существует большое количество специализированных оптических разъемов. Волоконно-оптические разъемы доступны в двух типоразмерах:
разъемы стандартного размера и миниатюрные оптические разъемы. Существуют оптические разъемы, которые могут соединить как одно, так и несколько
волокон.
Одни оптические разъемы могут быть спроектированы для соединений в полевых условиях, другие – для соединения в заводских условиях. К последним типам относятся оптические разъемы для соединительных шнуров (пигтейлов). Соединительный шнур – короткий по размеру одноволоконный кабель, присоединяемый обычно
к устройствам типа: источник света или детектор светового сигнала. Другой конец
такого шнура имеет оптический разъем, устанавливаемый производителем устройства. Если соединение производят в полевых условиях, необходимо предусмотреть ответную часть для такого типа разъема, установив ее на конце соединяемого волокна.
Оставшаяся часть материала главы будет сконцентрирована только на оптических разъемах, устанавливаемых в полевых условиях.
6.4.6..1. Конструкция оптических разъемов – общий случай
Оптический разъем состоит из трех основных частей:
1. Наконечник – ферул.
2. Соединительная розетка.
3. Стягивающая гайка.
Вид типичного оптического разъема в сборке приведен на рис. 6.1.
150
Соединительная
розетка
Наконечник
(ферул)
Оптическое
волокно
Стягивающая
гайка
Оптический кабель
Мультипорт
Адаптер
Пластиковый
многоволоконный
наконечник (ферул)
Рисунок 6.1 – Основная структура оптического разъема(ов)
Обычно оптический разъем состоит из оболочки, внутри которой расположен
керамический наконечник (ферул) с прецизионным продольным концентрическим
каналом. Оголенный отрезок волокна вставляется в канал наконечника и удерживается резиной или термоплавким клеем. Выступающий конец волокна затем скалывается и полируется заподлицо (плоское зеркальное полирование). Металлическая оболочка выравнивается и соединяется встык с керамическим наконечником мягкой
опрессовкой. Наиболее распространенный внешний диаметр наконечника - 2,5 мм,
но в оптических разъемах с малым форм-фактором может использоваться наконечник
диаметром 1,25 мм.
Для одномодового волокна точность выравнивания лучше, чем 0,1 мкм, а допуск на угловое выравнивание составляет 5°. Обычно рекомендуется контролировать
вносимые потери установленного оптического разъема перед тем, как отправить его
151
потребителю. Эти потери должны быть измерены по стандартной технологии измерений, а не с помощью оптического временного рефлектометра (OTDR). Возможно
при этом потребуется проконтролировать возвратные потери с учетом интерфейса
оптического разъема. Это можно сделать с помощью OTDR. Цель последних измерений – убедиться, что возвратные потери имеют порядок 40 дБ или лучше.
На рынке существует большое разнообразие типов оптических разъемов, каждый из них требует своей собственной процедуры сборки. Однако, по крайней мере,
два шага этой процедуры являются общими для них всех.
Рисунок 6.2 – Применение эпоксидной смолы
Во-первых, волокно закрепляется в оптическом разъеме с помощью эпоксидной смолы. Этот процесс важен с точки зрения обеспечения надежности оптического
разъема. Эпоксидная смола минимизирует температурные перемещения волокна,
позволяя осуществлять полировку торца без боязни повредить волокно, кроме того
она предохраняет волокно от воздействия окружающей среды. И, наконец, она допускает очистку торцов от клея на последней стадии. Поэтому очень важно, чтобы
эпоксидная смола присутствовала на всей длине отрезка голого волокна, вокруг буфера (там, где волокно входит в оптический разъем), а также вокруг кончика волокна, выступающего из наконечника (см. рис. 6.2).
Во-вторых, оптоволоконный торец на конце оптического разъема должен
быть отполирован. Рекомендуется полирование типа физический контакт (PC). Это
означает, что концы волокон будут физически соприкасаться внутри адаптера оптического разъема, как если бы они находились под давлением. Отсутствие полировки
типа PC приводит к образованию воздушного зазора между волокнами и увеличению затухания. Описанное, показано на рис. 6.3.
Существует несколько рекомендованных методов полирования, которые, как
правило, зависят от материала наконечника. В общем случае, если материал наконечника очень твердый, например керамика, то, как правило, наконечник закруглен в
районе торцевого конца и на него ссылаются как на предварительно закругленный.
Мягкие материалы наконечника, такие, как композитные термопластики или стеклокерамика, могут полироваться плоско. Эти материалы изнашиваются примерно с такой же скоростью, что и оптоволокно, могут интенсивно полироваться и, тем не менее, поддерживать качество физического контакта.
152
Рисунок 6.3 – Иллюстрация физического контакта (PC)
в волоконно-оптическом разъеме
Существуют несколько подходов в процессе подготовки волокна и оптического разъема к сборке. Торцевые концы волокна, которые оконцовываются
оптическими разъемами, в настоящее время закругляются, вместо того, чтобы
делать их плоскими и перпендикулярными. Преимущество такого подхода в том,
что свет не отражается непосредственно назад к источнику (так как угол отражения равен углу падения). Теперь он отражается назад под углом и, как правило,
оказывается потерянным для волокна. Радиальная полировка сначала отсекает
часть отраженного света, а затем направляет то, что отразилось, так, что оно никогда не достигает исходного источника излучения. Этот подход называется полировкой торца до уровня физического контакта. Другое преимущество подхода,
использующего полировку закругленного конца до уровня физического контакта, в том, что волокна касаются наиболее выступающими точками, которые
приходятся на среднюю часть светонесущей сердцевины. Пользователь убежден,
что волокна касаются всегда и что воздушный зазор исключен.
Обратное отражение может быть снижено еще больше, если использовать
угловой физический контакт (АРС). Угловой контакт отражает свет в оболочку
волокна, а не в сердцевину.
Возвратные потери оптического разъема должны быть, по крайней мере,
40 дБ. Другой важный параметр – число сочленений. Оно относится к числу соединений/разъединений, начиная с которого характеристики разъема станут
ухудшаться. Это число, как показывает опыт, колеблется от 200 до 600 сочленений.
6.4.1.6. Типы оптических разъемов
Оптический разъем типа ST. Этот тип разъема использует быстро сочленяемое байонетное соединение, которое требует повернуть разъем только на четверть оборота для осуществления соединения/разъединения. Встроенный ключ
обеспечивает хорошую повторяемость параметров соединения, потому что
разъем будет всегда одинаково сочленен с соединительной втулкой. Разъем типа
ST в настоящее время заменяется на более прогрессивный разъем типа SC. Уровень вносимых потерь разъема типа ST составляет 0,5 дБ.
Оптический разъем типа SC. Этот тип разъема широко используется как
для одномодового, так и для многомодового волокна. Сокращение SC расшифровывается как «оптический разъем пользователя». Оно пришло из используемых ранее пользовательских приложений.
153
Разъем SC относится к классу разъемов общего пользования и применяется
как в сетях с большой длиной секций, так и в сетях с внутриобъектовой прокладкой. Он использует «пушпульный» механизм сочленения. Разъем SC базового
типа состоит из сборки (вилки), содержащей наконечник. Эта сборка вставляется
в оболочку разъема, центрирующую наконечник. Одно из преимуществ разъема
типа SC в том, что он может объединяться в секцию, состоящую из нескольких
разъемов. В этом случае секция может использоваться для дуплексного соединения (одно волокно которого используется для передачи в прямом, а другое в обратном направлениях). Разъем имеет ключ, для предотвращения неправильного
соединения. Вносимые потери такого разъема составляют 0,4 дБ и ниже.
Оптический разъем типа FC. Этот тип разъема был первоначально разработан в Японии компанией Nippon Telegraph and Telephone Company. Он широко
используется для одномодового волокна и имеет уровень вносимых потерь порядка 0,4 дБ.
Разъем типа FC имеет средства для настройки. Ключ настройки позволяет
подстроить уровень вносимых потерь до нескольких десятых дБ. После того, как
позиция минимальных потерь найдена, ключ может быть зафиксирован. Разъем
типа FC выпускается как для одномодового, так и для многомодового волокон.
Оптический разъем типа D4. Этот тип разъема особенно широко используется для одномодового волокна. Он во многих отношениях похож на разъем FC,
но имеет наконечник меньшего диаметра – 2,0 мм. Вносимые потери разъема D4
составляют около 0,4 дБ.
Оптический разъем типа 568SC. Этот тип разъема обычно используется для
внутриобъектовой прокладки. Его параметры соответствуют стандарту EIA/TIA568, регламентирующему прокладку кабельных линий связи в коммерческих зданиях. По сути он представляет собой дуплексный вариант разъема типа SC.
Разъем типа 568SC имеет механизм защелки, который позволяет осуществить
сочленение легче, чем байонетный разъем типа SC. Кроме того, этот разъем
имеет адаптер, который допускает использование как симплексного, так и дуплексного разъемов для организации симплексного или дуплексного соединений.
Ожидаемый уровень вносимых потерь разъема 568SC составляет порядка 0,3 дБ.
Оптический разъем типа FDDI. Этот тип разъема в принципе спроектирован как двухканальное устройство, использует два керамических наконечника и
механизм боковых защелок. Прочный кожух защищает наконечники от случайных повреждений, тогда как плавающий стык обеспечивает ему плотное сочленение без усилий. Различные типы ключей могут быть использованы в этом типе
разъема, для того чтобы удовлетворить различным требованиям технологии
FDDI. Ожидаемый уровень вносимых потерь составляет порядка 0,3 дБ для одномодовых приложений и порядка 0,5 дБ для многомодовых приложений. Разъемы типа FDDI могут использоваться и для других приложений. Напомним, что
FDDI - технология локальных сетей, используемая для пакетной передачи данных со скоростью 100 Мбит/с (125 Мбод) в соответствии со стандартом ANSI.
Миниатюрные разъемы. Миниатюрные разъемы, называемые также разъемами с малым форм-фактором, имеют размеры примерно в два раза меньшие,
154
чем их обычные стандартные варианты (например, SC, FC, ST), т.е. диаметр
наконечника составляет 1,25 мм, а не 2,5 мм, что позволяет реализовать большую
плотность упаковки на коммутационной панели и плотную схему упаковки на
стойке. В табл. 3.1 приведены основные параметры четырех наиболее известных
миниатюрных разъемов.
Таблица 6.1 – Сравнение параметров миниатюрных разъемов четырех типов.
Расстояние
между волокнами, мм
Число стержней
Материал
стержня
Выравнивание
6,25
0,75
0,75
4,5
2
керамика
1
пластмасса
1
пластмасса
0
отверстие и
наконечник
Ø1,25
направляющая и
наконечник
Ø 2,5
V-образная
канавка
Размер стержня,
мм
Трансивер, проход
ширина, мм
длина, мм
Тип кабеля
центровочный штырь и
наконечник
2,5 х 4,4
11,1 мм
7,2 мм
11 мм
12,1 мм
5,7
14,6
дуплексный
5,7
14
дуплексный/
ленточный
7,5
12,7
дуплексный/
ленточный
8
21
GGP,
покрытый
полимером
Область вилки
заливка и
полировка
предвари
тельно
полированный выступ
вилка+разветвитель и
розетка
типа RJ – на
верху
предварительно
полированный выступ
Вилка+разветвитель
–
Область розетки вилка+разветвитель
Защелка
2 типа RJ,
связанные
сверху
типа SC –
пушпульные
–
–
скол и
полирован
ная розетка
типа RJ наверху
Замечание. Вносимые потери этих оптических разъемов изменяются в диапазоне от 0,3 до 0,6 дБ.
6.4.6. Неразъемное соединение волокон
Неразъемное соединение, или сросток, постоянно соединяет два волокна.
Существуют два типа соединений (сростков):
1. Механическое соединение.
2. Сварное соединение.
155
Самое важное в процедуре формирования неразъемного соединения (или
сращивания) – точно выровнять концы двух волокон перед их соединением. Хорошая полировка концов волокон и их очистка также важны при совершении
этой процедуры.
6.4.6.1.
Механическое соединение
Механическое соединение – небольшой участок механически соединенного оптоволокна – сросток длиной 6 см и диаметром 1 см. Этот сросток осуществлен путем точного выравнивания двух концов волокон и их надежного постоянного механического соединения. Сросток закреплен с помощью быстросхватывающего покрытия или клеевой обвязки, или с использованием того и другого.
Механические сростки допустимы как для организации постоянного, так и временного соединения. Вносимые потери за счет механического соединения
обычно выше, чем сварного соединения, и имеют порядок 0,1 – 0,8 дБ.
Одномодовое волокно, учитывая небольшой размер его сердечника и, следовательно, малый диаметр поля моды, более чувствительно к ошибкам выравнивания волокна в месте сращивания. Следовательно, устройства механического
сращивания, способные обеспечить достижение приемлемых вносимых потерь в
бюджет потерь одномодового волокна, стоят дороже, требуют больше времени
для сращивания и могут потребовать затрат на капиталовложения, сравнимых с
теми, что используются для сварки.
6.4.6.6.
Соединение с помощью сварки
Сварное соединение наиболее широко используется для постоянного соединения одномодового волокна. Получение хорошего сварного сростка значительно проще сейчас, учитывая постоянный прогресс сварочного оборудования,
процедур и практики сварки, в дополнение к постоянному улучшению контроля
за геометрией волокна в процессе производства. В результате, типичный диапазон достигаемых вносимых потерь составляет 0,04 – 0,1 дБ как для одномодовых,
так и многомодовых волокон.
Качество сварного соединения. Два параметра влияют на качество сварного
соединения: вносимые потери сростка и прочность на растяжение.
Для многомодового волокна, существуют факторы, зависящие от самого
волокна, они включают несовпадение диаметров волокон, несовпадение числовых апертур, несовпадение показателей преломления и ошибки концентричности сердцевины и оболочки. Концентричность показывает, насколько точно круг
сердцевины вписывается в кольцо окружающей ее оболочки, т.е. какова величина смещения центров обоих окружностей. Этот тип потерь может быть уменьшен путем использования техники сращивания, дающей возможность выровнять
положение сердцевины волокон в месте соединения. Из рис. 6.4 можно оценить
основные теоретические потери на сращивание, вызванные их основными причинами: несовпадением диаметров волокон и числовых апертур.
Следует отметить, что потери на сращивание являются направленными,
по отношению к этим переменным (т.е. потери имеют место только, если оптический поток распространяется через сросток в направлении принимающего во-
156
локна, имеющего меньшие диаметр и апертуру). Потери на сращивание являются аддитивными, т.е. если сращиваются два многомодовых волокна, демонстрирующие несовпадение как в диаметрах сердцевины, так и в числовых апертурах, то их вклад в эти характерные потери является суммой этих двух потерь.
Рисунок 6.4– Характерные потери на сращивание, вызванные несовпадением диаметров волокон и числовых апертур
Как видно из рис. 3.5, фактические потери на сращивание (среднее от потерь по двум направлениям) оказываются практически ненаправленными. Другими словами, потери, зависящие от параметров волокна и рассматриваемые в
плане распространения света через сросток, не зависят от того с какой стороны
сростка распространяется световой поток). Нужно иметь в виду, что эти потери
достаточно малы для тех допусков на несовпадение MFD, которые декларируют
производители. Например, эти потери можно оценить в худшем случае на уровне
0,04 дБ дополнительных потерь для волокна, имеющего MFD, равный 9,3±0,5
мкм, в соответствии со спецификацией. Существуют и другие дополнительные
факторы, влияющие на механическое сращивание. Они включают расщепление
концов волокна, загибание волокна на конце и отражение Френеля.
В случае одномодовых волокон без сдвига дисперсии доминирующим фактором является несовпадение диаметров поля моды (MFD) волокон. На рис. 6.5
можно оценить вклад в этот вид потерь за счет несовпадения MFD.
Существуют также факторы, сопутствующие процессу сращивания. Они
привносятся методами и процедурами сращивания. К ним относятся продольные
и угловые смещения, загрязнение и деформация сердечника. Их влияние может
быть сведено до минимума за счет использования опытных техников, оборудования для автоматического выравнивания волокна и нескольких циклов плавления при работе на более современном оборудовании.
157
Подготовка оптического кабеля для сращивания включает следующие
этапы: зачистку волокна, очистку поверхности и формирование концевого угла
волокна.
Рисунок 6.5 – Характерные потери на сращивание для одномодового волокна,
вызванные несовпадением диаметров поля моды
Оболочку волокна можно удалить различными способами, например, химически путем, использованием оборудования термической или механической
зачистки. Для типичного акрилатного покрытия волокна, компания Corning рекомендует механическую зачистку, как наиболее надежную, быструю, дешевую
и создающую четко определенные условия терминирования оболочки.
Очистка поверхности – очень важный этап. Любые остатки акрилатного
покрытия после зачистки оболочки должны быть удалены с поверхности зачищенного участка волокна. Необходимо избегать любых операций по ручной обработке указанного участка волокна до тех пор, пока процесс сварки не будет
окончательно завершен. Это позволит минимизировать шанс загрязнения волокна пылью или жирными пятнами с рук, которые могут вызвать дополнительные потери сростка и уменьшение его прочности на растяжение.
Один из основных моментов, влияющих на качество сростка при одном
цикле плавления, является концевой угол. Поэтому надлежащее формирование
концевого угла является одним из основных шагов в получении приемлемого
сростка. Требования к концевому углу волокна могут меняться от пользователя
к пользователю и от типа используемого скалывателя. В общем случае, однако,
концевые углы волокна меньшие, чем два градуса, обычно приводят к приемлемым сварным сросткам. Можно ожидать, что хорошие типы скалывателей позволяют получить конечные углы волокна величиной в половину градуса.
Выравнивание волокна. Существуют блоки ручного и автоматического выравнивания волокна при сварке. Сначала оператор помещает очищенные и сколотые волокна в блоки выравнивания и/или другие механизмы фиксации волокна в устройстве сращивания. После этого волокна выравниваются визуально
путем перемещения их в направлении координат X-Y. Визуальное выравнивание
158
требует поддержания минимального возможного зазора между волокнами,
чтобы уменьшить видимые ошибки, которые возможны при ручном выравнивании краев волокон, проводимом при увеличении.
В случае автоматического выравнивания, начальное выравнивание состоит лишь в помещении концов волокон в зажимы V-образных канавок. Блок
выравнивания сам выравнивает волокна.
Существует пять возможных альтернатив для окончательного выравнивания сердцевины волокон:
1. Мониторинг мощности (светового потока), используя источник и приемник света.
2. Использование для такого мониторинга оптического рефлектометра
(OTDR).
3. Использование техники локального ввода и обнаружения (LID) (светового излучения).
4. Использование техники выравнивания профилей.
5. Пассивное выравнивание V-образных канавок.
Техника мониторинга мощности потока основана на оптимальном выравнивании волокон по уровню мощности, переданной через точку сращивания. Источник света при этом подсоединяется к входному концу одного из волокон, подлежащему сварке. Световой сигнал проходит через контакт волокон и его уровень считывается на измерителе мощности, подсоединенном к выходному концу.
Выравнивание достигается перемещением волокон в направлении X-Y до тех
пор, пока не будет достигнут максимум считываемой мощности. При этом способе выравнивания требуются два человека. Один – считывает показания приемника, тогда как другой (на некотором удалении от него) – оперирует с волокнами,
подлежащими сварке. Этот метод дает возможность улучшить визуальное выравнивание, так как позволяет оптимально выровнять сердцевины волокон, а не
оболочки.
В методе, описанном выше, вместо измерителя мощности может быть использован оптический рефлектометр (OTDR). Следует заметить, что выравнивание с использованием OTDR, зависит от возможности обеспечить в реальном
времени отображение уровня мощности для осуществления ее оптимизации.
Многие устройства сращивания используют систему локального ввода и
обнаружения светового излучения (LID). Это еще одна система выравнивания по
уровню мощности, но сформированная на месте сварки. Она исключает необходимость удаленного (на определенное расстояние) мониторинга уровня мощности. В этой системе волокна, расположенные по обе стороны от точки сварки,
загибаются вокруг цилиндрических оправок, которые достаточно малы, чтобы
позволить осуществить ввод (в точка входа) и вывод (в точке выхода) светового
излучения через оболочку волокон.
Системы выравнивания профиля формируют изображение места сварки,
чтобы дать возможность техникам надлежащим образом выровнять два волокна
159
для сварки. Коллимированный пучок направляется под прямым углом к оси свариваемых волокон в место сварки. Это создает образ волокна, которое должно
быть выровнено. Один из специальных типов устройств выравнивания создает
сгенерированный компьютером образ центральной линии сердечников, к которому компьютер и приводит два волокна перед тем, как осуществить сварку.
Другая система выравнивания профиля выполняет процедуру выравнивания, используя профиль оболочки волокна. Нужно иметь ввиду, что качество выравнивания при этом во многом зависит от концентричности системы сердечникоболочка. При использовании пассивного выравнивания V-образных канавок
само выравнивание волокна является результатом точного соответствия Vобразных канавок, диаметра оболочки волокна и концентричности системы сердцевина-оболочка.
Процедура сварки. Процесс сварки использует электрическую дугу для
разогрева и сваривания. Некоторые техники используют один или несколько коротких включений тока дуги для того, чтобы удалить любые возможные загрязнения из волокна в месте сварки перед началом сварки.
Следующим шагом является предварительная сварка. Этот процесс состоит в нагревании волокна для размягчения его соединяемых концов. Предварительная сварка осуществляется для того, чтобы концы волокна были при температуре, оптимальной в процессе последнего шага сварки, что дает возможность материалу волокон течь навстречу друг друга вплоть до момента физического контакта. Если температура на стадии предварительной сварки слишком велика, то может возникнуть излишняя деформация концов волокон, что в свою
очередь приведет к изменению геометрии стекла. Если же эта температура слишком мала, то может возникнуть механическая деформация концов волокон. В
этом случае может произойти выпучивание волокна в тот момент, когда на последней стадии сварки на концы волокон будут действовать силы, стягивающие
их.
Оптимальная подготовка к сращиванию включает установку тока дуги и ее
длительности, установку длины зазора и перекрытия шагов предварительной и
окончательной сварки. Эти установки должны быть определены (экспериментально) на основании результатов последовательности сварок.
Качество сварки включает два основных параметра, как это отмечалось
выше, а именно: прочность волокна на растяжение и потери, вносимые в месте
сварки. Некоторые устройства сращивания имеют возможность осуществлять
тесты на растяжение. Опытные техники знают, как осуществить такое испытание
вручную, чтобы простыми средствами оценить прочность на растяжение.
Потери на сращивание могут быть проконтролированы с помощью удаленного OTDR или измерителя мощности аналогично тому, как это делалось выше
для выравнивания волокна. Точные измерения потерь сростка с помощью OTDR
требуют усредненных двунаправленных измерений.
160
6.5 Волоконно-оптические элементы ветвления потока (разветвители)
6.5.1. Введение
Элементы ветвления потока либо разделяют световой поток на несколько
путей (направлений), либо, наоборот, соединяют несколько световых потоков в
один путь (направление). Некоторые из этих устройств, которые выполняют эту
функцию, называют разветвителями (couplers). Ниже перечислены различные
типы таких устройств и кратко описаны выполняемые ими функции.
Комбайнер (combiner) – устройство, обычно имеющее один выходной порт
и два или больше входных портов. Он может быть использован для осуществления как однонаправленных, так и двунаправленных операций.
Сплиттер (splitter) – устройство, имеющее обычно один входной порт и несколько выходных портов. Он может быть использован для двунаправленной передачи или для распределения потока на два или большее число устройств или
конечных пользователей.
Древовидный разветвитель (tree coupler) – устройство, принимающее поток (сигнал) на один вход и распределяющее его несколько выходов и наоборот.
Как правило оно используется для распределения сигнала от одного источника
ко многим пользователям.
Звездообразный разветвитель (star coupler) – многопортовое устройство,
имеющее, по крайней мере, два входных порта и два или более выходных портов.
Оно может распределять или объединять сигналы с множества входных портов
в один выходной порт, или принимать световой сигнал и распределять его на
множество выходных портов.
Широкополосный разветвитель (или же разветвитель, нечувствительный к
длине волны) – устройство, работающее в двух окнах прозрачности: 1310 и 1550
нм. Соответственно все аналогичные элементы ветвления должны иметь возможность работать в этих двух окнах. Другая желаемая особенность таких элементов ветвления – быть невосприимчивым к изменению рабочих длин волн
внутри одного окна. Другими словами, вносимые потери должны быть одинаковы для любой длины волны в одном из окон.
Разветвитель доступа, или ответвитель (tap) – трех или четырехпорто-вое
устройство ответвления для облегчения осуществления функций ввода-вывода
обычно с малым уровнем оптической мощности. Его коэффициент ответвления
в высшей степени неоднороден. Этот тип устройств может быть использован в
гибридных (медь-волокно – HFC) кабельных сетях, для мониторинга статуса линии и для мультиплексоров ввода вывода.
Мультиплексоры-демультиплексоры с разделением по длине волны –
устройства ветвления формально ничем не отличающиеся от разветвителей. Эти
устройства распределяют световой сигнал в зависимости от длины волны. Мультиплексор используется для передачи нескольких световых сигналов (каждый на
161
своей длине волны) по одному волокну. Демультиплексор принимает агрегированный световой сигнал, распространяющийся по одному волокну и разделяет
его на несколько компонентов в зависимости от длины волны так, что каждая
компонента направляется в отдельное волокно.
Компоненты ветвления светового потока находят широкое применение в
локальных сетях, где средой передачи является оптоволокно. Разветвители обеспечивают двунаправленную передачу между магистральным ВОК и станцией
ЛВС. Разветвители нашли также применение в широкополосных беспроводных
радиосетях, называемых локальными системами многоточечного распределения
(LMDS). В этих сетях они подключают оптоволоконную магистраль к узлу
LMDS, который содержит мультиплексор ввода-вывода, устройство управления
доступом и радиотерминалы. Разветвители также широко используются в оптических коммутаторах.
6.5.6. Концепции разветвителей/элементов ветвления
Рассмотрим рис. 6.6. Он показывает, что может произойти, если мы поместим два отрезка оптоволокна, контактирующих бок о бок, в открытый огонь и
превратим их сплавной разветвитель с биконический отводами. Внутри каж дого
волокна существует длинная секция ответвлений, затем однородная секция
длины Z, где они сплавляются (свариваются), а затем еще одна секция ответвлений, с направленным обратно по отношению к первой, кросс-соединением двух
отдельных волокон.
Рисунок 6.6 – Схематичное изображение сплавного биконического разветвителя. Обратите внимание, что в области связи длиной Z сердцевины сжаты и
поле «выдавливается в воздушную оболочку»
Эти ответвления достаточно плавные, так что только незначительная часть
энергии падающая из любого порта, расположенного слева, отражается назад в
любой из портов, расположенных справа. По этой причине указанные устройства
часто называют направленными разветвителями.
Используя эту технологию, можно сделать ряд разветвителей, основанных
на том, что уровень мощности, перешедшей из одного волокна в другое, может
быть изменен путем изменения следующих параметров: Z– длины области связи,
через которую осуществляется взаимодействие двух полей; а – радиуса сердцевины в области связи; Да – разности радиусов сердцевин в области связи. Созданные на базе этой концепции различные типы разветвителей будут описаны
ниже.
162
Моды низкого порядка продолжают существовать в исходном волокне до
тех пор, пока угол падения остается больше критического угла. На выходе оболочечные моды конвертируются обратно в моды сердцевины. При этом коэффициент раветвления определяется длиной разветвителя (в нашем случае – Z, см.
рис. 6.6) и толщиной оболочки.
Типичный вариант расветвления мощности в этом случае может быть
50:50, когда одна половина мощности идет на один выходной порт, а другая - на
другой. При первом (грубом) варианте анализа выходной мощности разветвителя дает следующее. Допустим, что уровень мощности входного сигнала равен
–10 дБм, тогда на каждом из выходов мы, казалось бы, должны получить уровень
–13 дБм, что выглядит логично. Однако мы забыли про вносимые потери. Это те
внутренние потери, которые вносит сам раз-ветвитель за счет рассеивания мощности внутри него самого. Типичное значение таких потерь - 0,7 дБ. Следовательно, уровень мощности на выходах разветвителя составит –13,7 дБм. Этот тип
разветвителя мощности является частью основного класса разветвителей, базирующихся на концепции сплавного разветвителя с биконическими отводами, описанного выше. Многие типы разветвителей могут быть сделаны на основе такого
разветвителя, как разветвитель мощности, показанный на рис. 6.7: комбайнеры,
Y-переходы, звездообразные разветвители, направленные разветвители и т.д.
Рисунок 6.7 – Разветвитель на основе многомодового волокна
На рис. 6.8 показан разветвитель, который работает с одномодовым волокном, но является зависимым от используемой длины волны. Когда два разветвителя в варианте с биконическими отводами находятся в тесном контакте друг с
другом, как на рис. 6.8, возникает резонансное явление. Световой поток волокна
А захватывается сердечником волокна В. Уровень мощности, переданный в волокна В и А, зависит от длины области связи. Световой поток из волокна А может
быть захвачен на 100%, т.е. полностью перейдет в волокно В на определенной
длине, называемой длиной области связи, или на длине нечетно кратной ей.
Длина области связи изменяется в зависимости от длины волны света в волокне.
Величина коэффициента разветвления при этом может быть настроена путем выбора нужной длины области связи.
163
Рисунок 6.8 – Оптический разветвитель на основе одномодового волокна
Важным является следствие того факта, что длина области связи зависит
от длины волны света в одномодовом разветвителе. Предположим, что мы передаем по волокну две длины волны: 1300 и 1550 нм. Требуемая длина области
связи, для длины волны 1550 нм, больше, чем для длины волны 1300 нм. Это
приводит к тому, что свет с длиной волны в 1300 нм полностью (100%) перейдет
в сердцевину волокна В из А, а затем вернется из В в сердцевину волокна А. Свет
длины волны 1550 нм также полностью (100%) перейдет в сердцевину волокна
В из А. Тщательно выбирая длину области связи, можно добиться объединения
или разделения двух длин волн. Эта концепция иллюстрируется рис. 6.9.
Рисунок 6.9 – Разветвитель на основе одномодового волокна,
показан процесс разделения длин волн
На рис. 6.10 показан разветвитель, работающий как Y-переход, или разветвитель мощности 1x6. В этом случае, в идеале, световой поток разделяется поровну между двумя выходными плечами. Y-переходы трудно осуществить путем
сращивания трех волокон, и, к тому же, полученное устройство будет иметь
большие потери. Более практично было бы создать оптические волноводы со
стеклянной подложкой.
Рисунок 6.10 – Y-переход или разветвитель 1х2
Y-переходы можно состыковывать для создания разветвителей 1x4 или
1x8, как показано на рис. 6.11.
164
Рисунок 6.11 – Стыковка Y-переходов друг с другом
6.5.3. Рабочие параметры разветвителей/элементов ветвления
В табл. 6.2 приведены функциональные параметры передачи для волоконнооптических разветвителей, или элементов ветвления.
Таблица 6.6. Параметры передачи для разветвителей/элементов ветвления
Параметры
Вносимые потери (дБ)
Оптическое отражение (дБ)
Диапазон рабочих длин волн (нм)b)
Потери, зависящие от поляризации (Δ дБ)
Направленность (дБ)
Однородность (дБ)
Максимум
4,0 log2n
-40
1580/1360
0,1(1+ log2n)
неприменимо
1,0log2n
Все сети
Минимум
неприменимо
неприменимо
1480/1260
неприменимо
50
неприменимо
a) Заметим, что устройства 2 х и для 2  n  32 находятся в стадии разработки.
b) Предполагается работа в одной или в обеих полосах пропускания; однако, если существует некая длина волны, выходящая за границу полосы пропускания, то значения таких параметров, как потери, применимо для нее только
в этой ограниченной полосе.
6.5.4. Основные определения разветвителей/элементов ветвления
Коэффициент разветвления. Коэффициент разветвления (coupling ratio),
или коэффициент расщепления (splitting ratio), определяется как отношение оптической мощности, излучаемой одним выходным портом, к сумме оптических
мощностей, излучаемых всеми выходными портами. Коэффициент разветвления
измеряется на определенной центральной длине волны. Многомодовые разветвители измеряются с равновесным модовым заполнением.
Центральная длина волны и полоса пропускания. Показатели всех развет-вителей меняются в зависимости от длины волны. Спецификация разветви-телей
обычно распространяется на все окно прозрачности или, в некоторых случаях,
на несколько окон. Центральная длина волны является лишь номинальной рабочей длиной волны разветвителя, тогда как полоса частот является диапазоном
длин волн, в рамках которого эта спецификация гарантируется.
165
Критерий выбора полосы пропускания, рекомендуемый компанией
Telcordia, состоит в следующем.
Для не-WDM приложений, работающих в диапазонах 1310/1550 нм и с
WDM-элементами ветвления, для всех цифровых приложений, кроме SONET с
длинными секциями, должны выполняться следующие требования по ширине
обоих рабочих полос в длинноволновой области:
1260 - 1360 нм и 1480 - 1580 нм
Для приложений WDM и SONET с длинными секциями рекомендуемые
полосы следующие:
1280 - 1335 нм и 1525 - 1575 нм
Для DWDM рекомендуемые полосы следующие:
1285 - 1325 нм и 1530 - 1566 нм
Для гибридных систем, использующих модуляцию АМ-ЧПБП, рекомендуемые полосы следующие:
1290 - 1330 нм и 1530 - 1570 нм
Следует заметить, что разработчики оптоволоконных элементов рекламируют в настоящее время различные устройства, частотный диапазон которых
простирается много дальше 1600 нм.
Вносимые потери. Определения и обсуждение потерь см. раздел 6.3.1.
Типичные избыточные потери. Избыточные потери – это отношение оптической мощности, поступающей на входной порт разветвителя, к общей мощности
на выходе любого выходного порта, выраженное в дБ. Типичные избыточные
потери – это ожидаемое значение избыточных потерь, измеренное на определенной центральной длине волны. Для многомодовых разветвителей измерения проводятся с равновесным модовым наполнением (EMF).
Избыточные вносимые потери. В оптическом волноводном разветвителе избыточные вносимые потери – это оптические потери, ассоциируемые с той порцией света, которая не излучается из номинально функционирующих портов
данного устройства.
Однородность. Однородность является мерой того, насколько выходная
мощность равномерно распределена между выходными портами разветвителя.
Понятие однородности применяется к разветвителям с номинально равными коэффициентами разветвления и определяется как разность между максимальными
и минимальными вносимыми потерями, оцененная на множестве всех выходных
портов рассматриваемого разветвителя и выраженная в дБ. Однородность задается типовым значением для полосы пропускания в целом. Дополнительные рассуждения относительно однородности приведены в разд. 6.3.9.
Telcordia определяет однородность L как максимальную вариацию вносимых потерь между одним входным портом i и любыми двумя выходными портами j и к, или между входными портами j и к и одним выходным портом i.
Элементы ветвления, которые предполагается использовать в цифровых
системах, работающих на скоростях до 10 Гбит/с, должны иметь следующую однородность:
166
L  0,8 log 2 N ,
где N – число портов разветвителя.
Для систем АМ-ЧПБП однородность определяется так:
L  0,5 log 2 N .
Однородность особенно важна для систем DWDM и АМ-ЧПБП.
Направленность, возвратные потери, отражательная способность. Направленность является отношением оптической мощности, поступающей на входной
порт, к оптической мощности, возвращенной с любого другого входного порта.
Направленность понимается как степень изоляции на ближнем конце, или перекрестная помеха на ближнем конце. Возвратные потери являются отношением
оптической мощности, поступающей на входной порт, к оптической мощности,
возвращенной с того же входного порта. Как направленность, так и возвратные
потери, выражаются в дБ (положительные значения) и измеряются при условии,
что все выходные порты оптически терминированы (заглушены). Отражательная
способность численно равна возвратным потерям, но имеет противоположный
знак. Во многих случаях отражательная способность и возвратные потери используются как синонимы. Минимальные значения направленности и возвратных потерь являются теми нижними пределами, которые распространяются на
весь диапазон длин волн, определенный в полосе пропускания. Дополнительные
рассуждения относительно отражательной способности приведены в разд. 6.3.3.
6.5.5. Звездообразные и направленные разветвители/элементы ветвления
– дополнительное обсуждение
Звездообразныеразветвители имеют больше четырех портов. Существуют
два типа таких разветвителей: звездообразный разветвитель передающего типа и
звездообразный разветвитель отражающего типа. Звездообразный разветвитель
передающего типа показан на рис. 6.16.
Рисунок 6.12 – Звездообразный разветвитель передающего типа
Световой поток, поступающий на один из входных портов звездообразного
разветвителя передающего типа, разветвляется на все выходные порты равномерно. Например, на рис. 6.12, свет, поступающий на входной порт Е, разветвляется на выходные порты G, H, I, J, К и L.
167
Рисунок 6.13 – Звездообразный разветвитель отражающего типа. Напоминает архитектуру звезды пассивной ЛВС
Существуют направленные ответвители с топологией дерева и ветви с коэффициентом расщепления 1 х N, 2 х 6. Направленность достигается с одним
основным портом ввода-вывода и двумя ответвленными портами ввода-вывода.
Основное волокно (ствол дерева) может передавать оптическую мощность в двух
направлениях. Ответвленные порты при этом являются однонаправленными –
оптическая мощность направляется в них к основному или от основного волокна.
На рис. 6.13. показан звездообразный разветвитель отражающего типа.
6.6 Оптические аттенюаторы
Аттенюатор – устройство, которое уменьшает интенсивность светового сигнала, прошедшего через него. Аттенюаторы часто используются в качестве звена
в схеме после лазерного передатчика, чтобы согласовать его выходную мощность с уровнем, требуемым следующими за ним в этой схеме устройствами, такими как усилители EDFA. Нужно тщательно выбирать тип аттенюаторов так,
чтобы они имели отличные параметры возвратных потерь (их уровень д. б. > 40
дБ), чтобы быть уверенным, что уровень света, отражаемого обратно в направлении передатчика, будет очень низок. Другими ключевыми параметрами аттенюаторов являются:
 стабильность;
 надежность;
 оптические возвратные потери (ORL);
 потери, зависящие от поляризации (PDL);
 точность;
 повторяемость;
 вносимые потери;
 поляризационная модовая дисперсия (PMD).
168
Одно из наиболее простых применений – короткие оптоволоконные секции, где
уровень интенсивности света настолько высок, что выходит за границы динамического диапазона детектора света (приемника). В такой схеме можно поставить аттенюатор, для уменьшения интенсивности света до уровня, соответствующего динамическому диапазону используемого приемника.
Другим примером является применение аттенюатора в системах WDM, где
мощность каждого канала подстраивается так, чтобы обеспечить плоскую спектральную характеристику светового сигнала, поступающего на первый в линии усилитель
EDFA. Следовательно, плоская спектральная характеристика в пределах ширины полосы канала также является ключевым параметром аттенюатора.
Существуют оптические аттенюаторы с переменным (VOA) и фиксированным
коэффициентом ослабления, иногда называемые демпфирующими прокладками.
6.6.1. Основные рабочие параметры аттенюаторов
Допуск на вносимые потери должен быть не больше, чем ±15%. Для аттенюаторов с фиксированным коэффициентом ослабления обычно используется следующий ряд коэффициентов ослабления (вносимых потерь): 3, 5, 10, 15, 20, 25, 30 дБ.
Значение оптической отражательной способности должно, максимально, быть на
уровне –40 дБ. Диапазон рабочих длин волн аттенюаторов должен составлять, максимально, от 1360 до 1580 нм, минимально – от 1260 до 1480 нм. Типичная ширина
полосы рабочих длин волн составляет 1310-1580 нм. Уровень потерь аттенюаторов,
зависящий от поляризации (PMD), не должен быть выше 0,3 дБ.
6.7 Изоляторы, их параметры
Изоляторы – устройства, для которых потери света малы при распространении
в одном направлении и велики в противоположном направлении. Изоляторы обычно
устанавливают в выходных схемах устройств с высоким уровнем интенсивности
света, таких как передатчики на лазерных диодах и усилители EDFA. Их функция –
уменьшить уровень сигнала, отраженного назад в используемый лазерный диод или
усилитель EDFA.
Характеристики изолятора определяются следующими критическими параметрами:
 спектральной зависимостью, особенно для так называемых узкополосных
изоляторов, которые проектируются для работы в спектральном диапазоне уже, чем
20 нм. Изоляторы описываются пиком ослабления обратного излучения и шириной
полосы, лежащей в области 3 дБ ослабления уровня изоляции от максимума этого
пика.
 малым уровнем вносимых потерь, < 1 дБ в прямом направлении, и большим уровнем потерь в обратном направлении: больше 35 дБ (при одноступенчатой изоляции) и 60 дБ (при двухступенчатой изоляции), и слабой зависимостью
от поляризации.
169
 поляризационной модовой дисперсией (PMD). Изоляторы обычно проектируются на основе использования элементов с высоким уровнем двойного лучепреломления, а они весьма склонны к высокому уровню PMD (типичное значение – 50-100 фс, 1фс = Ю-15 с), в особенности для одноступенчатого изолятора.
Двухступенчатые изоляторы могут быть спроектированы так, что PMD, вносимая первой ступенью, во многом компенсируется второй ступенью.
 потерями, зависящими от поляризации (PDL). Они ухудшают характеристики оптического изолятора.
В общем случае при проектировании изоляторов используют эффект Фарадея. Он управляет вращением плоскости поляризации оптического луча в присутствии магнитного поля. Это вращение происходит в том же направлении, что
и направление распространение света, параллельно или антипараллельно
направлению магнитного поля. Оптический изолятор состоит из цилиндрического стержня из материала с эффектом Фарадея, такого как железоиттриевый
гранат (YIG), длина которого выбирается так, чтобы обеспечить вращение на
45°. Этот цилиндрический стержень помещается между двумя поляризаторами,
чьи оси скрещены на 45° относительно друг друга. Свет, распространяющийся в
одном направлении, проходит через второй поляризатор благодаря эффекту Фарадея. В отличие от этого, свет, распространяющийся в противоположном
направлении, блокируется первым поляризатором. Уровень изоляции должен
быть больше, чем 30 дБ. Отражательная способность оптического изолятора
должна быть на уровне 40 дБ и выше.
Оптические изоляторы или вентили - устройства, пропускающие свет
только в одном направлении. Они широко применяются в различных устройствах волоконно-оптических систем, в частотности в волоконно-оптических усилителях. В аналоговых системах ВОЛС применяются полупроводниковые лазеры со встроенными оптическими изоляторами. Такие лазеры применяются
также и в высокоскоростных системах передачи SDH, в системах с OTDM, в многоволновых системах DWDM, в которых применяются удаленные ВОУ с дистанционной накачкой по отдельному волокну.
Принцип работы оптического вентиля основан на явлении вращения плоскости поляризации света при прохождении его через некоторые вещества, чувствительные к магнитному полю. Наибольшая чувствительность проявляется в
том случае, когда магнитные силовые линии перпендикулярны направлению
распространения света. Если тело, изготовленное из такого вещества, имеет
длину L, то угол поворота плоскости поляризации уу определяется из выражения:
   LH,
(6.4а)
где:  - постоянная Верде, H - напряженность магнитного поля. Поскольку явление поворота плоскости поляризации в магнитном поле открыл Фарадей, иногда оптический изолятор, основанный на использовании этого явления, называют фарадеевским.
170
На рис. 6.13а а представлена схема работы оптического изолятора. Неполяризованный луч света направляется на поляризатор 1, пропускающий плоскополяризованное излучение Р  , затем проходит через фарадеевский элемент 2 с
постоянной Верде  , находящийся в перпендикулярном магнитном поле Н, создаваемом постоянным магнитом 3. На выходе этого элемента 2 плоскость поляризации луча повернется на угол  , определяемым постоянной р, длиной элемента 2 - L и величиной Н. Значения этих параметров выбираются такими, чтобы
угол поворота уу был равен 45°. Таким образом, элемент 4 в данном случае играет роль поляризационного анализатора. Если теперь с другой стороны, справа,
направить луч, то та его составляющая, плоскость поляризации которой совпадает с плоскостью поляризации элемента 4, проходит через него и вводится в
фарадеевский элемент 2, в котором плоскость поляризации поворачивается еще
на 45°. Таким образом, попадая справа на элемент 1, плоскость поляризации луча
оказывается развернутой по отношению к входному лучу на 90°, вследствие чего
поляризатор 1 его не пропускает.
Необходимо отметить, что излучение, распространяющееся в ОВ, как правило, неполяризованное. Поэтому при прохождении через поляризатор теряется
половина мощности излучения (3 дБ). На рис. 6.13, б представлена схема оптического изолятора, применяемая на практике, где 1 - оптический элемент с анизотропными свойствами, благодаря которым неполяризованный луч расщепляется на два ортогонально поляризованных луча - с перпендикулярной плоскостью поляризации (обыкновенный луч) и с параллельной - необыкновенный луч,
(в качестве такого элемента может служить призма, напри-
171
Рисунок 6.13а – Схема оптического изолятора
Рисунок 6.13б – Общий вид оптического изолятора фирмы SAMSUNG
мер, Николя или Рошона). Оба луча направляются на фарадеевский элемент 2,
на выходе которого плоскость поляризации поворачивается на 45°. После этого
оба луча направляются также на призму 4, развернутую по отношению к призме
1 на 45°. Поскольку призмы 1 и 4 обладают свойством обратимости, то на выходе
призмы 4 излучение будет неполяризованным. Если теперь излучение на призму
4 направить справа, то, пройдя через эту призму и элемент 2, плоскость поляризации каждого луча (обыкновенного и необыкновенного) повернется еще на 45°,
так что к элементу 1 оба луча подойдут с плоскостями поляризации, развернутыми на 90° по отношению к входным, вследствие чего через призму 1 они не
пройдут.
В настоящее время элемент 2 для оптических изоляторов выполняется из
железоиттриевого граната YIG, или более подходящего материала на основе двуокиси титана ТiO2 + СаСO6. Современные оптические изоляторы имеют потери
мощности излучения в прямом направлении менее 1 дБ, в обратном - более 50
дБ. Конструктивно оптические изоляторы выполняются в виде цилиндра диаметром 8...10 мм и длиной 30...60 мм. На рис. 6.13б представлен общий вид оптического изолятора производства фирмы SAMSUNG.
172
6.8 Волоконно-оптические фильтры
Оптические фильтры используют механизм селекции длин волн и могут
быть грубо разделены на две большие категории в зависимости от того, какой
физический механизм положен в их основу: оптической интерференции или дифракции. Существуют фильтры, рассчитанные на выделение фиксированной
длины волны, и настраиваемые фильтры. Для настраиваемых фильтров желательно иметь следующие свойства:
 широкий диапазон настройки для максимизации числа каналов, которые
могут быть выбраны;
 незначительные перекрестные помехи, чтобы избежать помех от соседних каналов;
 быстрая настройка для минимизации времени доступа;
 малые вносимые потери.
Фильтры выполняют исключительно важную роль в оборудовании WDM/
DWDM на стороне демультиплексора. Стандарт ITU-T G.671 рекомендует следующие значения параметров фильтров:
Вносимые потери: максимум 1,5 дБ в полосе пропускания; Вносимые потери: минимум 40 дБ в полосе задерживания; Оптическая отражательная способность: –40 дБ.
6.9 Элементы коммутации и коммутаторы
Коммутационные панели как устройства чрезвычайно просты. Это пассивные панели, которые имеют набор адаптеров (розеток), для соединения с помощью кабелей и их разъединения. Большинство коммутационных панелей допускает возможность подсоединения кабелей с двух сторон, что позволяет достичь
большей гибкости при реконфигурации оптических кабелей. Другие коммутационные панели обеспечивают управление кабельным хозяйством, так чтобы сохранить в должном порядке вариант маршрутизации и расположение кабелей.
Коммутационные панели используются также как схемы точек доступа для
тестирования и поиска неисправностей. Они используются для реконфигурации
оборудования. Если, например, оборудование, или устройство, вышло из строя,
то надлежащим образом скоммутированная панель позволяет персоналу легко
перенаправить поток с пострадавшего соединения на резервное или на другое
оборудование.
Распределительные блоки и шкафы аналогичны коммутационным панелям
и отличаются только тем, что имеют дополнительное пространство и позволяют
организовать раскладку волокна. Всегда рекомендуется оставлять некоторый тех-
173
нологический запас волокна. Этот запас может пригодиться, если придется изменить схему соединения. Распределительные блоки обеспечивают место для хранения этого запаса волокна в виде достаточно большой бухты кабеля.
Кроссы, или кросс-соединители//кросс-коммутаторы, существуют в нескольких модификациях. Некоторые техники и полевые инженеры используют
термин кросс как синоним коммутационной панели, в которой все операции осуществляются вручную. Мы определим кросс как синоним переключателя световой волны (то есть как синоним кроссс-коммутатора).
Основная цель кросс-коммутатора в сети – реорганизовать звенья связи.
Они выполняют изменение маршрута сигнала и используются для конфигурации маршрута или восстановления звена связи. Эти коммутаторы автоматически работают в оптической области, будучи сконфигурированы какими-то
управляющими воздействиями. Они используются также в оптических мультиплексорах ввода-вывода. Кроме того они могут быть использованы в оптических маршрутизаторах, осуществляющих маршрутизацию в зависимости от
длины волны. Ключевыми параметрами, определяющими показатели коммутаторов и, следовательно, их пригодность для тех или иных приложений, являются:
 вносимые потери и потери на разветвление;
 возвратные потери;
 потери, зависящие от поляризации;
 перекрестные помехи и уровень изоляции;
 надежность;
 время переключения;
 стабильность;
 степень сложности.
В табл. 6.3 перечислены значения параметров передачи для оптических
коммутаторов, они взяты из стандарта ITU-T G.671.
Таблица 6.3 – Параметры передачи, рекомендуемые для оптических коммутаторов
Параметры
Вносимые потери, дБ
Переключатели типа
Переключатели типа
a)
1хn
2x2
Максимум
Минимум
Среднее
Стандартное
не применимо изучается
не применимо
2,5//1og2n
Отражательная способность, дБ
Рабочий диапазон волн,
нм
Потери, зависящие от поляризации, ЛдБ
-40
не применимо
-40
не применимо
изучается
изучается
изучается
изучается
изучается//
не применимо
изучается
не применимо
Время переключения, мс
20//10
не применимо
изучается
не применимо
Повторяемость, дБ
0,25
не применимо
изучается
не применимо
174
0,1(1 + log2n)
Однородность, дБ
изучается//
не применимо
изучается
не применимо
0,41og2n
Переходные помехи, дБ
не применимо
Изучается b)
изучается
не применимо
Направленность, дБ
не применимо
50
изучается
не применимо
Двойные значения (а//b) приведены: а – для медленных коммутаторов, b –
для быстрых коммутаторов
b)
Рассматривается величина 25 дБ, решение зависит от согласованного определения перекрестной помехи.
a)
175
7 КОМПОНЕНТЫ КОММУТАЦИИ
И МУЛЬТИПЛЕКСИРОВАНИЯ
7.1 Введение
Одна из основных операций в системах WDM - мультиплексирование-демультиплексирование оптических несущих. Параметром, по которому она осуществляется, является длина волны, поэтому данная операция (а вместе с ней и
технология WDM в целом) носит название операции оптического мультиплексирования с разделением подлине волны (WDM), или, более кратко, операции волнового мультиплексирования.
Эта операция делится на два этапа: этап мультиплексирования и этап демультиплексирования.
Операция оптического мультиплексирования математически описывается
функцией суммирования: 1i, где 1i - модулированные оптические несущие (i= 1,
2.....n), спектры которых не перекрываются и шаг между номинальными центральными частотами постоянен. При этом процесс суммирования может осуществляться последовательно с использованием функции пространственного интерливинга (перемежения, или чередования, несущих). Она напоминает функцию временного интерливинга и позволяет решать, например, задачу мультиплексирования 80 (или п) несущих с шагом по сетке частот WDM 50 ГГц (или h)
последовательно в два этапа. На первом этапе мультиплексируются две группы
по 40 (или n/2) несущих, включающих все четные (первая группа) и все нечетные
(вторая группа) несущие, расположенные в своих группах с шагом 100 ГГц (или
2h). На втором этапе две полученные группы мультиплексируются (суммируются) вместе. Указанная операция может быть также осуществлена и в 4 этапа,
при этом на первом этапе формируются (мультиплексируются) 4 группы с числом несущих n/4 и шагом несущих в группе 4h. Могут быть использованы и другие варианты. Реализация указанной функции, осуществляемая устройствами
интерливинга, или интерливерами, используется достаточно широко в системах
WDM с большим числом несущих, так как позволяет снизить требование на максимальное число одновременно мультиплексируемых несущих и упростить
мультиплексоры.
В соответствии со стандартами и IEC 61931-1 (6.52), "волновой мультиплексор (MUX) - это устройство ветвления с двумя или большим числом входных портов и одним выходным портом, такое где световой поток в каждом порту
ограничивается предварительно выбранным диапазоном длин волн, а выход является комбинацией световых потоков этих портов".
Операция оптического демультиплексирования сводится к разделению
всех несущих в точке терминирования агрегатного потока WDM. Эта задача является обратной по отношению к задаче мультиплексирования и может быть
решена, в принципе, теми же устройствами, если они обладают свойством обратимости, т. е. будучи (n+1 )-полюсниками (где полюс реализуется входным или
176
выходным оптическим портом), решают задачу мультиплексирования в конфигурации: n входов - 1 агрегатный выход, а задачу демультиплексирования в конфигурации: 1 агрегатный вход - n выходов при замене выходного полюса (для
оптических устройств агрегатного выходного порта) на входной, а входных полюсов (портов) на выходные. Таким свойством обладают большинство пассивных мультиплексоров-демультиплексоров, что делает универсальным их использование и позволяет анализировать только процесс демультиплексирования.
В соответствии со стандартами и IEC 61931 -1 (6.53), "волновой демультиплексор (DEMUX) - это устройство, которое выполняет операцию, обратную по
отношению к мультиплексору, такое, где вход является оптическим сигналом,
объединяющим два или большее число диапазонов волн, а выход каждого порта
соответствует различным предварительно выбранным диапазонам длин волн".
7.2 Элементы спектрального разделения оптических мультиплексоров
Агрегатный оптический сигнал, полученный в результате мультиплексирования, можно представить в виде амплитудно-волновой (АВХ) или амплитудно-частотной (АЧХ) характеристик гребенчатого фильтра, где каждый зубец
гребенки - это АВХ или АЧХ модулированной несущей. Центральные номинальные частоты несущих f0r такой гребенки в системах WDM (DWDM) соответствуют сетке частот, рекомендованной стандартами, с постоянным шагом h,
определяющим разнос несущих. Причем сетка стандарта, определенная для
опорной частоты 193,1 ТГц и минимального шага 50 ГГц, была (начиная с 2002
года) уплотнена до 12,5 ГГц и перенесена в рекомендацию. В результате каждой
несущей может выделяться окно (f0n-h/2, f0n+h/2) шириной h ГГц, выбираемое из
следующего ряда, ГГц: 12,5; 25; 50; 100; 200; 400; 600; 1000.
Последний шаг 1000 ГГц соответствует разносу по длине волны примерно
8 нм в окне 1550 нм, тогда как первый - соответствует 0,1 нм, что сравнимо с
температурными флуктуациями частот несущих, генерируемых лазерами. Для
того чтобы перекрыть такой широкий диапазон значений, используются различные технологии (или устройства) демультиплексирования.
В 1996-1999 годах произошел существенный прорыв в технологии мультиплексирования, обусловленный, с одной стороны, переходом к интегральным
оптическим технологиям, с другой - миниатюризацией и улучшением качества
изготовления элементов традиционной дискретной оптики и появлением промышленной микрооптики. В результате стало возможным разделить все демультип-лексоры на два больших класса: демультиплексоры на микрооптических
устройствах и на оптоволоконных направленных разветвите-лях(ОВНР).
Первый класс демультиплексоров использует микрооптику для реализации двух основных технологий мультиплексирования, основанных на разделении несущих с помощью фильтрации на основе интерференционных фильтров и
явления угловой дисперсии.
177
Нужно отметить, что эти технологии в целом отличаются от технологий
фильтрации, рассмотренных в работе применительно к мультиплексорам вводавывода, тем, что они нацелены на одновременную фильтрацию не единиц, а
большого числа каналов, несущие которых разнесены по сетке с постоянным шагом.
Для разреженных систем WDM (CWDM), согласно рекомендации, напротив, используется не частотный, а волновой план с постоянным и единственным
шагом сетки 20 нм. Можно сказать, что для них демультиплексирование (разделение) несущих не составляет проблем при использовании даже традиционных
методов оптической фильтрации, например многослойных фильтров на тонких
пленках.
Что касается "нового класса" широкополосных систем WDM (WWDM), то
они по определению не имели проблем демультиплексирования, так как использовали разнос несущих больше 20 нм. Это дало возможность мультиплексировать 2-4 несущие в одном волокне в окне прозрачности 1310 нм уже в 1987-1990
годах.
7.3 Технологии демультиплексирования систем WDM и DWDM
Итак, действительно проблемными с точки зрения демультиплексирования могут быть только системы WDM, плотные WDM (DWDM) и высокоплотные WDM (HDWDM), последний класс в рекомендации не выделен. Причем эти
проблемы растут обратно пропорционально используемому шагу между несущими и переходному затуханию АЧХ соседних несущих.
На основе вышеизложенного можно составить следующую классификацию технологий DMUX:
1. DEMUX на основе объемных микрооптических устройств, использующих:
а) интерференционные фильтры
•на основе резонатора Фабри-Перо (FP),
•на многослойных диэлектрических тонких пленках (DTF),
•на отражательных оптоволоконных решетках Брэгга (FBG);
б) явление угловой дисперсии •в трехгранной призме,
•на дифракционной решетке.
2. DEMUX на основе пленарных интегральных устройств, использующих:
а) оптоволоконные направленные разветвители (ОВНР);
б) интерферометры Маха-Цендера (MZI);
в) дифракционную решетку, реализованную на массиве волноводов
(AWG).
7.3.1. Технология мультиплексирования на основе интерференционных
фильтров
178
Технология (де)мультиплексирования на основе интерференционных
фильтров - наиболее старая и распространенная, так как использует известные
принципы работы резонатора Фабри-Перо, состоящего из двух параллельных
зеркал и прозрачной непоглощающей диэлектрической среды между ними. Резонатор, как и любой интерференционный фильтр, настраивается на фильтрацию
одной длины волны. Он разделяет поток 1f,…1n на два потока: 1f и 12,…, 1n, выделяя несущую 3, из многоволнового потока, и для демультиплексирования л несущих необходимо установить каскадно п фильтров.
Аналогично резонатору FP работает и фильтр на многослойных диэлектрических тонких пленках. И в этом случае для демультиплексирования п несущих
необходимо установить каскадно n фильтров.
Обобщенная схема такого демультиплексора на 4 длины волны приведена
на рис.7.1. Из рисунка видно, что интерференционные фильтры (FP или DTF)
сформированы по обе стороны стеклянного блока (плоскопараллельной пластины, служащей для отражения не проходящего через фильтр потока) и снабжены специальными линзами для коллимации и фокусировки светового потока.
В данной конструкции для этой цели используются так называемые оптоволоконные GRIN-линзы. Нужно учитывать, что затухание таких фильтров на центральной частоте полосы пропускания достаточно велико, что делает целесообразным их использование в WDM с 8-16 каналами.
Другой принцип использован в фильтрах с циркулятором и отражательными ОВ-решетками Брэгга. Здесь отражение волны определенной длины происходит от дифракционной решетки Брэгга соответствующего периода, сформированной в одномодовом 0В. Отраженная волна, пришедшая на порт 2, транслируется циркулятором на порт 3 (рис. 7.2). Так как решетка Брэгга рассчитана на
фиксированную
179
Рисунок 7.1 – Схема демультиплексора WDM
на интерференционных фильтрах
длину волны, то для демультиплексирования несущих необходимо сформировать каскад из n отражательных решеток Брэгга, настроенных на соответствующие длины волн. Схема такого демультиплексора на 4 длины волны и приведена на рис. 7.2.
180
Рисунок 7.2 – Схеме демультиплексора WDM но основе
отражательной решетки Брэгга
7.3.2. Технология мультиплексирования на основе явления угловой дисперсии
Эта технология использует совершенно другие физические принципы.
Здесь входной коллимированный пучок падает на диспергирующий элемент и
пространственно разделяется им на несколько пучков, в зависимости от длины
волны несущей. Эти пучки, расходящиеся под различными углами, фокусируются и собираются отдельными приемными оптическими элементами. На выходе (в фокальной плоскости) этих элементов формируются изображения входного пучка, размеры которых (с помощью микролинзовых систем) юстируются
так, чтобы они соответствовали диаметру сердцевины приемного (выходного)
0В. Существует ряд проблем в получении нужного четкого изображения выходного пучка.
В качестве диспергирующих элементов могут быть использованы: •
призмы, как проходные, так и отражательные (причем схема Литтроу (Littrow)
более предпочтительна, так как позволяет использовать один комплект линз и
уменьшить габариты устройств, см. рис. 7.3;
181
Рисунок 7.3 – Схема демультиплексора WDM
на отражательной призме по теме Литтроу
• дифракционные решетки (плоская, отражательного типа) как с разделением входного и выходного пучков, так и с их совмещением (вновь используется
схема Литтроу, рис. 7.4). Дифракционные решетки нашли наиболее широкое
применение в качестве демультиплексоров WDM такого типа. Устройства, основанные на них, можно разделить по конструкции на две категории:
• плоские линейные решетки с отдельными фокусирующими элементами;
• самофокусирующиеся системы с решетками.
Наиболее удачной конструкцией первого типа можно считать цилиндрическую GRIN-линзус наклонной плоской дифракционной ре-
182
Рисунок 7.4 – Схема демультиплексора WDM
на отражательной плоской решетке по схеме Литтроу
шеткой (на стороне, противоположной входу, см. рис. 7.4). В числе конструкций
второго типа можно отметить ряд удачных (все используют схему Литтроу),
среди которых:
• а) схема, использующая для самофокусировки двояковогнутую (в двух
перпендикулярных плоскостях) дифракционную решетку;
• б) схема, использующая для самофокусировки вогнутую (в одной плоскости) цилиндрическую дифракционную решетку и пленарные волноводы;
• в) схема, использующая для коллимирования и самофокусировки вогнутое зеркало» плоскую дифракционную решетку (далее -как схема 300).
Названные три технологии, были разработаны еще в 80-х годах. Из них
схема (а) из-за сложности в реализации не нашла применения; схема (б) была
доработана и известна в настоящее время как схема с вогнутой дифракционной
решеткой- CG (Concave Grating); схема в) оказалась значительно более технологичной и известна в настоящее время как схема трехмерного (объемного) оптического мультиплексирования - 3DO (3-D Optics WDM). Мы рассмотрим более
подробно последнюю из них как наиболее перспективную.
7.4 Технология самофокусировки с вогнутым зеркалом и плоской решеткой
Эта технология, названная в работе технологией трехмерного оптического
мультиплексирования, использует классическую схему самофокусировки (рис.
7.5) с плоской отражательной дифракционной решеткой, вогнутым зеркалом (С)
и массивом волоконных световодов (0В), размещенных в пазах физической решетки с фиксированным шагом.
183
Рисунок 7.5 – Схема WDM (3DO) но основе трехмерного оптического
мультиплексирования:
а) оптически схема мультиплексирование 6) конструкции мультиплексора
Схема ее работы (в режиме демультиплексора) достаточно проста (рис. 7.5,
а). Мультиплексированный поток из входного волокна А, расходясь конусом с
углом Ь, отражается от зеркала и падает на дифракционную решетку, отражающую под разными углами свет разной длины волны. Эти дифрагированные лучи,
отражаясь от зеркала, фокусируются в определенных точках, где должны быть
расположены приемные порты массива волокон, выделяющих соответствующие
несущие. Для примера показано выделение одной такой несущей, конус лучей
которой (с тем же углом Ь) фокусируется в точке В (срез волокна выходного
порта).
Все элементы конструкции строго фиксированы в монолитном кварцевом
блоке (рис. 7.5, 6), что позволяет выдерживать и сохранять высокую точность
изготовления. Указанная конструкция может быть использована как с параболическим, так и сферическим зеркалами и имеет коэффициент увеличения, равный
1. Она афокальна (т.е. не имеет фокуса), так что все исходящие и входящие в
184
волокна углы одинаковы. Одномодовые волокна укладываются в канавки специальной физической решетки. Конструкция мультиплексора дает возможность использовать в решетке до 131 канавки (канала), что позволяет реализовать оптический шаг <1 нм, или до 262 каналов с шагом <0,5 нм.
7.4.1. Технология, использующая оптоволоконные направленные разветвители
Несмотря на значительные достижения в области технологии мультиплексирования на основе объемных микрооптических устройств, общая тенденция
развития волоконно-оптических систем передачи (ВОСП) и отдельных ее
устройств (в первую очередь мультиплексоров плотных и высокоплотных WDM)
состоит в совершенствовании пленарных технологий, которые органично сочетались бы с технологиями, используемыми при создании оптических интегральных схем (ОИС).
Наиболее простым и легко реализуемым в области пленарных технологий
вариантом мультиплексора WDM является мультиплексор на оптоволоконных
направленных разветвителях (ОВНР), схема которого приведена рис. 6. Она построена путем каскадного соединения однотипных ячеек разветвителей типа 2:1
(два входа - один выход), дающего в итоге мультиплексор n:1.
Рисунок 7.6 – Схема мультиплексора WDM на ОВНР
Такой метод построения схемы имеет очевидный недостаток -высокий
уровень вносимых потерь (теоретически 3 дБ/каскад). Его можно, конечно, компенсировать высоким уровнем входных оптических сигналов и установкой на
выходе оптического усилителя, но такое решение годится только для мультиплексора, но непригодно для демультиплексора, входные уровни сигналов которого малы.
7.4.2. Технология, использующая интерферометры Маха-Цендера
185
Развитием этого решения является использование интерферометров МахаЦендера (MZI), см. рис. 7.7, для демультиплексоров вместо разветвителей.
Структура демультиплексора построена по схеме бинарного дерева, а значит, она
может быть использована для систем WDM с числом несущих, равных величине
2 n.
Рисунок 7.7 – Схема демультиплексора WDM
на интерферометрах Маха-Цендера
Явное преимущество этого решения - планарность схем MZI и простота
его реализации в виде ОИС.
7.4.3. Технология, использующая дифракционную решетку на массиве
волноводов
Принципы, используемые в двух предыдущих решениях, были логически
объединены в технологии, основанной на формировании дифракционной решетки на массиве волноводов - AWG (Arrayed Waveguide Grating).
В основе технологии AWG (рис. 7.8, а) лежит обобщенный принцип интерферометра Маха-Цендера. Мультиплексор AWG состоит из двух многопортовых
разветвителей (входного и выходного), соединенных массивом пленарных оптических волноводов (МПОВ).
Длина каждого волновода Li отличается от соседних на фиксированную
величину D L, т.е. Li, = Li + D L, Li+1 = Li + D L Следовательно, каждую пару
волноводов вместе с входным и выходным разветвителями можно рассматривать
как интерферометр Маха-Цендера, a AWG в целом - как обобщенный интерферометр Маха-Цендера, т.е. устройство, генерирующее п копий входного сигнала
(с помощью входного разветвителя), распространяющихся в одинаковых средах
186
различной длины, и складывающее эти сигналы, пришедшие с разными фазовыми сдвигами, на выходе (с помощью выходного разветвителя).
AWG может использоваться как мультиплексор (n:1), осуществляющий
объединение п входных сигналов с группы входных портов 1 i1, 1i2,…, 1in в один
выходной – 10, или демультиплексор (1:п), осуществляющий разбиение входного
потока 10=SL, (i=1,2,... п) на отдельные несущие 101, 102,…, 10n и подачу их на
группу выходных портов n.
Схему AWG, конечно, можно было бы реализовать с помощью соединения
n/2 MZI, однако ее проще было бы сделать в виде планарной схемы с помощью
интегральных оптических технологий, так как входной и выходной разветвители
и массив волноводов можно реализовать на одной кремниевой подложке. Волноводы реализуются в виде пленарных оптоволоконных световодов (диоксид
кремния, легированный Ge или Та), сформированных на этой же подложке.
Многоканальные AWG (16-64 канала) выпускаются в виде готовых модулей, отличающихся малыми габаритами и средним уровнем вносимых потерь
(см. таблицу). Их температурный коэффициент достаточно высок (0,01 нм/°С),
что требует использования стабилизаторов температуры.
7.5 Принцип работы мультиплексора AWG
Допустим, что мультиплексор AWG имеет входной п • m и выходной m·n
разветвители, соединенные массивом из m световодов, длина которых отличается на D L, т.е. Li+1 = Li + D L. Входной разветвитель расщепляет сигнал с любого входного порта i на m входов массива световодов, предположим, что это
будет световод k. Пусть далее выходной разветвитель соединяет любой из m выходов массива световодов с выходным портом j. Тогда общий путь,
187
Волноводы
входные / выходные
λ1,λ2,...λn
Пластины
а)
SiO2
Полуволновая
пластина
188
Волновая матрица
λn
λ2
λ1
Рисунок 7.8 – Схема мультиплексирования WDM но основе дифракционной решетки на массиве волноводов: а) схема мультиплексора с входным и выходным разветвителями: 6) конструкции входного разветвителя по схеме с кругом Роуленда: в) схема мультиплексора с одним разветвителем И отражающим
зеркалом
проходимый светом от порта i до порта j через световод k, равен Dikj = (dik, + Lk+
dki). Длина Lk = L1 + (k-1) DL, где L1 - длина минимального (первого) световода.
Пусть, аналогично, длина dik = d1 + (k-1) ƌ di, a dki = dj + (k-1) ƌ dh где di и dj
- минимальные пути между входными/выходными портами разветвителей и входами/выходами световодов. Тогда относительные фазы сигналов, проходящих от
порта i до порта j через любой световод k=1,2.....т, составят:
(7.1)
Здесь n2 и n1 - коэффициенты преломления материала световодов (n2) и
входного и выходного разветвителей (n1).
Первое слагаемое в этой формуле постоянно, второе - показывает изменение относительной фазы ƌJikg. Те из волн, проходящих по пути Dikg, для которых
189
{n1 (ƌdi + ƌdj) + n2DL = p1, будут складываться в фазе на выходе j, а следовательно, несущая 1 будет выделена (демультиплексирована). Выполнение указанного условия возможно (но для другого 1), если заменить р на p+1, т.е. будет выделяться 1 и т. д. Это говорит о том, что, во-первых, АВХ мультиплексора AWG
имеет периодическую, гребенчатую, форму и, во-вторых, все длины волн системы WDM лежат в соответствующем свободном спектральном диапазоне FSR.
Указанные свойства напоминают интерферометрический фильтр на резонаторе Фабри-Перо, а физические принципы работы говорят о том, что массив
световодов, длина каждого из которых отличается от длин соседних световодов
на DL, играет роль дифракционной решетки, что делает понятным его название
- мультиплексор на основе дифракционной решетки на массиве волноводов.
Для понимания работы этого широко используемого типа мультиплексоров WDM интересно сделать ряд замечаний, касающихся некоторых деталей
конструкции мультиплексора, играющих важную роль в выполнении условий
фильтрации (сложения в фазе компонентов сигнала на выходе), поясняемых рис.
7.8, 6, а именно:
• входы массива световодов (выходные порты входного разветвителя) лежат на окружности решетки волноводов (ОРВ) радиуса R с центром в точке
входа центрального входного волновода;
• входы других входных волноводов лежат на окружности (вписанной в
ОРВ между ее центром и точкой касания общей касательной) диаметра R, эта
окружность называется кругом Роуленда,
• шаг распределения входных 0В и массива световодов постоянен в
направлении касательных в точках, между которыми вписан круг Роуленда;
• длина дуги ОРВ, занимаемая входами массива световодов, должна быть
много меньше R;
• при соблюдении вышеперечисленных условий длина пути между любым входом входного разветвителя и его любыми двумя последовательными выходными портами постоянна, а диапазон FSR примерно постоянен и не зависит
от выбора пары вход-выход (i-j) мультиплексора.
Для сокращения размеров мультиплексора вдвое и экономии компонентов
можно использовать схему Литтроу для компоновки мультиплексора, разрезав
его исходную схему (см. рис. 7.8, а) пополам и поместив в плоскости разреза
зеркало (см. рис. 7.8, в). Потоки несущих с выхода массива световодов будут отражаться зеркалом и подаваться со стороны внутренних выходных портов единственного разветвителя в тот же световод разветвителя, где будет происходить
интерференция входных и отраженных волн. Входной порт должен размещаться
при этом в центральном входном порту разветвителя.
Мультиплексор AWG может быть использован и в схемах с ин- терливингом. В этом случае, применяя однородную интегральную основу, можно создавать мультиплексоры AWG с удвоенным числом каналов. Число его обслуживаемых каналов - 102. Мультиплексор, построенный по схеме с использованием
интерливера, разделяющего входные 102 канала (частотного плана с шагом 50
ГГц) на два канала (с четными и нечетными несущими), в каждом из которых
190
используется мультиплексор AWG, рассчитан на обработку 51 канала частотного плана с шагом 100 ГГц.
7.6 Сравнение технологий оптического мультиплексирования
Во всех указанных решениях процедура мультиплексирования предполагается обратной по отношению к рассмотренной процедуре демультиплексирования. Параметры мультиплексоров WDM, реализованных на основе трех современных технологий, сведены в таблицу.
Из приведенных в таблице данных видно, что технология 3DO (3-D Optics)
WDM имела преимущество по четырем из пяти параметров и могла быть использована в системах WDM до уровня HDWDM с шагом несущих не меньше, чем
0,4 нм, и рассматриваться как перспективная. Однако новая генерация мультиплексоров AWG, используемая совместное интерливерами на основе AWG, дает
основание утверждать, как видно из строки "AWG (новая)", что наиболее перспективным и с точки зрения возможности увеличения числа каналов, и возможности использования современных интегральных технологий, является мультиплексор AWG.
Технология
ЧувствиМаксималь- Шаг между
Переходное
Вносимые
тельность к
ное число несущими,
затухание,
потери, дБ
поляризанесущих
нм
ДБ
ции, %
Температурный коэффициент,
нм/ْºС
AWG (старая) 32-64
0,8-15
6-8
-5— -29
2
0,01
AWG (новая)
102-400
0,2-0,8
2,2-6,4
-20—-33
0,3
н/д
CG
78
1-4
10-16
-7—-30
2-50
н/д
3D0
262
0,4-250
2-6
-30—-55
0
н/д
Кроме рассмотренного выше решения с использованием интерливера для
удвоения числа обрабатываемых каналов, которое, вообще говоря, применимо к
любому типу мультиплексора, есть пример мультиплексора AWG на 256 каналов
для частотной сетки с шагом 25 ГГц (который при использовании решения с интерливером может, в принципе, обрабатывать 512 каналов). Этот мультиплексор
имеет эквивалентную ширину полосы канального фильтра 0,12 нм на уровне ЗдБ с уровнем переходной помехи порядка -33 дБ и вносимыми потерями на
уровне 4,4 дБ для центральных портов и 6,4 дБ для периферийных портов.
Группа исследователей сообщила также о разработке аналогичного мультиплексора, но на 400 каналов для частотной сетки с шагом 25 ГГц, покрывающего диапазон 1530-1610 нм. Он обеспечивает уровень вносимых потерь от 3,8 дБ (в центре) до 6,4 дБ (на периферии).
191
192
ЗАКЛЮЧЕНИЕ
В пособии рассмотрены основные компоненты, которые применяются в
системах оптической связи. Приведены физические принципы функционирования компонентов ВОСП, даны технические и эксплуатационные параметры элементной базы.
193
ЛИТЕРАТУРА
1 Волоконно-оптические системы передачи: Учеб. для вузов/ М.М. Бутусов, С.М. Верник, С.Л. Галкин; Под ред. В. Н. Гомзина. – М.: Радио и связь, 1992.
2 Оптические системы передачи. Учеб. для вузов/ Под ред. Иванова В.И.М.: Радио и связь, 1994.
3 Фриман Р. Волоконно-оптические системы связи. – М.: Техносфера,
2003.
4 Волоконно-оптические системы передачи и кабели: Справ./ И.И. Гроднев, А.Г. Мурадян, Р.М. Шарафутдинов. - М.: Радио и связь, 1993.
5 Иванов А.Б. Волоконная оптика: компоненты, системы передачи, измерения. – М.: Сайрус системс, 1999.
6 Скляров О.К. Современные волоконно-оптические системы передачи.
Аппаратура и элементы. - М., 2001.
7 Волоконно-оптическая техника: история, достижения, перспективы/
Под. ред. Дмитриева С.А., Слепова Н.Н. – М., 2000.
8 Стерлинг Д. Дж. Техническое руководство по волновой оптике: Пер. с
англ. – М.: Лори, 2001.
9 Вербовецкий А.А. Основы проектирования цифровых оптоэлектронных
систем связи. – М.: Радио и связь, 2000.
10 Фокин В.Г. Современные оптические системы передачи информации. Екатеринбург: Изд-во УрТИСИ СибГУТИ, 2004.
11 Фокин В.Г. Волоконно-оптические системы передачи с подвесными кабелями на воздушных линиях электропередачи и контактной сети железных дорог: Метод. указ. – Новосибирск: Изд-во СибГУТИ, 2000.
12 Пихтин А.Н. Оптическая и квантовая электроника: Учеб. для вузов/А.Н.
Пихтин. – М.: Высш шк., 2001.
13 Бейли Д., Райт Э. Волоконная оптика. Теория и практика: Пер. с англ. –
М., 2006.
14 Лапина Н.Ф., Татаркина О.А. Волоконно-оптические системы передачи:
Методические указания к выполнению лабораторных работ для специальности
201000 "Многоканальные телекоммуникационные системы" - Екатеринбург:
Изд-во УрТИСИ ГОУ ВПО "СибГУТИ", 2004
15 Журналы "Электросвязь", "Вестник связи" и др.
16 ГОСТ 26599-85 Системы передачи волоконно-оптические. Термины и
определения
17 ГОСТ 2.761-84: ЕСКД. Обозначения условные графические в схемах.
Компоненты волоконно-оптических систем передачи
18 Рекомендации ITU-T G.694.1 (06/2002) Специальные решетки для спектрального разделения. Решетка DWDM (плотного спектрального мультиплексирования по длине волны DWDM) / Международный Союз Электросвязи. – Женева, 2002. – 14 с.
194
19 Рекомендации ITU-T G.694.2 (12/2003) Специальные решетки для спектрального разделения. Решетка CWDM (разреженного спектрального мультиплексирования по длине волны) / Международный Союз Электросвязи. – Женева, 2004. – 12 с.
195
Оглавление
СОКРАЩЕНИЯ И ОПРЕДЕЛЕНИЯ ........................................................................................... 4
1 ВОПРОСЫ ПОСТРОЕНИЯ ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ ПЕРЕДАЧИ .. 6
1.1 Основные эффекты и законы теории света ...................................................................... 6
1.2 Распространение световых лучей в оптических волокнах ........................................... 9
1.3 Типовая конструкция оптического волокна .................................................................. 11
1.4 Основы лучевой теории распространения света в ОВ ................................................. 14
1.5 Апертура оптического волокна ......................................................................................... 16
1.6 Затухание в волоконных световодах ................................................................................ 18
1.7 Дисперсия оптического волокна ....................................................................................... 20
1.8 Типичные характеристики волокон ................................................................................ 26
1.9 Кабели из оптических волокон ......................................................................................... 27
2 ИСТОЧНИКИ ОПТИЧЕСКОГО ИЗЛУЧЕНИЯ И УСИЛИТЕЛИ СВЕТА ............................. 33
2.1 Основные элементы оптического квантового генератора и оптического усилителя
2.2 Требования к источникам излучения .............................................................................. 36
2.3 Характеристики полупроводниковых материалов ...................................................... 36
2.4 Светодиоды ........................................................................................................................... 42
2.5 Резонаторы лазеров ............................................................................................................. 44
2.6 Оптические усилители ........................................................................................................ 52
2.7 Полупроводниковые лазеры .............................................................................................. 57
2.8 Соединение источников с волокном ................................................................................ 71
3 КОМПОНЕНТЫ МОДУЛЯЦИИ ОПТИЧЕСКОГО ИЗЛУЧЕНИЯ ................................. 75
3.1 Модуляция оптического излучения ................................................................................. 75
3.2 Внешняя модуляция ............................................................................................................ 87
3.2.1 Акустооптический эффект. Эффект Франца–Келдыша .................................................. 88
3.2.2 Электрооптический эффект ............................................................................................... 94
3.3 Фазовая модуляция ................................................................................................................ 99
3.4 Модуляторы по интенсивности ......................................................................................... 100
3.5 Параметры, полоса и мощность модуляции ...................................................................... 104
3.6 Электроабсорбционные модуляторы ................................................................................. 106
4 КОМПОНЕНТЫ ДЕТЕКТИРОВАНИЯ ОПТИЧЕСКОГО ИЗЛУЧЕНИЯ ................... 109
4.1 P-i-n фотодетекторы............................................................................................................. 109
4.2 Принцип действия фотодиодов ....................................................................................... 109
4.3 Основные характеристики фотодиодов ........................................................................ 111
4.4 Лавинные фотодиоды ....................................................................................................... 114
4.5 Характеристика спектральной чувствительности ............................................................ 119
4.6 Быстродействие .................................................................................................................... 119
4.7 Темновой ток и шум лавинного умножения ..................................................................... 121
5 КОМПОНЕНТЫ ВОЛОКОННО-ОПТИЧЕСКИХ ТРАКТОВ ........................................ 126
5.1 Диэлектрический пленочный волновод ........................................................................ 126
5.2 Оптические волокна и кабели ......................................................................................... 132
5.3 Распространение света и межмодовая дисперсия в градиентных волокнах ......... 134
5.4 Затухание в волноводах .................................................................................................... 137
5.5 Дисперсионные искажения волоконно-оптического кабеля .................................... 137
5.6 Затухание в основных элементах волоконно-оптического тракта .......................... 140
6 ПАССИВНЫЕ КОМПОНЕНТЫ ВОЛОКОННО-ОПТИЧЕСКИХ СИСТЕМ ПЕРЕДАЧИ 142
6.1 Пассивные оптические элементы ................................................................................... 142
6.2 Основные определения ........................................................................................................ 143
6.3 Определение функциональных параметров ...................................................................... 144
6.4 Разъемные и неразъемные соединения .............................................................................. 149
6.5 Волоконно-оптические элементы ветвления потока (разветвители) .............................. 161
196
33
6.6 Оптические аттенюаторы .................................................................................................... 168
6.7 Изоляторы, их параметры ................................................................................................... 169
6.8 Волоконно-оптические фильтры ........................................................................................ 173
6.9 Элементы коммутации и коммутаторы ............................................................................. 173
7 КОМПОНЕНТЫ КОММУТАЦИИ И МУЛЬТИПЛЕКСИРОВАНИЯ ................................... 176
7.1 Введение ............................................................................................................................... 176
7.2 Элементы спектрального разделения оптических мультиплексоров ............................. 177
7.3 Технологии демультиплексирования систем WDM и DWDM........................................ 178
7.4 Технология самофокусировки с вогнутым зеркалом и плоской решеткой.................... 183
7.5 Принцип работы мультиплексора AWG............................................................................ 187
7.6 Сравнение технологий оптического мультиплексирования ............................................ 191
ЗАКЛЮЧЕНИЕ .............................................................................................................................. 193
ЛИТЕРАТУРА ................................................................................................................................ 194
197