В данном разделе рассмотрены математические ... стороннего ОМП по ПАР при однофазном, двухфазном и трехфазном ПОВРЕЖДЕНИЯ

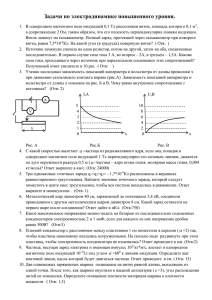
2 МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДЛЯ ОПРЕДЕЛЕНИЯ МЕСТА
ПОВРЕЖДЕНИЯ
В данном разделе рассмотрены математические модели одностороннего ОМП по ПАР при однофазном, двухфазном и трехфазном
КЗ на ВЛ напряжением 110 кВ. При составлении математических моделей учитывался ряд факторов, влияющих на точность ОМП. К этим
факторам относятся:
- переходное сопротивление в месте повреждения;
- система с противоположного замера конца линии;
- ответвления линии;
- магнитосвязанные линии.
2.1 Однофазное короткое замыкание
Рассмотрен общий случай однофазного КЗ через переходное сопротивление на двухцепной линии с ответвлением при двустороннем питании.
Под переходным сопротивлением Rп для данного вида КЗ будем понимать активное суммарное сопротивление дуги в месте повреждения и сопротивления земли. На рис.2.1 показана схема замещения поврежденной
фазы линии, представленная сосредоточенными параметрами, при однофазном КЗ через переходное сопротивление Rп за ответвлением. Где ЦР – цифровой регистратор, контролирующий параметры режима со стороны системы С1.
Уравнение, составленное по петле КЗ для поврежденной фазы [104],
согласно рис. 2.1 имеет следующий вид:
I ab ab
II ab ab
Uф  I1I ab  Z1ab  I I2ab  Zab
 ZM  I1I bc  Z1bc  I I2bc  Zbc
2  I 0  Z0  I 0
2 

I bc
II bc
 I0I bc  Z0bc  I0II bc  Zbc
 IC2
M  3  R П  I0  I0
0

, (2.1)
где I1I ab , I I2ab , I 0I ab , I1I bc , I I2bc , I 0I bc – токи прямой, обратной и нулевой
последовательностей поврежденной фазы линии №1 на участках
ab и bc соответственно;
ab
bc
bc
bc
Z1ab , Zab
2 , Z0 , Z1 , Z 2 , Z0 – сопротивления прямой, обратной
и нулевой последовательностей участков ab и bc;
I 0II ab , I 0II bc – токи нулевой последовательности параллельной ли-
нии (№2) на участках ab и bc;
49
Uф
ВЛ №2
С1
~
а
ВЛ №1
II
Z ab
I II ab
ф
ZI
ab
Z II
bd
bd
Zм
Z ab
м
b
С2
I II bc
ф
ZI
bc
ZI
cd
c
~
d
К(1)
50
ЦР
I I bc
ф
I ab
Iф
II отв
I0
I отв
I0
II bd  I C2
Iф
ф
Rп
I к 3  I 0Σ
Рис. 2.1 – Схема замещения двухцепной линии при КЗ за ответвлением
через переходное сопротивление Rп
50
bc
Z ab
M , Z M – взаимное сопротивление линий на участке ab и bc;
Rп – переходное сопротивление;
I C2
– ток нулевой последовательности тока КЗ от системы С2 с
0
противоположного замера конца линии.
Согласно классическому представлению однофазного КЗ на
землю [105] токи симметричных составляющих в месте КЗ связаны
следующим соотношением:
I1  I 2  I0 .
(2.2)
При допущении, что условие (2.2) распространяется на питающие КЗ ветви, выражение (2.1) примет вид


II ab ab
II bc
I bc
II bc
Uф  I0I ab  Zab
 ZM  I0I bc  Zbc
 Zbc
 IC2
Σ  I0
Σ  I0
M  3R П  I 0  I 0
0 ,
(2.3)
bc
где Zab
Σ , ZΣ – суммарные сопротивления прямой, обратной и нулевой
последовательностей участков ab и bc, определяемые как
bc
bc
bc
bc
ab
ab
ab
Zab
Σ  Z1  Z 2  Z0 , Z Σ  Z1  Z 2  Z0 .
В рассматриваемом общем случае равенство (2.2) выполняется
для подпитывающих ветвей только приближенно, из-за наличия токов
нагрузки. Для корректного описания в выражение (2.3) введем добавки
ΔI ф
 Z1ab  (I фI ab  3  I 0I ab )  Z1ab ;
I bc
ΔI ф
 Z1bc
I ab
(2.4)

(I фI bc
 3  I 0I bc )  Z1bc ,
которые будут учитывать реальное соотношение токов симметричных
составляющих. Окончательное уравнение по петле КЗ будет иметь вид
I bc
bc
II bc
Uф  Δ U1  I0I bc  Zbc
 Zbc
Σ  Δ Iф  Z1  I0
M  ΔUR ,
где Δ U1 – падение напряжение на участке ab определяемое как
51
(2.5)
Iab
ab
IIab
Δ U1  I0  ZΣ  I0
IIab ab
 Zab
M  Δ Iф  Z1 ;
(2.6)
Δ U R – падение напряжения на переходном сопротивлении:
ΔUR
 3  R  I0Ibc  I0IIbc  IC2
0   3  R П  I 0K .
(2.7)
Комплексное уравнение (2.5) содержит три неизвестные величины:
переходное сопротивление Rп, ток нулевой последовательности I C2
со
0
стороны системы С2 и сопротивление Zbc , определяемое расстоянием до
места повреждение. Учитывая, что комплексные числа считаются равными
между собой тогда и только тогда, когда в отдельности равны их вещественные и мнимые части [106], запишем комплексное уравнение (2.5) в
виде системы двух вещественных уравнений:




II bc
bc
I bc
bc
I bc
bc
 Im(I 0 )  x M  Re( ΔI ф )  r1  Im( ΔI ф )  x 1  


 ; (2.8)

 Re( ΔU R )


I bc
bc
I bc
bc
II bc
bc
Im(U ф )  Im( ΔU1 )  Re(I 0 )  x Σ  Im(I 0 )  rΣ  Re(I 0 )  x M  



II bc
bc
I bc
bc
I bc
bc
 Im(I 0 )  rM  Re( ΔI ф )  x 1  Im( ΔI ф )  r1  



 Im( ΔU R )


I bc
bc
I bc
bc
II bc
Re(U ф )  Re( ΔU1 )  Re(I 0 )  rΣ  Im(I 0 )  x Σ  Re(I 0
bc
)  rM 
где
II ab
ab
Re( ΔU1 )  Re(I 0I ab )  rΣab  Im(I 0I ab )  x ab
)  rM

Σ  Re(I 0
I ab
ab
I ab
ab
 Im(I 0II ab )  x ab
M  Re( ΔI ф )  r1  Im( ΔI ф )  x 1
52
I ab
ab
II ab
Im( ΔU1 )  Re(I 0I ab )  x ab
)  x ab
Σ  Im(I 0 )  rΣ  Re(I 0
M 
ab
 Im(I 0II ab )  rM
 Re( ΔI фI ab )  x1ab  Im( ΔI фI ab )  r1ab
В выражении (2.8) выразим все сопротивления посредством коэффициентов связи относительно X1bc следующим образом:
bc
bc
bc
rΣbc  K R  x1bc , x bc
Σ  K X  x1 , rM  K MR  x1 ,
bc
bc
bc
x bc
M  K MX  x1 , r1  K R1  x1 ,
откуда
KR 
2  r1bc  r0bc
x
bc
1
x 0bc , K  rMbc ,
x1bc MR x1bc
, KX  2 
K MX 
x bc
M ,
x1bc
K R1 
(2.9)
r1bc .
x1bc
Принимая во внимание равенство удельных сопротивлений участков bc
bd
и bd Zbc
уд  Z уд , выражения (2.9) примет вид
KR 
2  r1bd  r0bd
x
bd
1
, KX  2 
K MX 
x bd
M ,
x1bd
x 0bd , K  rMbd ,
x1bd MR x1bd
K R1 
(2.10)
r1bd .
x1bd
С учетом коэффициентов связи систему уравнений (2.10) запишем в
следующем виде:
53




II bc
II bc
 Re(I 0 )  K MR  Im(I 0 )  K MX  



I bc
I bc
bc
 Re( ΔI ф )  K R1  Im( ΔI ф )]  x1  



 Re( ΔU R )


.
I bc
I bc

Im(U ф )  Im( ΔU1 )  [Re(I 0 )  K X  Im(I 0 )  K R 



II bc
II bc
 Re(I 0 )  K MX  Im(I 0 )  K MR  


I bc
I bc
bc 
 Re( ΔI ф )  Im( ΔI ф )  K R1 ]  x 1  



 Im( ΔU R )


I bc
I bc
Re(U ф )  Re( ΔU1 )  [Re(I 0 )  K R  Im(I 0 )  K X 
(2.11)
Учитывая выражение (2.7), выразим в уравнениях системы (2.11) величину Rп:

Re(U ф)  Re( ΔU1 )  Re(I Σ )  x 1bc
 3 Rп 
Re(I 0K )

,


Im(U ф)  Im( ΔU1 )  Im(I Σ )  x 1bc
 3 Rп 

Im(I 0K )

(2.12)
где
Re(I  )  Re(I
I bc
0 )  KR
 Im(I
I bc
0 )  KX
 Re(I
II bc
0 )  K MR

;
 Im(I
II bc
0 )  K MX
 Re( ΔI
54
I bc
ф )  K R1
 Im( ΔI
I bc
ф )
Im(I  )  Re(I
I bc
0 )  KX
 Im(I
I bc
0 )  KR
 Re(I
II bc
0 )  K MX

;
 Im(I
II bc
0 )  K MR
 Re( ΔI
I bc
ф )
Im( ΔI
I bc
ф )  K R1
Re( I0K )  Re( I 0I bc )  Re( I 0II bc )  Re( I C2
0 );
Im(I 0K )  Im(I 0I bc )  Im(I 0II bc )  Im(I C2
0 ).
Полученная система уравнений (2.12) позволяет исключить неизвестную величину Rп:
Re(U ф)  Re( ΔU1 )  Re(I Σ )  x1bc Im(U ф)  Im( ΔU1 )  Im(I Σ )  x1bc
.

Re(I 0K )
Im(I 0K )
(2.13)
Решение уравнения (2.13) относительно величины X1bc имеет следующий вид:
x1bc
Re( Uф)  Re( Δ U1 )  [Im( Uф)  Im( Δ U1 )] 

Re( I Σ )  Im( I Σ ) 
Re( I 0K )
Re( I 0K )
Im( I 0K ) .
(2.14)
Im( I 0K )
Полученное выражение имеет две неизвестные величины: искомое сопротивление X1bc и ток I C2
0 от системы С2 в составе тока I 0K .
Представим (2.14) в следующем виде:
x1bc  Re( Uф)  Re( Δ U1)  [Im( Uф)  Im( Δ U1)]  ctgφ R
Re( I Σ )  Im( I Σ )  ctgφ R
,
(2.15)
где
ctgφ R 
Re( I0K )
Im( I0K )

Re( I0I bc )  Re( I0II bc )  Re( IC2
0 )
Im( I0I bc )  Im( I0II bc )  Im( IC2
0 )
55
.
(2.16)
Так как токи КЗ в сети одной ступени напряжения близки по
фазе (для сети 110 кВ примерно 70˚), то можно сделать допущение, что
неучет тока I C2
от системы С2 при замере с одной стороны не внесет
0
существенной погрешности в определении реактивного сопротивления
искомого участка линии x 1bc по формуле (2.15). Следовательно, выражение (2.15) полностью определено при замере с одной стороны и допущении, что
ctgφ R 
Re( I 0I bc )  Re( I 0II bc )
Im( I 0I bc )  Im( I 0II bc )
.
(2.17)
На основании вышеприведенных выкладок можно предложить
расчетную формулу для определения расстояния до места повреждения
при однофазном КЗ по ПАР одного из питающих концов линии в сети
с эффективно заземленной нейтралью:
 при однофазном КЗ на двухцепной линии за ответвлением
(рис.2.1):
L X  Lab 

Re(U ф)  Re( ΔU1 )  [Im(U ф)  Im( ΔU1 )]  ctgφ R

Re(I Σ )  Im(I Σ )  ctgφ R
, (2.18)
1
x1bdуд.
где L X – искомое расстояние;
Lab – длина участка линии до ответвления;
Uф – напряжения поврежденной особой фазы;
x1bdуд.

– удельное реактивное сопротивление прямой последова-
тельности участка bd поврежденной линии.
при однофазном КЗ на двухцепной линии перед ответвлением:
LX 
где
x1abуд.
Re( Uф)  Im( Uф)  ctgφ R

Re( IΣ )  Im( I Σ )  ctgφ R
1
x1abуд.
,
(2.19)
– удельное реактивное сопротивление прямой последова-
тельности участка ab поврежденной линии;
56
Re(I  )  Re(I 0I ab )  K R  Im(I 0I ab )  K X  Re(I 0II ab )  K MR 
;
 Im(I
II ab
)  K MX
0
 Re( ΔI фI ab )  K R1
 Im( ΔI фI ab )
Im(I  )  Re(I 0I ab )  K X  Im(I 0I ab )  K R  Re(I 0II ab )  K MX 
;
 Im(I
II ab
)  K MR
0
 Re( ΔI фI ab )  Im( ΔI фI ab )  K R1
I ab
I ab
Re(ΔIф
)  Re(Iф
)  Re(3 I0I ab ) ;
I ab
I ab
Im(ΔIф
)  Im(Iф
)  Im(3 I0I ab ) ;
KR 
2  r1ab  r0ab
K MR 

x1ab
rMab ;
x1ab
; KX  2 
K MX 
x ab
M ;
x1ab
x ab
0
;
x1ab
K R1 
r1ab .
x1ab
при однофазном КЗ на одноцепной линии за ответвлением
(рис.2.2) расчетное выражение аналогично выражению (2.19), но
без составляющих, учитывающих наличие магнитосвязанной линии:
ab
ab
ab
ab
ab
ab
ab
Re(U1)  Re(Iab
0 )  rΣ  Im(I0 )  x Σ  Re(ΔIф )  r1  Im(ΔIф )  x1 ;
ab
ab
ab
ab
ab
ab
ab
Im(U1)  Re(Iab
0 )  x Σ  Im(I0 )  rΣ  Re(ΔIф )  x1  Im(ΔIф )  r1 ;
bc
bc
Re(I )  Re(I0bc )  K R  Im(I0bc )  K X  Re(ΔIф
)  K R1  Im(ΔIф
) ;
bc
bc
Im(I )  Re(I0bc )  K X  Im(I0bc )  K R  Re(ΔIф
)  Im(ΔIф
)  K R1 .
57
U
С1
ф
а
Z
ab
b
Z
bc
~
Z
c
К(1)
58
ЦР
I ab
ф
bc
IIbc
фф
Rп
I отв
0
cd
I C2
ф
I к  3  I 0Σ
Рис. 2.2 – Схема замещения одноцепной линии при КЗ за ответвлением
через переходное сопротивление Rп
58
d
С
2
~

при однофазном КЗ на одноцепной линии перед ответвлением расчетное выражение аналогично выражению (2.18), но без составляющих, учитывающих наличие магнитосвязанной линии:
ab
ab
ba
Re( I )  Re( Iab
0 )  K R  Im( I0 )  K X  Re( Δ Iф )  K R1  Im( Δ Iф ) ;
ab
ab
ab
Im( I )  Re( Iab
0 )  K X  Im( I0 )  K R  Re( Δ Iф )  Im( Δ Iф )  K R1 .
Учет влияния ответвления. Использование регистратора на
одном из концов линии (рис.2.1), т.е. при одностороннем измерении
позволяет иметь информацию о ПАР только в месте замера. Наличие
ответвления на поврежденной линии при КЗ за ответвлением изменяет
потокораспределение вдоль всей линии. Это приводит к появлению
дополнительной неизвестной величены в выражении (2.14). Этой велиI bc
чиной является Iф
– ток поврежденной линии после ответвления.
I ab
I bc
Разница токов в месте замера Iф
и тока после ответвления Iф
определяется током ответвления:
I ab
I bс
I отв
.
Iф
 Iф
 Iф
(2.20)
При учете ответвления прежде всего следует отметить тот факт,
что на ток ответвления влияет режим работы трансформаторов ответвления. Наличие заземленных нейтралей трансформаторов ответвления
приводит к появлению тока нулевой последовательности ответвления,
который прежде всего и определяет полный ток ответвления при однофазном КЗ. Поэтому рассмотрим сначала учет тока нулевой последовательности ответвления.
Ток нулевой последовательности ответвления будет иметь место
только в случае заземленных нейтралей трансформаторов ответвления
при КЗ связанных с землей. Так как нас интересует однофазное КЗ за
ответвлением, то рассмотрим схему замещения нулевой последовательности поврежденной фазы двухцепной линии с ответвлением при
заземленном режиме работы нейтралей трансформаторов ответвления,
изображенную на рис.2.3.
59
U0
ВЛ №2
С
~1
а ВЛ №1
Z 0II bd
Z 0II ab
I 0II ab
Z 0I ab
Z
ab
м
Z
b
I 0I ab
60
ЦР
bd
м
I
II отв
0
Z
I
отв
м
Z ab
м
Z 0I cd d
Z 0I bc c
I 0I bc
С2
II bd
0
К(1)
I 0II bd  I C2
0
I 0I отв
Z0лин II
Z0линI
Z0тр I
Z0тр II
Рис. 2.3 – Схема замещения нулевой последовательности двухцепной линии с ответвлением
при КЗ за ответвлением
60
~
Согласно схеме замещения напряжение нулевой последовательности в месте подключения ответвления равно
U 0I отв  U 0I  Δ U 0I ab ,
(2.21)
U 0II отв

U 0II  Δ U 0II ab ,
где U 0I и U 0II – напряжения нулевой последовательности линий I и II в
месте замера;
I ab
ΔU0
и
II ab
ΔU0
– падения напряжения нулевой последователь-
ности на участке ab линий I и II, определяемые следующими выражениями:
I ab
ΔU 0
II ab
 I 0I ab  Z ab
 Z ab
0  I0
M;
.
II ab
ΔU 0

I 0II ab

Z ab
0

I 0I ab

(2.22)
Z ab
M.
Токи нулевой последовательности найдем из уравнений, составленных для ответвления:
I отв
I0I отв  Z0I отв  I0II отв  Zотв
,
M  U0
(2.23)
II отв II отв
I0I отв  Zотв
 Z0
M  I0
  U 0II отв,
где Z 0I отв и Z0II отв – суммарное сопротивление нулевой последовательности ответвления I и II, состоящее из сопротивления нулевой
последовательности линии и сопротивления нулевой последовательности
трансформатора
[107]:
Z0I отв  Z0I лин  Z0I тр ;
Z0II отв  Z0II лин  Z0II тр ;
Zотв
M – сопротивление взаимоиндукции линий I и II ответвления.
С учетом (2.21) и (2.22) выражение (2.23) примет следующий
вид:
61
Δ U0
II ab
I отв
 I0I ab  Zab
 Zab
 Z0I отв  I0II отв  Zотв
0  I0
M   I0
M ;
II
Δ U0
 I0I ab
I
(2.24)
 Zab
0
 I0II ab
 Zab
M

I0I отв  Zотв
M
 I0II отв  Z0II отв .
Решение уравнения (2.24) дает значение токов нулевой последовательности ответвления:
 U 0I отв
I0I отв 
 U 0II отв
Z0I отв
Zотв
M
Z0II отв
Zотв
M
Zотв
M
Z0II отв
Z0I отв
Zотв
M
Z0I отв
Zотв
M
 U 0I отв
 U 0II отв
Zотв
M
Z0II отв
;
(2.25)
I0II отв 
.
Рассмотрим учет токов прямой и обратной последовательностей
ответвления. Токи прямой и обратной последовательностей ответвления будут иметь место при любых режимах работы нейтралей трансформаторов ответвления, так как их путь протекания не связан с землей. Их точный расчет затруднен учетом реального сопротивления
нагрузки и возможной подпиткой от двигателей. При известных сопротивлениях нагрузки и неучете подпитки от двигателей токи прямой и
обратной последовательностей можно рассчитать по схеме, изображенной на рис.2.4. На рис.2.4 показана схема замещения прямой и обратной последовательностей поврежденной фазы линии с ответвлением при однофазном КЗ за ответвлением. Отличие от схемы замещения
нулевой последовательности заключается в отсутствии сопротивления
взаимосвязи между параллельными линиями. Поэтому схемы замещения прямой и обратной последовательностей для двухцепной линии не
имеет взаимных сопротивлений.
62
U 1(2)
С1
Z1I ab
а
b
Z 1I bc
Z 1I cd d
c
~
С2
~
К(1)
ЦР
I
I ab
1(2)
I bc
I 1(2)
C2
I 1(2)
Iл
Z 1(2)
63
Iт
Z 1(2)
I отв
I 1(2)
I нагр
Z 1(2)
Рис. 2.4 – Схема замещения прямой и обратной последовательностей линии
с ответвлением при КЗ за ответвлением
63
Аналогично нулевой последовательности напряжение прямой и
обратной последовательностей в месте подключения ответвления
(рис.2.4) равны
U 1I отв  U 1I  I1I ab  Z1I ab ;
(2.26)
U I2отв

U I2
 I I2ab
 Z I2ab ,
где U1I и U I2 – напряжения прямой и обратной последовательностей в
месте замера;
I1I ab и I I2ab – токи прямой и обратной последовательностей участ-
ка линии ab;
Z1I ab и ZI2ab – сопротивления прямой и обратной последователь-
ностей участка линии ab.
Из уравнений ответвлений
I1I отв  Z1I отв   U1I отв ;
(2.27)
I I2отв  ZI2отв

 U I2отв ,
где Z1I отв и Z I2отв – суммарные сопротивления прямой и обратной
последовательностей ответвления состоящих из соответствующих
сопротивлений
линии,
трансформатора
и
нагрузки:
I отв
 Z I2лли  Z I2тт  Z I2нагр ,
Z1I отв  Z1I лли  Z1I тт  Z1I нагр ; Z 2
найдем токи прямой и обратной последовательностей ответвления:
I1I отв 
 U1I отв
Z1I отв
;
(2.28)
I I2отв 
 U I2отв
Z2I отв
.
Полный ток ответвления в поврежденной фазе равен
64
I отв
Iф
 I1I отв  II2отв  I0I отв .
(2.29)
На основании сделанных выкладок в формулах (2.18) и (2.19) с
учетом тока ответвления будут иметь место следующие соотношения:
 в формуле (2.18):
I bc
I ab
I отв
Re( ΔIф
)  Re(I ф
)  Re(3  I0I ab )  Re(I ф
)  Re(3  I0I отв) 
;
I ab
I отв
 Re( ΔIф
)  Re( ΔIф
)
I bc
I ab
I отв
Im( ΔIф
)  Im(I ф
)  Im(3  I0I ab )  Im(I ф
)  Im(3  I0I отв) 
;

I ab
I отв
Im( ΔIф
)  Im( ΔIф
)
Re(I 0I bc )  Re(I 0I ab )  Re(I 0I отв) ; Im(I 0I bc )  Im(I 0I ab )  Im(I 0I отв) ;
Re(I 0II bc )  Re(I 0II ab )  Re(I 0II отв) ,
Im(I 0II bc )  Im(I 0II ab )  Im(I 0II отв) ;
I отв
I отв
где Δ Iф
 Iф
 3  I0I отв – добавка тока, учитывающая реальное
соотношение симметричных составляющих тока ответвления
(аналогично (2.4).
 в формуле (2.19):
I bc
I ab
I отв
Re( ΔIф
)  Re(I ф
)  Re(3  I0I ab )  Re(I ф
)  Re(3  I0I отв) 
;

I ab
I отв
Re( ΔIф
)  Re( ΔIф
)
65
I bc
I ab
I отв
Im( ΔIф
)  Im(I ф
)  Im(3  I0I ab )  Im(I ф
)  Im(3  I0I отв) 
;

I ab
I отв
Im( ΔIф
)  Im( ΔIф
)
Re(I 0I bc )  Re(I 0I ab )  Re(I 0I отв) , Im(I 0I bc )  Im(I 0I ab )  Im(I 0I отв) .
2.2 Двухфазное короткое замыкание
Рассмотрим случай двухфазного КЗ через переходное сопротивление между поврежденными фазами. Предположим, что КЗ произошло между фазами В и С. На рис.2.5 показана схема замещения для
поврежденных фаз линии при двухфазном КЗ через переходное сопротивление Rп.
Уравнение, составленное по петле КЗ для поврежденных фаз,
согласно рис. 2.5 имеет следующий вид
U B  U C  Ι B  ΙC  Ζ  Δ U R ,
(2.30)
где Δ U R – падение напряжения на переходном сопротивлении:
C1
C2
Δ U R  (I R  I R )  R п
.
(2.31)
Следует отметить, что ток нагрузки I НАГР (рис.2.5) не будет
проходить через переходное сопротивление, так как
C2
C2
C2
IC1
R  I R  I B  I C  I B  I C  ( I B1  I B2  I B НАГР )  ( IС1  I С2 
C2
C2
C2
C2
C2
 IС НАГР )  (IC2
B1  I B2  I B НАГР )  ( I С1  I С2  I С НАГР ) 
C2
C2
C2
 (I B1  I B2 )  (IС1  IС2 )  (IC2
B1   I B2 )  ( I С1  IС2 )
66
, (2.32)
IB  IB1  I B2  IB НАГР
UB
С1
IB  IB1  I B2  I B НАГР
Z
UB
С2
I
~
67
UC
ЦР
C1
R
Rп
I C2
R
Z
IС  IС1  IС2  IС НАГР
I С  I С1  I С2  I С НАГР
Рис. 2.5 – Схема замещения поврежденных фаз линии при двухфазном КЗ
67
~
C2
C2
C2
где I B1 , I B2 , I C1 , I C2 , I C2
B1 , I B2 , I C1 , I C2 – токи прямой и обратной по-
следовательности поврежденных фаз от системы С1 и системы С2
соответственно;
I B НАГР , I C НАГР – токи нагрузки поврежденных фаз.
Представим уравнение (2.30) в следующем виде:
U  Ι  Ζ  IR  R п ,
(2.33)
где U  U B  U C – разность напряжений поврежденных фаз;
I  I B  I C – разность токов поврежденных фаз;
C2
I R  IC1
R  I R – ток КЗ через переходное сопротивление.
В виде системы двух вещественных уравнений выражение (2.33) имеет
вид
Re( U)  Re( I)  r  Im( I)  x  Re( I R )  R п 
.

Im( U)  Re( I)  x  Im( I)  r  Im( I R )  R п 

(2.34)
Введем коэффициент связи
KR 
r,
x
(2.35)
тогда система (2.34) примет вид
Re(U)  Re(I)  K R  Im(I)  x  Re(I R )  R п 

.
Im(U)  Re(I)  Im(I)  K R  x  Im(I R )  R п 
(2.36)
Исключая величину Rп в уравнении (2.36), решим его относительно реактивного сопротивления искомого участка линии Х:
X
Re U   ImU   ctgφ R
,
Re I   (K R  ctgφR )  ImI   1  K R  ctgφR 
68
(2.37)
Re(I R )
– котангенс треугольника тока КЗ.
Im(I R )
В формуле (2.37) известны все составляющие, кроме величины
ctgφR , для которой информация определена недостаточно. Запишем
ctgφR с учетом (2.32) следующим образом:
где ctgφ R 
ctgφ R 
C2
Re(I B )  Re(I C )  Re(I C2
B )  Re(I C )
C2
Im(I B )  Im(I C )  Im(I C2
B )  Im(I C )
.
(2.38)
Согласно классическому представлению двухфазного КЗ [105]
ток в особой фазе (в нашем случае фазы А) в месте КЗ равен нулю
(рис.2.6):
I RА  I RА1  I RА2  0 .
(2.39)
Для токов двухфазного КЗ можно выполнить преобразование
выражения (2.38), учитывая соотношения между симметричными составляющими разных фаз (рис.2.6). При этом суммарный ток двухфазного КЗ равен
I R  (I R1B  I R2B )  (I R1C  I R2C )  2  3 I R2A(φ A2  90) .
(2.40)
С учетом (2.40) выражение (3.38) примет вид
I  cosφ R cos(φ A2  90  ) sinφ A2
ctgφ R  R


  tgφ A2 . (2.41)
I R  sinφ R
sin (φ A2  90  ) cosφ A2
Принимая во внимание (2.41), уравнение (2.37) можем записать следующим образом:
X
Re U   ImU   tgφ A2
,
Re I   (K R  tgφA2 )  ImI   K R  tgφA2  1
69
(2.42)
I R2B
I R2C
I R2C
+
I R1C  I R2C
I R1B  I R2B
70
φ A2
I R1C
I R1B
I R2A
+j
Рис. 2.6 – Симметричные составляющие токов через дугу при двухфазном КЗ
70
tgφ A2 
где
Im(I A2 )  Im(I C2
A2 )
Re(I A2 )  Re(I C2
A2 )
;
(2.43)
Re( I А2 ) , Im( I А2 ) – вещественная и мнимая составляющие тока
обратной последовательности особой фазы от системы С1;
С2
Re( I С2
А2 ) , Im( I А2 ) – вещественная и мнимая составляющие тока
обратной последовательности особой фазы от системы С2.
Если допустить, что I A2 и I C2
A2 имеют близкие по величине фаС2
зовые значения ( φ А2  φ А2 ) и учесть, что токи нагрузки не оказывают
влияния на расчет (2.32), формула (2.42) полностью определена при
замере с одной стороны в допущении, что:
tgφ А2 
Im( I А2 )
Re( I А2 )
.
(2.44)
На основании сделанных выкладок можно предложить расчетное выражение для определения расстояния до места повреждения при
двухфазном КЗ по ПАР одного из питающих концов линии в сетях с
эффективно заземленной нейтралью:
LX 

Re( U)  Im( U)  tgφ оф2




1
Re( I)  K R  tgφ оф2  Im( I)  K R  tgφ оф2  1 X УД
,
(2.45)
где L X – расстояние до места повреждения;
X УД – удельное реактивное сопротивление линии;
U – разность напряжений поврежденных фаз;
I – разность токов поврежденных фаз;
tgφоф2 – тангенс тока особой фазы;
K R – коэффициент связи.
2.3 Трехфазное короткое замыкание
Рассмотрим случай трехфазного КЗ через переходное сопротивление. Схема замещения фазы линии при трехфазном КЗ через пере71
ходное сопротивление показана на рис.2.7.
Уравнение, составленное по петле КЗ для одной фазы, имеет
следующий вид:


U Ф  IФ  Z  IФ  IC2
Ф  Rп ,
(2.46)
где U Ф – фазное напряжение в месте замера;
I Ф – фазный ток КЗ со стороны замера;
I C2
Ф – фазный ток КЗ от системы С2;
– сопротивление искомого участка линии;
Rп – переходное сопротивление.
Z
Уравнение (2.46) в виде системы двух вещественных уравнений
имеет вид
Re( U ф )  Re( I ф )  r  Im( I ф )  x  [Re( I ф )  Re( I фC2 )]  R п 


 , (2.47)

C2
Im( U ф )  Im( I ф )  x  Re( I ф )  r  [Im( I ф )  Im( I ф )]  R п 

где r и x – активное и реактивное сопротивления линии.
С коэффициентом связи
KR 
r
x
(2.48)
уравнение (2.47) можно записать следующим образом:
Re( U ф )  [Re( I ф )  K R  Im( I ф )]  x  Re( I K )]  R п 


,

Im( U ф )  [Im( I ф )  Re( I ф )  K R ]  x  Im( I K )]  R п 

(2.49)
где Re(I K )  Re(I ф )  Re(I фC2 ) ; Im(I K )  Im(I ф )  Im(I фC2 ) .
Решение уравнения (2.49) относительно реактивного сопротивления
искомого участка линии Х, можно представить в следующем виде:
72
С1
Uф
Iф
С2
Iф
С2
~
~
Z
ЦР
73
I
C1
ф
Rп
I
C2
ф
Рис. 2.7– Схема замещения фазы линии при трехфазном КЗ через переходное сопротивление
73
X
Re( UФ )  Im( UФ )  ctgφк
Re( IФ )  (K R  ctgφк )  Im( IФ )  (1  K R  ctgφк )
,
(2.50)
где
ctgφ K 
Re( I K )
Im( IK )

Re( IФ )  Re( IC2
Ф )
Im( IФ )  Im(IC2
Ф )
.
(2.51)
При допущении равенства фаз токов I Ф и I С2
Ф :
ctgφ K 
Re(I Ф )
.
Im(I Ф )
(2.52)
Принимая во внимание (2.52), преобразуем уравнение (2.50)
следующим образом:
X
Re(U Ф )  Im(U Ф ) 
Re(I Ф ) [K R 
Re(I Ф )
Im(I Ф )
Re(I Ф )
]  Im(I Ф ) [1  K R  Re(I Ф ) ]
Im(I Ф )
Im(I Ф )

(2.53)

Re(U Ф )  Im(I Ф )  Im(U Ф )  Re(I Ф )
(I Ф ) 2
.
Если выбрать вещественную ось, совпадающую по направлению
с U Ф , то уравнение (2.53) можно упростить:
U  sin α
,
X Ф
IФ
(2.54)
где α – аргумент тока I Ф .
Так как для индуктивной цепи α  φф , где
φф – угол между
напряжением и током одноименной фазы, выражение (2.54) примет вид
74
X
U Ф  sin φф
IФ
.
(2.55)
Расчетное выражение для определения расстояния до места
повреждения при трехфазном КЗ по ПАР одного из питающих концов
линии в сетях с эффективно заземленной нейтралью имеет вид
LX 
UФ  sinφф
IФ  X УД
,
(2.56)
где U Ф – модуль фазного напряжения;
I Ф – модуль фазного тока;
X УД – удельное реактивное сопротивление линии.
При замере с одной стороны целесообразно выполнять расчет
для каждой фазы, а расстояние до места повреждения брать как среднее арифметическое.
75