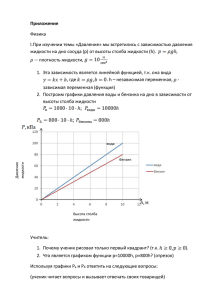
МБОУ СОШ № 6 Открытый урок по алгебре в 7 классе (урок систематизации и обобщения знаний и умений) Учитель: Лукьянова Людмила Анатольевна Цели и задачи урока: Образовательные: а) проверить и закрепить знания, умения и навыки учащихся по данной теме; б) научить применять знания на практике Развивающие: расширение кругозора, получение новых знаний: а) рассмотреть конкретные примеры линейных зависимостей, взятых из практики и смежных дисциплин. Воспитательные: а) повышение интереса к изучению математики б) воспитание трудолюбия, внимательности, аккуратности и ответственности при выполнении заданий в) содействие развитию самоконтроля, любознательности г) развитие коммуникативной культуры Технологии: проблемное обучение, обучение в сотрудничестве (групповая работа), ИКТ Оснащение урока: Ноутбук, мультимедийный проектор, экран, презентация, памятка – что должен знать учащийся по теме «линейная функция», раздаточный материал. Ход урока Организационный момент Приветствие учащихся, гостей. Проверка готовности учащихся к уроку. Учитель сообщает тему урока, акцентируя внимание учащихся на том, что они должны знать и уметь в результате изучения темы. Сообщает обучающую цель урока и план его проведения. I этап урока. Математический диктант (два варианта) Все задание показываются с помощью проектора и сопровождаются словесно учителем. 1) Даны пять функций. Выпишите те из них, которые являются линейными I вар. 𝑦 = 5 − 3𝑥 2 II вар. 𝑥 3 2 𝑦 =𝑥 −𝑥−1 𝑦=2+ 𝑦 = −3𝑥 4 𝑦 =− +3 𝑥 𝑦 = 5𝑥 𝑦=5 𝑥 𝑦 = −3 2 𝑦 = 5− 3 𝑥 𝑦 = −3 (2-3 мин на выполнение; 1 мин – на проверку) Ответ: I вар. 𝑦 = −3𝑥 II вар. 𝑦=5 𝑥 𝑦 = −3 2 𝑦=2+ 𝑥 3 𝑦 = 5𝑥 𝑦 = −3 Проверка осуществляется с помощью проектора, учащиеся ставят на листах у соответствующих функций «+» - верно, «-» - неверно. Контрольный вопрос: почему функции 𝑥 𝑥 2 3 а) − 3 (𝑦 = 2 + ); б) 𝑦 = 5 (𝑦 = −3) являются линейными. Указать 𝑘 и 𝑏. Ученики ставят себе оценку за выполнение 1-го задания 2) Построить графики выписанных линейных функций (8 мин – на выполнение, 2 мин – на проверку) Учитель показывает графики с помощью ММП. Анализируются ошибки. Ученики оценивают свою работу. I вар. y=-3x y=5 y=x/2-3 y=-3x y=5 y=x/2-3 II вар. y=5x y=2+x/3 y=-3 3) Выяснить, проходит ли график функции через заданную точку 𝑥 𝑦 = − 3, 𝐶(26; 8) 2 𝑥 𝑦 = 2 + , 𝑀(−42; −12) 3 3 мин – на выполнение, 1 мин – проверку Решение: 1 вар. х y С(26;8) 8= 8=13-3 26 −3 2 𝑥 8=10 – неверное числовое равенство, след. график функции 𝑦 = − 3 не 2 проходит через точку С. 2 вар. х y М(-42;-12) −12 = 2 + −42 3 −12=2-14 −12 = −12 - верное числовое равенство, след. график функции проходит через точку М. Учащиеся оценивают свою работу 4) Задать формулой функцию, график которой изображен на рисунке. I вар. II вар. 8 мин – на выполнение, 1 мин – на проверку Решение: 1 вар. 𝑦 = 𝑘𝑥 + 𝑏 1) b=3, 𝑦 = 𝑘𝑥 + 3 k>0 2) (-4;0) 0=k·(-4)+3 -3=k·(-4) 3 k= > 0 4 3 𝑦 = 𝑥 + 3. 4 2 вар. 𝑦 = 𝑘𝑥 + 𝑏 1) b=2 𝑦 = 𝑘𝑥 + 2 k<0 2) (5;0) 0=k·5+2 -2=k·5 2 k=− < 0 5 2 𝑦 = − 𝑥 + 2. 5 Учитель подводит итог математического диктанта. 1) Поднимите руку, пожалуйста, те, кто за все четыре задания поставил себе оценку а) «5», б) «5» и «4» Молодцы! 2) Тем, у кого есть «3» и «2» поработать над соответствующими вопросами данной темы, прийти на консультацию к учителю и затем сдать зачет. Листы с выполненными заданиями с/р ученики сдают учителю по колонкам, начиная с последних парт. II этап урока. Применение полученных знаний при решении практических задач. (17 мин) Учитель: рассмотрим конкретные примеры линейных зависимостей величин, взятые из смежных дисциплин. Учащиеся заранее были разбиты на группы: 1-ая – знакомилась с применением линейной зависимости в курсе физики 2-ая 3-я - знакомилась с применением линейной зависимости в курсе биологии 4-ая - на уроках трудового обучения От групп выделялись докладчики по данным вопросам. Слово предоставляется группе физиков. И т.д. По мере рассказов учащихся учитель соответствующие формулы зависимостей помещает в таблицу «Линейные зависимости величин в практике» (в кармашки) Физика – сообщение и вопросы к учащимся – 8 мин. Биология – сообщение – 3 мин Труд – сообщение и вопросы к учащимся – 3 мин. (См. Приложение) Приложение Физика I.При изучении темы «Давление» мы встретились с зависимостью давления жидкости на дно сосуда (p) от высоты столба жидкости (h). 𝑝 = 𝜌𝑔ℎ, 𝜌 − плотность жидкости, 𝑔 = 10 м сек2 1. Эта зависимость является линейной функцией, т.к. она вида 𝑦 = 𝑘𝑥 + 𝑏, где 𝑘 = 𝜌𝑔, 𝑏 = 0. h – независимая переменная, 𝜌 - зависимая переменная (функция) 2. Построим графики давления воды и бензина на дно в зависимости от высоты столба жидкости 𝑃в = 1000 · 10 · ℎ; 𝑃воды = 10000ℎ 𝑃б. = 800 · 10 · ℎ; 𝑃бензина = 800ℎ 𝑃, кПа вода Давление жидкости бензин вода бензин ℎ, м Высота столба жидкости Учитель: 1. Почему ученик рисовал только первый квадрант? (т.к. ℎ ≥ 0, 𝑝 ≥ 0). 2. Что является графиком функции p=10000h, p=800h? (отрезок) Используя графики Pв и Pб ответить на следующие вопросы: (ученик читает вопросы и вызывает отвечать своих товарищей) 1) Какое давление оказывает столб воды высотой 8 м? 2) При какой высоте столба бензина его давление на дно сосуда равно 40 кПа? 3) Что оказывает большее давление – бензин или вода при высоте столба жидкости 10 м? 4) Давление жидкости 70 кПа. Что больше – высота столба воды или высота столба бензина? на сколько? II. Сопротивление f дороги движению автомобиля при скорости движения v км/ч выражается следующими формулами: На асфальте 𝑓 = 14,5 + 0,25𝑣; 2 1 3 30 2 На хорошем шоссе 𝑓 = 24 − 𝑣 + 𝑣2; На булыжной мостовой 𝑓 = 29 − 𝑣 + 3 1 𝑣2; 16 3 1 4 30 На мягкой грунтовой дороге 𝑓 = 36,5 − 𝑣 + 𝑣2; 1. Укажите, какие из данных функций являются линейными? Определите скорость, при которой сопротивление будет наименьшим. 2. Изобразите схематически график линейной функции, заданной физической формулой Биология. Линейные зависимости величин в биологии Зависимость численности сине-зеленых водорослей от концентрации общего фосфора в воде выражается следующей формулой 𝑎 = 0,983𝑝 + 50,6 , где а – численность сине-зеленых водорослей, а p – концентрация общего фосфора Эту зависимость можно использовать для прогнозирования качества воды. Показателем качества воды служит количество сине-зеленых водорослей. Чем их больше, тем хуже качество воды. На численность сине-зеленых водорослей влияет концентрация фосфорного удобрения, стекающего в водоемы вместе с талой водой. Исходя из этой зависимости, можно дать рекомендации по внесению фосфорных удобрений для предотвращения ухудшения качества воды. Труд-девочки – тема «Пошив юбок». Изготовление чертежа выкройки. O m T Длина отрезка ОТ зависит от обхвата талии. Пусть m – длина отрезка ОТ n – обхват талии. Тогда зависимость m от n можно записать в виде формулы 𝑚 = 0,64𝑛 , где 0,64 – коэффициент для юбки. Построим схематически график данной функции. n 60 120 m 38,4 76,8 m, см 76,8 38,4 60 ≤ 𝑛 ≤ 120 n, см Учитель: Почему только первый квадрант? Какие значения может принимать n? почему? Что является графиком? Особенность расположения. (не начинается в начале координат) На осях n и m масштаб можно выбрать произвольно! Д/з Задача. Масса сосуда с жидкостью зависит от объема находящейся в ней жидкости. Обозначим через m0 – массу пустого сосуда 𝜌 - плотность жидкости 𝑉 - объем жидкости m – масса сосуда с жидкостью Зависимость m от V можно записать в виде формулы так 𝑚 = 𝑚0 + 𝜌𝑉 (Чтобы найти массу сосуда с жидкостью, надо к массе пустого сосуда прибавить массу жидкости 𝜌𝑉). 1. Является ли эта зависимость линейной функцией? 2.Построить график этой зависимости, если известно, что масса сосуда с 4л жидкости равна 8кг, а с 6л – 9кг. 3. По графику зависимости ответить на вопросы: а) какова масса пустого сосуда? б)какова масса сосуда с 2л жидкости? в)сколько литров жидкости в сосуде, если его масса 13 кг? г)какова масса 1л жидкости? Ответы: m, кг V, л 1.Масса пустого сосуда (V=0) равна 6 кг 2.Масса сосуда с 2л жидкости равна 7 кг 3.Если масса сосуда с жидкостью 13 кг, то в нем 14л жидкости 4.Масса 1л сосуда с жидкостью равна 6,5 кг Масса пустого сосуда равна 6 кг Значит масса 1л жидкости 6,5-6=0,5(кг)