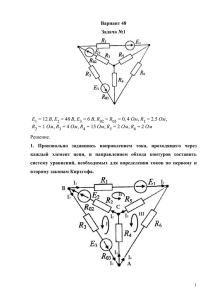
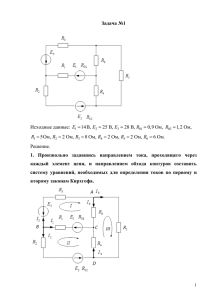
По исходным данным, необходимо:

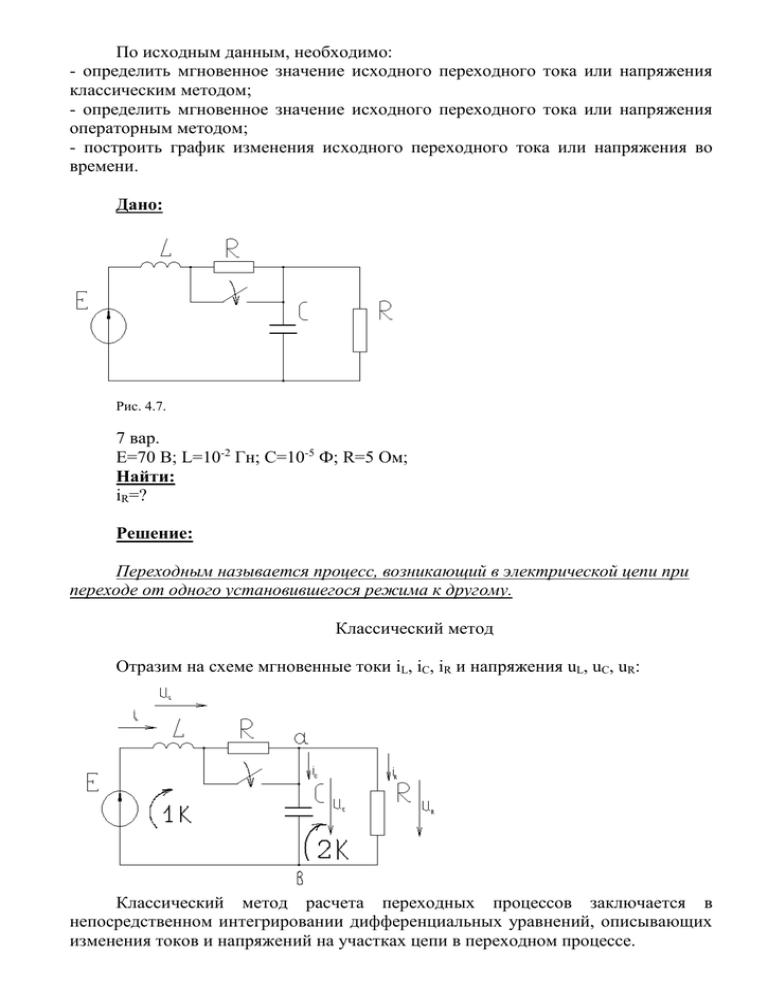
По исходным данным, необходимо:
- определить мгновенное значение исходного переходного тока или напряжения
классическим методом;
- определить мгновенное значение исходного переходного тока или напряжения
операторным методом;
- построить график изменения исходного переходного тока или напряжения во
времени.
Дано:
Рис. 4.7.
7 вар.
Е=70 В; L=10-2 Гн; C=10-5 Ф; R=5 Ом;
Найти:
iR=?
Решение:
Переходным называется процесс, возникающий в электрической цепи при
переходе от одного установившегося режима к другому.
Классический метод
Отразим на схеме мгновенные токи iL, iC, iR и напряжения uL, uC, uR:
Классический метод расчета переходных процессов заключается в
непосредственном интегрировании дифференциальных уравнений, описывающих
изменения токов и напряжений на участках цепи в переходном процессе.
В общем случае при использовании классического метода расчета
составляются уравнения электромагнитного состояния цепи по законам Ома и
Кирхгофа для мгновенных значений напряжений и токов.
Введем обозначения:
k – число узлов схемы
m – число ветвей, не содержащих источников тока
В рассматриваемом примере k = 2, m = 3.
Расчет и анализ сложной электрической цепи основан на уравнениях,
составляемых по 1 и 2 законам Кирхгофа, в количестве, достаточном для решения
системы. Все уравнения в системе должны быть независимыми.
Число независимых уравнений, составляемых по 1 закону Кирхгофа, на
единицу меньше числа узлов:
N óð ïî
N óð ïî
 k 1
1ç.
1ç.
 2 1  1
Число независимых уравнений, составляемых по второму закону Кирхгофа:
 m  N óð ïî
N óð ïî
2 ç.
N óð ïî
2 ç.
1ç.
 m  (k  1)
 3  (2  1)  2
Независимость уравнений по второму закону Кирхгофа будет обеспечена,
если контуры выбирать таким образом, чтобы каждый последующий контур
отличался от предыдущего хотя бы одной новой ветвью.
Для
контура, содержащего ветвь с источником тока, уравнение не
составляется.
Направление обхода – произвольное.
Уравнение по второму закону Кирхгофа для первого контура:
E=uL+uC; (1)
Уравнение по второму закону Кирхгофа для второго контура:
0=-uC+uR; (2)
Уравнение по первому закону Кирхгофа для узла «а»:
iL- iC- iR=0; (3)
Для R,L,C элементов схемы справедливы следующие соотношения,
связывающие мгновенные напряжения и токи:
diL (t )
dt
( 4)
1
iC (t )dt

C
(5)
uL  L
uC 
uR  iR (t )  R
(6)
Перепишем уравнения (1)-(3), используя соотношения (4)-(6):
diL (t ) 1

E

L
  iC (t )dt

dt
C

1

0    iC (t )dt  iR (t )  R
C

iL (t )  iC (t )  iR (t )  0


(7 )
(8)
(9)
Полученную систему решаем относительно искомой переменной iR(t).
Из (9) имеем:
diL (t ) diC (t ) diR (t )


0
dt
dt
dt
(10)
Из (7) имеем:
diL (t ) E 1
   iC (t )dt
dt
L C
(11)
Используя (8), выражение (11) перепишем:
diL (t ) E R
  iR (t )
dt
L L
(12)
Также из (8) после преобразований получаем:
diC (t )
d 2iR (t )
 CR
dt
dt 2
(13)
Далее, (12) и (13) подставляем в (10):
E R
d 2iR (t ) diR (t )
 iR (t )  CR

0
L L
dt 2
dt
d 2iR (t ) L diR (t )
E
LC



i
(
t
)

R
dt 2
R dt
R
(14)
Получили (14)-линейное неоднородное дифференциальное уравнение
второго порядка с постоянными коэффициентами. Решение будем искать как
сумму двух составляющих:
iR (t )  iR.ñâ(t )  iR.âûí (t )
Первая составляющая называется свободной или собственной и
определяется как общее решение соответствующего однородного уравнения,
которое получается из (14) заменой правой части нулю:
d 2iR.ñâ(t ) L diR.ñâ(t )
LC
 
 iR.ñâ(t )  0
2
dt
R
dt
Характеристическое уравнение:
(15)
LCp 2 
L
p 1  0
R
107  p 2  0,2 102  p  1  0
D  b  4ac  0,04  10 4  4  10 7  3,6 10 6
 b  D  0,2  10 2  1,8973  10 3
p1, 2 

2a
2 10 7
p1  513,17;
p2  19486,83;
Решение iR.св(t) будет в виде:
iR.ñâ (t )  A1  e p1t  A2  e p2t
iR.ñâ (t )  A1  e 513,17t  A2  e 19486,83t
Вторая составляющая iR.вын(t) называется вынужденной и представляет
собой частное решение неоднородного дифференциального уравнения (14) (с
ненулевой правой частью). Из математики известно, что вид частного решения
определяется видом правой части уравнения. В частности, если правая часть константа, то и частное решение ищется в виде константы.
Вынужденная составляющая называется установившейся и определяется при
t: iR.вын(t)=E/R;
Таким образом:
iR (t )  A1  e p1t  A2  e p2t 
E
R
Коэффициенты А1 и А2 найдем из начальных условий.
Согласно первому закону коммутации, ток в индуктивной катушке не может
изменяться скачкообразно:
iL (0 _)  iL (0  )  iL (0) 
E
2R
Но при t=0 iL(0)=iR(0), т.к. последовательное соединение L и R. Тогда:
E
E
 A1  e0  A2  e0 
2R
R
E
A1  A2  
(16)
2R
Из (8) имеем:
diR (t )
dt
iC (t )  CR( A1 p1  e p1t  A2 p2  e p2t )
iC (t )  CR
При t=0 постоянный ток через конденсатор не течет: iC(t)=0:
0  CR( A1 p1  e 0  A2 p2  e 0 )
A1 p1  A2 p2  0
(17)
E

 A1  A2  
2R


 A1 p1  A2 p2  0
Из (16) и (17) составляем систему и решаем ее относительно А1 и А2:
А2=0,1893
A1=-7,1893
Таким образом, получаем:
iR (t )  14  7,1893  e513,17t  0,1893  e19486,83t
( A)
Операторный метод
В основе операторного метода лежит преобразование Лапласа и
операционное исчисление, известные из курса высшей математики. Операторный
метод позволяет производить анализ переходных процессов при воздействии
сигналов любой формы и не требует определения постоянных интегрирования,
что существенно упрощает анализ электрических цепей, порядок которых выше
чем первый.
Решение задачи начинаем с изображения операторной цепи, которая
соответствует послекоммутационному состоянию цепи
Как известно, при ненулевых начальных условиях в соответствии со
свойствами преобразования Лапласа, имеем:
u L t   L
diL (t ) 
  U L  p   pLI L  p   LiL 0 
dt
u 0
U C  p   pCI C  p   C
p
Что и отражено на схеме.
Составляем систему уравнений по первому и второму законам Кирхгофа:
uC (0)
I C ( p)
E

i
(
0
)


pLI
(
p
)

(18)
L
p L
p
pC

I ( p)
 uC (0)
 C
 U R ( p)
(19)

p
pC

I L ( p)  I C ( p)  I R ( p)
(20)


Выразим IL(p) из (20) и подставим в (18), решим относительно IC(p):
CE  LpCiL (0)  CuC (0)  p 2 LCI R ( p)
I C ( p) 
1  p 2 LC
(21)
Решим (19) относительно IC(p):
I C ( p)  RpCI R ( p)  CuC (0)
(22)
Приравняв выражения (21) и (22), решим относительно IR(p):
p 2 LCuC (0)  pLiL (0)  E
I R ( p) 
(23)
p( RLCp 2  pL  R)
Подставляя исходные данные и начальные значения, имеем:
0,35 10 5 p 2  0,07 p  70
I R ( p) 
p(5 10 7 p 2  10 2 p  5)
(23)
Из курса высшей математики известно, что если изображение F(p) искомой
переменной определяется отношением двух полиномов
F ( p) 
F1 ( p) bm p m  bm1 p m1  ...  b1 p  b0

,
F2 ( p) a n p n  a n 1 p n 1  ...  a1 p  a0
ãäå m  n, òî
если один из корней уравнения F2(p)=0 (что мы имеем в нашем случае), т.е.
F2(p)=pF3(p), то оригинал ищем в виде:
f (t ) 
F1 (0) n F1 ( pk )

 e pk t ,
F3 (0) k 1 pk F3( pk )
F1 ( p)  0,35 105 p 2  0,07 p  70
F3 ( p )  5  10 7 p 2  10 2 p  5
F3 ( p)  0;
5 107 p 2  102 p  5  0
p1  513,167;
p2  19486,832
F3( p )  10 6 p  10 2
ãäå pk  k  é êîðåíü F3 ( p)
F1 (0)  70; F3 (0)  5;
F1 ( p1 )  F1 (513,17)  35; F3( p1 )  F3(513,17)  0,0094868;
F1 ( p2 )  F1 (19486,83)  35; F3( p2 )  F3(19486,83)  0,0094868;
iR (t ) 
70
35
35



5 (513,17)  0,0094868 (19486,832)  (0,0094868)
 14  7,1893  e 513,17t  0,1893  e 19486,83t ( À)
График зависимости iR(t) построен с использованием пакета MathCAD 2001 Pro: