Алгоритм МКТ

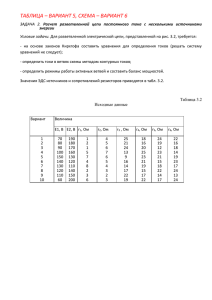
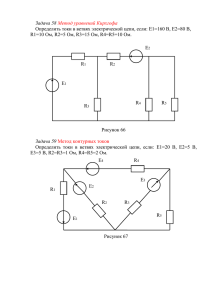
Лекция 3.
РАСЧЕТ СЛОЖНЫХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА.
Законы Кирхгофа.
1-й закон: Алгебраическая сумма токов ветвей, сходящихся
n – число элементов электрической цепи в составе
в узле равна нулю. Или: арифметическая сумма токов
рассматриваемого контура.
входящих в узел равна арифметической сумме токов
Или: алгебраическая сумма падений напряжений на
выходящих из узла.
приемниках энергии равна алгебраической сумме ЭДС в
n
составе контура
n
m
Ii  0 ,
i 1
Ui 
Ej ,
i 1
j 1
где
Ii – ток i-й ветви, подходящей к узлу,
n – число ветвей, сходящихся в узле.
где
Ui – падение напряжения на i-м приемнике
2-й закон: Алгебраическая сумма падений напряжений по
рассматриваемого контура (знак Ui определяется
любому замкнутому контуру электрической цепи равна
сопоставлением направления падения напряжения с
нулю.
направлением положительного направления обхода
n
контура),
Ui  0 ,
Ej – ЭДС j-го источника (знак Ei определяется
i 1
сопоставлением направления ЭДС с направлением
где
Ui – падение напряжения на i-м элементе
положительного направления обхода контура),
электрической цепи рассматриваемого контура (знак Ui
n – число элементов электрической цепи в составе
определяется сопоставлением направления падения
рассматриваемого контура.
напряжения с направлением положительного направления
обхода контура),




Метод уравнений Кирхгофа.
2. Для n – 1 узлов составляют уравнения на основании первого
з-на Кирхгофа; для одного из узлов такое уравнение не
составляют, поскольку оно является следствием уже
написанных уравнений.
Алгоритм метода уравнений Кирхгофа.
1.2. Правила Кирхгофа
Предположим, дана схема, содержащая m ветвей, n узлов,
ЭДС источников, их внутренние и внешние сопротивления.
Требуется определить токи в ветвях. Последовательность
расчета:
1. Для каждой ветви вводят обозначение протекающего
через нее тока I1, I2,…, Im и стрелками на схеме указывают
его условное положительное направление.
Рисунок 1
3. Берутся независимые контуры цепи (в каждом контуре
хотя бы в одной ветви ток не входит в другие контуры), в
которых выбираются условные положительные направления
обхода контура.
4. Для контуров составляют уравнения по второму правилу
Кирхгофа с учетом выбранного направления обхода. При
правильном выборе контуров их число должно быть m – n +
l. Общее число уравнений должно быть m (по числу
неизвестных).
5. Решается система m уравнений. Если рассчитанный ток в
ветви — положительный, то действительное направление
тока совпадает с выбранным и наоборот.
Пр и м ер (р ис. 1 ) . Схема содержит четыре узла и шесть
ветвей. Следовательно, полное число уравнений должно
равняться шести. Из них, на основании первого правила
Кирхгофа, составляем три уравнения. Остальные уравнения
получаем по второму правилу Кирхгофа.
Обозначим токи в ветвях и выберем направления токов.
Запишем уравнения на основании первого правила
Кирхгофа, например, для узлов a, b и e: I1+I2-I3 = 0; I3-I5-I6 =
0; I4-I1-I2 = 0.
В качестве независимых контуров для составления уравнений
по втором правилу Кирхгофа выбираем, например, контуры
aefa, abdea и bcdb. За положительное направление обхода
примем обход контуров по часовой стрелке. В результате
получим следующие уравнения:
E1  E2  I1  R1  I 2  R2 ;
E2  I 2  R2  I 3  R3  I 5  R5  I 4  R4 ;
E6   I5  R5  I 6  R6 .
Для шести неизвестных I1…. I6 получено шесть уравнений.
Решение системы рекомендуется начать с того, что из
первых трех уравнений можно выразить, например, токи I1,
I2, I3 через токи I4, I5, I6. После подстановки найденных
значений в последние три уравнения получим систему из
трех уравнений с тремя неизвестными. Остается решить
систему
Метод контурных токов.
2) реальные токи смежных ветвей определяются как
алгебраическая сумма смежных контурных токов;
знак контурного тока определяется сравнением его
направления с выбранным направлением реального
тока.
Знак полученного реального тока определяет правильность
выбора его направления.
Алгоритм МКТ
1. Выбираем
направления
контурных
токов,
совпадающих с направлениями обходов контуров.
Следует помнить: контуры выбираются,
не
содержащие идеальных источников тока!!!
2. Задаемся направлением токов в ветвях.
3. Составляем систему уравнений по МКТ
4. Определяем контурные токи
5. Вычисляем реальные токи в ветвях.
ПРИМЕР
J = 0,7 A E7 = 2 В
E1 = 4 В E2 = 1 В E6 = 5 В
R1 = 12 Ом R2 = 5 Ом
R4 = 4 Ом R5 = 4 Ом R3 = 2 Ом
R7 = 24 Ом R6 = 1 Ом
МКТ основан на идее определения не реальных токов, а так
называемых контурных токов. При этом предполагают, что
по каждому НЕЗАВИСЕМОМУ контуру течет свой
контурный ток, который течет только по элементам «своего»
контура и не разветвляется на узлах.
По МКТ значения контурных токов определяются из
системы уравнений, написанных по 2-му закону Кирхгофа.
Система уравнений по МКТ имеет следующий общий вид:
E1  R11 I1  R12 I 2 
 R1n I n 
E2  R21 I1  R22 I 2   R2 n I n 


En  Rn1 I1  Rn 2 I 2   Rnn I n 
где
Ei – контурная ЭДС в контуре i (i=1,2,…,n), т.е.
алгебраическая сумма ЭДС, действующих в данном контуре;
ЭДС, совпадающая по направлению с направлением
контурного тока, берутся со знаком +, и наоборот;
Rii – собственное сопротивление контура i;
Rik – общее сопротивление контуров i и k.
Реальные токи определяются по найденным контурным,
следуя следующему правилу:
1) реальные токи внешних ветвей контуров равны
контурным токам;
Решение:
1. Выбираем направления контурных токов, совпадающих с
направлениями обходов контуров.
Следует помнить: контуры выбираются, не содержащие
идеальных источников тока!!!
2. Задаемся направлением токов в ветвях.
3. Составляем систему уравнений по МКТ:
 R1  R2  R4  R3  I к  R3 I к  R4 I к  JR2  E2  E1
1
2
3

  R3 I к1   R3  R5  R6  I к 2  R5 I к 3  E6

 R4 I к1  R5 I к 2   R4  R5  R7  I к 3   E7
После подстановки численных значений система примет вид:
 23  I к  2  I к  4  I к  4  1  0,7  5
1
2
3

 2  I к1  7  I к 2  4  I к 3  5

 4  I к 1  4  I к 2  32  I к 3  2
При
направлении
СУ
необходимо
учитывать
взаимодействие контурного тока численно равного J - току
источника тока на смежных контурах с источником тока!!!
Определяем контурные токи:
Iх1 = 0,5А; Iх2 = 1А; Iх3 = –0,25А.
4. Вычисляем токи в ветвях:
I 1  I к1  0,5 A ; I 2  I к1  J  0,5  0,7 A  0, 2 A ;
I 3  I к2  I к1  1  0,5  0,5 A ; I 4  I к1  I к3  0, 25 A ;
I 5  I к3  I к2  0,75 A ; I 6  I к2  1 A ; I7   I к3  0, 25 A