Ragevine_RGZx

Федеральное государственное автономное
образовательное учреждение
высшего профессионального образования
«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
Институт Космических и Информационных Технологий
Системы автоматики, автоматизированного управления и проектирования
кафедра
РАСЧЕТНОЕ ЗАДАНИЕ
по дисциплине
Электротехника и электроника
Анализ резистивных цепей постоянного тока
тема
Преподаватель
___________ _______________
подпись, дата
Студент
инициалы, фамилия
__________ ______________ ___________ _______________
номер группы
номер зачетной книжки
Красноярск 2013
подпись, дата
инициалы, фамилия
Вариант 40
1. Записать уравнения по законам Кирхгофа. Решив полученную систему
уравнений, определить токи и напряжения ветвей.
2. Составить узловые уравнения цепи в матричной форме. Решив
составленные уравнения, рассчитать токи во всех ветвях исходной цепи.
3. Результаты расчетов свести в таблицу.
4. Рассчитать ток в ветви с резистором Rk методом эквивалентного
генератора.
5. Определить, при каком сопротивлении резистора Rk опт в нем выделяется
максимальная мощность.
6. Построить графики зависимостей тока, напряжения и мощности,
выделяемой в резисторе Rk при изменении сопротивления от 0.1 Rk опт до
10 Rk опт .
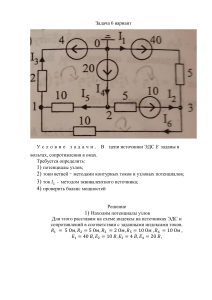
Схема (Рис. 1.4) :
Дано:
R1 = 6 Ом
R2 = 17,5 Ом
R3 = 2 Ом
R4 = 3 Ом
R5 = 5 Ом
R6 = 7,5 Ом
Rk = 6 Ом
E2 = 6,5 В
J2 = 0,2 A
J3 = 0,4 A
K=4
S = 0,4
(Последний номер
зачетной книжки - 4)
Задание 1
Произвольно выбираем направления токов, а также контуры и направления обхода
для составления уравнений по законам Кирхгофа. Обозначим это на схеме:
Запишем уравнения по первому закону Кирхгофа для узлов a, b, d. Токи,
направленные от узла, записываем со знаком «+». Токи, направленные к узлу, записываем
со знаком «−».
Для узла a:
Для узла b:
Для узла с:
−𝐼1 + 𝐼2 + 𝐼6 + 𝐽2 = 0
𝐼3 + 𝐼4 − 𝐼6 − 𝐽3 = 0
−𝐼2 − 𝐼4 + 𝐼5 − 𝐽2 = 0.
Запишем уравнения по второму закону Кирхгофа для контуров I, II, III.
Для контура I:
−𝑅2 𝐼2 + 𝑅4 𝐼4 + 𝑅6 𝐼6 = −𝐸2
Для контура II:
𝑅1 𝐼1 + 𝑅2 𝐼2 + 𝑅5 𝐼5 = 𝐸2
Для контура III:
𝑅3 𝐼3 − 𝑅4 𝐼4 − 𝑅5 𝐼5 = −𝐾𝑈𝑐𝑑
Где 𝐾𝑈𝑐𝑑 = 𝐾𝑅5 𝐼5
Таким образом, получаем следующую систему уравнений:
−𝐼1 + 𝐼2 + 𝐼6 = −𝐽2
𝐼3 + 𝐼4 − 𝐼6 = 𝐽3
−𝐼2 − 𝐼4 + 𝐼5 = 𝐽2
−𝑅2 𝐼2 + 𝑅4 𝐼4 + 𝑅6 𝐼6 = −𝐸2
𝑅1 𝐼1 + 𝑅2 𝐼2 + 𝑅5 𝐼5 = 𝐸2
{𝑅3 𝐼3 − 𝑅4 𝐼4 + (𝐾 − 1)𝑅5 𝐼5 = 0
В матричной форме:
−1
1
0
0
0
−1
0 −𝑅2
𝑅1
𝑅2
0
[0
0
1
0
0
0
𝑅3
0
1
−1
𝑅4
0
−𝑅4
0
0
1
0
𝑅5
(𝐾 − 1)𝑅5
1
𝐼1
−𝐽2
−1
𝐼2
𝐽3
0
𝐼3
𝐽2
𝑅6 ∗ 𝐼4 = −𝐸2
0
𝐼5
𝐸2
0 ] [𝐼6 ] [ 0 ]
Полученная матрица в числовой форме:
−1
1
0 0
0
0
1 1
0
−1
0 −1
0 −17,5 0 3
6
17,5 0 0
[0
0
2 −3
𝐼1
0
1
−0,2
𝐼2
0
−1
0,4
𝐼
1
0
0,2
∗ 3 =
𝐼
0
7,5
−6,5
4
𝐼
5
0
6,5
5
]
[
[𝐼6 ]
−15 0
0 ]
Решив систему линейных уравнений, получили следующие результаты:
𝐼1 = 0,265 А
𝐼2 = 0,242 А
𝐼3 = 0,532 А
𝐼4 = −0,31 А
𝐼5 = 0,133 А
𝐼6 = −0,177 А
𝑈1 = 𝑅1 𝐼1 = 1,59 𝐵
𝑈2 = 𝐸2 − 𝑅2 𝐼2 = 2,265 𝐵
𝑈3 = 𝑅3 𝐼3 − 𝐾𝑈𝑐𝑑 = 0,399 𝐵
𝑈4 = 𝑅4 𝐼4 = −0,93 𝐵
𝑈5 = 𝑅5 𝐼5 = 0,665 𝐵
𝑈6 = −𝑅6 𝐼6 = 1,328 𝐵
Задание 2
Составить узловые уравнения цепи в матричной форме. Решив составленные
уравнения, рассчитать токи во всех ветвях исходной цепи.
Преобразуем цепь на рис. 1 к виду, удобному для анализа методом узловых
напряжений. Последовательные ветви источник напряжения - резистор преобразуем в
параллельную ветвь с источником тока.
Выберем узел b в качестве базисного. Остальные узлы обозначим c – 1, a – 2, d – 3.
Относительно базисного узла определяем направление узловых
напряженийV1 , V2 , V3 .Обозначим это на схеме:
Последовательно просматриваем ветви схемы. Если k-я ветвь включена между
узлами i и j, то проводимость этой ветви войдёт в элементы матрицы узловых
проводимостей, которые находятся на пересечении строк и столбцов с номерами i и j. На
главной диагонали все проводимости записываем со знаком «+», вне главной диагонали
со знаком «−». Процедура составления уравнений заканчивается, когда рассмотрены все
ветви.
Матрица узловых проводимостей цепи:
𝐺2 + 𝐺4 + 𝐺5
−𝐺2
[𝐺] = [
−𝐺5 − 𝐾𝐺3
−𝐺2
𝐺1 + 𝐺2 + 𝐺6
−𝐺1
−𝐺5
−𝐺1
]
𝐺1 + 𝐺3 − 𝐾𝐺3 + 𝐺5
Система уравнений по методу узловых напряжений:
𝐺2 + 𝐺4 + 𝐺5
−𝐺2
[
−𝐺5 − 𝐾𝐺3
−𝐺2
𝐺1 + 𝐺2 + 𝐺6
−𝐺1
Решив её, получили:
𝑉1 = 0.605 В
𝑉2 = –1.765 В
𝑉3 = –0.564 В
Найдём токи в ветвях:
I1 = (V3 – V2)G1 = 0,2
I2 = (V2 –V1 + E2)G2 = 0,236
I3 = (–V2–KUcd)G3 = 0,448
I4 = V1G4 = –0,202
I5 = (V1 – V3)G5 = 0,234
I6 = V2 G6 = -0,235
−𝐺5
𝐽2 + 𝐸2 /𝑅2
V1
−𝐺1
] ∗ [V2 ] = [−𝐽2 − 𝐸2 /𝑅2 ]
V3
𝐺1 + 𝐺3 − 𝐾𝐺3 + 𝐺5
−𝐽3
Задание 3
i
1
2
3
4
5
6
Величины, найденные по
законам Кирхгофа
Ii , A
Vi , В
0,265
1,59
0,242
2,265
0,532
0,399
−0,31
−0,93
0,133
0,665
−0,177
1,328
Величины, найденные по
методу узловых напряжений
Ii , A
Vi , В
0,2
0.605
–1.765
0,236
–0.564
0,448
–0,202
0,234
–0,235
Задание 4
По условию, k = 1. Поэтому выделяем 1-ю ветвь, остальную часть цепи заменяем
эквивалентным двухполюсником:
В этой схеме Ег = 𝑈хх , где 𝑈хх - напряжение холостого хода
R г = R вх , где R вх – входное сопротивление цепи
Ток на 6-ом резисторе можно найти по формуле:
𝐼1 =
Eг
R г + R1
Определим параметры генератора. Сначала найдём 𝑈хх :
Для этого можно воспользоваться уравнениями по законам Кирхгофа,
составленным в 1-м пункте, учитывая, что 𝑅1 𝐼1 = 𝑈хх , 𝐼1 = 0 (цепь на участке b – d
разомкнута). Сразу запишем систему уравнений:
𝐼2 + 𝐼6 = −𝐽2
𝐼3 + 𝐼4 − 𝐼6 = 𝐽3
−𝐼2 − 𝐼4 + 𝐼5 = 𝐽2
−𝑅2 𝐼2 + 𝑅4 𝐼4 + 𝑅6 𝐼6 = −𝐸2
𝑈𝑥𝑥 + 𝑅2 𝐼2 + 𝑅5 𝐼5 = 𝐸2
{𝑅3 𝐼3 − 𝑅4 𝐼4 + (𝐾 − 1)𝑅5 𝐼5 = 0
Решив её, получили
𝑈хх = 3.096 В
Теперь найдём R вх . В цепи с управляемыми источниками входное сопротивление
можно найти только как отношение напряжения холостого хода к току короткого
замыкания:
R вх =
𝑈хх
𝐼кз
Снова можно воспользоваться уравнениями по законам Кирхгофа, составленным в
1-м пункте, учитывая, что 𝐼1 = 𝐼кз , 𝑅1 = 0 (цепь на участке b – d закорочена). Сразу
запишем систему уравнений:
𝐼кз + 𝐼2 + 𝐼6 = −𝐽2
𝐼3 + 𝐼4 − 𝐼6 = 𝐽3
−𝐼2 − 𝐼4 + 𝐼5 = 𝐽2
−𝑅2 𝐼2 + 𝑅4 𝐼4 + 𝑅6 𝐼6 = −𝐸2
𝑅2 𝐼2 + 𝑅5 𝐼5 = 𝐸2
{𝑅3 𝐼3 − 𝑅4 𝐼4 + (𝐾 − 1)𝑅5 𝐼5 = 0
Решив её, получили
𝐼кз = −0.546 А.
Находим
R вх =
𝑈хх
= 5.67 Ом.
𝐼кз
Определив параметры генератора, можем посчитать ток на 1-м резисторе:
𝐼1 =
Eг
= 0,265 А
R г + R1
5. Определить, при каком сопротивлении резистора 𝐑 к в нем выделяется
максимальная мощность.
Известно, что мощность, выделяющуюся на резисторе, можно найти по формуле
𝑃 = 𝑅𝐼 2 . А силу тока на 6-м резисторе мы находили по формуле 𝐼1 =
это выражение в формулу нахождения мощности, получим:
𝑃 = 𝑅1 𝐼12 = Eг2
Eг
Rг + R1
. Подставив
R1
.
(R г + R1 )2
Предположим, что R1 = R 𝑥 - неизвестная величина. Тогда мы получим функцию
мощности 𝑃(R 𝑥 ), зависящую от сопротивления R 𝑥 . Исследуя эту функцию с помощью
производной, мы находим значение, при котором 𝑃(R 𝑥 ) принимает максимальное
значение (оптимальное сопротивление резистора R1 , при котором в нём выделяется
максимальная мощность). Это значение
R x =R опт = R г = 3,5468 Ом.
6. Построить графики зависимостей тока, напряжения и мощности, выделяемой в
резисторе 𝐑 к при изменении сопротивления от 𝟎, 𝟏𝐑 опт до 𝟏𝟎𝐑 опт .
Рис. 7. График зависимости I1(Rг)
Рис. 8. График зависимости U1(Rг)
Рис. 9. График зависимости P1(Rг)