Контрольная работа

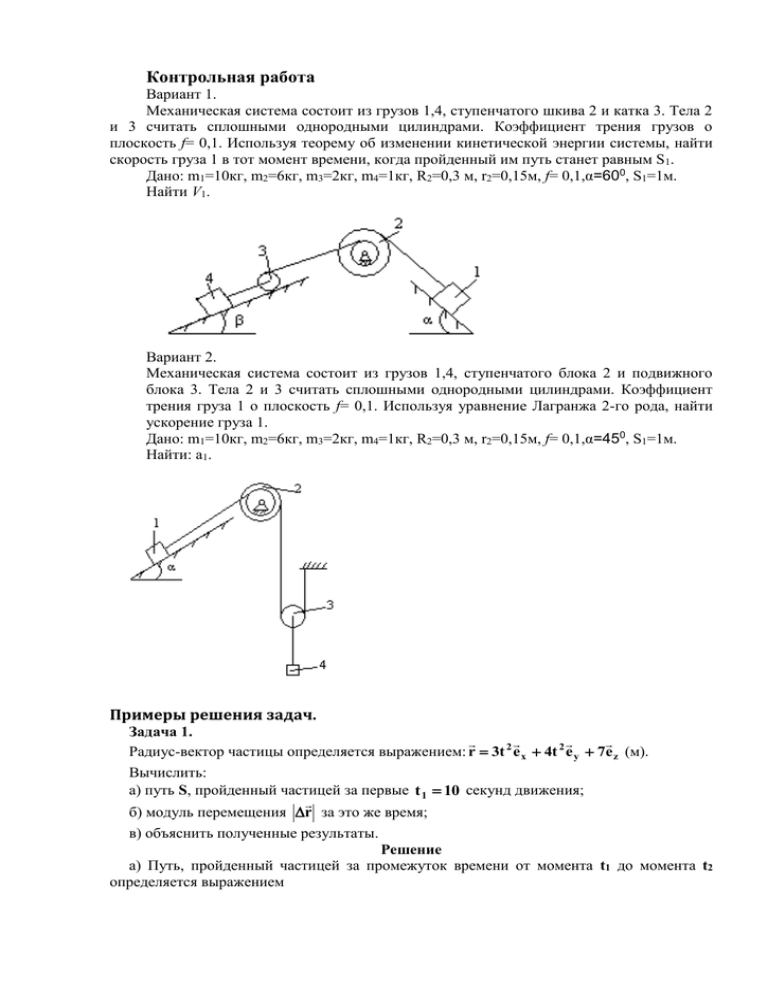
Контрольная работа
Вариант 1.
Механическая система состоит из грузов 1,4, ступенчатого шкива 2 и катка 3. Тела 2
и 3 считать сплошными однородными цилиндрами. Коэффициент трения грузов о
плоскость f= 0,1. Используя теорему об изменении кинетической энергии системы, найти
скорость груза 1 в тот момент времени, когда пройденный им путь станет равным S1.
Дано: m1=10кг, m2=6кг, m3=2кг, m4=1кг, R2=0,3 м, r2=0,15м, f= 0,1,α=600, S1=1м.
Найти V1.
Вариант 2.
Механическая система состоит из грузов 1,4, ступенчатого блока 2 и подвижного
блока 3. Тела 2 и 3 считать сплошными однородными цилиндрами. Коэффициент
трения груза 1 о плоскость f= 0,1. Используя уравнение Лагранжа 2-го рода, найти
ускорение груза 1.
Дано: m1=10кг, m2=6кг, m3=2кг, m4=1кг, R2=0,3 м, r2=0,15м, f= 0,1,α=450, S1=1м.
Найти: а1.
Примеры решения задач.
Задача 1.




Радиус-вектор частицы определяется выражением: r  3t 2 e x  4t 2 e y  7e z (м).
Вычислить:
а) путь S, пройденный частицей за первые t 1  10 секунд движения;

б) модуль перемещения r за это же время;
в) объяснить полученные результаты.
Решение
а) Путь, пройденный частицей за промежуток времени от момента t1 до момента t2
определяется выражением
t2
S   V t dt ,
t1
V t   Vx2  Vy2  Vz2
где
-
модуль
скорости
частицы,
а
ее
проекции
dy
dx
dv
. В нашем случае xt   3t 2 , y t   4t 2 , z t   7 , поэтому
, vy 
, vz 
dt
dt
dz
v x  6t , v y  8t , v z  0 , а модуль скорости v = 10t. Проводя интегрирование, получим:
vx 




S  5 t 22  t 12 или S  5 10 2  0  500 м
б) Модуль перемещения определяется выражением:

r 
t2

 vt dt 
t2
t1
t1
 dx 
dy 
dz  
  dt e x  dt e y  dt e z dt




 x 2  x 1 e x  y 2  y 1 e y  z 2  z 1 e z
или

r 

x 2  x1 2  y 2  y 1 2  z 2  z 1 2
3t
2
2
  4t  4t   7  7
 5t  t   S (см. п.а))
2
 3t 12
2
2
Fn
Fтр
R 0

2
2
2 2
1
2


2
1
в) Так как для любого промежутка

времени получено равенство S  r ,
это означает, что частица движется по
прямолинейной траектории, не изменяя
направления движения.
mg sin 
Задача 2.
Пусть однородный цилиндр радиуса
h
R и массы m скатывается без
mg cos
vo

скольжения с наклонной плоскости
mg
(рис. 4.14). Угол наклона плоскости

равен , а высота h (h >> R). Начальная
скорость цилиндра равна нулю.
Рис. 4.14
Требуется найти скорость центра
инерции и угловую скорость вращения
цилиндра в момент выхода цилиндра на горизонтальный участок. Дадим два варианта
решения.


1-й способ решения. Цилиндр будет двигаться под действием трех сил, силы P  mg ,


силы трения Fтр и силы нормального давления Fn . Ускорение цилиндра в направлении
нормали к плоскости равно нулю. Следовательно, сила нормального давления равна по

модулю нормальной составляющей силы P , имеющей величину mg cos  .
Трение между цилиндром и плоскостью возникает в точках их соприкосновения. При
отсутствии скольжения эти точки цилиндра неподвижны (они образуют мгновенную ось
вращения), следовательно, сила трения, о которой идет речь, является силой трения покоя.
Известно, что сила трения покоя может иметь величину в пределах от нуля до
максимального значения F0, которое определяется произведением коэффициента трения
на силу нормального давления, прижимающую друг к другу соприкасающиеся тела (
F0  kmg cos  ). В рассматриваемом случае сила трения принимает такое значение, чтобы
отсутствовало скольжение. Скольжение при качении цилиндра по плоскости будет
отсутствовать при условии, что линейная скорость точек соприкосновения будет равна
нулю, что в свою очередь выполняется, если скорость центра инерций vc равна каждый
момент времени угловой скорости вращения цилиндра , умноженной на радиус
цилиндра R:
(4.82)
v c  R .
Соответственно ускорение центра инерции ас будет равно угловому ускорению 
умноженному на R:
(4.83)
a c  R .
Если необходимая для выполнения условий (4.82) и (4.83) сила трения не превышает
максимального значения F0, цилиндр будет скатываться без скольжения. В противном
случае скатывание без скольжения невозможно.
Уравнение (4.51) в данном случае имеет вид:


 
ma c  mg  Fтр  Fn .
Спроектировав его на направление движения, получим
ma c  mg sin   Fтр .
(4.84)


Для однородного цилиндра, вращающегося вокруг оси симметрии, L  I . Поэтому
уравнение его вращательного движения можно писать в виде
(4.85)
I   M z ,
где z —ось цилиндра (см. (4.60)). В уравнении (4.85), написанном относительно оси
цилиндра, отличным от нуля будет только момент силы трения. Остальные силы, в том
числе и результирующая сил инерции, имеют направления, проходящие через ось
цилиндра, вследствие чего их моменты относительно этой оси равны нулю. Таким
образом, уравнение (4.85) запишется следующим образом:
I  RFтр
(4.86)
mR 2
.
2
В уравнениях (4.84) и (4.86) содержатся три неизвестные величины, FТР, c и .
Последние две величины связаны условием (4.83), вытекающим из отсутствия
скольжения. Решив совместно уравнения (4.83), (4.84) и (4.86), найдем (с учетом того, что
mR 2
I
) значения искомых величин:
2
1
Fтр  mg sin  ,
(4.87)
3
2
a c  g sin  ,
(4.88)
3
2 g 
    sin  .
(4.89)
3R
Теперь, когда мы знаем величину силы трения покоя, необходимую для скатывания
цилиндра без скольжения, можно найти условие, при котором такое скатывание
возможно. Для скатывания без скольжения сила (4.87) не должна превышать
максимального значения силы трения покоя F0, равного kmg cos  :
1
mg sin   kmg cos  .
3
Отсюда
tg  3k .
Следовательно, еcли тангенс угла наклона плоскости превышает утроенное значение
коэффициента трения покоя между цилиндром и плоскостью, скатывание не может
Здесь I — момент инерции цилиндра относительно его оси, равный
происходить без скольжения.
Из постоянства ас (см. (4.88)) следует, что центр инерции цилиндра движется
h
равноускоренно. За время скатывания tск цилиндр проходит путь
. При
sin 
at 2
равноускоренном движении путь, ускорение и время связаны соотношением s 
.
2
Подставив значение s, получим, что
h
1
2
 a c  t cк
.
sin  2
откуда с учетом значения (4.88) для ас приходим к формуле:
1
3h
.
t ск 
sin  g
Это время, как и ас, не зависит от массы и радиуса цилиндра; оно определяется только
углом наклона плоскости  и разностью уровней ее краев h.
Скорость центра инерции при выходе цилиндра на горизонтальный участок будет
равна
4
v c  a c t ск 
gh ,
3
а угловая скорость цилиндра
1 4
  t ск 
gh .
R 3
Отметим, что сила трения покоя работы над цилиндром не совершает, так как точки
цилиндра, к которым приложена эта сила, каждый момент времени- неподвижны.
При решении задачи о скатывании цилиндра с наклонной плоскости трением качения
мы пренебрегали.
2-й способ решения. Поскольку сила трения работы не совершает (трением качения
пренебрегаем), полная энергия цилиндра остается постоянной. В начальный момент
кинетическая анергия равна нулю, потенциальная энергия равна mgh. В конце скатывания
потенциальная энергия становится равной нулю, зато появляется кинетическая энергия,
равная
mv c2 I c  2
T

.
2
2
Так как скольжение отсутствует, VС и  связаны соотношением vс = R. Подставив в
vc
mR 2
выражение для кинетической энергии  
и Ic 
, получим:
2
R
mv c2 mv c2 3
T

 mv c2 .
2
4
4
Полная энергия в начале и в конце скатывания должна быть одинакова:
3
mv c2  mgh ,
4
откуда
4
vc 
gh ,
3
а угловая скорость
vc 1 4

gh .
R R 3
Обратите внимание, насколько второй способ решения проще первого.

Примеры задач для самостоятельного решения
Задача 1.




v 1  1e x  3e y  5e z (м/c),
Начальное
значение
скорости
равно
конечное





v 2  2e x  4e y  6e z (м/с). Найти: а) приращение скорости v , б) модуль приращения


скорости v , в) приращение модуля скорости  v .
Задача 2.
Потенциальная энергия частицы в некотором силовом поле определяется выражением
U=1,00x+2,00y2+3,00z3 (U в Дж, координаты в м). Найти работу А, совершаемую над
частицей силами при переходе из точки с координатами (1,00; 1,00; 1,00) в точку с
координатами (2,00; 2,00; 2,00).
Задача 3.
Четыре одинаковых шара массы m = 0,300 кг каждый объединены попарно с помощью
невесомых стержней длины  = 1,000м в две гантели.
Размеры шаров много меньше, чем  ; поэтому можно

считать материальными точками. Гантели движутся
поступательно навстречу друг другу с одинаковой
m
m
скоростью v = 1,000 м/с (рис 4.15). Считая удар шаров
v
v
мгновенным и абсолютно упругим,
v
v
а)
охарактеризовать
движение
гантелей
после m
m
столкновения,

б) найти угловую скорость  вращения гантелей,
в) определить время , в течении которого происходит
это вращение,
г) охарактеризовать движение гантелей по истечении
Рис. 4.15
времени .
Задача 4.
Найти отношение моментов инерции:
а) пирамиды (с квадратным основанием) и конуса одинаковой высоты, плотности и массы,
б) куба и шара одинаковой плотности и массы (у куба, как у шара, момент инерции
относительно любой проходящей через центр оси одинаков).
Имеются в виду оси, проходящие через вершину и центр основания в случае а) и
проходящие через центр в случае б).
Задача 5.
На столе стоит цилиндрический сосуд высоты H, наполненный доверху водой.
Пренебрегая вязкостью воды, определить высоту h, на которой нужно сделать в сосуде
небольшое отверстие, чтобы вытекающая из него струя попадала на стол на наибольшем
удалении от сосуда.