моделирование контактного взаимодействия

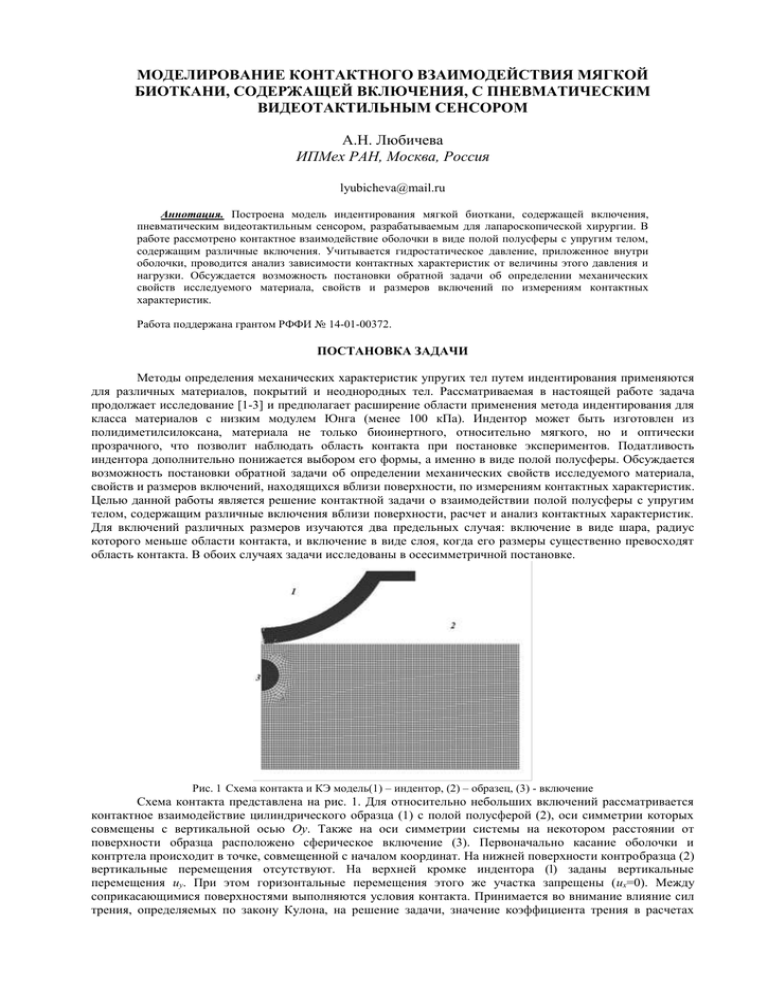
МОДЕЛИРОВАНИЕ КОНТАКТНОГО ВЗАИМОДЕЙСТВИЯ МЯГКОЙ
БИОТКАНИ, СОДЕРЖАЩЕЙ ВКЛЮЧЕНИЯ, С ПНЕВМАТИЧЕСКИМ
ВИДЕОТАКТИЛЬНЫМ СЕНСОРОМ
А.Н. Любичева
ИПМех РАН, Москва, Россия
[email protected]
Аннотация. Построена модель индентирования мягкой биоткани, содержащей включения,
пневматическим видеотактильным сенсором, разрабатываемым для лапароскопической хирургии. В
работе рассмотрено контактное взаимодействие оболочки в виде полой полусферы с упругим телом,
содержащим различные включения. Учитывается гидростатическое давление, приложенное внутри
оболочки, проводится анализ зависимости контактных характеристик от величины этого давления и
нагрузки. Обсуждается возможность постановки обратной задачи об определении механических
свойств исследуемого материала, свойств и размеров включений по измерениям контактных
характеристик.
Работа поддержана грантом РФФИ № 14-01-00372.
ПОСТАНОВКА ЗАДАЧИ
Методы определения механических характеристик упругих тел путем индентирования применяются
для различных материалов, покрытий и неоднородных тел. Рассматриваемая в настоящей работе задача
продолжает исследование [1-3] и предполагает расширение области применения метода индентирования для
класса материалов с низким модулем Юнга (менее 100 кПа). Индентор может быть изготовлен из
полидиметилсилоксана, материала не только биоинертного, относительно мягкого, но и оптически
прозрачного, что позволит наблюдать область контакта при постановке экспериментов. Податливость
индентора дополнительно понижается выбором его формы, а именно в виде полой полусферы. Обсуждается
возможность постановки обратной задачи об определении механических свойств исследуемого материала,
свойств и размеров включений, находящихся вблизи поверхности, по измерениям контактных характеристик.
Целью данной работы является решение контактной задачи о взаимодействии полой полусферы с упругим
телом, содержащим различные включения вблизи поверхности, расчет и анализ контактных характеристик.
Для включений различных размеров изучаются два предельных случая: включение в виде шара, радиус
которого меньше области контакта, и включение в виде слоя, когда его размеры существенно превосходят
область контакта. В обоих случаях задачи исследованы в осесимметричной постановке.
Рис. 1 Схема контакта и КЭ модель(1) – индентор, (2) – образец, (3) - включение
Схема контакта представлена на рис. 1. Для относительно небольших включений рассматривается
контактное взаимодействие цилиндрического образца (1) с полой полусферой (2), оси симметрии которых
совмещены с вертикальной осью Oy. Также на оси симметрии системы на некотором расстоянии от
поверхности образца расположено сферическое включение (3). Первоначально касание оболочки и
контртела происходит в точке, совмещенной с началом координат. На нижней поверхности контробразца (2)
вертикальные перемещения отсутствуют. На верхней кромке индентора (l) заданы вертикальные
перемещения uy. При этом горизонтальные перемещения этого же участка запрещены (ux=0). Между
соприкасающимися поверхностями выполняются условия контакта. Принимается во внимание влияние сил
трения, определяемых по закону Кулона, на решение задачи, значение коэффициента трения в расчетах
варьируется. Замыкают систему условия равновесия. Необходимо отметить, что задачи рассматриваются в
предположении о несжимаемом поведении исследуемых материалов. Модуль упругости материала
оболочки E1 = 2300 кПа (здесь и в дальнейшем индексом 1 будем отмечать характеристики индентора, а
индексом 2 – материала, контактирующего с ним). Коэффициент Пуассона составляет 1 = 0,4
В случае, когда включение существенно превышает область контакта однородного тела и оболочки,
предлагается модель в виде двухслойного упругого тела, нижний слой которого является более твердым, чем
верхний. Толщина верхнего слоя, соответствующая глубине локализации крупного включения, в расчетах
варьируется от одной десятой величины области контакта до удвоенного ее размера. Граничные условия
аналогичны условиям задачи о шаровом включении.
В постановках задач предусматривается возможность управления податливостью оболочки с
помощью гидростатического давления, приложенного к ее внутренней поверхности.
Задачи решаются в рамках теории упругости для несжимаемого тела с привлечением метода
конечных элементов. В расчетах используются несколько значений размеров включения (его радиуса в
первом случае и толщины слоя во втором), варьируется глубина локализации и отношение упругих свойств
окружающего материала и включения.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
В результате расчетов построены зависимости размера области контакта, контактного давления от
взаимного сближения индентора и образца для нескольких величин размераа включения, глубины его
расположения, соотношений модулей упругости включения и окружающего материала, а также для
различного гидростатического давления внутри оболочки. Анализ полученных результатов показал, что при
наличии более твердой неоднородности, радиус которой меньше области контакта, значение максимального
давления существенно увеличивается. При этом значительного изменения размеров области контакта, а
также взаимного сближения индентора и исследуемого образца не происходит. Представлен анализ
зависимости контактных характеристик от гидростатического давления внутри оболочки. Определен
диапазон варьируемых величин, в котором чувствительность метода позволяет сделать заключение о наличии
включения.
Рис. 2 Распределение контактных давлений при давлении внутри оболочки 15 кПа (кривые 1,2) и 6 кПа (кривые 3,4), для
значений осадки индентора: 1,7мм (кривые 2, 4), 0,25(кривая 1), 0,15 (кривая 3).
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований
(РФФИ 14-01-00372 А).
Литература
1.
2.
3.
И.Г. Горячева, Ю.Г. Мартыненко, Су Фон-Чин, М.Ю. Рязанцева, Ф.К. Антонов, //Российский журнал биомеханики. —
2013, 17, № 1, 8—21
Yeh, C.-H., Su, F.-C., Goryacheva, I., Martynenko, Y., Dosaev, M.Z., Ju, M.-S., // Sensors and Actuators A:
Physical 2014, 212, 42-51
Dosaev, M., Goryacheva, I., Su, F.C., Yeh, C.H., Ju, M.S., Gubenko, M., Lyubicheva, A., Morozov, A., Selyutskiy,
Y.//In: Flores, P., Viadero, F. (Eds.), New Trends in Mechanism and Machine Science. Springer International
Publishing, 2015, pp. 623-631