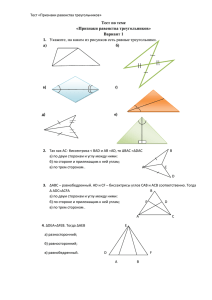
Тема урока: Решение задач на применение признаков

Выполнила учитель
Второй квалификационной категории
Самигуллина Ирина Анатольевна
Слайд №1
Тема урока: Решение
задач на применение признаков
равенства треугольников.
Слайд №2
Цели урока:
 Обучающая:, закрепить навыки использования признаков при решении
задач. Систематизировать, расширить и углубить знания учащихся о
треугольнике, закрепить навыки и умения при решении задач,
используя определения и теоремы по данной теме.
 Развивающая: развивать математическую речь учащихся, их память,
внимание,
наблюдательность,
умение
сравнивать,
обобщать,
обоснованно делать выводы, развивать умение преодолевать трудности
при решении задач, а также познавательный интерес учащихся.
Воспитательная: воспитание навыков контроля и самоконтроля, воспитание
правильной самооценки, аккуратности, внимательности, положительное
отношение к обучению, честности.
Слайд №3
Ход урока
1. Организационный момент
2. Опрос
3.Объяснение нового материала
4.Закрепление
5. Домашнее задание
Слайд №4
Если вы хотите научиться плавать, то смело входите в воду,
а если хотите научиться решать задачи, то решайте их.
(Д.Пойа)
1. Два ученика готовят на доске доказательство теоремы (II и III признак.)
Сформулируйте первый признак равенства треугольников.
Сформулируйте второй признак равенства треугольников.
Сформулируйте третий признак равенства треугольников.
Сколько равных пар сторон надо найти, доказываю равенство двух
треугольников?
А) по первому признаку
Б) по второму признаку
В) по третьему признаку
2.
3.
4.
5.
Слайд №5
Решение задач
Треугольники изображённые на рисунке.
А) равны по 2 сторонам и углы между ними;
Б) равны по стороне и 2 прилежащим к ней углам;
В) равны АО 3 сторонам;
Г) не равны
Слайд №6
Докажите равенство треугольников ABC и AMK
Слайд №7
№3
В равнобедренном
треугольнике ABC точка D середина основания AC. На лучах AB и
CB вне треугольника ABC отмечены точки M и N соответственно
так, что BM = BN.
Слайд №8
Проверка решения задачи
Доказать: треугольник BDM = треугольнику BDN
Доказательство:
1) треугольник ABC –равнобедренный, D – середина AC
следственно BD – медиана и биссектриса треугольника ABC
следственно <ABD = <CBD.
2) <NBA = <CBM (вертик)
<NBD = <NBA + < ABD
<MBD= <MBC + <CBD
Так как < ABD = <CBD
<MBC = <NBA то <NBD = <MBD
Треугольник NBD = треугольнику MBD по двум сторонам и углу
между ними так как NB = MB, BD – общая, < NBD = <MBD.
Ч.Т.Д.
Слайд №9
Рассмотрим чертёж. Заполните пропуски в таблице таким образом,
чтобы получить объяснение равенства приведённых в таблице пар
треугольников (образец заполнения показан на слайде)
Равные
треугольники
∆ AOB = ∆ COD
Соответственно
равные стороны
Соответственно
равные углы
Признак
равенства
AO = OC
BO = OD
<DOM = < COM
По двум
сторонам и углу
между ними
Слайд №10
Равные
треугольники
Соответственно
равные углы
Признак
равенства
По двум
сторонам и
углу между
ними
По двум
сторонам и
углу между
ними
∆ AOB = ∆ COD
AO = OC
BO = OD
<AOB = < COD
(Вертикальные)
1.
∆ DOM = ∆ COM
AO = OC
BO = OD
<DOM = < COM
2.
∆ COM = ∆ ANO
AO=OC
<OAM = < MCO
<AON = < COMвертикальные
3.
∆ ABC = ∆ ADC
AC-общая
<DCA = < CAB
<CAD = < BCA
4.
∆ AOD = ∆ BOC
AO=OC
DO=OC, AD=BC
-
По трём
сторонам
5.
∆ ADC = ∆ BDC
AB=DC
DA=DC, AC-общая
-
По трём
сторонам
По стороне
и двум
прилежащим
углам
По стороне
и двум
прилежащим
углам
После заполнения таблицы проверка записи в тетради, ребята
самостоятельно себя оценивают (критерий оценивания «5»- 5 заданий, «4» 4 - задания, «3» - задания меньше трех заданий оценка 2).
Задание: ( один из номеров домашнего задания, зачитывается в конце урока)
Прослушать рассказ ученика седьмого класс. Определить ошибки и написать
свой рассказ на данную тему.(зачитывается 2 раза )
Рассказ семиклассника на тему «Что такое треугольник»
«Треугольник-это такая фигура, где всего по трое: три стороны; вершин,
углов по стольку же. Треугольники бывают всякие: тупоугольные и
равнобедренные, равносторонние и прямоугольные. А есть такие, у которых
все-все углы острые. Они зовутся остроугольными.
Вообще-то, какой треугольник не возьми, в нем три главных отрезка:
медиана, биссектриса, высота. Медиана соединяет вершину треугольника с
серединой стороны, которая лежит напротив. Биссектриса треугольника все
равно, что биссектриса угла, только укороченная. Ну а высота – часть
прямой, перпендикулярной к стороне треугольника, лежащей внутри
треугольника. В прочем и биссектрис, и высот, и медиан в треугольнике по
три. Так что для треугольника число «три» можно назвать магическим».
Как видите, речь семиклассника не отличается красотой и изяществом, а
иногда и содержит математические ошибки. Попробуйте передать его мысли,
не допустив при этом речевых ошибок.
Cлайд №11
Домашнее задание: написать свой рассказ «Что такое треугольник».
П.19,20 №136, 140