Тема урока «ОКРУЖНОСТЬ» (второй урок)

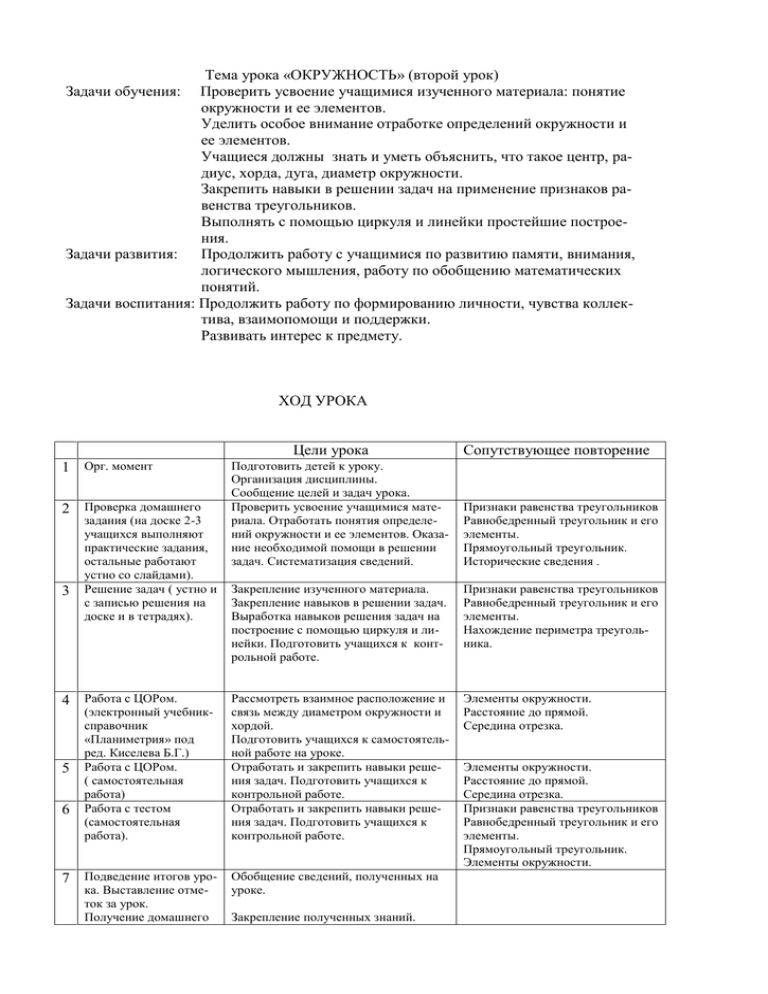
Тема урока «ОКРУЖНОСТЬ» (второй урок)
Задачи обучения: Проверить усвоение учащимися изученного материала: понятие
окружности и ее элементов.
Уделить особое внимание отработке определений окружности и
ее элементов.
Учащиеся должны знать и уметь объяснить, что такое центр, радиус, хорда, дуга, диаметр окружности.
Закрепить навыки в решении задач на применение признаков равенства треугольников.
Выполнять с помощью циркуля и линейки простейшие построения.
Задачи развития:
Продолжить работу с учащимися по развитию памяти, внимания,
логического мышления, работу по обобщению математических
понятий.
Задачи воспитания: Продолжить работу по формированию личности, чувства коллектива, взаимопомощи и поддержки.
Развивать интерес к предмету.
ХОД УРОКА
Цели урока
1 Орг. момент
2 Проверка домашнего
3
задания (на доске 2-3
учащихся выполняют
практические задания,
остальные работают
устно со слайдами).
Решение задач ( устно и
с записью решения на
доске и в тетрадях).
4 Работа с ЦОРом.
5
6
(электронный учебниксправочник
«Планиметрия» под
ред. Киселева Б.Г.)
Работа с ЦОРом.
( самостоятельная
работа)
Работа с тестом
(самостоятельная
работа).
Подготовить детей к уроку.
Организация дисциплины.
Сообщение целей и задач урока.
Проверить усвоение учащимися материала. Отработать понятия определений окружности и ее элементов. Оказание необходимой помощи в решении
задач. Систематизация сведений.
Признаки равенства треугольников
Равнобедренный треугольник и его
элементы.
Прямоугольный треугольник.
Исторические сведения .
Закрепление изученного материала.
Закрепление навыков в решении задач.
Выработка навыков решения задач на
построение с помощью циркуля и линейки. Подготовить учащихся к контрольной работе.
Признаки равенства треугольников
Равнобедренный треугольник и его
элементы.
Нахождение периметра треугольника.
Рассмотреть взаимное расположение и
связь между диаметром окружности и
хордой.
Подготовить учащихся к самостоятельной работе на уроке.
Отработать и закрепить навыки решения задач. Подготовить учащихся к
контрольной работе.
Отработать и закрепить навыки решения задач. Подготовить учащихся к
контрольной работе.
Элементы окружности.
Расстояние до прямой.
Середина отрезка.
7 Подведение итогов уро- Обобщение сведений, полученных на
ка. Выставление отметок за урок.
Получение домашнего
Сопутствующее повторение
уроке.
Закрепление полученных знаний.
Элементы окружности.
Расстояние до прямой.
Середина отрезка.
Признаки равенства треугольников
Равнобедренный треугольник и его
элементы.
Прямоугольный треугольник.
Элементы окружности.
задания.
Во время показа слайдов можно вести беседу и задавать вопросы, например.
Перед первым слайдом: известный математик Гротендик, вспоминая свои школьные годы,
заметил, что увлекся математикой после того, когда узнал определение окружности.
Перед третьим слайдом: древние греки считали окружность самой совершенной фигурой. Почему?
Во время демонстрации 3 слайда: радиус в переводе с латыни обозначает « спица в колесе».
Перед показом второго рисунка в этом слайде: сколько можно провести в окружности радиусов?
После шестого слайда: диаметр с греческого обозначает «поперечник».
Во время демонстрации 7 слайда: как связаны между собой радиус и диаметр одной окружности?
Сколько можно провести диаметров в окружности?
После девятого слайда: каким свойством обладает окружность?
После десятого слайда: каким еще свойством может обладать окружность?
Здесь можно сказать о том, что окружность- это замкнутая кривая линия. Она имеет длину.
Круг - плоская фигура, его характеризует площадь. Можно упомянуть одну из самых знаменитых
задач древности-ЗАДАЧЕ О КВАДРАТУРЕ КРУГА.
ЗАДАЧИ НА ПОСТРОЕНИЕ
1.Начертите прямую а и возьмите на ней две точки А и В, расстояние между которыми равно 7 см.
Постройте окружность (А; 4 см) и окружности (В; 5 см), (В; 3 см), (В; 2 см). Отметьте общие точки
этих окружностей.
2.Начертите три попарно пересекающиеся окружности. Пусть А и В – точки пересечения первой и
второй окружностей, С и D - точки пересечения второй и третьей, а М и N –точки пересечения
первой и третьей окружностей. Проведите прямые АВ, CD, MN.Что можно сказать о точках
пересечения прямых?
3.Начертите окружность и отметьте на ней точку А. Постройте несколько хорд этой окружности,
одним концом которых является точка А. Постройте середины этих хорд. На какой линии они
лежат? Отметьте середины половинок построенных хорд с концом в точке А. Что можно
заметить?
ЗАДАЧИ С ЗАПИСЬЮ РЕШЕНИЯ
Здесь можно решить задачи из «Дидактических материалов по геометрии» под редакцией Б. Г.
Зива. Самостоятельная работа № 11.
УСТНЫЕ ЗАДАЧИ
1.Известно, что для изображения окружности служит циркуль. Гораздо труднее нарисовать
окружность от руки. Предложить учащимся сделать это самим. Можно рассказать о том, что
великий немецкий художник Альбрехт Дюрер одним движением руки мог столь точно
нарисовать окружность, что последующая проверка при помощи циркуля не показывала никаких
отклонений.
Показать правило, позволяющее начертить окружность на клетчатой бумаге от руки: 3-1,1-1,1-3.
Возьмем пересечение линий. Отступив на три клетки вправо и на одну вниз, поставим вторую
точку. Отступая от нее по одной клетке вправо и вниз, находим третью точку. Четвертая точка
находится на расстоянии одной клетки вправо и трех вниз от третьей точки. Соединив плавно
полученные точки, мы изобразим четверть окружности.( Окружность изображается только
определенного размера).
2.Возьмите прямоугольный листок бумаги, который можно накрыть кругом. Перегните листок
(лист перегибается под углом). Можно ли теперь накрыть его тем же кругом?
3.Расположите пять одинакового размера кругов так, чтобы каждый из них касался четырех
остальных.
4.На столе один пятак лежит неподвижно, а другой катится вокруг первого, касаясь его. Сколько
раз он обернется вокруг своего центра, прежде чем вернется в исходное положение?
РАБОТА С ЦОРом
По теме: «Окружность и ее элементы».
Можно предложить учащимся рассмотреть взаимное расположение диаметра и хорды, например:
1.Диаметр перпендикулярен хорде.
2.Диаметр, проходящий через середину хорды.
3.Сравнение диаметра и хорд одной окружности.
4.Две равные хорды.
5.Две неравные хорды.
Затем можно отработать эти свойства окружности при помощи задач, предложенных ЦОРом,
например.
Задача 1. Если АН=6см, то АВ=?
Задача 2. Если у  33 , то х = ?
Задача 3. Если две хорды удалены от центра на расстояние 6см и 8см, то меньшей хордой является
хорда ….
В конце урока учащимся предлагается выполнить тест.