1 - iippk.ru(Главная)

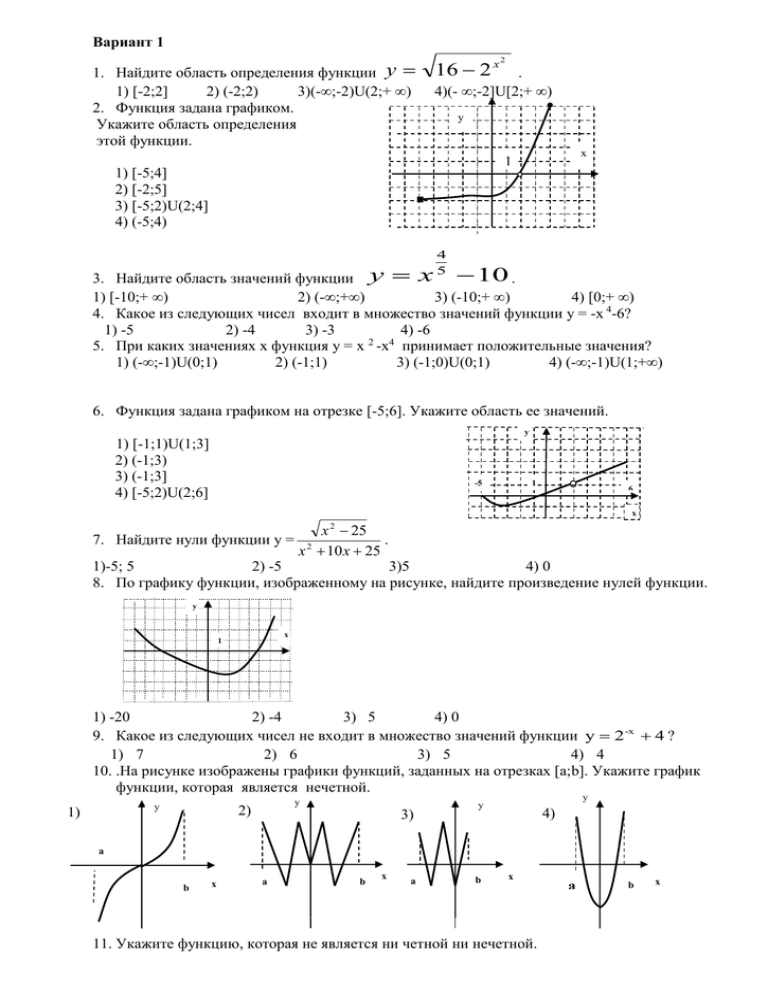
Вариант 1
1. Найдите область определения функции y 
1) [-2;2]
2) (-2;2)
3)(-∞;-2)U(2;+ ∞)
2. Функция задана графиком.
Укажите область определения
этой функции.
16  2 x
2
.
4)(- ∞;-2]U[2;+ ∞)
y
x
1
1) [-5;4]
2) [-2;5]
3) [-5;2)U(2;4]
4) (-5;4)
4
5
3. Найдите область значений функции y  x  10 .
1) [-10;+ ∞)
2) (-∞;+∞)
3) (-10;+ ∞)
4) [0;+ ∞)
4. Какое из следующих чисел входит в множество значений функции у = -x 4-6?
1) -5
2) -4
3) -3
4) -6
2
4
5. При каких значениях х функция у = x -x принимает положительные значения?
1) (-∞;-1)U(0;1)
2) (-1;1)
3) (-1;0)U(0;1)
4) (-∞;-1)U(1;+∞)
6. Функция задана графиком на отрезке [-5;6]. Укажите область ее значений.
у
1) [-1;1)U(1;3]
2) (-1;3)
3) (-1;3]
4) [-5;2)U(2;6]
-5
1
6
x
x  25
.
x  10 x  25
2
7. Найдите нули функции y =
2
1)-5; 5
2) -5
3)5
4) 0
8. По графику функции, изображенному на рисунке, найдите произведение нулей функции.
у
х
1
1) -20
2) -4
3) 5
4) 0
9. Какое из следующих чисел не входит в множество значений функции у  2 -х  4 ?
1) 7
2) 6
3) 5
4) 4
10. .На рисунке изображены графики функций, заданных на отрезках [а;b]. Укажите график
функции, которая является нечетной.
y
1)
y
2)
3)
y
y
4)
a
b
x
a
b
x
a
b
x
11. Укажите функцию, которая не является ни четной ни нечетной.
a
b
x
1) y=cosx
3) y  5 x
2) y=log5x
4)y=х3
12. Найдите точки максимума функции у = -х 3 + 3х 2 .
1) 0
2) 2
3) -2
4) 1/3
13. Функция y  f (x) задана графиком на промежутке  3;5. Укажите промежуток,
которому принадлежат все точки экстремумов.
1) [-3;0]
2) [-2;1]
3) [-1;3]
4) [-1;2]
x
14. По графику производной y=f / (x) функции y =f(x), изображенному на рисунке, укажите
длину промежутка убывания функции y=f(x) на промежутке (-6;4)
у
у = f (x)
1
–6
0
1
4
х
1) 4
2) 6
3) 2
4) 8
15. На рисунке изображен график функции y=f(x).
Пользуясь графиком, найдите все значения аргумента,
при которых функция отрицательна.
1) (-4;0) U (0;3)
3) (-2;0)
2) (-∞;-4) U (3;+∞)
4) (3;+∞)
1
16. Укажите промежуток возрастания функции у = 8х 2 – 8х 3 .
1) [0;2/3]
2) [-2/3;0]
3) (-∞;0]
4) [2/3;+∞)
17. Найдите наибольшее целое значение функции y  сos 2 x  4 cos x  5 .
18. Найдите число целых чисел, принадлежащих интервалам возрастания функции
1
y  2  2  27 х и находящихся на отрезке [-5;5].
x
19. Найдите количество целых чисел, принадлежащих множеству значений функции
y=log 3 (-x2+9).
1
20. Найдите минимум функции y  х  .
х
21. Найдите нули функции y  ( x 2  x  6) 4  8 х  64 .
22. Укажите наименьшее целое число из области определения функции
x 2  12 x  36
y  log 2
x5
x
Вариант 2
1. Найдите область определения функции y= х 2  16
1) [-4;4]
2) (-4;4)
3)(-∞;-4)U(4;+ ∞)
4)(- ∞;-4]U[4;+ ∞)
2. Функция задана графиком.
y
Укажите область определения
этой функции.
1
1) [-3;1]
2) [-5;4]
3) [-5;2)U(2;4]
4) (-3;1)
x
y  5x  7 .
2
3. Найдите область значений функции
1) [8;+ ∞)
2) (8;+∞)
3) (0;+ ∞)
4) [0;+ ∞)
4. Какое из следующих чисел не входит в множество значений функции у = х 4 +8?
1) 9
2) 10
3) 7
4) 8
5. При каких значениях х функция у = х2 +3х-4 принимает положительные значения?
1) (-∞;-4)U(1;+∞)
2) (-4;1)
3) (4;+ ∞)
4) [-4;1]
6. Функция задана графиком. Укажите область ее значений.
у
1) [-1;5)
2) [-5;5)
3) (1;5]
4) [-1;5]
-5
1
5
x
7. Найдите нули функции y = log 2 (x - 7).
1)1,5
2) 2
3)2,5
4) 0
8. По графику функции, изображенному на рисунке, найдите все нули функции.
3
у
х
1
1) -5 ; -1; 5
2) -3; 2
3) 1,5
4) -5 и -1
9. Какое из следующих чисел входит в множество значений функции у  8 х  5 ?
1) 5
2) 6
3) 3
4) 4
10. .На рисунке изображены графики функций. Укажите график функции, которая не
является ни четной, ни нечетной.
1)
y
2)
y
x
11. Укажите четную функцию.
1) y=cosx
2) y=log5x
3)
x
3) y  5 x
y
y
4)
x
4)y=5x
x
12. Найдите точки максимума функции у = х 3 – 3х .
1) -1
2) 1
3) -1; 1
4) 3; 0
13. Функция y  f (x) задана графиком на промежутке  3;5. Укажите промежуток,
которому принадлежат все точки экстремумов.
1) [-3;0]
2) [-2;1]
3) [-1;1]
4) [-1;4]
x
14. По графику производной y=f / (x) функции y =f(x), изображенному на рисунке, укажите
точку максимума функции y=f(x) на промежутке (-6;4)
у
у = f (x)
1
–6
0
1
х
4
1) -4
2) -2
3) 2
4) -1
15. На рисунке изображен график функции y=f(x).
Пользуясь графиком, найдите все значения аргумента,
при которых функция положительна.
1) (-3;0) U (0;+∞)
3) (-3;0)
1
2) (-∞;-3) U (-3;+∞)
4) (-3;+∞)
x
16. Укажите промежуток возрастания функции у = х 3 –3 х .
1) (-∞;-1] U [1;+∞)
2) [-1;1]
3) (-1;1)
4) [1;+∞)
cos 4 x cos 3 x sin 4 x sin 3 x
17. Найдите наибольшее целое значение функции y  25  3
5.
5x
18. Найдите длину промежутка возрастания функции y  2
.
x 1
19. Найдите количество целых чисел, принадлежащих множеству значений функции
y  4 sin x  2 .
20. Укажите длину промежутка области определения функции y  log 0,5 ( x  1)
21. Найдите сумму нулей функции y  ( x 2  5 x  4)  4  0,5  x .
3 x  3 x 1
y
x
2
22. Найдите нули функции
.
Вариант 3
1. Найдите область определения функции y=log
1) [0;1]
2) (0;1)
3)(-∞;0)U(1;+ ∞)
2. Функция задана графиком.
Укажите область определения
этой функции.
x - x2 ).
4)(- ∞;0]U[1;+ ∞)
0,2 (
y
x
1
1) [-5;4]
2) [-2;5]
3) [-5;2)U(2;4]
4) (-5;4)
x 2 1
3. Найдите область значений функции y  5
.
1) [5;+ ∞)
2) (-∞;+∞)
3) (0;+ ∞)
4) [0;+ ∞)
4. Какое из следующих чисел не входит в множество значений функции у = х 2 +4?
1) 5
2) 7
3) 3
4) 4
5. При каких значениях х функция у = х2(х-8)3 принимает положительные значения?
1) (-∞;0)U(8;+∞)
2) (0;8)
3) (8;+ ∞)
4) (-∞;8)
6. Функция задана графиком на отрезке [-5;6]. Укажите область ее значений.
у
1) [2;5]
2) (2;5)
3) (1;5]
4) [1;5]
-5
1
6
7. Найдите нули функции y = log 2 (2x – 3).
1)1,5
2) 2
3)2,5
4) 0
8. По графику функции, изображенному на рисунке, найдите все нули функции.
x
у
х
1
1) -2 и 4
2) -2 и 0
3) -1 и 4
4) -2 и -1
х
9. Какое из следующих чисел входит в множество значений функции у  2  4 ?
1) 5
2) 2
3) 3
4) 4
10. .На рисунке изображены графики функций, заданных на отрезках [а;b]. Укажите график
функции, которая не является ни четной, ни нечетной.
y
1)
a
y
2)
3)
y
y
4)
b
x
a
b
x
a
b
x
a
b
x
11. Укажите нечетную функцию.
1) y=cosx
2) y=log5x
3) y  5 x
4)y=5x
12. Найдите точки максимума функции у = х 3 – 3х 2.
1) 0
2) 2
3) -2
4) 1/3
13. Функция y  f (x) задана графиком на промежутке  3;5. Укажите промежуток,
которому принадлежат все точки экстремумов.
1) [-3;0]
2) [-2;1]
3) [-1;1]
4) [-1;2]
x
14. По графику производной y=f / (x) функции y =f(x), изображенному на рисунке, укажите
точку минимума функции y=f(x) на промежутке (-6;4)
у
у = f (x)
1
–6
0
1
4
х
1) -4
2) -2
3) 2
4) -1
15. На рисунке изображен график функции y=f(x).
Пользуясь графиком, найдите все значения аргумента,
при которых функция положительна.
1) (-3;0) U (3;+∞)
3) (0;3)
1
2) (-∞;-2) U (1;+∞)
4) (3;+∞)
x
16. Укажите промежуток возрастания функции у = х 2 – х 3 .
1) [0;2/3]
2) [-2/3;0]
3) (-∞;0]
4) [2/3;+∞)
cos 4 x cos 3 x  sin 4 x sin 3 x  2
17. Найдите наибольшее целое значение функции y  25  3
.
18. Найдите число целых чисел, принадлежащих интервалам возрастания функции
216
y  2x3 
и находящихся на отрезке [-5;5].
x
19. Найдите количество целых чисел, принадлежащих множеству значений функции
10
y 2
1 .
x 5
x3 x2
1

 6 x  25 .
20. Найдите минимум функции y 
3
2
2
21. Найдите сумму нулей функции y  ( x 2  x  6) 
x2 1
.
2x
22. Найдите нули функции y  ln 2 ( x 2  3x  9)  x 3  8 x  8 .