МНК. Корреляционный и регрессионный анализ

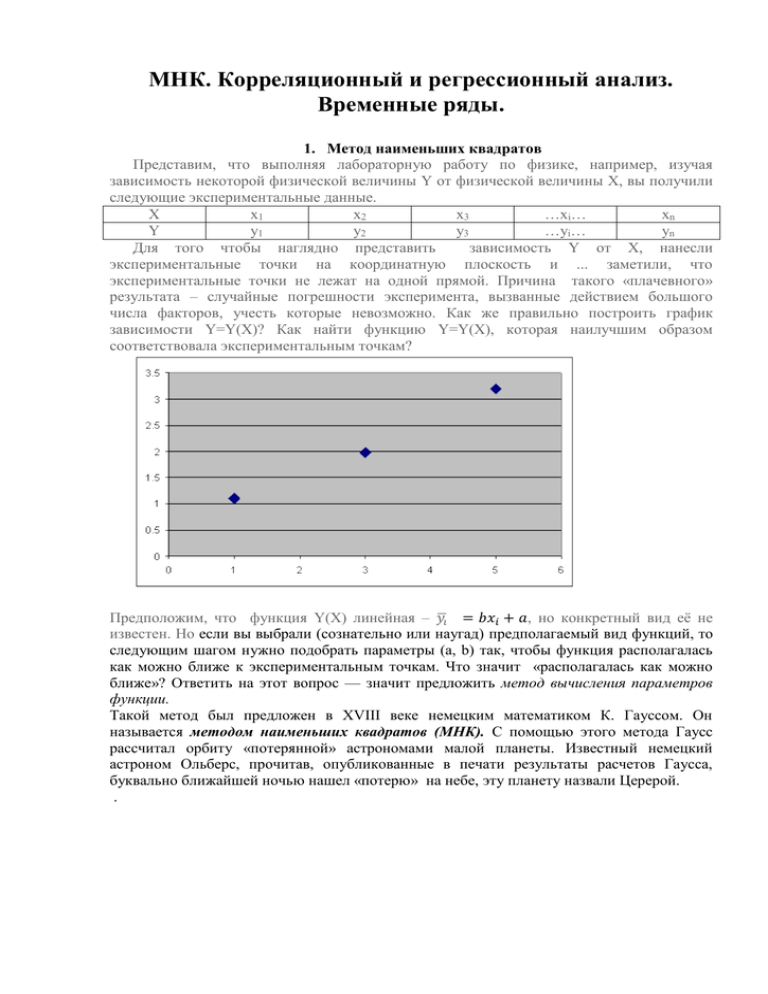
МНК. Корреляционный и регрессионный анализ.
Временные ряды.
1. Метод наименьших квадратов
Представим, что выполняя лабораторную работу по физике, например, изучая
зависимость некоторой физической величины Y от физической величины X, вы получили
следующие экспериментальные данные.
X
x1
x2
x3
…xi…
xn
Y
y1
y2
y3
…yi…
yn
Для того чтобы наглядно представить
зависимость Y от X, нанесли
экспериментальные точки на координатную плоскость и ... заметили, что
экспериментальные точки не лежат на одной прямой. Причина такого «плачевного»
результата – случайные погрешности эксперимента, вызванные действием большого
числа факторов, учесть которые невозможно. Как же правильно построить график
зависимости Y=Y(X)? Как найти функцию Y=Y(X), которая наилучшим образом
соответствовала экспериментальным точкам?
Предположим, что функция Y(Х) линейная – 𝑦̅𝑖 = 𝑏𝑥𝑖 + 𝑎, но конкретный вид её не
известен. Но если вы выбрали (сознательно или наугад) предполагаемый вид функций, то
следующим шагом нужно подобрать параметры (а, b) так, чтобы функция располагалась
как можно ближе к экспериментальным точкам. Что значит «располагалась как можно
ближе»? Ответить на этот вопрос — значит предложить метод вычисления параметров
функции.
Такой метод был предложен в XVIII веке немецким математиком К. Гауссом. Он
называется методом наименьших квадратов (МНК). С помощью этого метода Гаусс
рассчитал орбиту «потерянной» астрономами малой планеты. Известный немецкий
астроном Ольберс, прочитав, опубликованные в печати результаты расчетов Гаусса,
буквально ближайшей ночью нашел «потерю» на небе, эту планету назвали Церерой.
.
Иоганн Карл Фри́дрих Га́усс (нем. Johann Carl Friedrich Gauß; 30 апреля 1777, Брауншвейг — 23
февраля 1855, Гёттинген) — немецкий математик, астроном и физик, считается одним из
величайших математиков всех времён, «королём математиков».
Суть метода наименьших квадратов (МНК) заключается в следующем:
искомая функция должна быть построена так, чтобы сумма квадратов отклонений
уi - ординат всех экспериментальных точек от 𝑦̅𝑖 = 𝑏𝑥𝑖 + 𝑎 - ординат графика
функции была бы минимальной.
Иными словами нужно свести к минимуму функцию S:
S= ∑𝑛𝑖=1(𝑦̅𝑖 – 𝑦𝑖 )2 = ∑𝑛𝑖=1(𝑎 + 𝑏𝑥𝑖 – 𝑦𝑖 )2 → 𝑚𝑖𝑛
Может возникнуть вопрос, а именно почему сумма квадратов? Дело в том, что, во-первых,
квадрат любого числа всегда неотрицателен, и, следовательно, сумма квадратов всегда не
отрицательна, т.е. ограничена снизу, и, следовательно, у нее есть минимум.
Ведь иметь в двух точках отклонение в 5 единиц, лучше, чем в первой точке иметь
нулевое отклонение, зато во второй точке иметь отклонение 10. Сумма отклонений в
обоих случаях будет одинаковой, а вот сумма квадратов отклонений в первом случае
будет меньше.
Для отыскания минимума функции S приравняем нулю соответствующие частные
производные:
.
Выполнив элементарные преобразования, получим систему двух линейных уравнений
относительно а и b:
Решения этой системы уравнений можно записать в следующем, удобном для расчетов
виде:
(1)
Получив значения a и b, можно составить уравнение линейной зависимости вида
𝑦̅ = 𝑎𝑥𝑖 + 𝑏 и построить график этой зависимости:
Как видно из рисунка, прямая довольно неплохо вписывается в набор экспериментальных
точек.
Данные рисунки получены с помощью MS Excel. Полученный график называется
трендом. Английское слово trend можно перевести как общее направление, или тенденция.
(Кстати, обычно b называют коэффициентом регрессии. Коэффициент регрессии
показывает, на сколько единиц в среднем изменяется переменная Y при увеличении
переменной Х на одну единицу.)
Пример. Построить график зависимости по данным n=8 наблюдений, которые получены
при изучении зависимости количества продаж лекарственного средства «Амбробене» у от
затрат на рекламу этого товара х( в млн. руб):
х 1,5
4,0
5,0
7,0
8,5
10,0
11,0
12,5
y 5,0
4,5
7,0
6,5
9,5
9,0
11,0
9,0
Решение. Экспериментальные данные изобразим в виде точек на координатной плоскости.
Соединим полученные точки. По виду ломанной можно предположить наличие линейной
зависимости между двумя рассматриваемыми переменными, которая графически
выражается
тем
точнее,
чем
больше
объем
выборки
Для построения линии тренда составим расчетную таблицу:
№
хi
yi
x i2
xiyi
1
1,5
5,0
2,25
7,50
2
4,0
4,5
16,00
18,00
3
5,0
7,0
25,00
35,00
4
7,0
6,5
49,00
45,50
5
8,5
9,5
72,25
80,75
6
10,0
9,0
100,00
90,00
7
11,0
11,0
121,00
121,00
8
12,5
9,0
156,25
112,50
Σ
59,5
61,5
541,75
510,25
Найдем искомые параметры, для чего подставим вычисленные по таблице суммы в
соотношения (1):
а = (61,5 × 541,75 – 510,25 ×59,50)/ (8 ×541,75 – 3540,25) = 3,73,
b = (8 × 510,25 – 59,50 × 61,50)/ (8 ×541,75 – 3540,25) = 0,53.
Таким образом, уравнение тренда имеет вид
.𝑦̅ = 3,73 + 0,53𝑥
Построенная линия тренда позволяет с некоторой вероятностью не только предсказать в
интервале от х=1,5 до х=12,5 любые значения функции у при отсутствующих в таблице
значениях фактора х, но и за пределами данного интервала.
МНК и поиск по картинкам, лицам и картам
Этот метод можно применить и в поиске по картинкам, чертежам, картам и даже по лицам
людей.
Поиск по лицам, заснятым на камеру наблюдения
Сейчас все поисковики, вместо поиска по картинкам, используют поиск по подписям к
картинкам. Это, несомненно, полезный и удобный сервис, но его можно дополнить
настоящим поиском по картинкам. Вводится картинка-образец, и для всех изображений
составляется рейтинг по сумме квадратов отклонений характерных точек. Определение
этих самых характерных точек есть сама по себе нетривиальная задача. Однако она
вполне решаема: например, для лиц это уголки глаз, губ, кончик носа, ноздри, края и
центры бровей, зрачки и т.д. Сопоставив эти параметры, можно найти лицо, наиболее
похожее на образец. Есть сайты, где такой сервис работает, и вы можете найти
знаменитость, наиболее похожую на предложенную вами фотографию и даже составить
анимацию, превращающую вас в знаменитость и обратно. Наверняка, этот же метод
работает в базах МВД, содержащих фотороботы преступников.
2. Статистический анализ временных рядов.
Временно́й ряд (или ряд динамики) — это собранные в разные моменты
времени значения случайной величины, характеризующие исследуемый процесс. Во
временном ряде каждому значению случайной величины должно быть указано время
измерения или номер измерения по порядку. Временной ряд существенно отличается от
простой выборки данных, так как при анализе учитывается взаимосвязь измерений со
временем, а не только статистическое разнообразие и статистические характеристики
выборки. Временные ряды, как правило, возникают в результате измерения технических,
природных, социальных, экономических характеристик различных систем (например,
погодные данные). Типичным примером временного ряда можно назвать биржевой курс,
при анализе которого пытаются определить основное направление развития (тенденцию
или тренд).
Временные ряды состоят из двух элементов:
 периода времени, за который или по состоянию на который приводятся числовые
значения;
 числовых значений той или иной случайной величины.
Временные ряды по своему представлению бывают дискретные и непрерывные.
Дискретный ряд получают при последовательных наблюдениях значений случайной
величины через равные промежутки времени (например, через 1с или 1 час).
Пример дискретного временного ряда: результаты измерений в ходе лечения утренней
температуры тела пациента.
Непрерывный ряд
величиной.
представляет результаты непрерывных наблюдений за случайной
Пример. Результаты снятия ЭКГ.
Анализируются обычно дискретные временные ряды, т.е. непрерывный ряд
представляется в виде дискретного.
 Временные ряды бывают детерминированными и случайными (стохастическими):
первые (встречаются крайне редко) получают, если существует строгое
соответствие (однозначная зависимость) между значениями времени регистрации
и
соответствующими
значениями
временного
ряда
(например,
ряд
последовательных данных о количестве дней в месяцах); вторые, которые реально
встречаются, есть результат реализации некоторой случайной величины (число
студентов на лекциях).
 Различают стационарные и нестационарные временные ряды. Стационарным
временным рядом называют ряд, функция распределения значений которого не
зависит от времени (средние значения и дисперсии постоянны, пример количество всё тех же студентов на лекциях). Нестационарным рядом называют
ряд, функция распределения которого меняется со временем.
Стационарные временные ряды характеризуются на основе анализа результатов
вычислений математического ожидания, дисперсии и среденеквадратичного
отклонения.
Нестационарный временной ряд может быт представлен в виде двух составляющих:
детерминированной компоненты
f(t) (тренда)
и случайной компоненты Ɛ(t).
Пример графического изображения нестационарного временного ряда.
Детерминированная компонента изображена синей линией.
Детерминированная компонента f(t) (тренд) – характеризует основную тенденцию
изменения временного ряда с течением времени, на которую накладываются случайные
отклонения , определяемые компонентой Ɛ(t) ( "шумы", случайные погрешности).
То есть исходный временной ряд X(t) представляется в виде суммы:
X(t) = f(t) + Ɛ(t)
На практике наибольший интерес представляет выявления основной тенденции изменения
временного ряда. Одним из методов нахождения уравнения тренда является метод
наименьших квадратов.
Статистические модели на основе изучения нестационарных временных рядов служат для
описания вероятные значения временного ряда в ближайшем будущем при известных
последних значениях (прогноз). Прогноз будущих значений временного ряда
используется для эффективного принятия решений.
Пример. Движение цен на валютном рынке происходит в соответствии с определёнными
тенденциями - трендами. Рост курса происходит, когда спрос на определенную валюту
превышает предложение на рынке, и наоборот. При долгосрочном росте или падении
курса валют, участники рынка говорят о том, что сложился "восходящий" (рост курса),
либо "нисходящий" (падение курса) тренд по данной валюте. Также, выделяют иногда
третий тип тренда - "боковой", хотя, по сути, это, как раз, отсутствие тренда - ярко
выраженного роста или падения курса валюты в течение определённого периода времени.
Неформально, восходящий тренд участники рынка называют "бычьим", а нисходящий
"медвежьим". Боковой тренд называют просто - "флэт" (от англ. flat - плоский). На
основании анализа трендов ( или вопреки ему) принимается решение о покупке валюты.
Восходящий и нисходящие тренды.
Боковой тренд.
3. Корреляционный и регрессионный анализы.
Основные понятия:
3.1. Статистическая зависимость ее отличие от функциональной зависимости.
В медико-биологических исследованиях в большинстве случаев между
переменными величинами существуют зависимости такого вида, когда каждому значению
одной переменной (Х) соответствует не какое-то одно определенное, а множество
значений другой переменной(Y), причем нельзя сказать заранее, какое именно значение
примет зависимая величина Y. Такая зависимость получила название статистической (или
стохастической, вероятностной). Наиболее часто появление такой зависимости
объясняется действием на результирующую переменную не только контролируемого
фактора или контролируемых факторов (в данном случае таким контролируемым
фактором является переменная Х), а и многочисленных неконтролируемых случайных
факторов:
X
Y1, Y2, … ,Yn
Например, если Х- количество вводимого объекту препарата, то его концентрация в крови
Y в произвольный момент времени статистически зависит от величины Х, т.к.
определяется не только количеством вводимого препарата, но и многими другими
случайными факторами (масса тела пациента, скорость выведения вещества из организма,
и т.д.)
Простейшим визуальным способом выявить наличие взаимосвязи между
количественными переменными является построение диаграммы рассеяния (scatterplot).
Это график, на котором по горизонтальной оси (X) откладывается одна переменная, по
вертикальной (Y) другая. Каждому объекту на диаграмме соответствует точка, координаты
которой равняются значениям пары выбранных для анализа переменных.
Пример. Диаграмма рассеяния (scatterplot), представляющая зависимость между
численностью рабочих на фармацевтическом предприятии и доходом предприятий
(при одной и той же численности персонала прибыльность предприятий различна)
Понять особенность статистической зависимости проще, если сравнить её с хорошо
знакомой из курса математики функциональной зависимостью – зависимостью вида,
когда каждому возможному значению случайной величины Х соответствует одно
возможное значение случайной величины Y . Например, длина окружности связана с
радиусом окружности функциональной зависимостью вида Y=2πX.
X
Y
В простейшем случае линейной зависимости, чем больше значения одного признака, тем
больше значения другого, и чем меньше значения одного признака, тем меньше значения
другого.
График, представляющий линейную функциональную зависимость.
3.2. Корреляционная зависимость:
Линии регрессии.
Допустим, что существует стохастическая зависимость случайной переменной Y от
Х. Зафиксируем некоторое значение х переменной Х. Переменная Y, в силу ее случайной
зависимости от Х, может принять любое значение из некоторого множества, причем какое
именно – заранее не известно. Поэтому, прежде всего, стараются выяснить, изменяется
или нет при изменении Х математическое ожидание Y.
X
𝑌
Если при изменении X математические ожидания М(Y) изменяются, то говорят, что имеет
место корреляционная1 зависимость величины Y от Х.
Примерами
корреляционных
зависимостей
являются
рассмотренная
выше
статистическая зависимость между дозой лекарственного препарата и его
содержанием в крови, зависимость между ростом человека и его массой, порядковым
номером рождения и мотивацией достижений.
Интересно, существует ли корреляционная зависимость между массой человека и его
IQ?
Функция же f(х)=М(Y), описывающая изменение математического ожидания
случайной переменной Y при изменении значений переменной Х, называется функцией
регрессии Y на Х, а ее график – линией регрессии.
Термин «регрессия» ввёл в математическую статистику Френсис Гальтон.
Гальтон был двоюродным братом Чарльза Дарвина по их деду — Эразмусу (Эразму)
Дарвину. Семья Гальтон была известной и весьма успешной в сфере изготовления
оружия и банкирском деле, в то время как Дарвины отличались в медицине и науке. После
выхода книги Происхождение видов своего двоюродного брата Чарльза Дарвина Френсис
Гальтон стал биологом. В 1869 вышла книга «Наследственный гений» — венец научной
работы Гальтона (В книге проанализирован обширный материал по «выдающимся
людям». В рассуждениях он подошел к пониманию феномена нормального распределения
признаков в человеческой популяции).
Сэр Фрэнсис Гальтон (англ. Francis Galton; 16 февраля 1822 — 17 января 1911) —
английский исследователь, географ, антрополог и психолог; основатель
дифференциальной психологии и психометрики.
Статистическое использование слова «регрессия» исходит из явления, известного как
регрессия к среднему. Гальтон показал, что, хотя высокие отцы имеют тенденцию
иметь высоких сыновей, средний рост сыновей меньше, чем у высоких отцов. Средний
1
КОРРЕЛЯЦИЯ (от
позднелат. сorrelatio — соотношение) — взаимная связь, связь
(согласованность), свойств, черт, показателей.
как синхронность
рост сыновей «регрессировал» или «двигался вспять» к среднему росту всех отцов в
популяции.
Если f(х) – линейная функция, то корреляционную зависимость можно описать с
помощью уравнения вида
М(Y/х) =Bх+A,
(2)
где А и В – некоторые параметры, а М(Y/х) – условное математическое ожидание
наблюдавшихся значений Y, соответствующих Х=х.
Пусть в нашем распоряжении имеется лишь выборка ограниченного объема. Поэтому в
этом случае речь может идти об оценке (приближенном выражении) функции регрессии.
В качестве оценок математических ожиданий принимают условные средние, которые
находят по данным наблюдений (по выборке). Условным средним ух называют среднее
арифметическое наблюдавшихся значений Y, соответствующих Х=х.
Условное математическое ожидание М(Y/х) является функцией от х, следовательно, его
оценка, т.е. условное среднее ух, также функция от х; обозначив эту функцию через φ (х),
получим уравнение ух = φ(х). Это уравнение называют выборочным уравнением
регрессии; функцию φ (х) называют выборочной регрессией, а ее график – выборочной
линией регрессии.
Поскольку наиболее простой формой зависимости в математике является прямая, то в
корреляционном и регрессионном анализе наиболее популярны линейные модели. Если
функция φ(х) линейная, то выборочное уравнение линейной регрессии Y на Х имеет вид:
yx=𝞺xy x + a (по аналогии с уравнением (2)),
где 𝞺xy – выборочный коэффициент линейной регрессии Y на X, . yx – условное среднее
значение y для соответствующих Х=х.
Попробуем провести линию регрессии через облако точек на диаграмме рассеяния.
Диаграмма связи между численностью рабочих на фармацевтическом предприятии
и доходом предприятия.
Таких линий можно нарисовать множество, причем на глаз невозможно определить, какая
из них лучше подходит для описания диаграммы рассеяния?
Вы уже знакомы с методом, который позволяет совершенно точно вычислить положение
прямой линии, наилучшим образом проходящей через облако точек, и составить
уравнение этой линии. Это – метод наименьших квадратов. Вычисляемая с его помощью
прямая линия – линия регрессии. Она характеризуется тем, что сумма квадратов
расстояний от точек на диаграмме до этой линии минимальна (по сравнению со всеми
возможными линиями). Таким образом, линия регрессии дает наилучшее приближенное
описание линейной зависимости между двумя переменными.
Смысл коэффициента регрессии 𝞺xy
1) В общем случае коэффициент регрессии показывает, как в среднем изменится
значение Y, если X увеличится на единицу.
2) Численно он равен тангенсу угла между прямой линией регрессии Y на X и
положительным направлением оси ОХ.
3) По величине коэффициента регрессии судят о силе корреляционной связи между
изучаемыми величинами: чем больше величина 𝞺xy, тем сильнее изменится среднее
значение Y при изменении Х, тем сильнее корреляционная связь.
Пример уравнения регрессии:
• На диаграмме рассеяния показаны не только точки-объекты и теоретическая линия
регрессии, но и может быть записано уравнение этой (прямой) линии:
Y = 87610 + 2984 X
Пример интерпретации коэффициента регрессии:
• В уравнении Y = 87610 + 2984 X
коэффициент регрессии равен +2984. Что это означает?
• В данном случае смысл коэффициента регрессии состоит в том, что увеличение числа
рабочих на фармацевтическом предприятии на 1 чел. приводит в среднем к увеличению
объема годового производства на 2984 руб.
Какова бы ни была конфигурация облака точек на диаграмме рассеяния – лежат ли они в
точности на одной прямой, или разбросаны хаотически – любая статистическая
компьютерная программа всегда сможет построить уравнение регрессии. Может
оказаться, что через два облака, различающихся степенью близости к линейной
конфигурации, будут проведены одинаковые линии регрессии. Однако в одном случае
точки могут лежать на одной прямой, а в другом случае – нет.
То есть зависимость между двумя переменными может иметь различный характер даже
при одинаковых линиях регрессии.
Оказывается форма связи (линия регрессии) сама по себе не дает ответа на вопрос о
тесноте связи пары переменных. На этот вопрос отвечает коэффициент парной
корреляции. Он показывает, насколько тесно две переменные связаны между собой.
Визуально о тесноте связи можно судить по тому, насколько компактно расположены
точки-объекты около линии регрессии. Чем ближе точки к линии регрессии, тем теснее
связь.
Пример. На каком из двух графиков связь между признаками сильнее (теснее), т.е. какому
из графиков соответствует более высокий коэффициент корреляции, характеризующий
степень зависимости двух переменных?
Коэффициент парной корреляции r принимает значения в диапазоне от –1 до +1.
Положительные значения коэффициента корреляции r свидетельствуют о положительной
связи между признаками, отрицательные – об отрицательной связи.
Если r = 1, то между двумя переменными существует функциональная положительная
линейная связь, т.е. на диаграмме рассеяния соответствующие точки лежат на одной
прямой с положительным наклоном.
Если r = –1, то между двумя переменными существует функциональная отрицательная
линейная зависимость, т.е. на диаграмме рассеяния соответствующие точки лежат на
одной прямой с отрицательным наклоном.
Если r = 0, то рассматриваемые переменные линейно независимы, т.е. на диаграмме
рассеяния облако точек "вытянуто по горизонтали".
Формула для вычисления парного коэффициента корреляции:
Чем выше по модулю (по абсолютной величине) значение коэффициента
корреляции, тем сильнее связь между признаками. Принято считать, что коэффициенты
корреляции, которые по модулю больше 0,7, говорят о сильной связи Коэффициенты
корреляции, которые по модулю меньше 0,7, но больше 0,5, говорят о связи средней силы.
Наконец, коэффициенты корреляции, которые по модулю меньше 0,5, говорят о слабой
связи.
Сравнение коэффициентов корреляции и регрессии
Коэффициент корреляции
• Принимает значения в диапазоне от -1 до +1
• Безразмерная величина
• Показывает тесноту связи (связь как синхронность, согласованность) между
признаками
• Знак коэффициента говорит о направлении связи
Коэффициент регрессии
• Может принимать любые значения
• Привязан к единицам измерения обоих признаков
• Показывает структуру связи между признаками: характеризует связь как зависимость,
влияние, устанавливает причинно-следственные связи.
• Знак коэффициента говорит о направлении связи
Усложнение модели
• Совокупное влияние всех независимых факторов на зависимую переменную не может
быть представлено как простая сумма нескольких парных регрессий.
• Это совокупное влияние находится более сложным методом - методом множественной
регрессии .
Визуализация модели множественной регрессии
Этапы проведения корреляционного и регрессионного анализа:



Выявление наличия взаимосвязи между признаками;
Определение формы связи;
Определение силы, тесноты и направления связи.