68 КБ

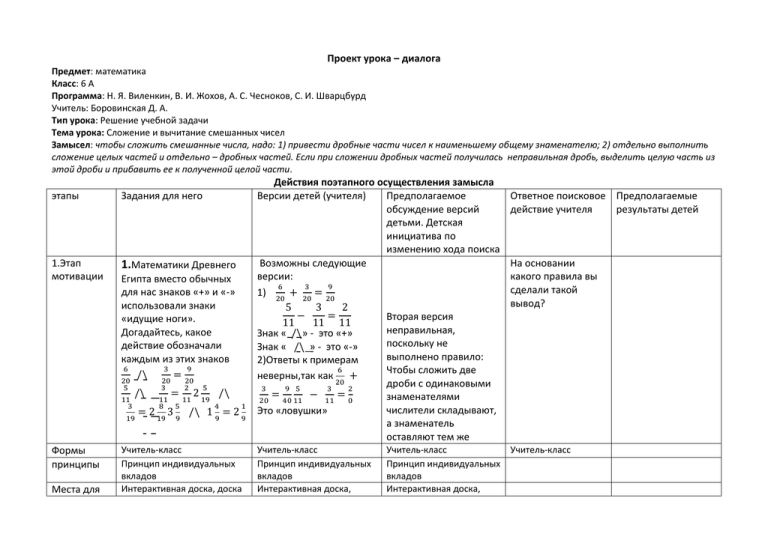
Проект урока – диалога
Предмет: математика
Класс: 6 А
Программа: Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд
Учитель: Боровинская Д. А.
Тип урока: Решение учебной задачи
Тема урока: Сложение и вычитание смешанных чисел
Замысел: чтобы сложить смешанные числа, надо: 1) привести дробные части чисел к наименьшему общему знаменателю; 2) отдельно выполнить
сложение целых частей и отдельно – дробных частей. Если при сложении дробных частей получилась неправильная дробь, выделить целую часть из
этой дроби и прибавить ее к полученной целой части.
этапы
Задания для него
1.Этап
мотивации
1.Математики Древнего
Египта вместо обычных
для нас знаков «+» и «-»
использовали знаки
«идущие ноги».
Догадайтесь, какое
действие обозначали
каждым из этих знаков
6
3
9
/\
=
20
20
20
5
11
3
/\
19
Формы
принципы
Места для
3
=
2
11
11
8
5
2
5
19
/\
4
1
= 2 19 3 9 /\ 1 9 = 2 9
Учитель-класс
Принцип индивидуальных
вкладов
Интерактивная доска, доска
Действия поэтапного осуществления замысла
Версии детей (учителя)
Предполагаемое
обсуждение версий
детьми. Детская
инициатива по
изменению хода поиска
Возможны следующие
версии:
6
3
9
1) 20 + 20 = 20
5
3
2
−
=
Вторая версия
11
11 11
неправильная,
Знак « /\» - это «+»
поскольку не
Знак « /\ » - это «-»
выполнено правило:
2)Ответы к примерам
6
Чтобы сложить две
неверны,так как 20 +
дроби с одинаковыми
3
9 5
3
2
=
−
=
знаменателями
20
40 11
11
0
числители складывают,
Это «ловушки»
а знаменатель
оставляют тем же
Учитель-класс
Принцип индивидуальных
вкладов
Интерактивная доска,
Ответное поисковое Предполагаемые
действие учителя
результаты детей
На основании
какого правила вы
сделали такой
вывод?
Учитель-класс
Учитель-класс
Принцип индивидуальных
вкладов
Интерактивная доска,
доска
работы
доска
этапы
Задания для него
Версии детей (учителя)
1. этап
мотивации
1 29
2
2. вместо квадратиков 1) 31
= 65 3 = 93
5
назовите числа, чтобы
равенства оказались
31
верными 5 =
1 29
5 3
=93
2
= 15
3. Вычислить
2
5
1 29
= 35
5
6
5
2
= 93
12
2
=1
5
5
3
3
+4=
7
3
10+9
12
5+3
19
= 12 ==
8
+ 4 = 6+4 = 10
1
6
7
2 +4 =6 =7
7
7
7
2
2
4
1
1 +2 =3 =3+1
3
3
3
3
1
=4
3
14 2
12
4
2 −
=2
=2
15 15
15
5
2)
1
2
31
1 12
4. вычислить 2 7 +
6
2)
1)
5 3
+
6 4
4713 + 23
14 2
2 −
15 15
7
2
=1
5
5
6
2. поста- Посмотрите на
следующие примеры.
новка
учебной 16 3 + 19 1 5 7 − 2 1
8
4
9
6 Нет
задачи
5
3
4
5
5 +3
3 −1
6
4
9
6 В дробных частях разные
Предполагаемое обсуждение
версий детьми. Детская инициатива
по изменению хода поиска
Ответное
поисковое
действие учителя
Чтобы выделить целую часть из
неправильной дроби, нужно
разделить с остатком числитель на
знаменатель. Неполное частное это
целая часть, а остаток дает
числитель. Поэтому 2 версия
неверна
Какое правило
использовали?
Вторая версия неверна.
Чтобы сложить дроби с разными
знаменателями, надо привести их к
НОЗ и сложить полученные дроби.
Чтобы сложить (вычесть)
смешанные числа целые части
складывают (вычитают) отдельно, а
дробные – отдельно.
Почему получили
разные ответы?
Предполагае
мые
результаты
детей
Какое правило
использовали?
Сможете ли вы
сразу дать на них
ответ?
Почему?
Так какой вопрос
мы будем
Как сложить
и вычесть
смешанные
числа с
разными
4−
этапы
5
8
знаменатели
Задания для него
3 этап
Для начала в группах
Модели- решите примеры со
рование сложением
3
1 5
3
16 + 19
5 +3
8
4
6
4
рассматривать на
уроке?
Версии детей (учителя)
Возможны версии:
5
3
8
1) 5 6 + 3 4=8 10
2)
3
1
3
2
16 8 + 19 4 =16 8 + 19 8 =
5
= 35 8
5
3
10
9
5 6 + 3 4=5 12 + 3 12 =
19
7
8 12 = 9 12
4. этап
рефлексии
(работа
в парах)
Решите примеры и
узнайте средство, которое
использовали для чистки
зубов в XVIII веке
1
5
1 +3 =
6
5
18
5
5
7
9 6 + 2 9=
67 + 2 8
2
3
5 3 + 4=
4
1
Ключ: 4 9 = с; 3 2 =
33
к; 9 56 = л;
соль
Предполагаемое
обсуждение версий
детьми. Детская
инициатива по
изменению хода поиска
Первую версию
опровергают правилом
сложения дробей с
одинаковыми
знаменателями
На доске выписывают
разные решения
Ответное поисковое
действие учителя
знаменателя
ми в дробных
частях?
Предполагаемые
результаты детей
Сформулируйте сами Чтобы сложить два
ответ на вопрос
смешанных числа,
урока
надо 1) привести
дроби к НОЗ
2)отдельно сложить
дробные, отдельно –
целые части 3) если
получилась
неправильная дробь,
выделить целую часть
11
7
− ю; 2
= о;
23
18
5
1
6
= ь; 5 = д
12
2
Задания для него
7 = а; 6
этапы
4. этап
рефлексии
Версии детей (учителя)
На слайде:
Желающим предлагается
творческое домашнее
задание (представлено
ниже)
форма
Ученик-ученик
Ученик-ученик
принцип Принцип индивидуальных Принцип индивидуальных
вкладов
вкладов
Места
для
работы
Предполагаемое
обсуждение версий
детьми. Детская
инициатива по
изменению хода поиска
Тетрадь, доска, карточки
Тетрадь, доска
Домашнее задание: Вставь пропущенные числа
Ответное поисковое
действие учителя
Подведем итоги.
Поднимите
улыбающуюся
рожицу те, у кого
были лишь
незначительные
трудности. А
грустную рожицу
поднимут те, кто не
совсем разобрался в
вопросе урока.
Ученик-ученик
Принцип
индивидуальных
вкладов
Тетрадь, доска
Предполагаемые
результаты детей
1
5
5
1) 91 6 + 3 18 = 91 18 + 3 18 = 9
3
16
2) 1 15 + 2 20 = 1 60 + 2 60 =
18
=
= 99
3)8+5 = 11
5
12
7
2
4) 67 + 2 8 = 6
+2
=8
=9