ВОПРОС, ЗАДАНИЕ 1 2 3 1 Любой вектор можно разложить по

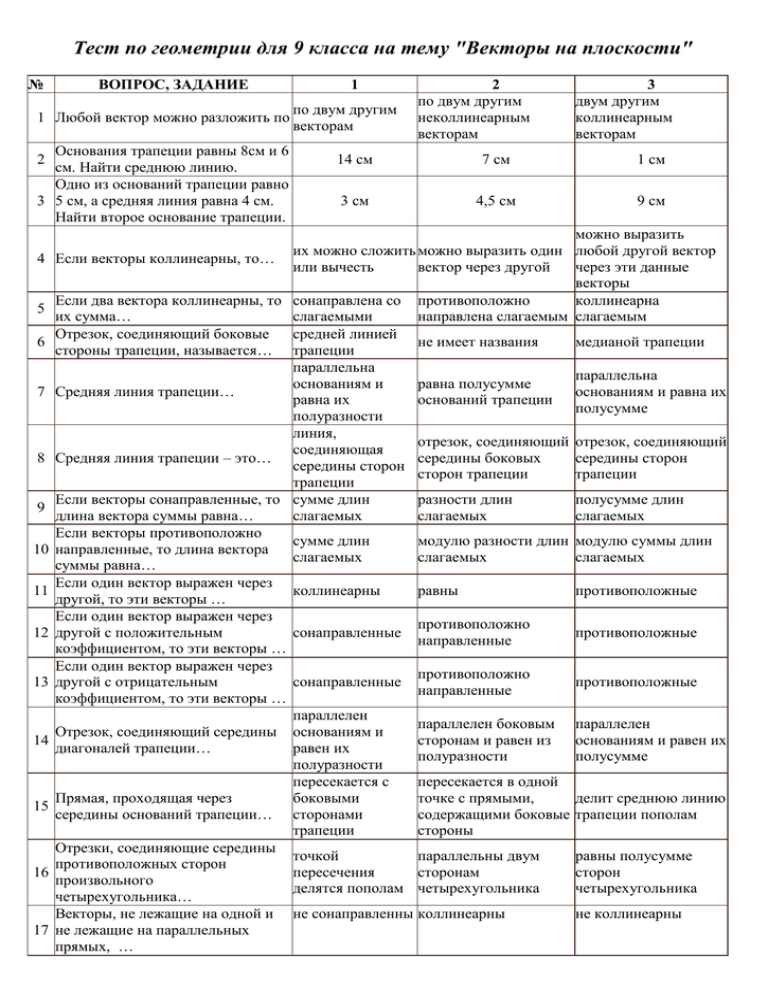
Тест по геометрии для 9 класса на тему "Векторы на плоскости"
№
ВОПРОС, ЗАДАНИЕ
1 Любой вектор можно разложить по
Основания трапеции равны 8см и 6
см. Найти среднюю линию.
Одно из оснований трапеции равно
3 5 см, а средняя линия равна 4 см.
Найти второе основание трапеции.
2
4
5
6
7
8
9
10
11
12
13
14
15
16
17
1
по двум другим
векторам
2
по двум другим
неколлинеарным
векторам
3
двум другим
коллинеарным
векторам
14 см
7 см
1 см
3 см
4,5 см
9 см
можно выразить
их можно сложить можно выразить один любой другой вектор
Если векторы коллинеарны, то…
или вычесть
вектор через другой
через эти данные
векторы
Если два вектора коллинеарны, то сонаправлена со противоположно
коллинеарна
их сумма…
слагаемыми
направлена слагаемым слагаемым
Отрезок, соединяющий боковые
средней линией
не имеет названия
медианой трапеции
стороны трапеции, называется… трапеции
параллельна
параллельна
основаниям и
равна полусумме
Средняя линия трапеции…
основаниям и равна их
равна их
оснований трапеции
полусумме
полуразности
линия,
отрезок, соединяющий отрезок, соединяющий
соединяющая
Средняя линия трапеции – это…
середины боковых
середины сторон
середины сторон
сторон трапеции
трапеции
трапеции
Если векторы сонаправленные, то сумме длин
разности длин
полусумме длин
длина вектора суммы равна…
слагаемых
слагаемых
слагаемых
Если векторы противоположно
сумме длин
модулю разности длин модулю суммы длин
направленные, то длина вектора
слагаемых
слагаемых
слагаемых
суммы равна…
Если один вектор выражен через
коллинеарны
равны
противоположные
другой, то эти векторы …
Если один вектор выражен через
противоположно
другой с положительным
сонаправленные
противоположные
направленные
коэффициентом, то эти векторы …
Если один вектор выражен через
противоположно
другой с отрицательным
сонаправленные
противоположные
направленные
коэффициентом, то эти векторы …
параллелен
параллелен боковым параллелен
Отрезок, соединяющий середины основаниям и
сторонам и равен из
основаниям и равен их
диагоналей трапеции…
равен их
полуразности
полусумме
полуразности
пересекается с
пересекается в одной
Прямая, проходящая через
боковыми
точке с прямыми,
делит среднюю линию
середины оснований трапеции… сторонами
содержащими боковые трапеции пополам
трапеции
стороны
Отрезки, соединяющие середины
точкой
параллельны двум
равны полусумме
противоположных сторон
пересечения
сторонам
сторон
произвольного
делятся пополам четырехугольника
четырехугольника
четырехугольника…
не коллинеарны
Векторы, не лежащие на одной и не сонаправленны коллинеарны
не лежащие на параллельных
прямых, …
В треугольнике АВС векторы АВ и
коллинеарные
АС …
сонаправлены с
В равнобедренной трапеции
вектором,
19 векторы, содержащие основания
содержащим
среднюю линию.
18
Если два вектора не лежат на
20 параллельных прямых и не лежат
на одной прямой, то…
Критерии оценивания:
«5» - 18-20 верных ответов;
«4» - 15-17 верных ответов;
«3» - 11-14 верных ответов;
«2» - 0-10 баллов.
Время выполнения – 8-10 минут.
они равны
не коллинеарные
сонаправленные
коллинеарны вектору,
параллельны средней
содержащему среднюю
линии
линию
любой другой
один из этих векторов
ненулевой вектор
можно выразить через
можно выразить через
другой
эти векторы