Нахождение числа по его дроби

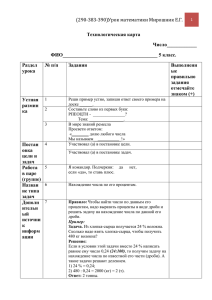
Урок математики в 6 классе по теме
«Нахождение числа по его дроби».
Цели урока: образовательная - ввести правило нахождения числа по его дроби и показать
его применение при решении задач; повторить правила нахождения дроби от числа,
умножения дробей, деления дробей, перевода процентов в десятичную дробь;
воспитательная - воспитывать уважение к мнению товарища и умение его выслушать;
развивающая - развивать математическую речь учащихся.
Тип урока: «открытие» нового знания (изучение и первичное закрепление новых
знаний).
Ход урока.
1. Актуализация опорных знаний.
У. – Здравствуйте, ребята, садитесь. Начинаем урок математики. В начале урока повторим
деление дробей и перевод процентов в десятичную дробь.
2
3
5
3
На доске примеры: 8 : ;300 : ;20 : ;1,5 :
.
5
8
8
16
Представить проценты в виде десятичных дробей: 7 %, 18 %, 55 %.
2. «Открытие» темы урока.
У. – Послушайте задачу: площадь катка 200 м2, расчистили от снега 2/5 катка. Сколько
квадратных метров расчистили?
2
Д. – 200  = 80 (м2).
5
У. – Как называются такие задачи? По какому правилу они решаются?
Д. – Такие задачи называются задачами на нахождение дроби от числа и решаются по
правилу: чтобы найти дробь от числа, нужно число умножить на дробь.
У. – Хорошо. Попробуйте сформулировать название обратной задачи.
Д. – Нахождение числа по его дроби.
У. – Такой и будет тема нашего сегодняшнего урока. Запишите.
Какова цель урока?
Д. – Научиться решать задачи на нахождение числа по его дроби.
3. Закрепление нового материала.
У. – Сейчас Серёжа выступит в роли учителя и расскажет, как решаются такие задачи.
(Серёжа выходит к доске и объясняет решение задачи 1 из учебника)
У. – Спасибо, Серёжа, садись.
У. - Следующие два вида задач на нахождение числа по его дроби вы разберёте по учебнику,
работая в группах. 1 группа (Наташа, Кристина, Настя и Олег) разберёте задачу 2. 2 группа
(Серёжа, Андрей и Лёша) разберёте задачу 3. Затем лидеры групп запишут и объяснят
задачу на доске, остальные – запишут в тетрадях.
(Дети работают в группах, затем лидеры – у доски)
У. – Что общего в решениях этих задач?
Д. – Они решаются с помощью деления.
У. – Попробуйте сформулировать правило нахождения числа по его дроби.
Д. – Чтобы найти число по его дроби, нужно число разделить на дробь.
У. – Сравните его с правилом в учебнике и запишите в тетрадь.
(Дети читают правило по учебнику и записывают его в тетрадь)
У. – А теперь поработайте в парах: Наташа и Кристина - № 650, Олег и Настя - № 647,
Серёжа и Андрюша - № 653, Лёша и я - № 654.
(Дети решают задачи из учебника)
4. Рефлексия деятельности.
У. – Сравните свои решения с эталоном, посмотрите, у кого какие ошибки допущены,
исправьте их и постарайтесь не допускать ошибок в самостоятельной работе.
(Дети выполняют самостоятельную работу на листочках и сдают учителю)
5. Итог урока и домашнее задание.
У. – Поведём итог урока. Какую цель ставили на уроке?
Д. – Научиться решать задачи на нахождение числа по его дроби.
У. – Кто может с полным правом сказать, что «я научился решать такие задачи»? Кому
показались трудными такие задачи? Сформулируйте правило решения задач на нахождение
числа по его дроби.
У. – Домашнее задание: № 680, 681, 691 (а), сильным уч-ся по желанию № 682.
Условное обозначение: У. – учитель, Д. - дети
Самостоятельная работа.
1 вариант.
1. Девочка потеряла 30 бусинок, что составляло 5/6 всей нити бус. Сколько бусинок было на
нитке?
2. Дочери 12 лет. Её возраст составляет 40 % возраста матери. Сколько лет матери?
3. Определить длину отрезка, если 0,6 его длины равна 15 см.
2 вариант.
1. Сыну 10 лет. Его возраст составляет 2/7 возраста отца. Сколько лет отцу?
2. Какова сумма денег, если 12 р. составляют 0,75 имеющейся суммы?
3. Турист проплыл на байдарке 504 км, что составило 36 % всего пути. Найти длину всего
пути.