№ Наименов. Тема К-во Тип

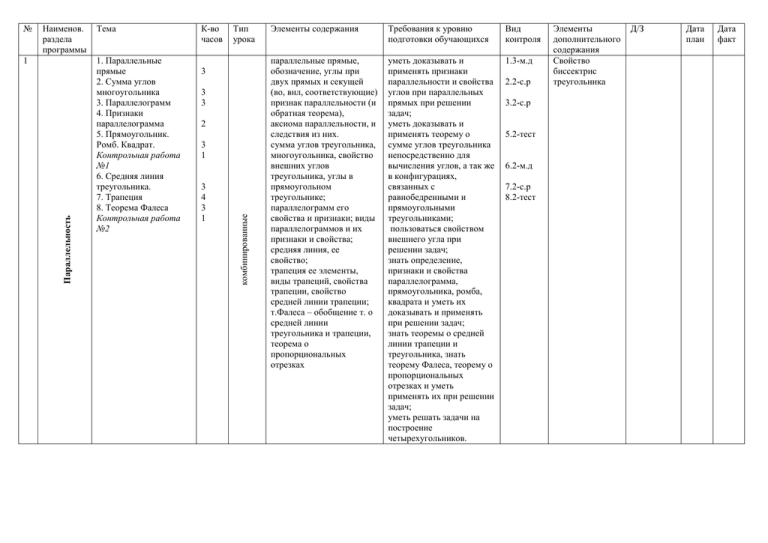
Наименов.
раздела
программы
Параллельность
1
Тема
1. Параллельные
прямые
2. Сумма углов
многоугольника
3. Параллелограмм
4. Признаки
параллелограмма
5. Прямоугольник.
Ромб. Квадрат.
Контрольная работа
№1
6. Средняя линия
треугольника.
7. Трапеция
8. Теорема Фалеса
Контрольная работа
№2
К-во
часов
Тип
урока
3
3
3
2
3
1
3
4
3
1
комбинированные
№
Элементы содержания
Требования к уровню
подготовки обучающихся
Вид
контроля
параллельные прямые,
обозначение, углы при
двух прямых и секущей
(во, внл, соответствующие)
признак параллельности (и
обратная теорема),
аксиома параллельности, и
следствия из них.
сумма углов треугольника,
многоугольника, свойство
внешних углов
треугольника, углы в
прямоугольном
треугольнике;
параллелограмм его
свойства и признаки; виды
параллелограммов и их
признаки и свойства;
средняя линия, ее
свойство;
трапеция ее элементы,
виды трапеций, свойства
трапеции, свойство
средней линии трапеции;
т.Фалеса – обобщение т. о
средней линии
треугольника и трапеции,
теорема о
пропорциональных
отрезках
уметь доказывать и
применять признаки
параллельности и свойства
углов при параллельных
прямых при решении
задач;
уметь доказывать и
применять теорему о
сумме углов треугольника
непосредственно для
вычисления углов, а так же
в конфигурациях,
связанных с
равнобедренными и
прямоугольными
треугольниками;
пользоваться свойством
внешнего угла при
решении задач;
знать определение,
признаки и свойства
параллелограмма,
прямоугольника, ромба,
квадрата и уметь их
доказывать и применять
при решении задач;
знать теоремы о средней
линии трапеции и
треугольника, знать
теорему Фалеса, теорему о
пропорциональных
отрезках и уметь
применять их при решении
задач;
уметь решать задачи на
построение
четырехугольников.
1.3-м.д
2.2-с.р
3.2-с.р
5.2-тест
6.2-м.д
7.2-с.р
8.2-тест
Элементы
дополнительного
содержания
Свойство
биссектрис
треугольника
Д/З
Дата
план
Дата
факт
Движение
3.
13. Центральная
симметрия
14. Поворот. симметрия
n-го порядка
15. Осевая симметрия
16. Параллельный
перенос
17. Движение.
Равенство фигур.
Контрольная работа
№4.
2
3
3
4
1
комбинированные
9. Углы, связанные с
окружностью
10. Многоугольники,
вписанные в
окружность.
11. Многоугольники,
описанные около
окружности.
12. Замечательные
точки в треугольнике.
Контрольная работа
№3
1
1
1
1
1
1
комбинированные
Многоугольники и окружность
2.
Центральный угол,
вписанный угол, дуга,
свойства вписанных углов,
измерение дуг и свойства
дуг;
вписанные
многоугольники и их
свойства; центр
окружности, описанной
около многоугольника;
многоугольник, описанный
около окружности, центр
окружности, вписанной в
многоугольник;
точка пересечения
биссектрис; точка
пересечения серединных
перпендикуляров, точка
пересечения высот
(ортоцентр), точка
пересечения медиан
(центроид), отношение
медиан.
центральная симметрия,
центрально-симметричные
фигуры, свойства
центральной симметрии
поворот, симметрия n-го
порядка, ее центр, свойства
поворота;
осевая симметрия, ось
симметрии, фигуры,
симметричные
относительно оси,
свойства осевой
симметрии
вектор, направление, длина
вектора, равенство
векторов, ноль-вектор,
параллельный перенос,
свойства параллельного
переноса;
движение; примеры
движений, композиция
движений, свойства
движений, равенство
фигур как движение
- знать и уметь доказывать
факты о центрах
вписанных и описанных
окружностей;
- знать свойства углов,
вписанных в окружность и
уметь применять их при
решении задач;
знать свойства
замечательных точек
треугольника и уметь
применять их при решении
задач.
9.2 м.д
10.2 с.р
11.3 с.р
12.2 с.р
уметь строить точки,
отрезки, простейшие
изученные фигуры,
симметричные
относительно точки или
прямой; а также
полученные в результате
поворота и параллельного
переноса, уметь различать
центрально-симметричные
фигуры и фигуры
симметричные
относительно оси, уметь
находить центр и ось
симметрии фигуры;
знать понятие вектора;
направленности векторов;
направление, модуль
вектора, свойства
векторов;
знать связь движение –
равенство фигур; свойства
движения.
13.2-м.д
14.2с.р
15.2-м.д
16.2-с.р
17.2-тест
п.44 Паркеты
Элементы тригонометрии
5.
22.
Тригонометрические
функции острого угла.
23.
Тригонометрические
тождества
24.
Тригонометрические
функции тупого угла
25. Теорема косинусов.
26. Теорема синусов.
27. Длина окружности.
Контрольная работа №6
2
2
2
3
1
комбинированные
18. Подобие
треугольников. 1ый
признак подобия.
19. 2ой и 3ий признаки
подобия треугольников.
20. Подобие фигур.
Гомотетия.
21. Теорема Пифагора.
Контрольная работа
№5.
2
2
2
2
2
2
комбинированные
Подобие
4.
подобие, коэффициент
подобия, подобные
фигуры, 1,2,3 признаки
подобия треугольников;
гомотетия, коэффициент
гомотетии; свойства
подобия и гомотетии;
т.Пифагора, соизмеримые
и несоизмеримые отрезки,
пифагорейские тройки
чисел.
синус, косинус, тангенс и
котангенс острого угла,
связь тригоном.функций и
сторон прямоугольного
треугольника, значение
триг. функций углов 30,
45,60 градусов
тригонометрич. тождества;
основные триг. тождества;
выражение синуса через
косинус и наоборот,
тригоном. функции углов
90, и от 90 до 180 градусов
теорема косинусов –
обобщение теоремы
Пифагора.
теорема синусов,
выражение сторон
треугольника через изв.
стороны и углы.
периметр правильного
многоугольника;
отношение периметров,
радиусов оп. и вп.
окружностей; формула
длины окружности, число
π , радианная мера угла,
радиан.
умение доказать подобие
треугольников с опорой на
признаки и вычислять
элементы подобных
треугольников в типичных
конфигурациях;
уметь применять теорему
Пифагора при решении
задач;
в задачах уметь вычленять
прямоугольные
треугольники и находить
неизвестные элементы;
уметь строить
гомотетичные фигуры с
заданным коэффициентом
гомотетии.
знать определения
тригоном. функций для
острых и тупых углов,
уметь находить
неизвестные элементы
прямоугольного
треугольника зная
определения триг.
функций;
- знать основные триг.
тождества, уметь ими
пользоваться при решении
задач
уметь доказывать и
применять теоремы
синусов и косинусов при
решении треугольников,
знать формулу длины
окружности, уметь
вычислять длину
окружности и длину дуги
при решении задач.
18.2м.д
19.2с.р
20.2м.д
21.2 тест
п.48 Золотое
сечение
22.2 м.д
23.2 мд
24.2 мд
25.2 с.р
26.2 с.р
27.2 м.д
п.56
Циклоидальные
кривые
Пояснительная записка
Календарно-тематическое планирование составлено на основе учебника по геометрии [2] в соответствии с программой для общеобразовательных
школ, гимназий, лицеев [1, c.23-27].
Основной задачей изучения курса геометрии 8 класса является формирование умений решать типичные задачи на вычисление, доказательство и
построение, опираясь на изученные в курсе теоретические сведения. При их решении учащиеся должны изображать на рисунках геометрические
фигуры, указанные в условиях, и выделять указанные фигуры на чертежах и моделях. При решении задач на вычисление значений геометрических
величин учащиеся должны уметь применять аппарат алгебры.
Нормативная продолжительность изучения этого содержания определена в соответствии с федеральным базисным планом основного общего
образования.
Планирование рассчитано на 2 часа в неделю, всего 68 часов.
Литература, используемая при составлении планирования
1. Программы для общеобразоват. школ, гимназий, лицеев: Математика. 5 – 11 кл. / Сост. Г.М. Кунецова, Н.Г. Миндюк. – 4-е изд., стереотип. – М.: Дрофа, 2004. – 320 с.
2. Геометрия 7 – 9 кл.; Учебник для общеобразовательных учреждений/ И.М. Смирнова, В.А. Смирнов. – М.: Мнемозина, 2007.
3. Дидактические материалы. Геометрия. 7, 8, 9 кл./И.М. Смирнова, В.А. Смирнов. – М. Мнемозина. 2005.
4. Методические рекомендации для учителя. Геометрия. 7, 8, 9 кл. ./И.М. Смирнова, В.А. Смирнов. – М. Мнемозина. 2005.