9 класс. основного общего образования в форме государственного выпускного экзамена.

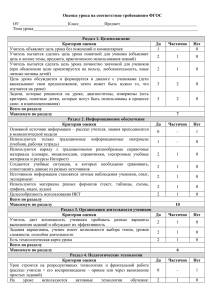
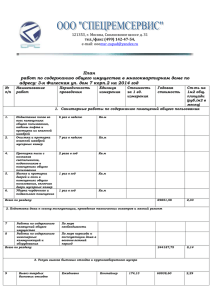
9 класс.
Государственная итоговая аттестация по образовательным программам
основного общего образования в форме государственного выпускного
экзамена.
Математика (устный экзамен) 2015-2016 учебный год.
Особенности экзаменационной работы ГВЭ-9 по математике (устная
форма)
Для проведения ГВЭ-9 по математике в устной форме разработаны
варианты билетов, включающие в себя задания как по курсу алгебры, так и по
курсу геометрии.
Билеты включают 5 заданий: теоретическая часть – два задания по
геометрии, практическая часть – одно задание по арифметике и два задания по
алгебре. Задания являются стандартными для курса математики основной
школы. Все они предполагают устное изложение решения, демонстрирующего
умение выпускника математически грамотно излагать ход решения, приводя
при этом необходимые пояснения и обоснования.
Задания в практической части экзаменационных билетах расположены по
нарастанию сложности. Задания 3 и 4 соответствуют уровню базовой
математической подготовки, среди них одно задание по арифметике и одно
задание по алгебре. Задание 5 (по курсу алгебры) соответствуют уровню
повышенной подготовки.
В первом вопросе экзаменационного билета от экзаменуемого требуется
воспроизвести определение геометрической фигуры или конфигурации,
формулировку теоремы, связанной с ее свойствами или признаками
(доказывать теорему не требуется), привести необходимые иллюстрирующие
примеры. Умение доказывать изученные в курсе свойства или признаки
геометрических фигур, сформулированные в виде теорем, экзаменуемый
должен продемонстрировать при ответе на второй вопрос билета.
БИЛЕТ №1
1. Параллельные прямые; свойство углов, образованных при пересечении
параллельных прямых секущей.
2. Признаки параллельности прямых (доказательство одного из признаков).
3. Задание, по разделу «Числа и вычисления» (проценты)
4. Задание, по разделу «Функции»
5. Задание, по разделу «Уравнения и неравенства»
БИЛЕТ №2
1. Равнобедренный треугольник; свойство углов при основании
равнобедренного треугольника.
2. Свойства медианы, биссектрисы, высоты равнобедренного треугольника,
проведённых к основанию (доказательство одного из свойств).
3. Задание, по разделу «Числа и вычисления» (решение текстовых задач)
4. Задание, по разделу «Функции»
5. Задание, по разделу «Уравнения и неравенства»
БИЛЕТ №3
1. Высота, биссектриса и медиана треугольника; свойства медианы,
биссектрисы, высоты равнобедренного треугольника, проведенных к
основанию.
2. Теорема о сумме углов треугольника (формулировка и доказательство).
3. Задание, по разделу «Числа и вычисления» (проценты)
4. Задание, по разделу «Функции»
5. Задание, по разделу «Уравнения и неравенства»
БИЛЕТ №4
1.
2.
3.
4.
5.
Признаки равенства треугольников.
Теорема о средней линии трапеции (формулировка и доказательство).
Задание, по разделу «Числа и вычисления» (решение текстовых задач)
Задание, по разделу «Функции»
Задание, по разделу «Уравнения и неравенства»
БИЛЕТ №5
1.
2.
3.
4.
5.
Параллелограмм; свойства и признак параллелограмма.
Теорема Пифагора (формулировка и доказательство)
Задание, по разделу «Числа и вычисления» (проценты)
Задание, по разделу «Функции»
Задание, по разделу «Уравнения и неравенства»
БИЛЕТ №6
1.
2.
3.
4.
5.
Прямоугольник, квадрат, ромб; их свойства.
Признаки параллельности прямых (доказательство одного из признаков).
Задание, по разделу «Числа и вычисления» (решение текстовых задач)
Задание, по разделу «Функции»
Задание, по разделу «Уравнения и неравенства»
БИЛЕТ №7
1. Трапеция; равнобедренная (равнобокая) трапеция; средняя линия
трапеции и ее свойства.
2. Свойства медианы, биссектрисы, высоты равнобедренного треугольника,
проведённых к основанию (доказательство одного из свойств).
3. Задание, по разделу «Числа и вычисления» (проценты)
4. Задание, по разделу «Функции»
5. Задание, по разделу «Уравнения и неравенства»
БИЛЕТ №8
1. Прямоугольный треугольник, свойство прямоугольного треугольника,
один из углов которого равен 30.
2. Теорема о сумме углов треугольника (формулировка и доказательство).
3. Задание, по разделу «Числа и вычисления» (решение текстовых задач)
4. Задание, по разделу «Функции»
5. Задание, по разделу «Уравнения и неравенства»
БИЛЕТ №9
1.
2.
3.
4.
5.
Теорема синусов: пример ее применения для решения треугольников.
Теорема о средней линии трапеции (формулировка и доказательство).
Задание, по разделу «Числа и вычисления» (проценты)
Задание, по разделу «Функции»
Задание, по разделу «Уравнения и неравенства»
БИЛЕТ №10
1.
2.
3.
4.
5.
Теорема косинусов: пример ее применения для решения треугольников.
Теорема Пифагора (формулировка и доказательство)
Задание, по разделу «Числа и вычисления» (решение текстовых задач)
Задание, по разделу «Функции»
Задание, по разделу «Уравнения и неравенства»
БИЛЕТ №11
1.
2.
3.
4.
5.
Теоремы о вписанной и описанной окружностях треугольника.
Признаки параллельности прямых (доказательство одного из признаков).
Задание, по разделу «Числа и вычисления» (проценты)
Задание, по разделу «Функции»
Задание, по разделу «Уравнения и неравенства»
БИЛЕТ №12
1. Косинус острого угла прямоугольного треугольника; пример его
применения при решении прямоугольных треугольников.
2. Свойства медианы, биссектрисы, высоты равнобедренного треугольника,
проведённых к основанию (доказательство одного из свойств).
3. Задание, по разделу «Числа и вычисления» (решение текстовых задач)
4. Задание, по разделу «Функции»
5. Задание, по разделу «Уравнения и неравенства»
БИЛЕТ №13
1. Синус острого угла прямоугольного треугольника; пример его
применения при решении прямоугольных треугольников.
2. Теорема о сумме углов треугольника (формулировка и доказательство).
3. Задание, по разделу «Числа и вычисления» (проценты)
4. Задание, по разделу «Функции»
5. Задание, по разделу «Уравнения и неравенства»
БИЛЕТ №14
1.
2.
3.
4.
5.
Признаки подобия треугольников.
Теорема о средней линии трапеции (формулировка и доказательство).
Задание, по разделу «Числа и вычисления» (решение текстовых задач)
Задание, по разделу «Функции»
Задание, по разделу «Уравнения и неравенства»
БИЛЕТ №15
1. Окружность, градусная мера дуги окружности; центральный угол,
вписанный угол; теорема о вписанном угле.
2. Теорема Пифагора (формулировка и доказательство)
3. Задание, по разделу «Числа и вычисления» (проценты)
4. Задание, по разделу «Функции»
5. Задание, по разделу «Уравнения и неравенства»