upload/images/files/практ_раб_№19,20(4)x

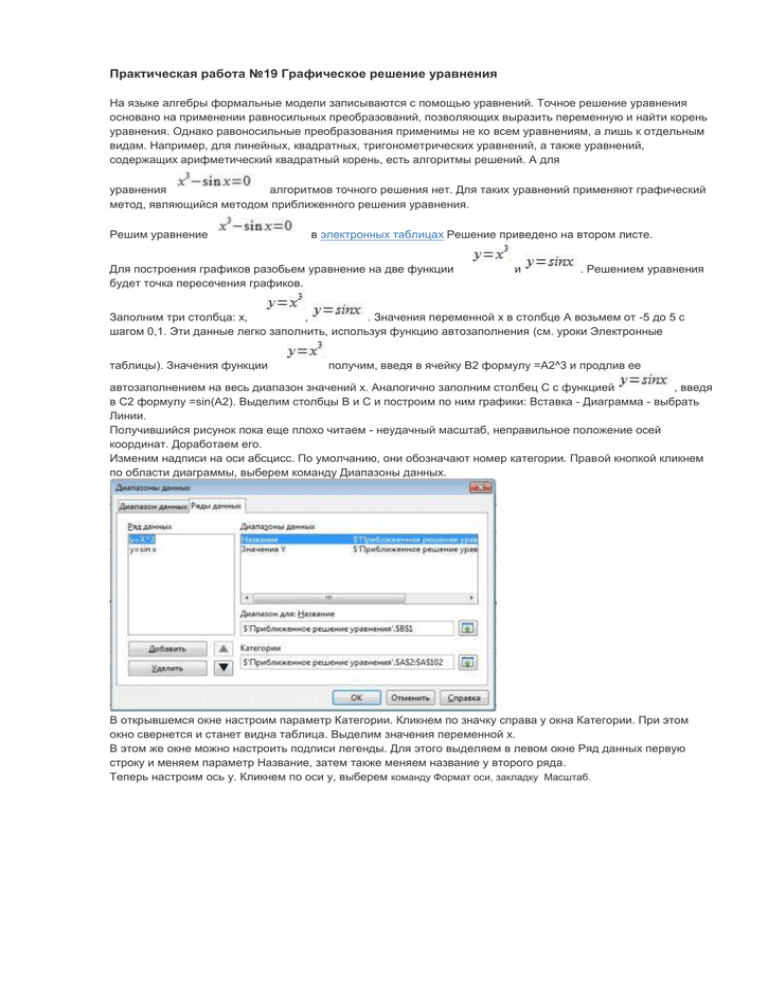
Практическая работа №19 Графическое решение уравнения
На языке алгебры формальные модели записываются с помощью уравнений. Точное решение уравнения
основано на применении равносильных преобразований, позволяющих выразить переменную и найти корень
уравнения. Однако равоносильные преобразования применимы не ко всем уравнениям, а лишь к отдельным
видам. Например, для линейных, квадратных, тригонометрических уравнений, а также уравнений,
содержащих арифметический квадратный корень, есть алгоритмы решений. А для
уравнения
алгоритмов точного решения нет. Для таких уравнений применяют графический
метод, являющийся методом приближенного решения уравнения.
Решим уравнение
в электронных таблицах Решение приведено на втором листе.
Для построения графиков разобьем уравнение на две функции
будет точка пересечения графиков.
и
. Решением уравнения
Заполним три столбца: х,
,
. Значения переменной х в столбце А возьмем от -5 до 5 с
шагом 0,1. Эти данные легко заполнить, используя функцию автозаполнения (см. уроки Электронные
таблицы). Значения функции
получим, введя в ячейку В2 формулу =А2^3 и продлив ее
автозаполнением на весь диапазон значений х. Аналогично заполним столбец С с функцией
, введя
в С2 формулу =sin(A2). Выделим столбцы В и С и построим по ним графики: Вставка - Диаграмма - выбрать
Линии.
Получившийся рисунок пока еще плохо читаем - неудачный масштаб, неправильное положение осей
координат. Доработаем его.
Изменим надписи на оси абсцисс. По умолчанию, они обозначают номер категории. Правой кнопкой кликнем
по области диаграммы, выберем команду Диапазоны данных.
В открывшемся окне настроим параметр Категории. Кликнем по значку справа у окна Категории. При этом
окно свернется и станет видна таблица. Выделим значения переменной х.
В этом же окне можно настроить подписи легенды. Для этого выделяем в левом окне Ряд данных первую
строку и меняем параметр Название, затем также меняем название у второго ряда.
Теперь настроим ось у. Кликнем по оси у, выберем команду Формат оси, закладку Масштаб.
Снимаем галочки Автоматически и указываем наименьшее значение -5, наибольшее 5.
Теперь перейдем к закладке Расположение. Здесь настроим нужное нам пересечение осей.
Вот теперь получился хорошо читаемый рисунок.
По нему видно, что уравнение
имеет три корня: 0 и два симметричных значения положительное и отрицательное. Точного решения мы не получили, но уже можем ответить на ряд вопросов
по уравнению и оценить примерное значение корней.
Из приведенного примера видно, что графический метод дает только приближенные значения корней и может
применяться при ответе на вопросы:
Есть ли корни у данного уравнения и если есть, то сколько?
Какие по знаку корни уравнения?
В какой промежуток входят корни уравнения?
Практическое задание
Докажите с помощью моделирования, что уравнение
а=0, не имеет корней при а<0.
имеет два корня при а>0, один корень при