2.2 Тематич

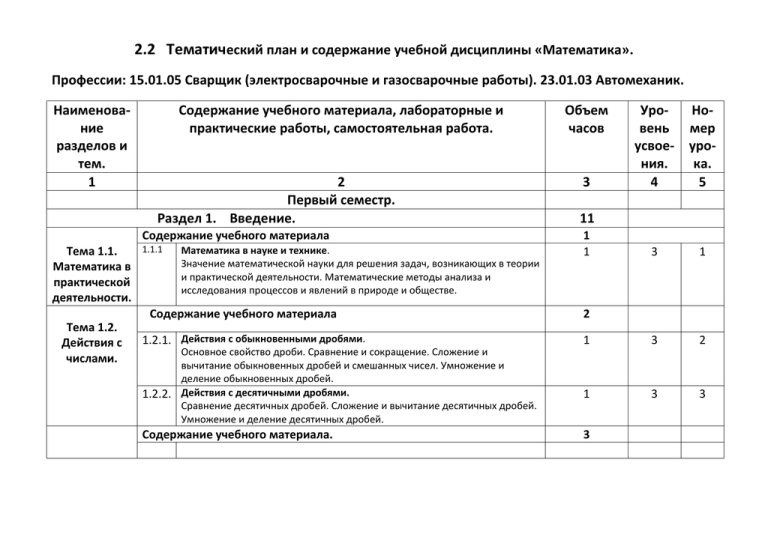
2.2 Тематический план и содержание учебной дисциплины «Математика».
Профессии: 15.01.05 Сварщик (электросварочные и газосварочные работы). 23.01.03 Автомеханик.
Наименование
разделов и
тем.
1
Содержание учебного материала, лабораторные и
практические работы, самостоятельная работа.
2
Первый семестр.
Раздел 1. Введение.
Содержание учебного материала
Тема 1.1.
Математика в
практической
деятельности.
1.1.1
Математика в науке и технике.
Значение математической науки для решения задач, возникающих в теории
и практической деятельности. Математические методы анализа и
исследования процессов и явлений в природе и обществе.
Содержание учебного материала
Тема 1.2.
Действия с
числами.
1.2.1. Действия с обыкновенными дробями.
Основное свойство дроби. Сравнение и сокращение. Сложение и
вычитание обыкновенных дробей и смешанных чисел. Умножение и
деление обыкновенных дробей.
1.2.2. Действия с десятичными дробями.
Сравнение десятичных дробей. Сложение и вычитание десятичных дробей.
Умножение и деление десятичных дробей.
Содержание учебного материала.
Объем
часов
Уровень
усвоения.
4
Номер
урока.
5
3
1
1
3
2
1
3
3
3
11
1
1
2
3
Тема 1.3.
Решение
уравнений.
Тема 1.4.
Неравенства.
1.3.1. Линейные уравнения.
Определение линейного уравнения с одной переменной. Корни уравнения.
Равносильность уравнений. Область допустимых значений уравнения.
Решение линейных уравнений с одной переменной.
1.3.2. Квадратные уравнения.
Общий вид квадратного уравнения. Вычисление дискриминанта.
Двукратный корень. Два действительных корня. Отсутствие действительных
корней. Биквадратное уравнение.
1.3.3. Системы уравнений.
Общий вид системы уравнений с двумя переменными. Решение системы
уравнений. Метод алгебраического сложения. Метод подстановки.
Содержание учебного материала.
1.4.1.
1.4.2.
1.4.3.
Тема 1.5.
Линейные неравенства.
Определение неравенства. Их равносильность. Строгие, нестрогие
неравенства. Истинные и ложные неравенства. Основные свойства
неравенств.
Системы неравенств.
Определение системы неравенств. Двойные неравенства. Решение
неравенства. Нахождение области допустимых значений.
Квадратные неравенства.
Графический метод решения квадратных неравенств. Метод интервалов
(промежутков).
Содержание учебного материала.
1
3
4
1
3
5
1
3
6
1
3
7
1
3
8
1
3
9
3
2
Решение
текстовых
задач.
1.5.1.
Текстовые задачи на работу.
Производительность труда и время, необходимое для выполнения работы,
– взаимно обратные величины.
Общий порядок решения задач с помощью уравнений:
1) введение переменной,
2) составление уравнения,
3) решение уравнения,
4) анализ решения.
1.5.2 Текстовые задачи на движение.
Физический смысл задачи. Путь. Скорость. Время. Единицы измерения.
Средняя скорость. Движение по реке: собственная скорость, скорость в
стоячей воде, скорость течения реки.
Внеаудиторная самостоятельная работа:
1.«Математика в быту» - сообщение.
2. «Математика в моей профессии» - презентация.
3. «Действия с обыкновенными дробями» - проработка конспекта.
4. «Действия с десятичными дробями» - работа с папкой «Учись учиться».
5. «Уравнения. Неравенства» - дифференцированная домашняя работа.
Раздел 2. Алгебра.
Содержание учебного материала.
2.1.1.
Тема 2.1.
Развитие
понятия о
числе.
2.1.2.
2.1.3.
Целые и рациональные числа.
Натуральные числа. Действия над натуральными числами.
Свойства сложения и умножения. Простые и составные числа.
Целые числа и обыкновенные дроби.
Иррациональные числа.
Бесконечные непериодические десятичные дроби. Примеры
иррациональных чисел.
Действительные числа.
Объединение множества рациональных чисел и множества
иррациональных чисел. Обозначения. Действия сложения и
1
3
10
1
3
11
13
1
3
12
1
3
13
1
3
14
6
124
2.1.4.
2.1.5.
2.1.6.
2.1.7.
2.1.8
2.1.9.
умножения действительных чисел.
Наибольший общий делитель.
Определение наибольшего общего делителя. Алгоритм
нахождения наибольшего общего делителя нескольких
натуральных чисел: разложение на множители, составление
произведения всех простых множителей, общих для данных
чисел.
Наименьшее общее кратное.
Определение наименьшего общего кратного. Алгоритм
нахождения наименьшего общего кратного: разложение на
множители, выписывание всех множителей какого-нибудь
одного из чисел, дополнение недостающих множителей из
других чисел и вычисление их произведения.
Проценты.
Что такое процент. Связь процента с десятичными дробями.
Правило обращения десятичной дроби в проценты.
Основные задачи на проценты.
Нахождение процентов от данного числа. Нахождение числа по
числу процентов.
Модуль числа.
Определение модуля. Геометрическая интерпретация модуля.
Уравнения с модулем.
Приближенные вычисления.
Приближенные значения вычислений. Правило округления
чисел. Примеры. Действия над приближенными значениями
чисел.
1
3
15
1
3
16
1
3
17
1
3
18
1
3
19
1
3
20
2.1.10.
Погрешности вычислений.
Абсолютная погрешность приближенного значения числа.
Граница абсолютной погрешности. Нахождение абсолютной
погрешности измерения детали. Относительная погрешность
приближенного значения числа.
1
3
21
2.1.11.
Комплексные числа.
Определение комплексного числа. Геометрическое
изображение комплексного числа. Алгебраическая форма
комплексного числа. Модуль комплексного числа. Сопряженные
комплексные числа. Мнимая единица.
1
3
22
2.1.12.
Решение задач.
Арифметические действия с числами, простыми и смешанными
дробями. Нахождение приближенных значений величин.
Основные задачи на проценты.
Контрольная работа №1.
Готовность выполнять арифметические действия с числами,
дробями, находить приближенные значения величин,
наибольший общий делитель, наименьшее общее кратное,
решать задачи с процентами.
1
3
23
1
3
24
2.1.13.
Внеаудиторная самостоятельная работа:
1. Развитие понятия числа – составление схемы.
2. «Обращение обыкновенной дроби в бесконечную десятичную
периодическую дробь» - изучение материала в папке «Учись учиться».
3. «Приближенные вычисления» - составление конспекта.
4. «Комплексные числа» - проработка конспекта.
5. « Применение процентов в экономических расчетах» - доклад.
6. « Наибольший общий делитель» - дифференцированное домашнее задание.
7. «Наименьшее общее кратное» - дифференцированное домашнее задание.
9
Содержание учебного материала.
2.2.1.
2.2.2.
Тема 2.2.
Корни,
степени,
логарифмы.
2.2.3.
2.2.4.
2.2.5.
2.2.6.
2.2.7.
2.2.8.
Корень натуральной степени.
Определение арифметического корня. Свойства арифметических
корней. Корень нечетной степени из отрицательного числа.
Степень с рациональным показателем.
Степень с дробными показателями. Свойства степени с дробными
показателями.
Свойства корней с рациональными показателями.
Корень из произведения двух неотрицательных чисел. Корень из
частного двух чисел. Внесение множителя под знак корня.
Вынесение множителя из-под знака корня.
Степень с действительным показателем.
Степень с нулевым показателем. Степень с натуральным
показателем. Степень с отрицательным целым показателем.
Степень с дробным показателем. Свойства степени.
Свойства степеней с рациональным показателем.
Возведение в натуральную степень. Возведение в нулевую
степень и целую отрицательную степень. Возведение в дробную
степень.
Решение задач.
Решение задач с применением свойств степеней с
рациональным показателем и свойств корней с рациональным
показателем.
Понятие логарифма.
Рассмотреть задачу с неизвестным основанием степени.
Рассмотреть задачу с неизвестным показателем степени. Ввести
понятие логарифма и отработать на примерах. Существование
логарифма только для положительных чисел.
Основное логарифмическое тождество.
Определение логарифма. Основное логарифмическое тождество.
Логарифмирование.
28
1
3
25
1
3
26
1
3
27
1
3
28
1
3
29
1
3
30
1
3
31
1
3
32
2.2.9.
2.2.10.
2.2.11.
2.2.12.
2.2.13.
2.2.14
2.2.15
2.2.16.
2.2.17.
Свойства логарифмов.
Логарифм произведения, частного и степени. Логарифм единицы,
логарифм основания. Ограничение существования логарифмов.
Решение задач.
Задачи на определение логарифма. Задачи на основное
логарифмическое тождество и на свойства логарифмов.
Десятичный и натуральный логарифм.
Логарифм по основанию 10. Логарифм по основанию е.
существование десятичного и натурального логарифмов и их
свойства.
Переход к новому основанию.
Формула перехода к логарифму с новым основанием. Отработка
этой формулы в задачах.
Действия с логарифмами.
Сложение, вычитание логарифмов. Возведение в степень.
Логарифмирование и потенцирование.
Решение задач.
Задачи с десятичным логарифмом. Задачи на применения
формулы перехода к новому основанию.
Алгебраические выражения и их преобразование.
Виды алгебраических выражений. Область определения
алгебраического выражения. Тождественные преобразования
выражения.
Рациональные выражения и их преобразование.
Сложение, вычитание, умножение, деление рациональных
дробей.
Возведение дроби в натуральную степень. Использование формул
сокращенного умножения.
Решение задач.
Задачи на преобразование алгебраических выражений. Задачи на
преобразование рациональных выражений.
1
3
33
1
3
34
1
3
35
1
3
36
1
3
37
1
3
38
1
3
39
1
3
40
1
3
41
2.2.18.
2.2.19.
2.2.20.
2.2.21.
2.2.22.
2.2.23.
2.2.24.
2.2.25.
2.2.26.
Иррациональные выражения и их преобразование.
Понятие иррационального выражения. Использование свойств
радикалов и степени с рациональным показателем.
Степенные выражения и их преобразование.
Степень с натуральным показателем. Степень с рациональным
показателем для неотрицательного числа. Степень с целым
показателем. Степень с действительным показателем.
Применение свойств степеней в преобразовании степенных
выражений.
Решение задач. Задачи на преобразование иррациональных
выражений. Задачи на преобразование степенных выражений.
Показательные выражения и их преобразование. Область
определения показательного выражения. Множество значений.
Свойства степени в преобразовании показательных выражений.
Решение задач.
Задачи на преобразование показательных выражений.
Логарифмические выражения и их преобразование.
Понятие логарифмического выражения. Свойства логарифмов:
логарифм произведения, логарифм частного, логарифм степени в
преобразовании логарифмических выражений.
Логарифмирование и потенцирование.
Решение задач.
Решение задач на преобразование логарифмических выражений.
Использование свойств логарифма и формулы перехода в
преобразовании логарифмических выражений.
Преобразование комбинированных выражений.
Понятие трансцендентных выражений, содержащих переменные
под знаком комбинированной функции, т.е. под знаком
показательной, логарифмической функции и их преобразование.
1
3
42
1
3
43
1
3
44
1
3
45
1
3
46
1
3
47
1
3
48
1
3
49
Тождественные преобразования.
1
3
50
Понятие тождества, равенства верного при всех допустимых
значениях входящих в него переменных. Соответственные
значения выражений. Пропорция. Тождественные
преобразования выражения с учетом допустимых значений
переменных.
2.2.27.
Решение задач.
Решение задач на применение свойств корней с рациональным
показателем. Решение задач на применение свойств степени с
рациональным показателем. Задачи на применение свойств
логарифма. Задачи на преобразование степенных выражений.
2.2.28.
Контрольная работа №2.
Готовность находить значение корня, степени, логарифма,
выполнять преобразование выражений, применяя формулы,
связанные со свойствами корней, степеней, логарифмов,
проводить практические расчеты по формулам.
Внеаудиторная самостоятельная работа:
1 . « Л. Эйлер – ученый математик» - сообщение.
2. «Из истории логарифмов» - доклад.
3. «Степень с рациональным показателем» - изучение материала в папке «Учись
учиться».
4. « О происхождении терминов и обозначений» - сообщение.
5. «Корень натуральной степени» - составление опорного конспекта.
6. «Понятие логарифм. Свойства логарифма» - составление опорного конспекта.
7. «Десятичный и натуральный логарифмы» - сообщение.
8. «Логарифмические преобразования» - дифференцированная домашняя работа.
9. « Иррациональное число е» - сообщение.
10. «Логарифмы в экономике» - доклад.
Содержание учебного материала
2.3.1
Тема 2.3.
Радианная мера угла.
Измерение углов. Центральный угол. Радианная мера угла.
Соотношение между радианной и градусной мерой углов. Число π.
1
3
51
1
3
52
3
53
12
33
1
Основы
тригонометрии.
2.3.2.
2.3.3.
2.3.4.
2.3.5.
2.3.6.
2.3.7.
2.3.8.
Таблица соответствия градусной и радианной мер углов.
Поворот точки вокруг начала координат.
Единичная окружность. Точка тригонометрической окружности с
координатами (1;0). Положительный угол – движение точки против
часовой стрелки. Отрицательный угол – движение точки по часовой
стрелке.
Синус, косинус, тангенс и котангенс.
Тригонометрические окружности. Точка тригонометрической
окружности. Соотношения в прямоугольном треугольнике. Синус угла –
ордината точки. Косинус угла – абсцисса точки. Тангенс угла –
отношение синуса угла к его косинусу. Котангенс угла – отношение
косинуса угла к его синусу.
Свойства синуса, косинуса, тангенса и котангенса.
Определение синуса, косинуса, тангенса и котангенса. Знаки синуса,
косинуса, тангенса и котангенса. Четность и нечетность.
Основные тригонометрические тождества.
Зависимость между синусом, косинусом, тангенсом одного и того же
угла. Основное тригонометрическое тождество. Зависимость между
тангенсом и котангенсом.
Применение основных тригонометрических тождеств.
Понятие тождества. Допустимые значения переменных.
Доказательство тождественных выражений. Преобразование левой
части выражения к правой и наоборот. Нахождение разности между
левой и правой частями выражения.
Решение задач.
Вычисление значений тригонометрических функций. По значению
одной из тригонометрических функций найти значения остальных трех.
Доказательство тригонометрических тождеств.
Формулы приведения.
Таблицы значений синуса, косинуса, тангенса и котангенса для острых
углов первой четверти тригонометрической окружности. Формулы
1
3
54
1
3
55
1
3
56
1
3
57
1
3
58
1
3
59
1
3
60
2.3.9.
2.3.10
2.3.11.
2.3.12.
2.3.13.
приведения сводят значения остальных углов к значениям для острых
углов. Правило для запоминания формул приведения.
Применение формул приведения.
Таблица значений тригонометрических функций. Правило для
запоминания формул приведения.
Формулы сложения.
Таблица значений тригонометрических функций. Формулы сложения.
Применение формул сложения.
Таблица значений тригонометрических функций. Применение формул
сложения.
Решение задач.
Задачи на применение формул сложения и формул приведения.
Таблица значений тригонометрических функций.
Формулы двойного угла.
Формулы сложения.
Таблица значений тригонометрических функций.
Синус, косинус, тангенс двойного угла.
1
3
61
1
3
62
1
3
63
1
3
64
1
3
65
66
2.3.14.
Применение формул двойного угла.
Основные тригонометрические тождества. Таблица значений
тригонометрических функций. Синус, косинус, тангенс двойного угла и
их применение в задачах.
2.3.15.
Решение задач.
Задания на вычисление тригонометрических функций двойного угла.
Упрощение выражений.
1
3
1
3
67
2.3.16.
Контрольная работа №3.
Готовность находить значения тригонометрических функций по
заданному значению при различных способах задания функции,
применяя основные формулы тригонометрии, выполнять
преобразования выражений.
1
3
68
2.3.17.
Формулы половинного угла.
Формулы синуса, косинуса половинного угла. Формулы понижения
степени. Формула тангенса половинного угла.
1
3
69
2.3.18.
Решение задач.
Таблица значений тригонометрических функций. Задания на
применение формул половинного угла. Нахождение синуса и косинуса
угла через тангенс половинного угла.
1
3
70
2.3.19.
Формулы суммы и разности. Формулы сложения. Формулы двойного
угла. Сумма и разность синусов. Сумма и разность косинусов.
Применение формул суммы и разности.
Применение формул суммы и разности синусов и косинусов при
упрощении выражения. Задания на вычисление. Доказательство
тождеств.
Преобразование простейших тригонометрических выражений.
Основные формулы тригонометрии. Формулы двойного угла. Формулы
суммы и разности. Упрощение простейших тригонометрических
выражений.
Решение задач.
Вычисление значений тригонометрических выражений.
Преобразование простейших тригонометрических выражений.
Доказательство тождеств.
Арксинус и арккосинус.
Геометрическая интерпретация арксинуса и арккосинуса. Область
определения. Область значений. Монотонность. Основные значения
функций арксинуса и арккосинуса.
Арктангенс и арккотангенс.
Геометрическая интерпретация арктангенса и арккотангенса. Область
определения. Область значений. Монотонность. Основные значения
функции арктангенса и арккотангенса.
Простейшие тригонометрические уравнения.
Понятие простейших тригонометрических уравнений. Решение
простейших тригонометрических уравнений. Частные случаи.
Геометрическая интерпретация решений простейших
2
3
71
1
3
72
1
3
73
1
3
74
1
3
75
1
3
76
1
3
77
2.3.20.
2.3.21.
2.3.22.
2.3.23.
2.3.24.
2.3.25.
2.3.26.
2.3.27.
2.3.28.
2.3.29.
2.3.30.
2.3.31.
2.3.32.
2.3.33.
тригонометрических уравнений.
Решение уравнений вида 𝐬𝐢𝐧 𝒙 = 𝒂.
Формула решений данного уравнения. Частные случаи. Арксинус
отрицательных чисел.
Решение уравнений вида 𝐜𝐨𝐬 𝒙 = 𝒂.
Формула решений данного уравнения. Частные случаи. Арккосинус
отрицательных чисел.
Решение уравнений вида tgx=a и ctgx=a.
Формулы решений данных уравнений. Нахождение арктангенсов
отрицательных чисел через значения арктангенсов положительных
чисел.
Решение простейших тригонометрических уравнений.
Частные случаи. Нахождение арксинусов, арккосинусов, арктангенсов и
арккотангенсов отрицательных чисел через значения положительных
чисел.
Простейшие тригонометрические неравенства.
Косинус – абсцисса точки единичной окружности. Синус – ордината
точки единичной окружности. Примеры простейших
тригонометрических неравенств.
Решение простейших тригонометрических неравенств.
Примеры простейших тригонометрических неравенств. Решение
простейшего тригонометрического неравенства – нахождение
множества всех значений аргумента, которые обращают данное
неравенство в верное числовое равенство.
Решение задач.
Решение простейших тригонометрических уравнений. Частные случаи.
Решение простейших тригонометрических неравенств.
Контрольная работа №4.
Готовность находить значения тригонометрических функций по
заданному значению при различных способах задания функции,
применяя формулы тригонометрии, выполнять преобразования
1
3
78
1
3
79
1
3
80
1
3
81
1
3
82
1
3
83
1
3
84
1
3
85
выражений, решать простейшие тригонометрические уравнения и
неравенства.
Внеаудиторная самостоятельная работа:
1. «Об истории тригонометрии» - сообщение
2. «Роль Л. Эйлера в развитии тригонометрии» - доклад
3. «Доказательство тригонометрических тождеств» - изучение материала в
папке «Учись учиться»
4. «Решение простейших тригонометрических уравнений» - работа с папкой
«Учись учиться»
5. «Решение простейших тригонометрических неравенств» - работа с папкой
«Учись учиться»
6. «Примеры решения простейших тригонометрических неравенств» - конспект
по учебнику
7. «Формулы решения простейших тригонометрических уравнений» составление опорного конспекта
8. «Основы тригонометрии» - домашняя контрольная работа.
9. «Основные формулы тригонометрии» - составление справочника.
12
Второй семестр
Содержание учебного материала.
Тема 2.4.
Функции, их
свойства и
графики.
2.4.1.
2.4.2.
2.4.3.
Функции и способы их задания. Графики функций.
Определение числовой функции. Область определения функции.
Область значений функции. Способы задания функции (аналитический,
табличный, графический). Графики функций.
Четные и нечетные функции.
Определение четной функции, графическая иллюстрация. Определение
нечетной функции, графическая иллюстрация. Свойства четной и
нечетной функций.
Периодичность функций.
Определение периодической функции. Наименьший положительный
период у синуса, косинуса, тангенса и котангенса. Построение графиков
12
1
3
86
1
3
87
1
3
88
2.4.4.
2.4.5.
2.4.6.
2.4.7.
2.4.8.
2.4.9.
2.4.10.
2.4.11.
периодических функций.
Возрастание и убывание функции.
Определение возрастающей и убывающей функций. Нахождение
промежутков возрастания и убывания для четных и нечетных функций.
Экстремумы.
Определение точки максимума. Определение точки минимума.
Графическая иллюстрация точек экстремума. Экстремумы функции.
Схема исследования функции.
Область определения функции. Четность, нечетность функции.
Периодичность. Координаты точек пересечения графика с осями
координат. Промежутки, на которых функция принимает
положительные и отрицательные значения. Промежутки
монотонности. Точки экстремума и значения функции в этих точках.
Исследование функции.
Схема исследования функции. «Чтение» графиков. Построение
графиков в ходе экспериментальных исследований.
Решение задач.
Построение графиков. Исследование функции: область определения,
область значения; промежутки, на которых функция принимает
положительные и отрицательные значения и промежутки
монотонности. Экстремумы и точки экстремума.
Преобразование графиков.
Параллельный перенос вдоль оси ординат. Параллельный перенос
вдоль оси абсцисс. Растяжение и сжатие графика вдоль осей координат.
Обратные функции.
Обратимые функции. Взаимно обратные функции. Монотонная
функция является обратимой. Симметричность графиков .
Арифметические операции над функциями. Функциональная
зависимость. Независимая переменная. Функция, зависимая
переменная. Область определения и область значений функции.
Арифметические операции над функциями.
1
3
89
1
3
90
1
3
91
1
3
92
1
3
93
1
3
94
1
3
95
1
3
96
2.4.12.
Тема 2.5.
Степенная,
показательная и
тригонометрические
функции.
Сложная функция. Понятие сложной функции. Область определения
сложной функции. Внутренняя и внешняя функции.
1
3
97
Внеаудиторная самостоятельная работа:
1. Исследование функции – составление схемы.
2. «Способы задания функции» - составление конспекта.
3. «Обратная пропорциональность» - исследование функции.
4. «Квадратичная функция» - исследование функции.
5. «Приборы- самописцы построения графиков функций» - осциллограф,
кардиограф – доклад.
6. «Задачи в профессии сварщика, связанные с понятием функции» - сообщение.
7. «Задачи на ЕГЭ, связанные с чтением исследованием функции» - сообщение.
8. Преобразование графиков функций (параллельный перенос по осям
координат) – работа с папкой «Учись учиться».
9. Преобразование графиков функций (сжатие и растяжение по осям координат)
– работа с папкой «Учись учиться».
10. Домашняя контрольная работа по теме : «Функции и способы их задания».
12
Содержание учебного материала.
10
1
3
98
1
3
99
1
3
100
1
3
101
1
3
102
2.5.1.
2.5.2.
2.5.3.
2.5.4.
2.5.5.
Степенная функция. Свойства степенной функции. Определение
степенной функции. Исследование степенной функции. Графики
степенной функции.
Показательная функция.
Определение показательной функции. Свойства показательной
функции. Графики показательной функции. Монотонность.
Свойства и график показательной функции.
Исследование показательной функции на область определения,
область значений, монотонность. Построение графиков.
Свойства и график логарифмической функции.
Исследование логарифмической функции на область определения,
область значений, монотонность. Построение графиков.
Свойства функции y = sinx и ее график.
Область определения. Область значений. Четность и нечетность.
Наименьший положительный период. Координаты точек пересечения
графика с осями координат. Промежутки, на которых функция
принимает положительные и отрицательные значения. Промежутки
монотонности. Экстремумы функции и точки экстремума.
2.5.6.
Свойства функции y = cosx и ее график.
Область определения. Область значений. Четность и нечетность.
Наименьший положительный период. Координаты точек пересечения
графика с осями координат. Промежутки, на которых функция
принимает положительные и отрицательные значения. Промежутки
монотонности. Экстремумы функции и точки экстремума.
2.5.7.
Свойства функции y = tgx и ее график.
Область определения. Область значений. Четность и нечетность.
Наименьший положительный период. Промежутки, на которых
функция принимает положительные и отрицательные значения
Промежутки, на которых функция принимает положительные и
отрицательные значения. Промежутки монотонности. Экстремумы
функции и точки экстремума.
2.5.8.
Обратные тригонометрические функции.
Арксинус. Арккосинус. Арктангенс. Область определения.
Монотонность. Четность и нечетность.
2.5.9.
Решение задач.
Построение графиков степенной, показательной, логарифмической
функций. Исследование свойств.
2.5.10.
Контрольная работа №5.
Готовность определять основные свойства числовых функций,
иллюстрировать их на графиках, строить графики изученных функций,
иллюстрировать по графику свойства функций, использовать
графический метод решения уравнений.
Внеаудиторная самостоятельная работа:
1.Функция y = sinx и ее свойства – составление опорного конспекта по учебнику.
1
3
103
1
3
104
1
3
105
1
3
106
1
3
107
7
2. Функция y = cosx и ее свойства – составление опорного конспекта по учебнику.
3. Функция y = tgx и ее свойства – составление опорного конспекта по учебнику.
4. Обратные тригонометрические функции – составление таблицы с графиками и их
свойствами.
5. Преобразование графиков тригонометрических функций (параллельный перенос
по осям координат) - работа с папкой «Учись учиться».
6. Преобразование графиков тригонометрических функций (сжатие и растяжение) –
работа с папкой « Учись учиться».
Тема 2.6.
Уравнения и
неравенства.
Содержание учебного материала.
2.6.1.
2.6.2.
2.6.3.
2.6.4.
2.6.5.
Рациональные уравнения.
Понятие рационального уравнения. Область определения уравнения.
Целые уравнения. Дробные уравнения. Линейные и квадратные
уравнения. Алгоритм решения рационального уравнения.
Иррациональные уравнения.
Определение иррационального уравнения. Два метода решения
иррациональных уравнений: метод возведения обеих частей уравнения
в одну и ту же степень и метод введения новых переменных. Область
определения иррациональных уравнений.
Показательные уравнения. Понятие показательного уравнения. Три
основных метода решения показательных уравнений. 1)метод
уравнивания показателей, 2)метод ведения новой переменной,
3)вынесение за скобу.
Показательные уравнения, сводимые к квадратным уравнениям.
Понятие показательного уравнения. Метод замены переменной.
Область определения и область значений показательной функции.
Системы показательных уравнений.
Решение системы. Аналитический способ решения системы уравнений.
Метод подстановки. Метод сложения. Графический способ решения
систем уравнений.
28
1
3
108
1
3
109
1
3
110
1
3
111
1
3
112
2.6.6.
2.6.7.
2.6.8.
2.6.9.
2.6.10.
2.6.11.
2.6.12.
2.6.13.
Логарифмические уравнения.
Понятие логарифмического уравнения. Область определения
уравнения. Типы простейших логарифмических уравнений.
Равносильные уравнения. Потенцирование уравнений.
Методы решения логарифмических уравнений.
По определению логарифма – основной метод решения
логарифмических уравнений. Замена переменной. Потенцирование
уравнений.
Системы логарифмических уравнений.
Решение системы. Область определения системы логарифмических
уравнений. Аналитический способ решения системы логарифмических
уравнений. Метод подстановки. Метод сложения.
Тригонометрические уравнения.
Формулы решения простейших тригонометрических уравнений.
Частные случаи. Методы решения тригонометрических уравнений:
1) метод разложения на множители, 2) метод введения новой
переменной.
Решение тригонометрических уравнений.
Формулы решения простейших тригонометрических уравнений.
Частные случаи. Тригонометрические уравнения, приводимые к
уравнениям от одной тригонометрической функции одной переменной.
Решение тригонометрических уравнений, приводимых к квадратным.
Формулы решения простейших тригонометрических уравнений.
Частные случаи. Замена переменной. Однородные квадратные
уравнения.
Системы тригонометрических уравнений.
Методы решения систем уравнений. Метод подстановки. Метод
алгебраического сложения.
Рациональные неравенства.
Решение неравенства. Равносильные неравенства. Линейные
неравенства с одной переменной. Дробно-линейные неравенства.
1
3
113
1
3
114
1
3
115
1
3
116
1
3
117
1
3
118
1
3
119
1
3
120
2.6.14.
2.6.15.
2.6.16.
2.6.17.
2.6.18.
2.6.19.
2.6.20.
2.6.21.
2.6.22.
2.6.23.
Неравенства второй степени.
Иррациональные неравенства.
Понятие иррационально неравенства. Равносильные неравенства.
Область допустимых значений неравенства. Возведение обеих частей
неравенства в квадрат.
Показательные неравенства.
Свойства показательной функции. Монотонность. Область
определения. Область значений. Свойства степеней.
Примеры решения показательных неравенств.
Решение показательных неравенств на основании свойств
показательной функции и свойств степени.
Логарифмические неравенства.
Свойства логарифмической функции: область определения, область
значений. Возрастание и убывание. Свойства логарифмов.
Решение задач.
Решение рациональных неравенств. Метод интервалов. Решение
показательных неравенств. Решение логарифмических неравенств.
Тригонометрические неравенства.
Тригонометрическая окружность. Определение синуса, косинуса.
Примеры решения тригонометрических неравенств.
Решение тригонометрических неравенств.
Тригонометрическая окружность. Определение синуса, косинуса.
Решение тригонометрических неравенств с синусом, косинусом.
Исследование свойств и графиков функций при решении уравнений.
Графический метод решения уравнений. Графики функций. Абсциссы
точек пересечения построенных графиков. Функциональный метод
решения уравнений.
Исследование свойств и графиков функций при решении неравенств.
Графический метод решения неравенств. Графики функций.
Функциональный метод решения неравенств.
Метод интервалов.
1
3
121
1
3
122
1
3
123
1
3
124
1
3
125
1
3
126
1
3
127
1
3
128
1
3
129
1
3
130
Метод промежутков. Непрерывная функция. Алгоритм метода
интервалов: область определения, нули функции, интервалы, на
которых функция принимает положительные и отрицательные
значения.
2.6.24.
Решение задач.
Графический метод решения уравнений. Решение неравенств методом
интервалов. Алгоритм метода интервалов.
2.6.25.
Системы неравенств.
Решение системы неравенств. Запись в виде двойного неравенства.
Равносильные неравенства. Координатная прямая. Множество
решений системы неравенств.
2.6.26.
Способы решения систем неравенств.
Решение системы неравенств. Пересечение множеств решений
неравенств. Пересечение заштрихованных промежутков. Свойства
неравенств. Изменение знака неравенства.
2.6.27.
Решение задач.
Решение систем неравенств. Свойства неравенств. Изменение знака
неравенства. Координатная прямая, пересечение заштрихованных
промежутков.
2.6.28.
Контрольная работа №6.
Умение решать рациональные, показательные, логарифмические,
тригонометрические уравнения, приводимые к линейным и
квадратным, а так же аналогичные неравенства и системы неравенств.
Внеаудиторная самостоятельная работа:
1.Рациональные уравнения – тренировочная работа.
2.Иррациональные уравнения - работа с папкой «Учись учиться».
3. Показательные уравнения - работа с папкой «Учись учиться».
4. Логарифмические уравнения – работа с методическим пособием
«Логарифмические уравнения».
5.Тригонометрические уравнения – работа с методическим пособием по решению
уравнений.
1
3
131
1
3
132
1
3
133
1
3
134
1
3
135
22
6.Квадратные и однородные тригонометрические уравнения – домашняя
контрольная работа.
7.Рациональные неравенства – тренировочная работа.
8.Иррациональные неравенства - работа с папкой «Учись учиться».
9.Показательные неравенства – составление схемы решения показательных
неравенств.
10. Логарифмические неравенства – составление схемы решения логарифмические
неравенств.
11.Тригонометрические неравенства - работа с папкой «Учись учиться».
12.Решение тригонометрических неравенств – работа по учебнику, составление
конспекта.
13.Исследование свойств и графиков функций при решении уравнений – работа с
папкой «Учись учиться».
14. .Исследование свойств и графиков функций при решении неравенств– работа с
папкой «Учись учиться».
15.Метод интервалов – работа по составлению алгоритма метода интервалов.
16.Уравнения и неравенства – домашняя контрольная работа.
17. Исследование уравнений и неравенств с модулем – сообщение.
18. Исследование уравнений и неравенств с параметром – работа с пособием.
Раздел 3 Начала математического анализа.
Тема 3.1.
Содержание учебного материала.
Начала
3.1.1.
Последовательности.
математичесЧисловые последовательности. Общий член последовательности.
Монотонные последовательности. Ограниченные последовательности.
кого анализа.
3.1.2.
3.1.3.
Сумма бесконечно убывающей геометрической прогрессии.
Определение геометрической прогрессии. Общий член геометрической
прогрессии. Сумма первых n членов геометрической прогрессии.
Бесконечно убывающая геометрическая прогрессия.
Понятие о непрерывности функции.
34
34
1
3
136
1
3
137
1
3
138
3.1.4.
3.1.5.
3.1.6.
3.1.7.
3.1.8.
3.1.9.
3.1.10.
3.1.11.
Область определения функции. Приращение аргумента. Приращение
функции. Графическая иллюстрация. Определение непрерывной
функции. Точки разрыва функции.
Понятие о производной.
Задача о скорости движущейся точки. Средняя скорость. Мгновенная
скорость. Задача о касательной к данной кривой. Графическая
иллюстрация. Определение производной.
Производная суммы, произведения и частного.
Правила дифференцирования суммы, произведения и частного.
Примеры.
Правила дифференцирования.
Производная степенной функции. Производная суммы. Производная
произведения. Производная частного. Таблица производных.
Решение задач.
Решение задач на применение производной степенной функции, правил
дифференцирования.
Производные основных элементарных функций.
Производные степенной, показательной, логарифмической,
тригонометрической функций. Практические задачи на применение
производных комбинированных функций.
Производная сложной функции.
Понятие сложной функции. Правило дифференцирования производной
сложной функции. Примеры.
Геометрический смысл производной.
Прямая. Угловой коэффициент прямой. График функции. Касательная к
графику функции. Значение производной функции в заданной точке и
угловой коэффициент касательной в этой точке.
Уравнение касательной.
Алгоритм нахождения уравнения касательной к графику функции в
заданной точке. Нахождение производной. Вычисление производной в
заданной точке. Вычисление функции в заданной точке. Уравнение
1
3
139
1
3
140
1
3
141
1
3
142
1
3
143
1
3
144
1
3
145
1
3
146
3.1.12.
3.1.13.
3.1.14.
3.1.15.
3.1.16.
3.1.17.
касательной.
Признак возрастания (убывания) функции.
Значение производной в некотором промежутке. Угловой коэффициент
касательной. Признак возрастания (убывания) функции. Теорема о
достаточном условии возрастания функции. Промежутки монотонности
функции.
Применение признака возрастания (убывания) функции.
Решение задач на нахождение промежутков монотонности. Применение
достаточного признака возрастания (убывания) функции.
Экстремумы функции.
Определение точки максимума. Графическая интерпретация точки
максимума. Определение точки минимума. Графическая интерпретация
точки минимума. Определение точки экстремума. Теорема Ферма.
Критические точки функции.
Понятие критической точки функции. Алгоритм поиска критической точки
функции. Внутренняя точка области определения. Производная в
заданной точке равна 0. Производная в заданной точке не существует.
Применение производной к исследованию функции.
Область определения функции. Промежутки монотонности с помощью
производной. Точки экстремума. Таблица. График.
Решение задач.
Задачи на определение промежутков возрастания и убывания функции,
на нахождение точек максимума и минимума, точек экстремума и
экстремума функции, построение графика функции на основании
исследования.
1
3
147
1
3
148
1
3
149
1
3
150
1
3
151
1
3
152
3.1.18.
Контрольная работа №7.
Умение находить производные элементарных функций, применять
правила дифференцирования, находить производные сложных функций,
вычислять значения функции и её производной в указанных точках,
находить уравнение касательной, решать прикладные задачи на
нахождение скорости и ускорения.
1
3
153
3.1.19.
Построение графиков.
Исследование графиков функции с помощью производной. Таблица.
График.
Производная обратной функции.
Понятие обратной функции. Симметричность графиков прямой и
обратной функции относительно прямой у = х. произведение
производных в заданной точке взаимообратных функций равно единице.
Наибольшее и наименьшее значение функции.
Алгоритм нахождения наибольшего и наименьшего значения функции.
Критические точки функции, лежащие внутри промежутка. Значение
функции в этих точках и на концах промежутков. Выбор наибольшего и
наименьшего значения.
Решение прикладных задач.
Метод поиска наибольшего и наименьшего значения функции.
Схема:
1) задача «переводится» на язык функции;
2) средствами анализа ищется наибольшее или наименьшее значение
функции на промежутке;
3) выясняется, какой практический смысл (в терминах первоначальной
задачи) имеет полученный (на языке функции) результат.
Производная показательной функции.
Таблица производных. Правила дифференцирования. Производная
показательной простой и сложной функций.
Производная логарифмической функции.
1
3
154
1
3
155
1
3
156
1
3
157
1
3
158
1
3
159
3.1.20.
3.1.21.
3.1.22.
3.1.23.
3.1.24.
3.1.25.
3.1.26.
3.1.27.
3.1.28.
3.1.29.
3.1.30.
3.1.31.
3.1.32.
Таблица производных. Правила дифференцирования. Производная
логарифмической простой и сложной функций.
Решение задач.
Решение задач по алгоритму нахождения наибольшего и наименьшего
значений функции на отрезке. Задачи прикладного характера.
Определение первообразной.
Обратные операции. Дифференцирование. Интегрирование.
Определение первообразной.
Основное свойство первообразной.
Общий вид первообразных. Признак постоянства функции. Теорема.
Геометрический смысл основного свойства первообразных.
Три правила нахождения первообразных.
Таблица первообразных. Определение первообразной.
Неопределенный интеграл. Правила нахождения первообразных.
Решение задач.
Таблица первообразных. Нахождение первообразной, принимающей
заданное значение в указанной точке. Правила нахождения
первообразных.
Понятие интеграла.
Криволинейная трапеция. Теорема о площади криволинейной трапеции.
Непрерывная и неотрицательная на отрезке функция. Вычисление
площади криволинейной трапеции через сумму площадей
прямоугольников. Определённый интеграл функции.
Формула Ньютона- Лейбница.
Геометрический смысл формулы Ньютона- Лейбница. Площадь
криволинейной трапеции. Пределы интегрирования. Знак интеграла.
Подынтегральная функция. Переменная интегрирования. Таблица
первообразных.
Примеры применения интеграла в физике и технике.
Вычисление объемов тел. Объем усеченной пирамиды. Объем тел
вращения. Работа переменной силы.
1
3
160
1
3
161
1
3
162
1
3
163
1
3
164
1
3
165
1
3
166
1
3
167
3.1.33.
Решение задач.
Формула Ньютона- Лейбница. Решение задач на нахождение площади
криволинейной трапеции, ограниченной заданными линиями.
3.1.34.
Контрольная работа №8.
Умение находить производные элементарных функций, использовать
производную для изучения свойств функций, построения графиков,
решать задачи прикладного характера на нахождение наибольшего и
наименьшего значений, вычислять площади с использованием
определенного интеграла, решать прикладные задачи на нахождение
скорости и ускорения.
Внеаудиторная самостоятельная работа:
1. «Последовательности и их свойства» - составление конспекта по
учебнику.
2. «Сумма бесконечно убывающей геометрической прогрессии» работа с папкой «Учись учиться».
3. «Задачи о скорости движущейся точки» - составление опорного
конспекта.
4. «Задачи о касательной к данной кривой» - составление опорного
конспекта.
5. Таблица производных элементарных функций – составление
справочника.
6. Примеры производной сложной функции - домашняя тренировочная
работа.
7. Уравнение касательной – составление схемы написания уравнения
касательной.
8. Понятие дифференциала и его приложение – сообщение.
9. «Из истории дифференциального исчисления» - доклад.
10. Роль Р. Декарта в развитии математического анализа.
11. П.Ферма и его вклад в развитие математики – доклад.
12. Л.Эйлер и его вклад в развитие математики – доклад.
13. Достаточные условия возрастания и убывания функции – изучение по
1
3
168
1
3
169
32
учебнику.
14. Экстремумы функции – графическая интерпретация.
15. Критические точки функции – составление схемы.
16. Применение производной к исследованию функции – составление
алгоритма.
17. Задачи на нахождение промежутков возрастания – составление
алгоритма.
18. Задачи на нахождение критических точек – составление алгоритма.
19. Производная обратной функции – составление таблицы.
20. Наибольшее и наименьшее значение функции - составление
алгоритма.
21. Решение прикладных задач на нахождение наибольшего и
наименьшего значений функции - домашняя тренировочная работа.
22. Таблица первообразных – составление конспекта.
23. Основное свойство первообразных – графическая иллюстрация на
примерах.
24. Роль Лейбница в развитии математического анализа – сообщение.
25. Роль Ньютона а в развитии математического анализа – сообщение.
26. К.Гаусс и его вклад в развитие математики – доклад.
27. «Производная в экономике» - сообщение.
28. «Производная в медицине и химии» - сообщение.
29. «Производная в физике» - сообщение.
30. «Производная в технике» - сообщение.
31. «Интеграл в физике и технике» - доклад.
32. «Интеграл в геометрии» - доклад.
33. Примеры криволинейных трапеций - работа с папкой «Учись
учиться».
34. Вычисление площадей криволинейных трапеций - работа с папкой
«Учись учиться».
Раздел 4
Геометрия.
Содержание учебного материала.
Тема 4.1.
4.1.1.
Прямые и
плоскости в
пространстве.
4.1.2.
4.1.3.
4.1.4.
4.1.5.
4.1.6.
4.1.7.
Повторение курса планиметрии.
Равнобедренный треугольник. Прямоугольный треугольник.
Соотношения между сторонами и углами в прямоугольном
треугольнике. Признаки равенства треугольников.
Аксиомы стереометрии. Некоторые следствия из аксиом.
Основные понятия планиметрии. Основные понятия стереометрии.
Принадлежность. Множество. Аксиомы, характеризующие взаимное
расположение точек, прямых и плоскостей. Профессиональная
направленность аксиом стереометрии.
Параллельные прямые в пространстве. Признак параллельности в
пространстве.
Определение параллельных прямых. Теорема о параллельности трех
прямых. Признак параллельности прямых.
Параллельность прямой и плоскости.
Три случая взаимного расположения прямой и плоскости в
пространстве. Определение параллельности прямой и плоскости.
Признак параллельности прямой и плоскости.
Свойства параллельности прямой и плоскости.
Определение параллельности прямой и плоскости. Свойства
параллельности прямой и плоскости.
Скрещивающиеся прямые. Угол между прямыми.
Три случая взаимного расположения двух прямых в пространстве.
Понятие скрещивающихся прямых. Наглядное представление о
скрещивающихся прямых. Угол между пересекающимися прямыми.
Угол между скрещивающимися прямыми.
Параллельные плоскости.
Определение параллельности плоскостей. Признак параллельности
77
19
1
3
170
1
3
171
1
3
172
1
3
173
1
3
174
1
3
175
1
3
176
4.1.8.
4.1.9.
4.1.10.
4.1.11.
4.1.12.
4.1.13.
4.1.14.
4.1.15.
плоскостей.
Решение задач.
Решение задач на применение свойств параллельных плоскостей.
Пересечение параллельных плоскостей третьей плоскостью. Отрезки
параллельных прямых, заключенные между параллельными
плоскостями.
Перпендикулярные прямые в пространстве.
Определение перпендикулярных прямых в пространстве. Лемма о
перпендикулярности двух параллельных прямых к третьей прямой.
Перпендикулярная прямая и плоскость.
Взаимно перпендикулярные прямые. Понятие прямой
перпендикулярной к плоскости. Примеры из жизни. Теоремы,
устанавливающие связь между параллельностью прямых и их
перпендикулярностью к плоскости.
Расстояние от точки до плоскости.
Понятие перпендикуляра к плоскости. Основание перпендикуляра.
Наклонная. Проекция наклонной на плоскость. Сравнение длины
перпендикуляра, проведенного из данной точки к плоскости и длины
любой наклонной, проведенной из той же точки к плоскости. Примеры
из жизни.
Решение задач.
Решение задач на нахождение расстояния от точки до плоскости.
Решение задач на нахождение расстояния от точки к прямой.
Теорема о трех перпендикулярах.
Перпендикуляр к плоскости. Наклонная. Проекция наклонной. Теорема
о трех перпендикулярах (прямая и обратная).
Угол между прямой и плоскостью.
Проекция точки на плоскость. Проекция прямой на плоскость,
перпендикулярную этой прямой. Угол между прямой и плоскостью.
Двугранный угол.
Понятие угла в планиметрии. Плоскость. Полуплоскости. Грани. Общая
1
3
177
1
3
178
1
3
179
1
3
180
1
3
181
1
3
182
1
3
183
1
3
184
граница полуплоскостей. Ребро двугранного угла. Иллюстрации
двугранного угла в жизни. Линейный угол двугранного угла. Прямой,
острый, тупой двугранный угол.
4.1.16.
Признак перпендикулярности двух плоскостей.
Угол между пересекающимися плоскостями. Взаимно
перпендикулярные плоскости. Иллюстрации взаимно
перпендикулярных плоскостей. Профессиональная направленность.
Признак перпендикулярности двух плоскостей.
4.1.17.
Параллельное проектирование. Изображение пространственных
фигур.
Проекция прямой. Проекция отрезка. Проекции параллельных
отрезков, а так же проекции параллельных отрезков, лежащих на
одной прямой. Проекция середины отрезка. Свойства параллельного
проектирования. Тетраэдр. Штриховые линии. Параллелепипед.
Прямоугольная проекция в техническом изучении. Проекция
цилиндрической втулки.
4.1.18.
Решение задач.
Решение задач на нахождение угла между прямой и плоскостью,
линейного угла. Задачи на применение признака перпендикулярности
двух плоскостей.
4.1.19.
Контрольная работа№9.
Умение описывать взаимное расположение прямых и плоскостей в
пространстве. Применение определений, признаков параллельности и
перпендикулярности прямой и плоскости. Умение решать простейшие
планиметрические и стереометрические задачи.
Внеаудиторная самостоятельная работа:
1. Признаки равенства треугольников – составление схемы.
2. Соотношение между сторонами и углами в прямоугольном треугольнике –
составление справочника.
3. Аксиомы стереометрии – составление опорного конспекта.
4. Случаи взаимного расположения прямой и плоскости в пространстве –
1
3
185
1
3
186
1
3
187
1
3
188
10
иллюстрация на рисунках.
5. Примеры взаимного расположения прямых в пространстве - иллюстрация на
рисунках.
6. «Перпендикулярность прямых и плоскостей в жизни и моей профессии» сообщение.
7. «Параллельность прямых и плоскостей в жизни и моей профессии» сообщение.
8. Изготовление модели тетраэдра.
9. Изготовление модели параллелепипеда.
10. «Расстояние от точки до плоскости» - составление опорного конспекта.
11. «Параллельное проектирование» - доклад.
12. «Изображение пространственных фигур» - составление схемы.
13. «Проекции цилиндрической втулки» - составление чертежа.
Тема 4.2.
Содержание учебного материала
Понятие вектора. Сложение и вычитание векторов.
Координаты и 4.2.1.
Определение вектора. Нулевой вектор. Длина вектора.
векторы.
4.2.2.
4.2.3.
4.2.4.
4.2.5.
4.2.6.
Сонаправленные вектора. Противоположно направленные вектора.
Равные вектора. Сложение и вычитание векторов.
Умножение вектора на число.
Ненулевой вектор. Длина вектора. Сонаправленные вектора.
Противоположно направленные вектора. Коллинеарные вектора.
Компланарные вектора.
Определение компланарных векторов. Параллелепипед. Разложение
компланарных векторов.
Разложение вектора.
Теорема о разложении вектора по трем некомпланарным векторам.
Коэффициенты разложения. Определение некомпланарных векторов.
Прямоугольная система координат в пространстве.
Оси координат. Начало координат. Координатные плоскости. Абсцисса,
ордината, аппликата. Координаты точки.
Координаты вектора.
12
1
3
189
1
3
190
1
3
191
1
3
192
1
3
193
1
3
194
4.2.7.
4.2.8.
4.2.9.
4.2.10.
4.2.11.
4.2.12.
Прямоугольная система координат в пространстве. Единичный вектор.
Координаты вектора. Некомпланарные векторы. Разложение вектора
по координатам векторов. Координаты равных векторов. Действия над
векторами в координатной форме.
Связь между координатами векторов и координатами точек.
Радиус вектор данной точки. Определение координат любой точки
через соответствующие координаты ее радиус – вектора. Определение
координат вектора как разности соответствующих координат его конца
и начала.
Простейшие задачи в координатах.
Координаты середины отрезка. Длина вектора по его координатам.
Расстояние между двумя точками.
Угол между векторами.
Определение угла между векторами. Нулевой угол сонаправленных
векторов. Перпендикулярные вектора.
Скалярное произведение векторов.
Определение скалярного произведения векторов. Необходимое и
достаточное условие перпендикулярности двух векторов. Определение
скалярного квадрата вектора через квадрат его длины.
Решение задач.
Решение задач на применение необходимого и достаточного условия
перпендикулярности двух векторов. Простейшие задачи в координатах.
Контрольная работа №10.
Умение распознавать на чертежах и моделях пространственные формы,
соотносить трехмерные объекты с их изображением, решать
планиметрические, стереометрические простейшие задачи в
координатной и векторной форме.
Внеаудиторная самостоятельная работа:
1. Действия над векторами – составление опорного конспекта.
1
3
195
1
3
196
1
3
197
1
3
198
1
3
199
1
3
200
6
2. Прямоугольная система координат в пространстве - составление опорного
конспекта.
3. «Изображение точек в декартовой прямоугольной системе координат» построение точек.
4. Декартовая прямоугольная система координат - работа с папкой «Учись
учиться».
5. Простейшие задачи в координатах - домашняя тренировочная работа.
Тема 4.3.
Содержание учебного материала.
Понятие многогранника.
Многогранни 4.3.1.
Тетраэдр. Параллелепипед. Грани. Ребра. Вершины. Диагональ.
ки.
4.3.2.
4.3.3.
4.3.4.
4.3.5.
4.3.6.
4.3.7.
Секущая плоскость. Выпуклые и невыпуклые многогранники.
Многогранные углы.
Двугранный угол. Грани. Ребро. Мера двугранного угла. Трехгранный
угол. Многогранный угол.
Теорема Эйлера.
Выпуклый многогранник. Вершины. Грани. Теорема Эйлера.
Иллюстрация на многограннике.
Призма.
Основание, боковые грани, боковые ребра. Высота призмы.
Правильная призма. Площадь боковой поверхности призмы. Площадь
полной поверхности призмы.
Прямоугольный параллелепипед.
Вершины. Грани. Ребра параллелепипеда. Диагональ
параллелепипеда. Основания, боковые грани параллелепипеда.
Свойства параллелепипеда.
Симметрия в пространстве.
Симметрия в планиметрии относительно точки и прямой. В
стереометрии симметрия относительно точки прямой, плоскости.
Понятие центра, оси, плоскости симметрии фигуры. Симметрия в
природе, архитектуре, технике, быту.
Симметрии в кубе и параллелепипеде.
14
1
3
201
1
3
202
1
3
203
1
3
204
1
3
205
1
3
206
1
3
207
4.3.8.
4.3.9.
4.3.10.
4.3.11.
4.3.12.
4.3.13.
4.3.14.
Симметрия относительно центра симметрии. Симметрия
относительно оси. Симметрия относительно плоскости. Куб.
Параллелепипед.
Сечение призмы.
Призма. Свойство параллельности линий пересечения двух
параллельных плоскостей третьей. Секущая плоскость.
Пирамида.
Понятие пирамиды. Основание. Боковые грани, вершина, боковые
ребра, высота пирамиды. Площадь полной поверхности пирамиды.
Площадь боковой поверхности пирамиды.
Правильная пирамида.
Понятие правильной пирамиды. Боковые грани, боковые ребра.
Апофема. Площадь боковой поверхности правильной пирамиды.
Усеченная пирамида.
Понятие усеченной пирамиды. Нижние и верхние основания. Боковые
ребра, высота. Боковые грани. Правильная усеченная пирамида.
Площадь боковой поверхности правильной усеченной пирамиды.
Сечения пирамиды.
Пирамида. Свойство параллельности линий пересечения двух
параллельных плоскостей третьей. Секущая плоскость.
Правильный многогранник.
Понятие правильного многогранника. Правильный тетраэдр.
Правильный октаэдр. Куб. Правильный икосаэдр. Правильный
додекаэдр.
Решение задач.
Решение задач на нахождение основных элементов правильной
пирамиды и правильных многогранников. Нахождение полной и
боковой поверхности правильной пирамиды.
Внеаудиторная самостоятельная работа:
1. Л.Эйлер и его вклад в развитие геометрии – сообщение
1
3
208
1
3
209
1
3
210
1
3
211
1
3
212
1
3
213
1
3
214
6
2. Параллелепипед, куб, тетраэдр, октаэдр, икосаэдр, додекаэдр – изготовление
моделей геометрических фигур.
Тема 4.4.
Тела
вращения.
Содержание учебного материала
4.4.1.
4.4.2.
4.4.3.
4.4.4.
4.4.5.
4.4.6.
4.4.7.
4.4.8.
4.4.9.
Понятие цилиндра.
Основание цилиндра. Образующие цилиндра. Радиус и высота. Ось
цилиндра. Боковая поверхность цилиндра.
Решение задач.
Задачи на нахождение основных элементов цилиндра. Вычисление
боковой поверхности цилиндра.
Сечение цилиндра.
Понятие цилиндра. Ось цилиндра. Осевое сечение цилиндра. Сечение,
параллельное оси цилиндра. Сечение, перпендикулярное оси
цилиндра.
Решение задач.
Задачи на нахождение площади осевого сечения цилиндра. Задачи на
нахождение площади сечения перпендикулярного оси.
Понятие конуса.
Основание конуса. Вершина конуса. Образующие конуса. Ось конуса.
Высота конуса. Боковая поверхность конуса.
Сечение конуса.
Понятие конуса. Ось конуса. Осевое сечение конуса. Сечение конуса,
проходящее через вершину и хорду. Сечение перпендикулярное оси
конуса.
Решение задач.
Задачи на нахождение площади осевого сечения конуса. Задачи на
нахождение площади сечения перпендикулярного оси.
Усеченный конус.
Понятие усеченного конуса. Основания конуса. Высота. Образующие.
Боковая поверхность усеченного конуса.
Решение задач.
15
1
3
215
1
3
216
1
3
217
1
3
218
1
3
219
1
3
220
1
3
221
1
3
222
1
3
223
4.4.10.
4.4.11.
4.4.12.
4.4.13.
4.4.14.
Задачи на нахождение боковой поверхности усеченного конуса.
Задачи с профессиональной направленностью.
Сфера и шар.
Определение сферы и шара. Радиус сферы. Диаметр сферы. Центр,
радиус и диаметр шара. Вращение полуокружности вокруг диаметра.
Решение задач.
Задачи на нахождение основных элементов сферы и шара.
Нахождение площади сферы.
Взаимное расположение сферы и плоскости.
Расстояние от центра сферы до плоскости меньше радиуса сферы.
Сечение шара плоскостью. Больший круг шара. Расстояние от центра
сферы до плоскости равно радиусу сферы. Расстояние от центра сферы
до плоскости больше радиуса сферы.
Касательная плоскость к сфере.
Касательная плоскость. Точка касания. Теорема о касательной
плоскость к сфере.
Решение задач.
Задачи на нахождение расстояния от центра шара до секущей
плоскости. Задачи на вычисление площади сферы.
Дифференцированный зачет (Контрольная работа№11).
Умение изображать основные многогранники, тела вращения,
выполнять чертежи по условию задачи, решать стереометрические
простейшие задачи, используя планиметрические факты и методы.
Внеаудиторная самостоятельная работа:
1. Тела вращения – справочник формул вычисления полной и боковой
поверхности.
2. Модели тел вращения – изготовление моделей геометрических фигур.
1
3
224
1
3
225
1
3
226
1
3
227
1
3
228
1
3
229
4.4.15.
ТРЕТИЙ
СЕМЕСТР
4
Тема 4.5.
Измерения в
геометрии.
Содержание учебного материала.
4.5.1.
4.5.2.
4.5.3.
4.5.4.
4.5.5.
4.5.6.
4.5.7.
Понятие объема. Интегральная форма объема.
Единица измерения объема. Куб. Кубический сантиметр. Кубический
метр. Кубический миллиметр. Свойства объемов. Равные тела, равные
объемы. Объем тела, составленного из нескольких тел. Сумма
объемов.
Объем призмы.
Призма. Площадь основания. Высота. Объем прямой призмы. Теорема
о вычислении объема прямой призмы.
Объем пирамиды.
Пирамида. Площадь основания. Высота. Объем пирамиды. Теорема о
вычислении объема пирамиды. Следствие из теоремы о вычислении
объема усеченной пирамиды.
Решение задач.
Задачи на нахождение объема прямой призмы. Нахождение объема
пирамиды.
Площадь поверхности призмы.
Призма. Высота призмы. Площадь полной поверхности призмы.
Площадь боковой поверхности призмы. Периметр основания.
Площадь поверхности пирамиды.
Пирамида. Боковые грани, боковые ребра, высота пирамиды. Сумма
площадей всех граней. Площадь полной поверхности пирамиды.
Сумма площадей боковых граней пирамиды. Площадь боковой
поверхности пирамиды.
Подобие многогранников.
Пирамида. Секущая плоскость параллельная основанию.
Преобразование подобия – гомотетия. Линейные размеры. Площади
17
1
3
230
1
3
231
1
3
232
1
3
233
1
3
234
1
3
235
1
3
236
4.5.8.
4.5.9.
4.5.10.
4.5.11.
4.5.12.
4.5.13.
4.5.14.
4.5.15.
4.5.16.
подобных фигур.
Решение задач.
Задачи на нахождение площади боковой поверхности призмы,
площади боковой поверхности пирамиды. Задачи на нахождение
площади полной поверхности призмы, площади полной поверхности
пирамиды.
Объем цилиндра.
Понятие цилиндра. Высота. Площадь основания. Теорема об объеме
цилиндра.
Объем конуса.
Понятие конуса. Высота. Площадь основания. Теорема об объеме
конуса. Следствие: объем усеченного конуса.
Объем шара.
Понятие шара. Радиус шара. Объем шара. Объемы шарового сегмента,
шарового слоя и шарового сектора.
Решение задач.
Задачи на нахождение объема цилиндра, объема конуса, объема
шара.
Площадь поверхности цилиндра.
Развертка боковой поверхности цилиндра. Площадь боковой
поверхности цилиндра. Длина окружности основания. Высота
цилиндра. Площадь поверхности цилиндра.
Площадь поверхности конуса.
Развертка боковой поверхности конуса. Круговой сектор. Радиус
сектора. Образующая конуса. Площадь развертки. Площадь боковой
поверхности конуса. Площадь полной поверхности конуса.
Площадь сферы.
Описанный около сферы многогранник. Последовательность
описанных около сферы многогранников. Площадь сферы как предел
последовательности площадей поверхностей этих многогранников.
Решение задач.
1
3
237
1
3
238
1
3
239
1
3
240
1
3
241
1
3
242
1
3
243
1
3
244
1
3
245
4.5.17.
Задачи на вычисление площади боковой поверхности цилиндра,
боковой поверхности конуса. Задачи на вычисление площади
поверхности цилиндра, площади поверхности конуса.
Контрольная работа №12.
Умение распознавать на чертежах и моделях пространственные
формы; изображать основные многогранники и круглые тела;
выполнять чертежи по условиям задач; решать стереометрические
задачи на нахождение площадей и объёмов, используя
планиметрические факты и методы.
Внеаудиторная самостоятельная работа:
1
3
246
1
3
247
1
3
248
1
3
249
1
3
250
1
3
251
2
«Геометрия в моей профессии» - сообщения обучающихся.
Третий семестр.
Раздел 5 Элементы комбинаторики и теории вероятностей.
Содержание учебного материала.
5.1.1.
Тема 5.1.
Элементы
комбинатори 5.1.2.
ки.
5.1.3.
5.1.4.
5.1.5.
Основные элементы комбинаторики.
Группы, составленные из каких-либо элементов. Задачи на подсчет
различных соединений. Комбинаторные задачи.
Правило произведения.
Варианты выбора первого элемента. Варианты выбора второго
элемента. Привило произведения.
Задачи на подсчет числа размещений.
Понятие размещений.
Формула для вычисления числа размещений.
Задачи на подсчет числа перестановок.
Понятие перестановок.
Формула для вычисления числа перестановок.
Задачи на подсчет числа сочетаний.
Понятие сочетаний.
22
11
5.1.6.
5.1.7
5.1.8
5.1.9
5.1.10
5.1.11
Формула для вычисления числа сочетаний.
Решение задач.
Задачи на подсчет числа размещений, перестановок, сочетаний.
Выбор нескольких вариантов.
Формула для подсчета числа сочетаний. Формула для подсчета числа
размещений и перестановок.
Решение задач на перебор вариантов.
Задачи на подсчет числа размещений, перестановок, сочетаний.
Формула бинома Ньютона. Треугольник Паскаля.
Бином Ньютона, биноминальные коэффициенты. Треугольник
Паскаля.
Комбинаторные задачи.
Правило произведения. Размещения. Перестановки. Сочетания.
Решение задач.
Задачи на подсчет числа размещений и сочетаний.
Содержание учебного материала.
5.2.1
Тема 5.2.
Элементы
теории
вероятностей. 5.2.2
Элементы
математической
статистики. 5.2.3
5.2.4
События и их вероятности.
Определение события. Достоверные события. Невозможные события.
Несовместные события. Противоположные события. Вероятности
событий. Классическое определение вероятности.
Сложение и умножение вероятностей.
Вероятность события. Вероятность суммы двух несовместных событий.
Сумма вероятностей противоположных событий. Вероятность
произведения двух зависимых событий.
Понятие о независимом событии.
Независимые события.
Умножение вероятностей независимых событий.
Дискретная случайная величина.
Случайные величины. Анализ информации о различных случайных
величинах. Статистика. Статистическое определение вероятности.
1
3
252
1
3
253
1
3
254
1
3
255
1
3
256
1
3
257
1
3
258
1
3
259
1
3
260
1
3
261
11
5.2.5
5.2.6
5.2.7
5.2.8
5.2.9
5.2.10
5.2.11
Закон распределения случайных величин. Числовые характеристики
случайной величины.
Дискретные случайные величины. Непрерывные случайные величины.
Гистограмма частот.
Понятие о законе больших чисел.
Независимые испытания. Вероятность наступления события. Теорема
о законе больших чисел.
1
3
262
1
3
263
Представление данных.
Табличное представление данных. Графическое представление
данных.
Генеральная совокупность, выборка.
Однотипные объекты. Общие параметры. Репрезентативная выборка.
Среднее арифметическое, медиана.
Значение случайной величины. Упорядоченная выборка. Медиана.
Сумма всех чисел выборки. Среднее арифметическое.
1
3
264
1
3
265
1
3
266
Задачи математической статистики.
Мода. Медиана. Среднее арифметическое выборки.
Решение практических задач.
Нахождение медианы и среднего арифметического выборки.
1
3
267
1
3
268
4
1
3
269
1
3
270
Раздел 6 Повторение курса ОДБ.10 Математика
Тема 6.1.
Уравнения, 6.1.1
неравенства и
системы
6.1.2
уравнений.
Содержание учебного материала.
Логарифмические уравнения.
Область определения уравнения. Типы простейших логарифмических
уравнений. Равносильные уравнения.
Логарифмические неравенства.
Свойства логарифмической функции: область определения, область
значений, возрастание и убывание. Свойства логарифмов.
12
6.1.3
6.1.4
Тема 6.2.
Измерения в
геометрии.
6.5.1.
6.5.2.
6.5.3.
6.5.4.
6.5.5.
6.5.6.
6.5.7.
6.5.8.
Иррациональные уравнения.
Определение иррационального уравнения. Методы решений
иррациональных уравнений: метод возведения обеих частей
уравнения в одну и ту же степень. Метод введения новых
переменных. Область определения.
Системы уравнений.
Аналитический способ решения систем уравнений. Метод
подстановки. Метод сложения.
1
3
271
1
3
272
Содержание учебного материала.
8
Объем призмы.
Призма. Площадь основания. Высота. Объем прямой призмы.
Объем пирамиды.
Пирамида. Площадь основания. Теорема о вычислении объема
пирамиды.
Площадь поверхности призмы.
Призма. Высота призмы. Периметр основания. Площадь боковой
поверхности призмы. Площадь полной поверхности призмы.
Площадь поверхности пирамиды.
Пирамида. Площадь боковой поверхности пирамиды. Площадь
полной поверхности пирамиды.
Объем конуса.
Понятие конуса. Высота. Площадь основания. Теорема об объеме
конуса.
Объем цилиндра и шара.
Понятия цилиндра и шара. Высота цилиндра. Радиус цилиндра. Радиус
шара. Формулы объемов цилиндра и шара.
Площадь поверхности цилиндра и конуса.
Площадь боковой поверхности цилиндра и конуса. Площадь полной
поверхности цилиндра и конуса.
Дифференцированный зачёт. (Контрольная работа №13.)
Умение решать показательные, логарифмические,
1
3
273
1
3
274
1
3
275
1
3
276
1
3
277
1
3
278
1
3
279
1
3
280
тригонометрические уравнения, а так же аналогичные неравенства.
Умение обучающихся решать стереометрические задачи на
нахождение площадей и объемов, используя при решении
планиметрические факты и методы.